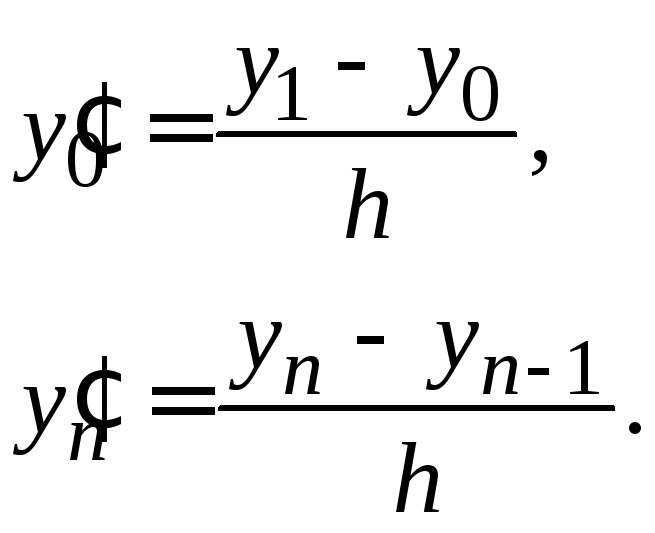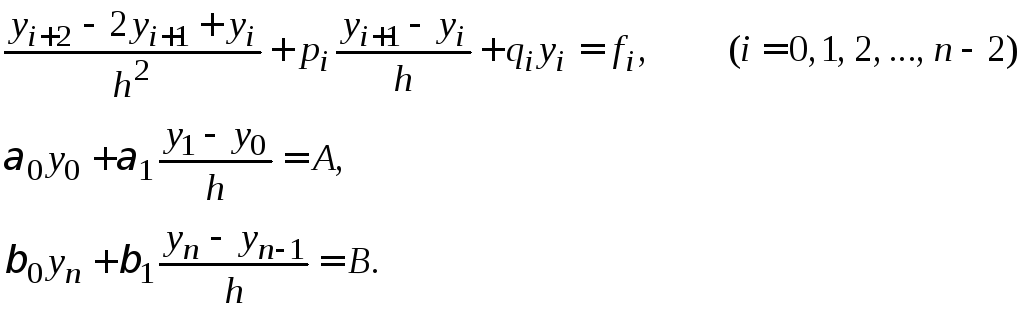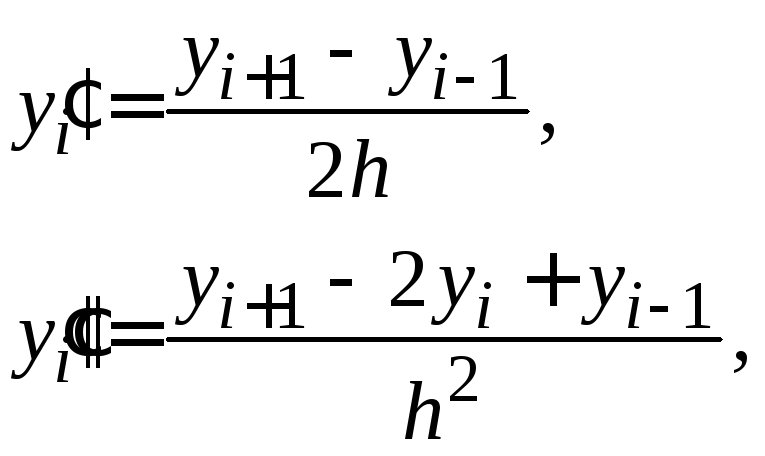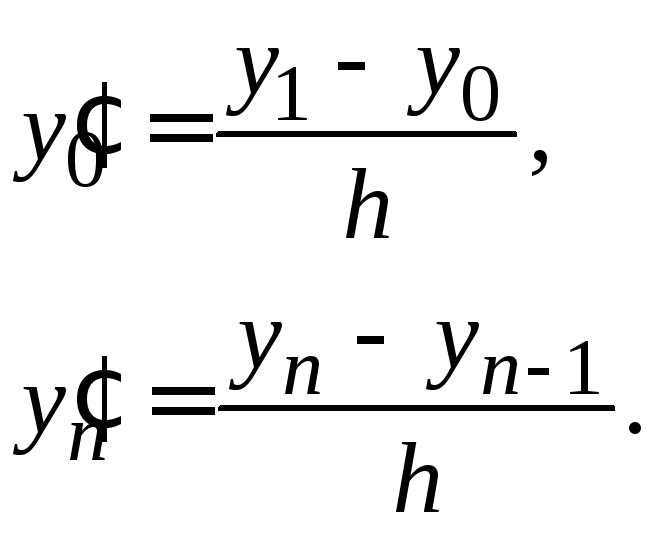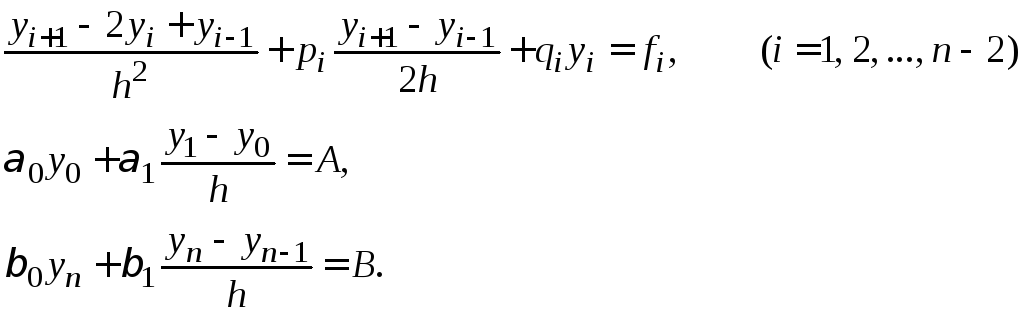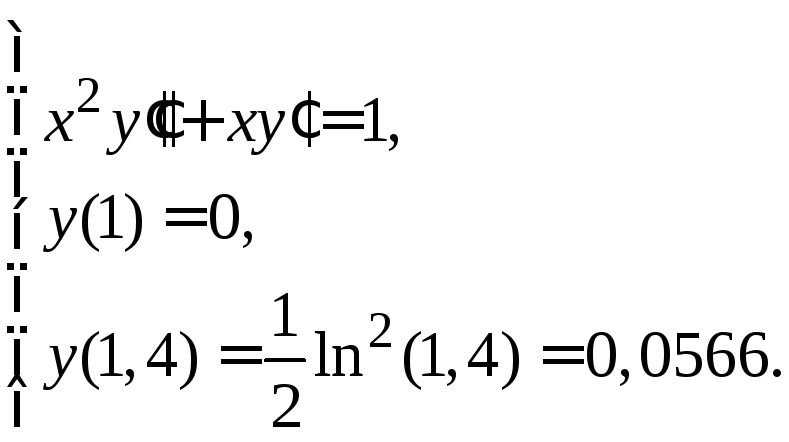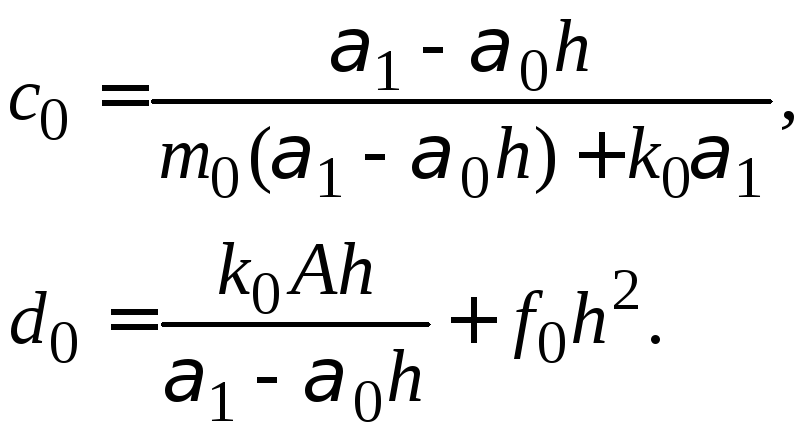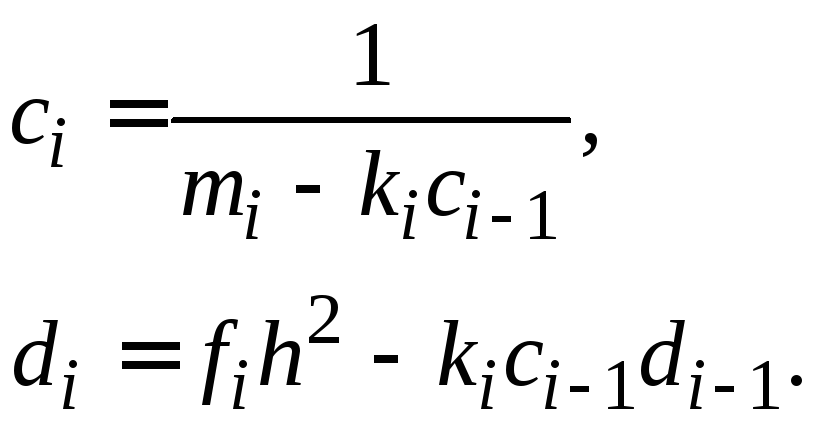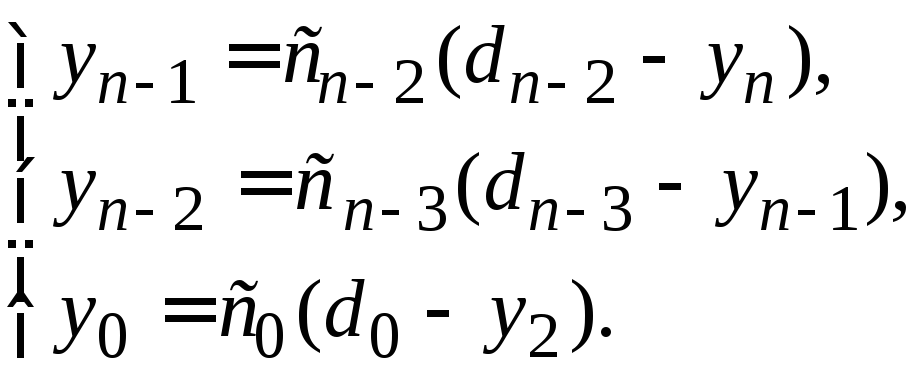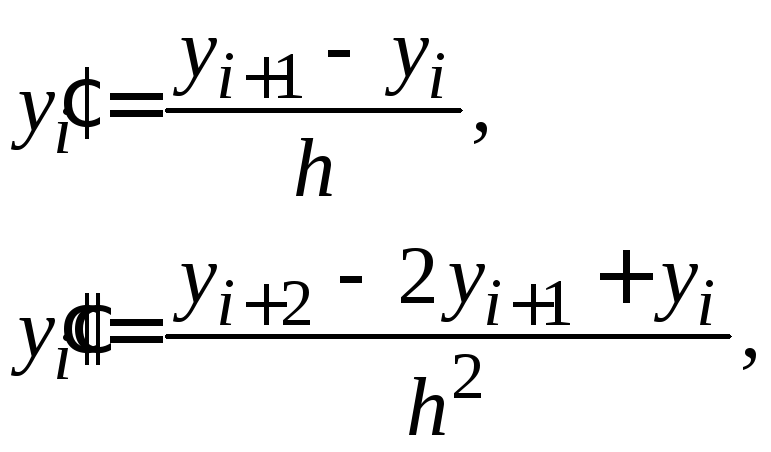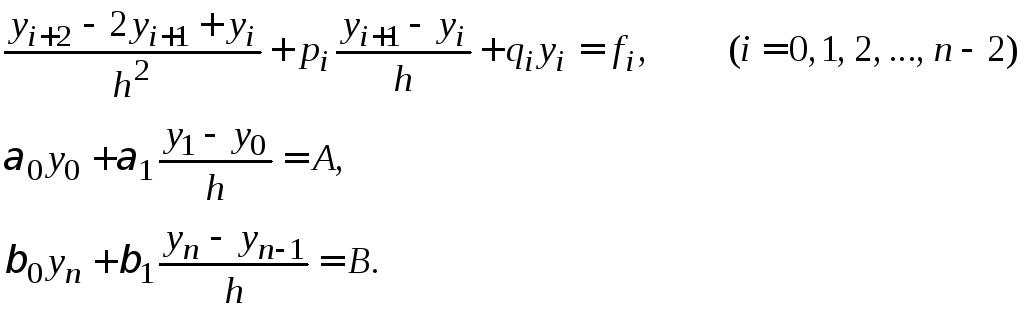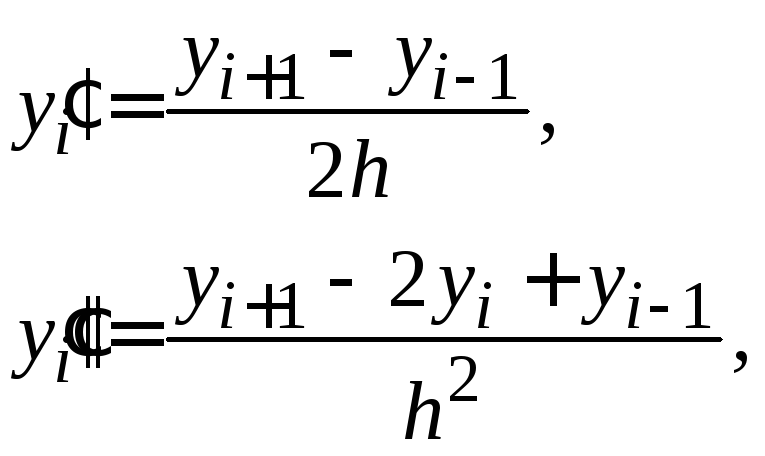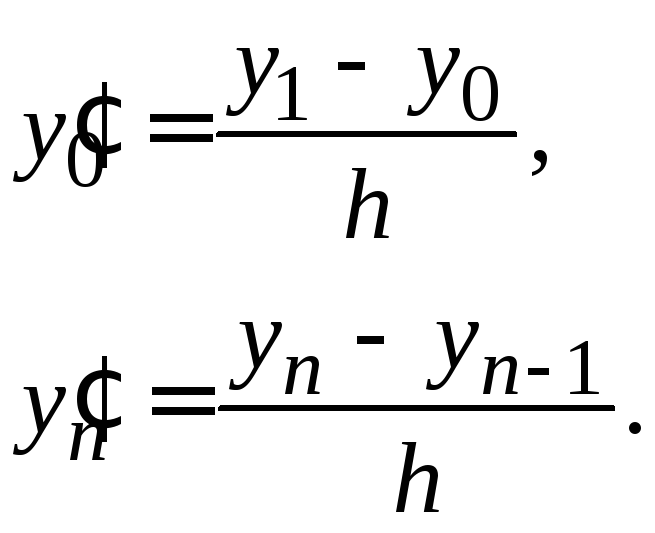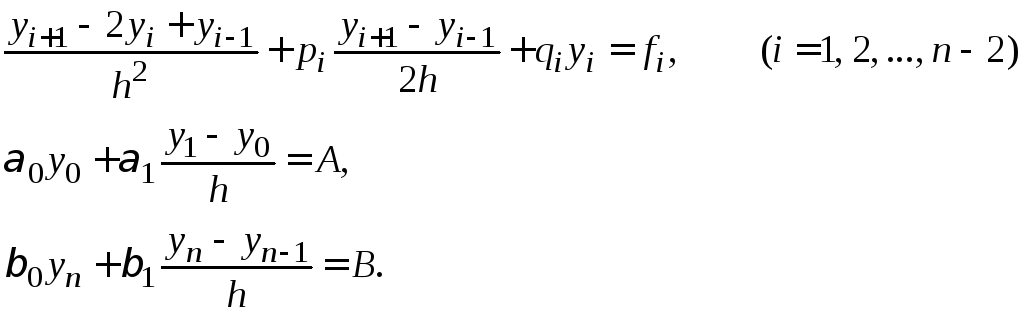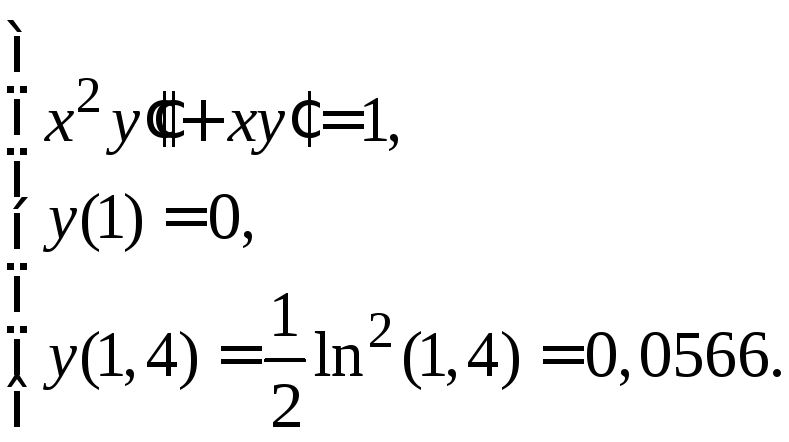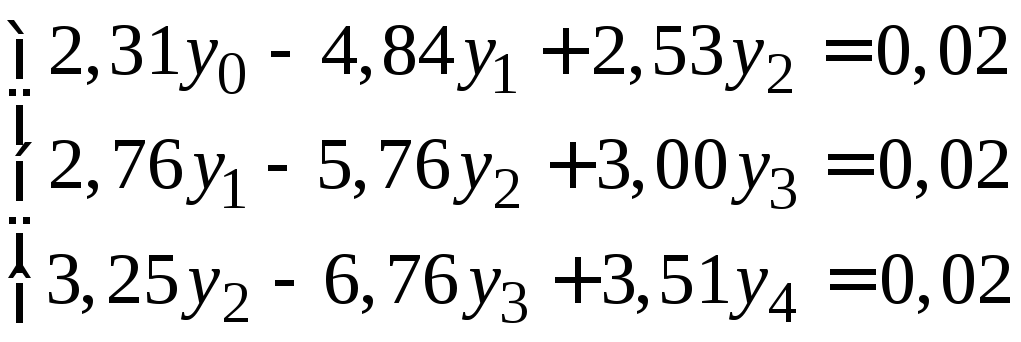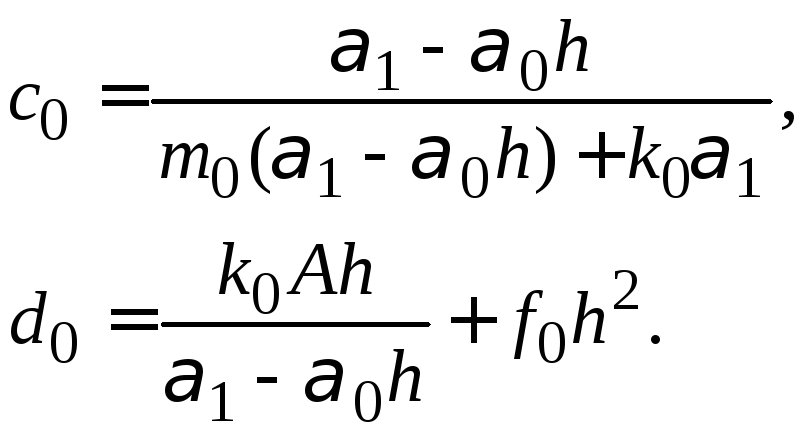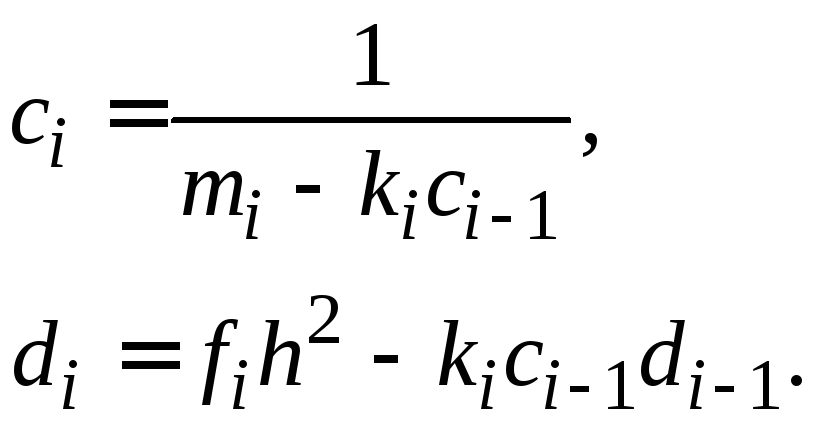1. Математическое моделирование и вычислительный эксперимент. Схема вычислительного эксперимента. Требования к вычислительным методам. Виды погрешностей. Основные задачи теории погрешностей, способы их решения. Применение дифференци­ального исчисления при оценке погрешности. Обратная задача теории погрешностей. Оценка погрешностей вычислений, возникающих в ЭВМ.

Математическое моделирование и вычислительный эксперимент. Схема вычислительного эксперимента.

1. Построение мат.мод. 2. Постр.алгоритма реш. 3. Реализация алгоритма на ЭВМ 4. Анализ рез-в.

Виды погрешностей.

При практических вычислениях обычно используют приближенные значения величин – приближенные числа.

Погрешность приближенного числа a, т.е. разностьмежду ним и точным значением, как правило, неизвестна.

Под оценкой погрешности приближенного числа aпонимают установление неравенства вида

(1.1)

Число называетсяабсолютной погрешностью(иногда употребляется термин «предельная абсолютная погрешность»). Это число определяется неоднозначно: его можно увеличить. Обычно указывают возможно меньшее число, удовлетворяющее неравенству (1.1).

Абсолютные погрешности записывают не более чем с двумя-тремя значащими цифрами (при подсчете числа значащих цифр не учитывают нулей, стоящих слева, например, в числе 0,010030 имеется 5 значащих цифр). В приближенном числе aне следует сохранять те разряды, которые подвергаются округлению в его абсолютной погрешности.

Относительной погрешностьюприближенного числаaназывается отношение его абсолютной погрешностик абсолютной величине числаa, т.е..

Относительная погрешность обычно выражается в процентах, и ее принято записывать не более чем с двумя-тремя значащими цифрами.

Во многих технических приложениях принято характеризовать точность приближенных чисел их относительной погрешностью.

Формулы точного подсчета погрешностей результатов действий над приближенными числами

;

;

, где – абсолютная погрешность приближенного числа,– относительная погрешность приближенного числа,– рациональное число.

Формулы погрешности вычисления значений функции от одной переменной

–абсолютная погрешность дифференцируемой функции , вычисленная в точке,.

–относительная  погрешность дифференцируемой функции , вычисленная в точке.

Рассмотрим правила вычисления без строгого учета погрешностей

Правило 1. Если число слагаемых невелико, то в алгебраической сумме приближенных значений чисел, в записи которых все цифры верны, следует оставлять столько десятичных знаков, сколько их имеет слагаемое с наименьшим числом десятичных знаков. Слагаемые с большим числом десятичных знаков следует предварительно округлить на один десятичный знак больше, чем у выделенного слагаемого.

Правило 2. Если число исходных знаков невелико, то в произведении (частном) приближенных значений чисел следует оставлять столько значащих цифр, сколько их имеет число с наименьшим количеством значащих цифр. Исходные данные с большим числом значащих цифр следует предварительно округлить, оставив на одну значащую цифру больше, чем у выделенного исходного данного.

Правило 3. При возведении приближенного значения числа в квадрат или куб, а также при извлечении квадратного корня или кубического корня в результате следует оставлять столько значащих цифр, сколько их имеет соответственно основание степени или подкоренное выражение.

Правило 4. При выполнении последовательно ряда действий над приближенными значениями чисел следует в промежуточных результатах сохранять на одну цифру больше, чем рекомендуют предыдущие правила. При округлении окончательного результата запасная цифра отбрасывается.

2. Приближенное решение нелинейных уравнений: постановка задачи, отделение корней, уточнение корней (методы половинного деления, Ньютона, хорд, простых итераций). Алгоритм и расчетные формулы, геометрическая интерпретация, сходимость методов, сопоставление методов.

Общие сведения о методах решения нелинейных уравнений

Нелинейные уравнения делятся на два класса – алгебраические и трансцендентные. Алгебраическими называются уравнения, содержащие только алгебраические функции (целые, рациональные, иррациональные). В частности, многочлен является целой алгебраической функцией. Уравнения, содержащие другие функции (тригонометрические, показательные, логарифмические и др.), называются трансцендентными.

Методы решения нелинейных уравнений делятся прямые и итерационные. Прямые методы позволяют записать корни в виде некоторого конечного соотношения (формулы). На практике, как правило, уравнений не решаются такими простыми методами. Для их решения обычно используются итерационные методы, т.е. методы последовательных приближений. Алгоритм нахождения корня уравнения с помощью итерационного метода состоит из двух этапов: а) отыскание приближенного значения корня или содержащего его отрезка; б) уточнения приближенного значения до некоторой заданной степени точности.

Пусть задано уравнение на множестве действительных чисел.

. (2.1.)

Приближенное значение корня (начальное приближение) уравнения (2.1) может быть найдено различными способами: из физических соображений, из решения аналогичной задачи при других исходных данных, с помощью графических методов. Если такие априорные оценки исходного приближения провести не удается, то находят две близко расположенные точки aиb, в которых непрерывная функцияf(x) принимает значения разных знаков, т.е.f(a)f(b)<0. В этом случае между точкамиaи bнаходится, по крайней мере, одна точка, в которойf(x)=0. В дальнейшем будем предполагать, чтоисохраняют знак на отрезке [a; b].

Метод половинного деления

Метод половинного деления состоит в разделении отрезка [a; b] пополам точкой. Если (что практически наиболее вероятно), то возможны два случая: либоf(x) меняет знак на отрезке [a; c]; либо на отрезке [c; b].

Выбирая в каждом случае тот из отрезков, на котором функция меняет знак, и, продолжая процесс половинного деления дальше, можно дойти до сколь угодно малого отрезка, содержащего корень уравнения.

Рассмотренный метод можно использовать как метод решения уравнения с заданной точностью. Действительно, если на каком-то этапе процесса получим отрезок [c; c'], содержащий корень, то, приняв приближённо, получим ошибку, не превышающую, значения.

Метод хорд

Предположим, что на отрезке [a; b] функцияf(x)удовлетворяет следующим условиям:

. (2.2)

Последовательные приближения точного корня вычисляются по формулам:

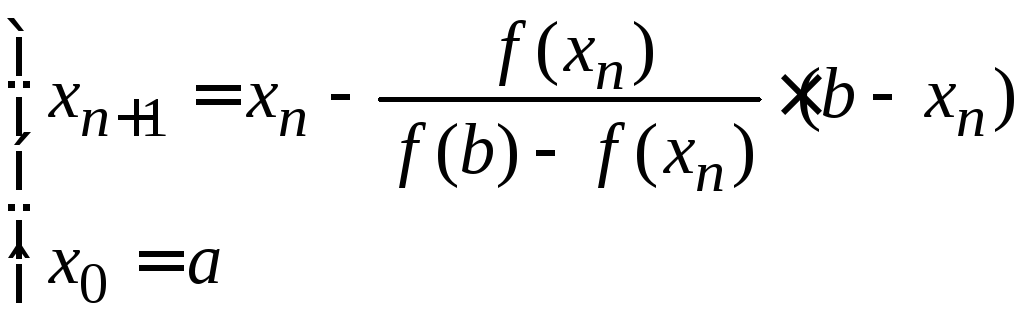. (2.3)

Если условие (2.2) не выполняется, а имеет место неравенство

, (2.4)

то последовательные приближения вычисляются по формулам:

. (2.5)

Метод касательных (Ньютона)

По методу касательных вычисления проводятся по формулам:

(2.6)

при выполнении условия (2.4).

При выполнении условия (2.2) используются расчетные формулы:

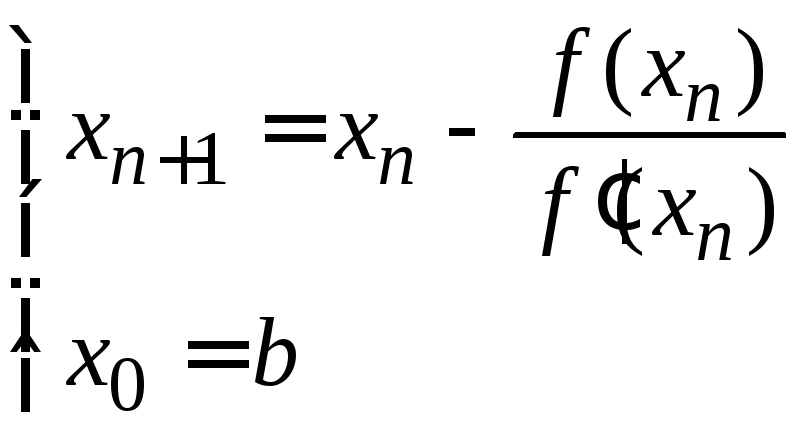. (2.7)

Оценка погрешности метода хорд и метода касательных может быть вычислена по формуле:

, где ,x^*– точный корень, а– приближенный корень уравнения (2.1).

Комбинированный метод хорд и касательных

Комбинированный метод основан на одновременном использовании методов хорд и касательных.

В результате получим две монотонные последовательности {x_п},{x'_п}- приближенные значения корня по недостатку и по избытку соответственно.. Для нахождения корняξс заданной степенью точности достаточно ограничится теми значениями, для которых. Так как, то в качестве значения корня следует взять среднее арифметическое чисел, т. е. число. Легко видеть, что.

Расчётные формулы:

а) если на [a; b], то:

.

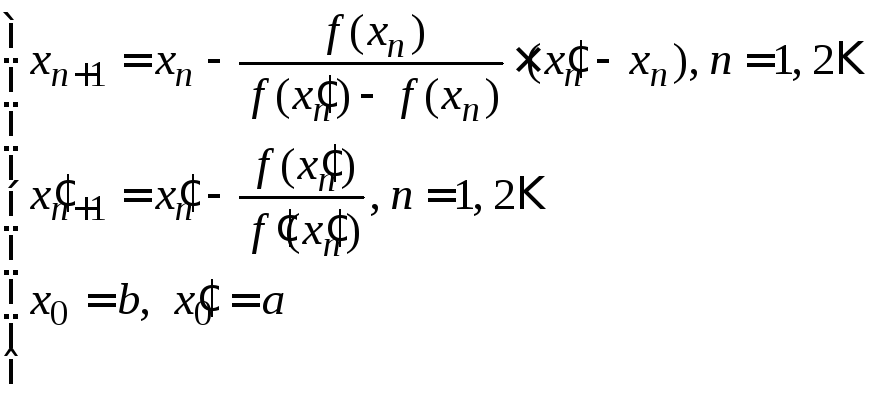б) если на [a; b], то:

.

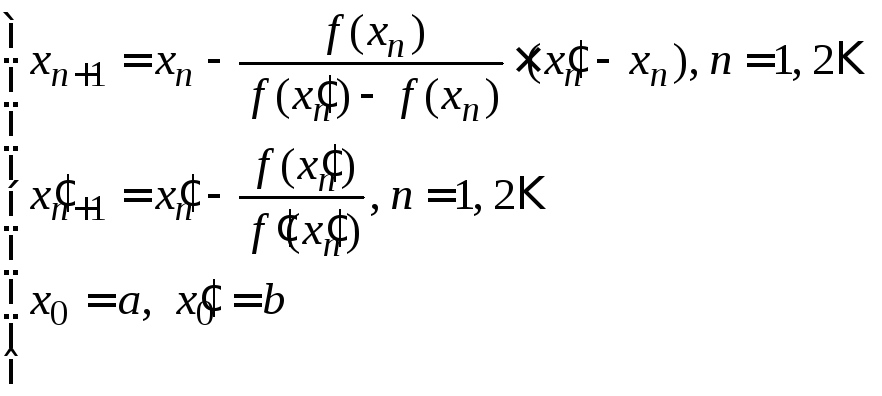Пример 2.1. Дано уравнение . Исследовать вопрос о существовании и единственности корняξ на отрезке [0,5; 1,5]. Вычислить три приближения корня уравнения по методу хорд и по методу касательных.

Вычисляем знак выражения , где . Т. к.инепрерывная функция на отрезке [0,5; 1,5], то уравнение имеет хотя бы один корень на заданном отрезке.

1. Для доказательства единственности корня вычисляем f '(x), f ''(x)и определим их знак на отрезке [0,5; 1,5].

, ,f''(x)>0 на отрезке [0; 1], следовательно,f(x) монотонно возрастает, и корень уравнения на отрезке [0; 1] единственный;, следовательно, функция сохраняет на отрезке выпуклость. Т.к., то для вычисления приближенных значений корня по методу хорд используются формулы (2.3), а по методу касательных (2.7).

Используя данные формулы, получаем ответ:

–приближенные значения корня по методу хорд; – приближенные значения корня по методу касательных.

Метод простой итерации

Для использования этого метода исходное нелинейное уравнение записывается в виде

. (2.8)

Пусть известно начальное приближение корня x=x₀

Подставляя это значение в правую часть уравнения (2.8), получаем новое приближение: c₁=f(c₀). Подставляя каждый раз новое значение корня в правую часть уравнения (2.8), получаем последовательность значений:

, (2.9)

Итерационный процесс прекращается, если результаты двух последовательных итераций близки .

Достаточным условием сходимости метода простой итерации является условие на множестве действительных чисел.

Достаточным условием сходимости метода простой итерации на отрезке [a;b] является условие,[a;b].

Для более точной оценки погрешности используются формулы:

,

где , на множестве [a;b].

Пример 2.2. Вычислить четыре приближения методом простой итерации для уравнения .

Для исследования выберем отрезок [0; 3].

1) Функция определена и имеет в каждой точкеx из отрезка [0; 3] производную:.

2) Значения функции удовлетворяют неравенству:

, т. е. все значения функции содержатся в отрезке [0; 3].

3) Производная функции удовлетворяет неравенству:

, т. е. существует такое, что для всехxиз отрезка [0; 3] имеет место неравенство:. Следовательно, выполнено достаточное условие применимости метода простой итерации на отрезке.

Выберем произвольно из отрезка [0; 3], например. Используя формулу (2.9), получаем четыре приближенных значения корня:

Оценим погрешность четвертого приближения:

.

3. Численное решение систем нелинейных уравнений. Методы простой итерации, Ньютона и их модификации. Оценка погрешности методов.

Метод Ньютона для систем нелинейных уравнений.

Пусть дана система:

Согласно методу Ньютона последовательные приближения вычисляются по формулам:

,

где

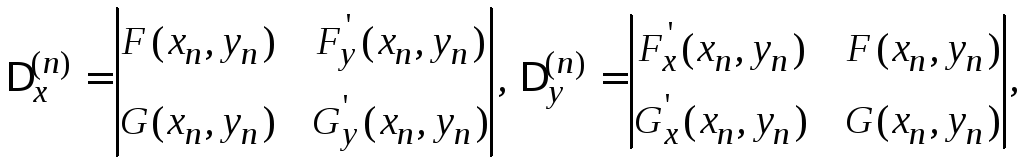
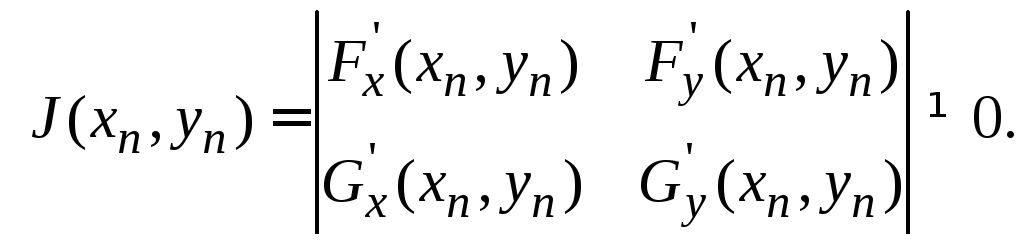
Начальные приближения определяются приближенно (например, графически).

Метод Ньютона эффективен только при достаточной близости начального приближения к решению системы.

Пример 3.3. Найти одно приближение для решения системы. За начальное приближение системы принять .

.

Вычисляем в начальной точке :

.

Получаем первые приближения:

.

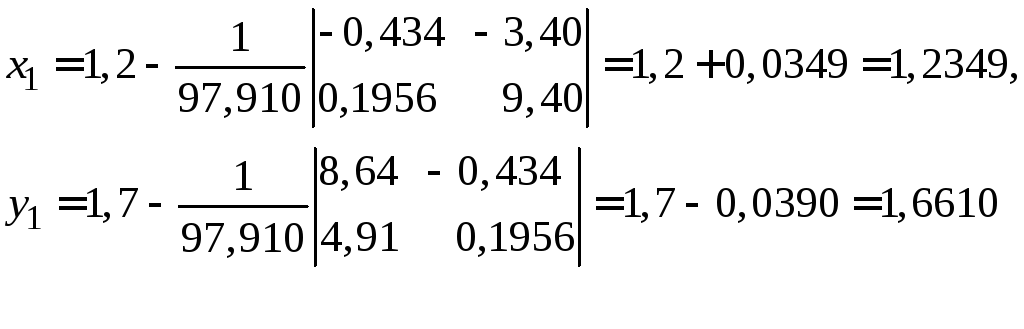4. Численные методы решения систем линейных алгебраических уравнений (СЛАУ). Прямые методы решения СЛАУ: основные идеи методов, условия применимости, вычислительные затраты. Итерационные методы решения СЛАУ: примеры методов, условия сходимости, оценка погрешности методов.

Метод Гаусса с выбором главного элемента для системы линейных уравнений

Система из плинейных уравнений спнеизвестными вида:

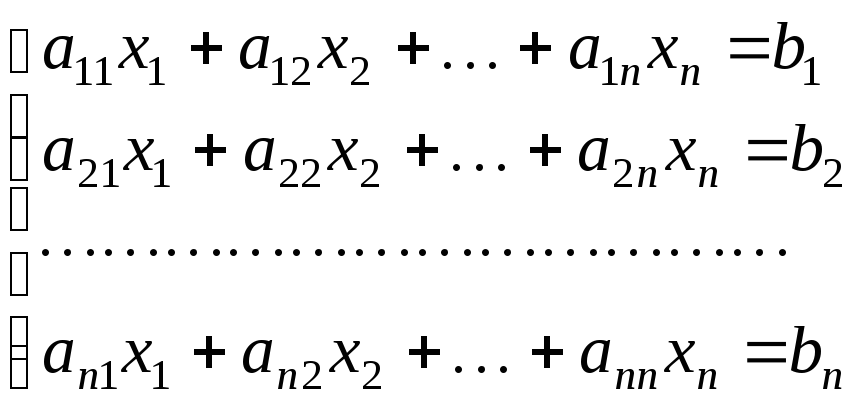(3.1)

имеет единственное решение при условии: , где

­ матрица коэффициентов системы (3.1)

К точным методам относится метод Гаусса с выбором главного элемента. Среди элементов матрицыАвыберем наибольший по модулю, называемый главным элементом. Пусть им будет элемент. Строка с номеромр, содержащая главный элемент, называется главной строкой. Далее вычисляем множители:для всех. Затем преобразуем матрицу следующим образом: из каждой неглавной строки вычитаем почленно главную строку, умноженную наm_i. В результате получим матрицу, у которой все элементыq-го столбца, за исключением, равны нулю. Отбрасываем этот столбец и главную строку и получаем новую матрицус меньшим на единицу числом строк и столбцов. Над матрицейповторяем аналогичные операции, после чего получаем матрицуА₂и т. д.

Такие преобразования продолжаем до тех пор, пока не получим матрицу, содержащую одну строку, которую считаем тоже главной. Затем объединяем все главные строки, начиная с последней. После некоторой перестановки они образуют треугольную матрицу, эквивалентную исходной. На этом заканчивается этап вычислений, называемый прямым ходом. Решив систему с полученной треугольной матрицей коэффициентов, найдём последовательно значения неизвестных . Этот этап вычислений называется обратным ходом.

Смысл выбора главного элемента состоит в том, чтобы сделать достаточно малым число m_iи тем самым уменьшить погрешность вычислений.

Вычисление обратной матрицы для системы линейных уравнений

Пусть дана невырожденная матрица , где (i, j = 1, 2,…,n). Для нахождения элементов обратной матрицы , где (i, j = 1, 2,…n) воспользуемся основным соотношением:

АА^-1 =Е, гдеЕ – единичная матрица.

Перемножая матрицы АиА^-1 и используя равенство их матрицеЕ, получимпсистем линейных уравнений вида:

(i = 1, 2, …, n; j – фиксировано), где.

Полученные псистем линейных уравнений имеют одну и ту же матрицуАи различные столбцы свободных членов. Эти системы можно решать методом Гаусса (см. п. 3.1.1). В результате решения систем получаем единичную матрицуA.

Метод простой итерации для систем линейных уравнений

Метод простой итерации даёт возможность получить последовательность приближённых значений, сходящуюся к точному решению системы.

Преобразуем систему (3.1) к нормальному виду:

.                                                 (3.2)

Правая часть системы (3.2) определяет отображение:

, преобразующее точку -мерного метрического пространства в точкутого же пространства.

Выбрав начальную точку , можно построить итерационную последовательность точекп- мерного пространства:

При определённых условиях данная последовательность сходится.

Так, для исследования сходимости таких последовательностей используется принцип сжимающих отображений, который состоит в следующем.

Если F – сжимающее отображение, определённое в полном метрическом пространстве с метрикой, то существует единственная неподвижная точка, такая, что. При этом итерационная последовательность,, полученная с помощью отображенияFс любым начальным членомх⁽⁰⁾, сходится к.

Оценка расстояния между неподвижной точкой отображенияF и приближениемх^(к)даётся формулами:

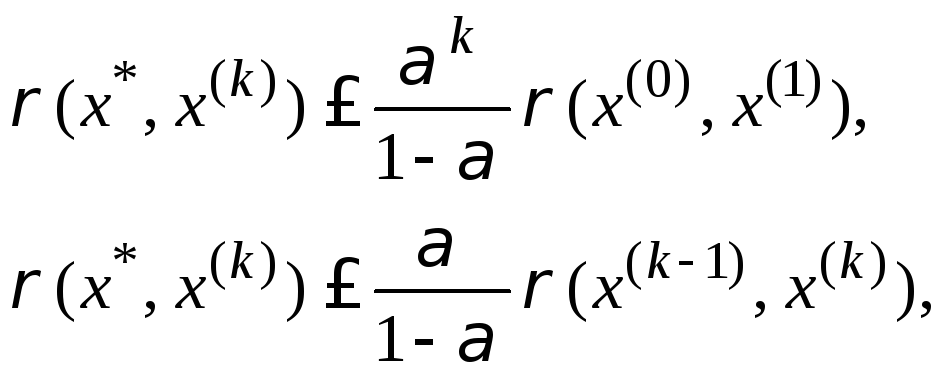(3.3)

где α– множитель, определяемый достаточными условиями сжимаемости отображенияF.

Значение множителя α, определяется выбором метрики, в которой проверяется сходимость последовательности значений.

Рассмотрим Достаточные условия сходимости итерационной последовательности .

Практически, для применения метода итерации систему линейных уравнений удобно "погрузить" в одну из трёх следующих метрик:

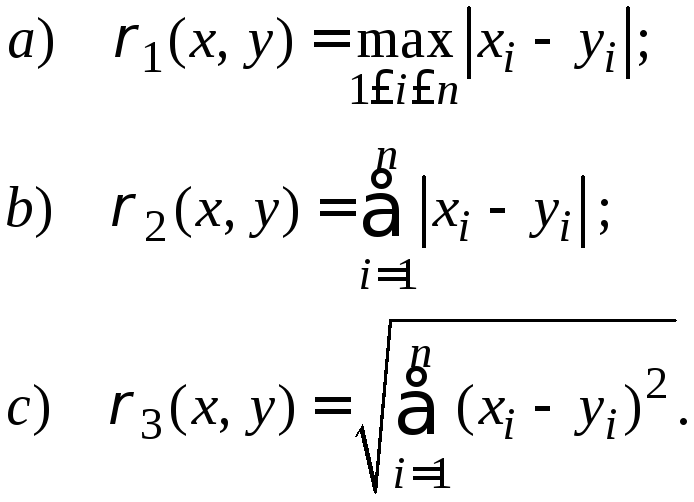(3.4)

Для того, чтобы отображение F, заданное в метрическом пространстве соотношениями (3.2), было сжимающим, достаточно выполнение одного из следующих условий:

а) в пространстве с метрикой :, т. е. максимальная из сумм модулей коэффициентов в правой части системы (3.2), взятых по строкам, должна быть меньше единицы.

б) в пространстве с метрикой :, т. е. максимальная из сумм модулей коэффициентов в правой части системы (3.2), взятых по столбцам, должна быть меньше единицы.

в) в пространстве с метрикой : , т. е. сумма квадратов при неизвестных в правой части системы (3.2) должна быть меньше единицы

Пример 3.1. Вычислить два приближения методом простой итерации. Оценить погрешность второго приближения. В качестве начального приближения выбрать .

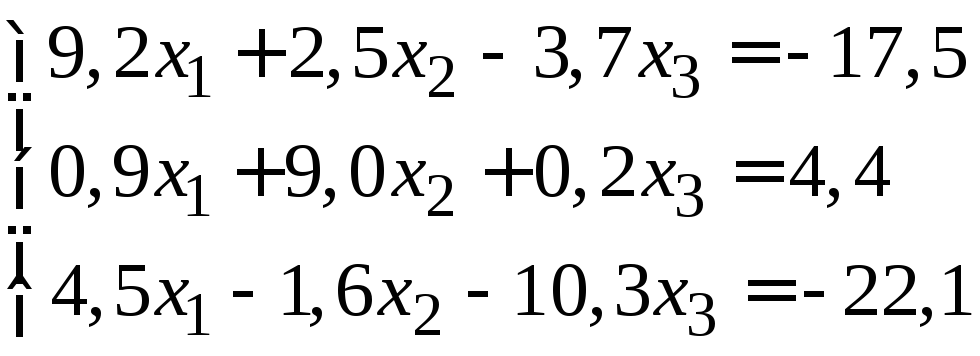
Так как диагональные элементы системы являются преобладающими, то приведем систему к нормальному виду:

Последовательные приближения будем искать по формулам:

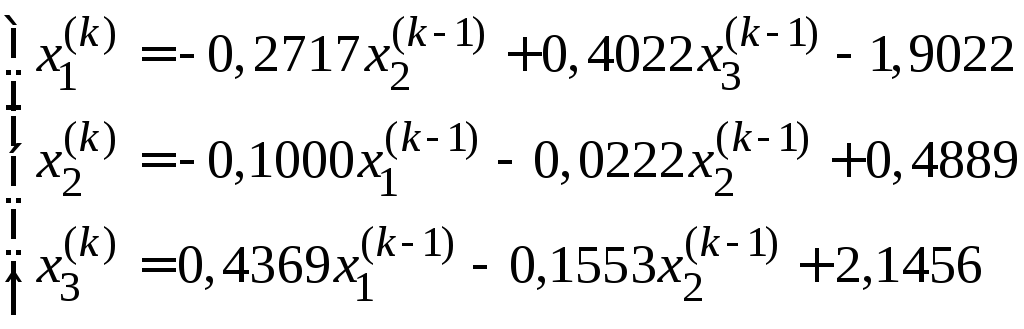
Получаем: ,.

Для оценки погрешности в метрике вычисляем коэффициент.

Вычисляем погрешность:

Метод Зейделя для систем линейных уравнений

Метод Зейделя является модификацией метода простой итерации. Вычисление проводится по следующим формулам:

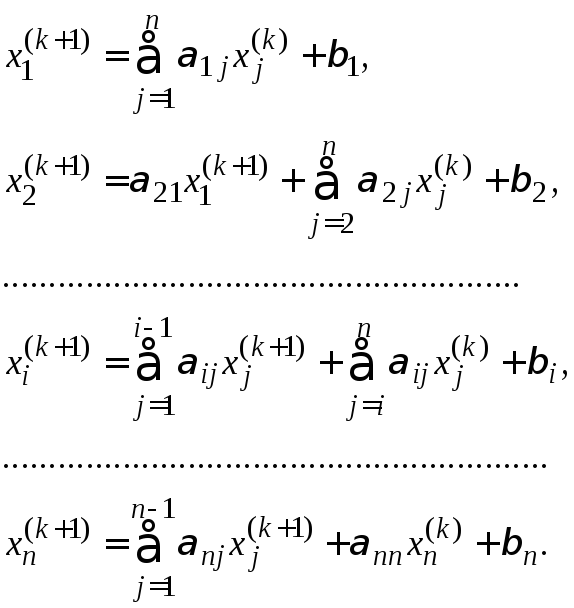
Достаточные условия сходимости итерационной последовательности приближенных решений системы и оценка погрешности проводятся по тем же формулам, что и в методе простой итерации.

Пример 3.2. Рассмотрим вычисление двух приближений по методу Зейделя для примера, решенного выше для метода простой итерации и оценим погрешность.

Вычисления будем проводить по формулам:

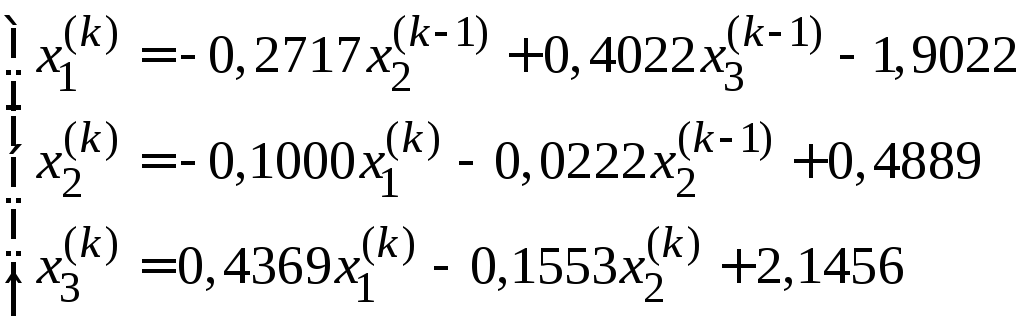
Выбираем начальное приближение: и получаем:

, .

.

5. Численное интегрирование. Квадратурные формулы Ньютона–Котеса. Формула трапеций, формула Симпсона. Погрешность квадратурных формул. Интегрирование с помощью степенных рядов. Метод Монте-Карло.

Квадратурные формулы Ньютона - Котеса

В тех случаях, когда для вычисления определённого интеграла по каким-либо причинам не представляется возможным использовать формулу Ньютона - Лейбница, применяют численные методы вычисления интеграла. Многие из них основаны на том, что на отрезке [a, b] функциюf(x)заменяют интерполирующей функцией.

Разобьём отрезок интерполирования [a, b] напчастей. Получимточку, где . Заменим функциюf(x)на отрезке [a;b] интерполяционным многочленом Лагранжа для равноотстоящих узлов. Обозначим значения функции в узлах интерполяции:.

,

где .

Положим:

Сделаем замену: ,.

При имеемt = 0, а приимеем t = n. Получаем:

(6.1)

где (6.2)

Формула (6.1) называется квадратурной формулой Ньютона - Котеса, а (6.2) называются коэффициентами Котеса.

Формула трапеций

При из формулы (6.1), (6.2) получаем:

(6.3)

Формула (6.3) даёт один из простейших способов вычисления определённого интеграла и называется формулой трапеций. Распространяя формулу (6.3) на все отрезки разбиения, получим общую формулу трапеций на отрезке [a;b]:

(6.4)

Оценка погрешности метода трапеции:

, где (6.5)

Формула Симпсона

При из формул (6.1), (6.2) имеем:.

Получаем на отрезке :

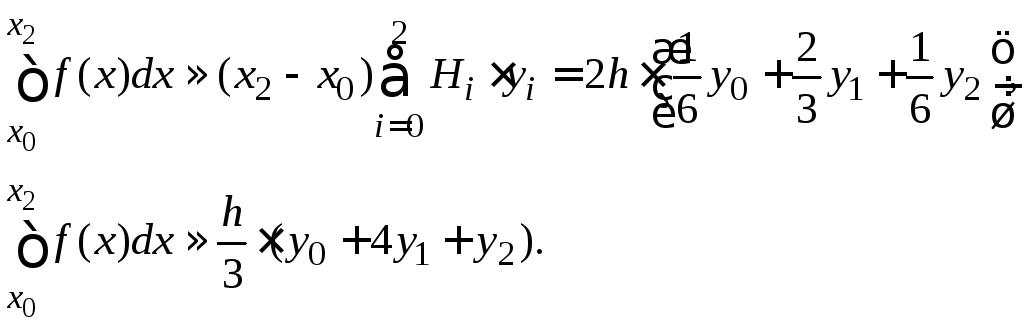(6.6)

Если , то применяя формулу (6.6) к каждой паре частичных отрезков(i = 1, 2, …m) получим:

Формула (6.7) называется формулой Симпсона.

Оценка погрешности формулы Симпсона:

, где .

Иногда удобно использовать следующую оценку: , где – значения интеграла, вычисленные по формуле Симпсона соответственно припи2потрезках разбиения.

Пример 6.1. Вычислить интеграл: по формуле трапеций, разделив отрезок [0; 1] на 5 равных частей и оценить погрешность вычислений. Значения подынтегральной функции приведены в таблице:

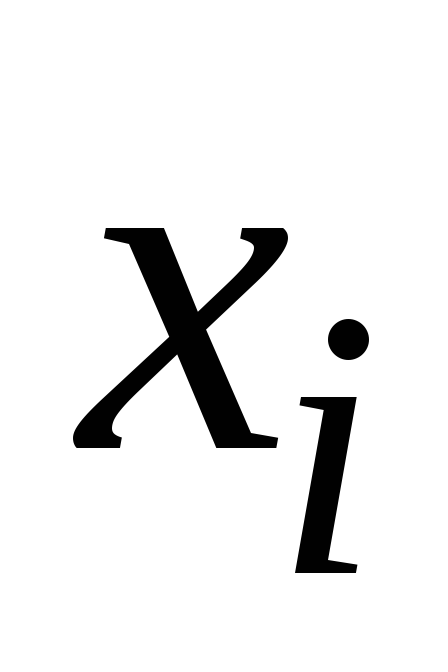
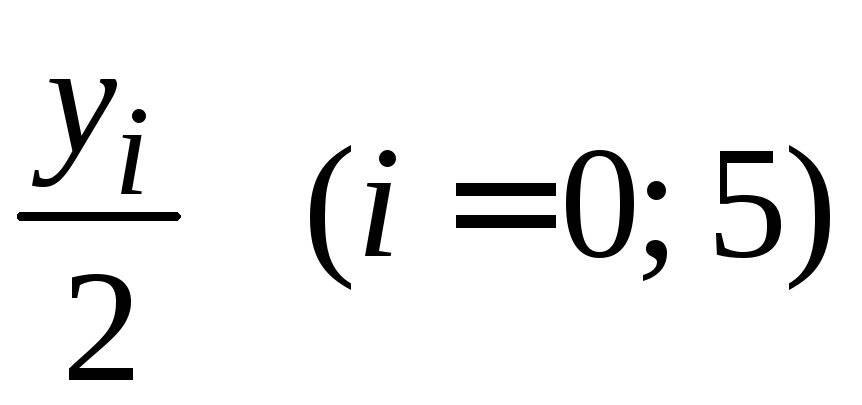
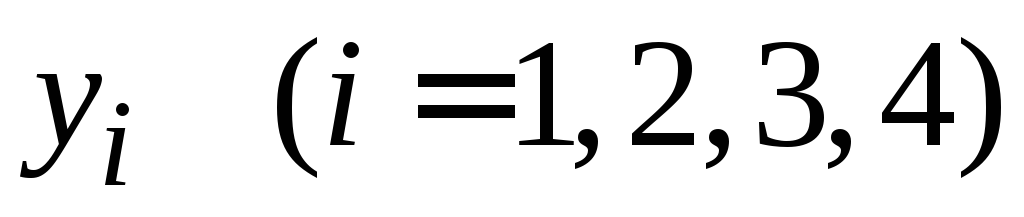
0,0 0,2 0,4 0,6 0,8 1,0	0 0,4207355	0,0079467 0,0623068 0,2032711 0,4591078
Σ	0,4207355	0,7326324

I=0,2ּ(0,4207355+0,7326324)=0,2306736.

Оценка ошибки метода: На отрезке [0; 1] . Получаем.

Пример 6.2. Вычислить интеграл: по формуле Симпсона, разделив отрезок [0; 1] на 10 равных частей и оценить погрешность вычислений. Значения подынтегральной функции приведены в таблице 6.1.

.

Для оценки остаточного члена найдём производную четвёртого порядка от подынтегральной функции.

Таблица 6.1

Значения функции для примера 6.1.

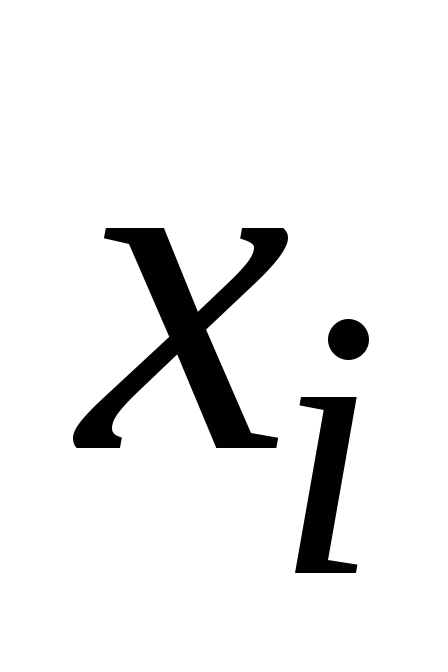
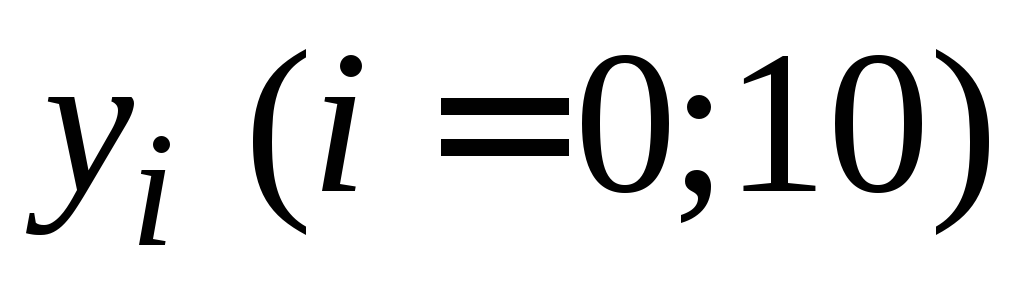
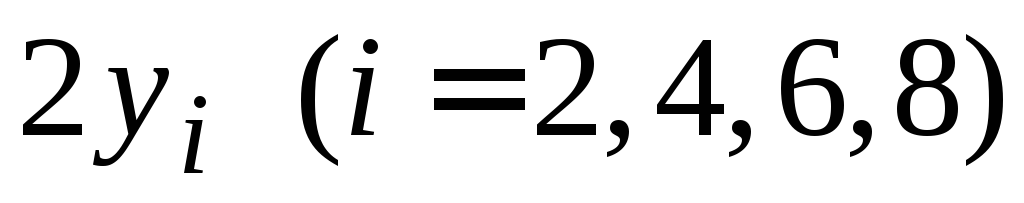
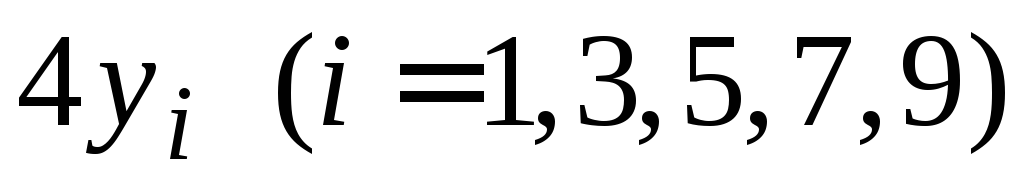
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0	0,841471	0,0158944 0,1246436 0,4065422 0.9182156	0,0039932 0,1063872 0,4794248 1,2626666 2, 537972
Σ	0,841471	1,4652648	4,390471

Вычисление интегралов методом Монте - Карло

В практических приложениях часто приходится вычислять значения кратных интегралов. Кратный интегралвычисляется для функции многих переменных по замкнутой ограниченной многомерной области. Вычислительная схема имеет вид: интервал, соответствующий изменению каждой переменной внутри области интегрирования, разбивается на фиксированное число отрезков. Таким образом, задается разбиение области интегрирования на определенное число элементарных многомерных объемов. Вычисляются значения подынтегральной функции для точек, взятых по одной внутри каждого элементарного объема, и полученные значения суммируются. При увеличении кратности интеграла число слагаемых очень быстро возрастает. Пусть, например, мы разбиваем интервализменения каждой переменной на десять частей. Для вычисления 10-кратного интеграла потребуется сумма, количество слагаемых в которой определяетсячислом 10¹⁰. Вычисление такой суммы затруднительно даже на самых быстродействующих современных ЭВМ. В таких ситуациях предпочтительнее использовать для получения значения интеграламетод Монте - Карло. В основе оценки искомого значения интеграла I лежит известное соотношение: где – значение подынтегральной функции в некоторой «средней» точке области интегрирования, а – (многомерный) объем области интегрирования. При этом предполагается, что подынтегральная функция (обозначим ее ) непрерывна в области интегрирования. Выберем в этой области n случайных точек M_i. При достаточно большом n приближенно можно считать:

(6.8)

Точность оценки значения интеграла методом Монте-Карло пропорциональна корню квадратному из числа случайных испытаний и не зависит от кратности интеграла. Именно поэтому применение метода целесообразно для вычисления интегралов высокой кратности. Рассмотрим применение метода для простейшего случая интеграла: .

В этой ситуации и равенство (6.8) принимает вид:, где– случайные точки, лежащие в интервале [a;b]. Для получения таких точек на основе последовательности случайных точек, равномерно распределенных в интервале [0; 1], достаточно выполнить преобразование: .

Рассмотрим пример вычисления интеграла вида , где- замкнутая область на плоскости.

Пример 6.1. Методом Монте-Карло вычислить: .

Область интегрирования определяется следующими неравенствами:

.

Область интегрирования расположена внутри единичного квадрата

Для решения задачи воспользуемся таблицей случайных чисел, представленных в [2]. При проведении расчетов для случая n=20 (при использовании компьютера обычно используются большие значенияn) получаем: из 20 пар случайных чисел из единичного квадрата только четыре точки попали в область.

Подсчитав сумму значений для точек, которые попали в область, получаем:

6. Численное дифференцирование. Особенность задачи численного дифференцирования. Дифференцирование на основе интерполяционных многочленов. Оценка погрешности.

Численное дифференцирование на основе интерполяционной формулы Лагранжа

Пусть f(x)– функция, для которой нужно найти производную в заданной точке отрезка [a, b],F_n(x)– интерполяционный многочлен дляf(x), построенный на [a, b].

, где R_n(x)– погрешность интерполяции.

–погрешность производной.

, где

.

Пользуясь выражением для остаточного члена интерполяционной формулы, можно получить:

. (5.1)

В узлах интерполяции формула (5.1) примет вид:

.

Численное дифференцирование на основе интерполяционной формулы Ньютона

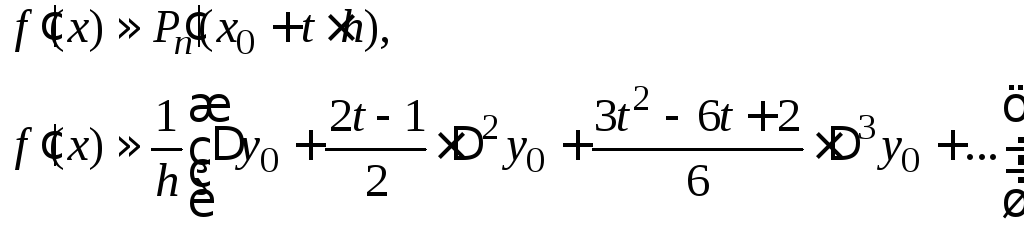(5.2)

Таким же образом можно вычислить и производные любого порядка. Формула (5.2) существенно упрощается, если хсовпадает с узлом интерполирования. В этом случае каждый узел можно считать начальным:х = х₀, t = 0.

.

Оценка погрешности:

.

В случае оценки погрешности в узле таблицы (х=х₀, t=0) будем иметь:

.

Для оценки при малыхhиспользуют формулу:.

7. Интерполирование функций. Интерполяция алгебраическими многочленами (многочлены Лагранжа и Ньютона). Погрешность интерполяционных формул. Интерполирование сплайнами.

Постановка задачи численного интерполирования

Пусть на отрезке [а; b] заданы точки, которые называются узлами интерполяции.Будем предполагать, что все точкиразличны и расположены в порядке возрастания.

Пусть известны значения некоторой функции в этих точках:

.(4.1)

Требуется в определенном классе функций построить такую функцию , значения которой в узлах интерполяции совпадают со значениями. Функциюбудем называть интерполирующей функцией.

Будем искать интерполирующую функцию в виде интерполяционного многочленаn-й степени:

. (4.2)

Условия (4.1) в данном случае перепишутся:

(4.3)

Коэффициенты многочлена (4.2) находятся единственным образом из условий (4.3). Рассмотрим различные способы записи интерполяционного многочлена.

Интерполяционный многочлен Лагранжа. Схема Эйткена

Пусть функция задана условиями (4.1). Интерполяционным многочленом Лагранжа называется многочлен, представленный в виде:

. (4.4)

Оценка погрешности формулы Лагранжа: ,

где (4.5)

Пример 4.1. Для функции, имеющей аналитическое выражение , задана интерполяционная таблица:

	100	121	144
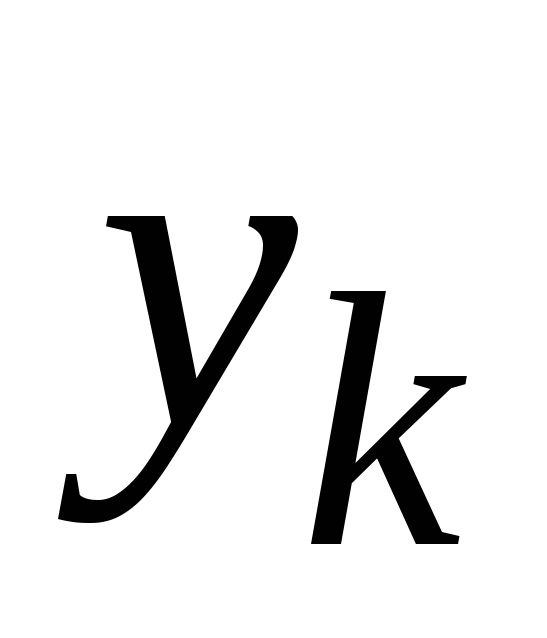
	10	11	12

а) Составить интерполяционный многочлен второго порядка.

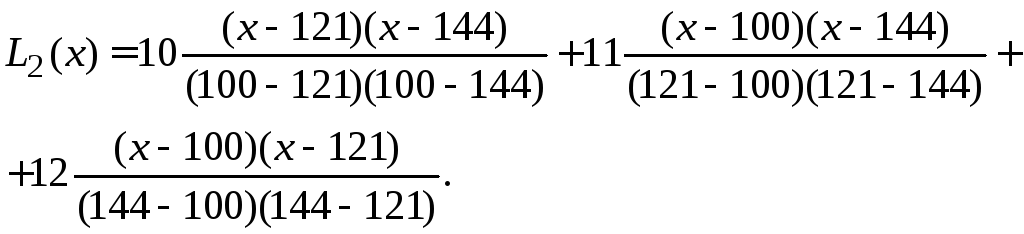
б) Вычислить значение L₂(115).

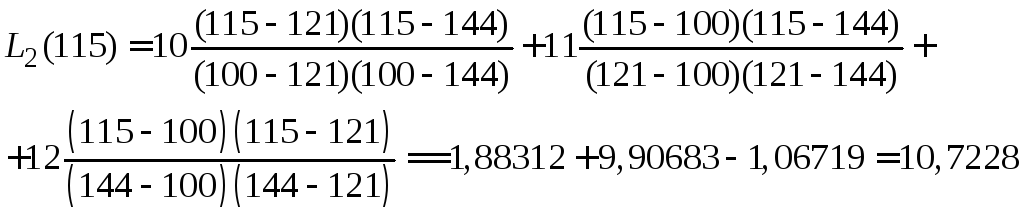
в) Оценить погрешность полученного результата

,

Если надо вычислить не общее выражение , а лишь его значение на конкретноми при этом значения функции даны в достаточно большом количестве узлов, то можно использовать интерполяционную схему Эйткена.

Согласно данной схеме последовательно вычисляются многочлены:

,

,

и т.д.

Интерполяционный многочлен n-й степени, принимающий в точках значения(), запишется следующим образом:

.

Вычисления   по схеме Эйткена удобно расположить в таблице 4.1.

Таблица 4.1

Интерполяционная схема Эйткена

						…
						…
						…

Вычисления по схеме Эйткена обычно ведутся до тех пор, пока последовательные значения ине совпадут в пределах заданной точности. Схема Эйткена легко реализуется на ЭВМ и обеспечивает возможность автоматического контроля точности вычислений.

Пример 4.2. Функция задана таблицей.

	1.0	1.1	1.3	1.5	1.6
	1.000	1.032	1.091	1.145	1.170

Применив схему Эйткена, найти .

Решение: Записываем данные значения функции в табл. 4.2. и вычисляем разности при.

Таблица 4.2

Схема Эйткена для примера 4.2.

0 1 2 3 4	1,0 1,1 1,3 1,5 1,6	1,000 1,032 1,091 1,145 1.170	-0,15 -0,05 0,15 0,35 0,45	1,048 1,047 1,050 1,057	1,048

Затем последовательно находим:

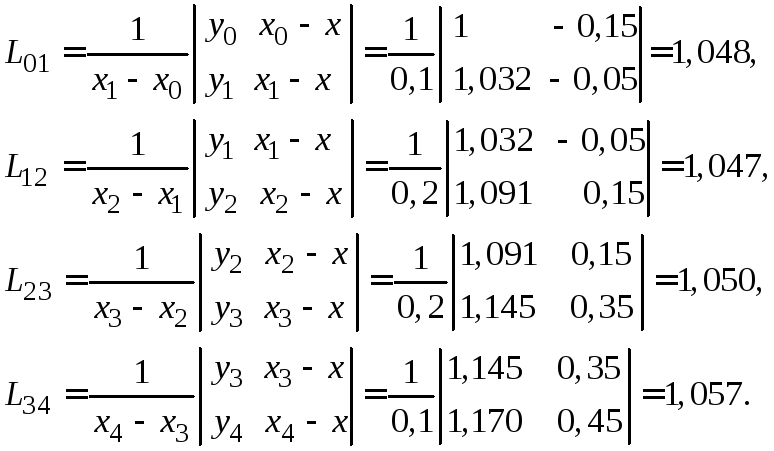
Полученные значения L_i-1 заносим в таблицу, после чего вычисляем

Значения исовпадают до третьего знака. На этом вычисления можно прекратить и с точностью до 10^-3записать

Первая и вторая интерполяционные формулы Ньютона

Часто интерполирование ведется для функций, заданных таблицами с равноотстоящими значениями аргументов. В этом случае шаг таблицы является величиной постоянной.

Составим таблицу конечных разностей, которые вычисляются по формуле:

.

Таблица 4.3

Таблица конечных разностей

				…
…	…	…	…

Первым интерполяционным многочленом Ньютона называется многочлен вида:

(4.6)

Практически формула (4.6) применяется в несколько ином виде. Положим: илиx = x₀ + ht. Тогда в новых обозначениях формула (4.6) перепишется:(4.7)

В выражение многочлена (4.7) входят разности Поэтому формулу (4.7) удобно применить для интерполирования в начале таблицы. Если требуется найти значение функцииf(x)при значенииx = x', то в качествеx₀ берут ближайшее кx', причем меньшее значение аргумента. Говорят, что первый многочлен Ньютона применяется для интерполирования вперед.

Оценка погрешности первой интерполяционной формулы Ньютона:

где . (4.8)

Если аналитическое выражение неизвестно или его трудно вычислить, то можно использовать следующую формулу:

где . (4.9)

Вторым интерполяционным многочленом Ньютона называется многочлен вида:

(4.10)

На практике удобнее пользоваться другой формой записи многочлена:

Положим или. В новых обозначениях получаем:

Оценка погрешности второго интерполяционного многочлена Ньютона:

где . (4.12)

Если аналитическое выражение неизвестно или его нужно вычислить, то можно использовать следующую формулу:

где . (4.13)

В выражение многочлена (4.11) входят разности:

Поэтому формулу (4.11) используют для интерполирования в конце таблицы. Если требуется найти значение функции f (x) при значении x = x’, то в качестве берут ближайшее к x’ (большее) значение аргумента из чисел, содержащихся в таблице.

Говорят, что второй многочлен Ньютона применяется для интерполирования назад.

Рассмотрим пример использования многочленов Ньютона для интерполирования.

Пример 4.3. Функция y = f (x) задана таблицей значений с шагом h.

а) Запишите первый интерполяционный многочлен Ньютона второго порядка, используя указанную ниже таблицу разностей.

0,150 0,155 0,160 0,165 0,170 0,175 0,180	0,14944 0,15438 0,15932 0,16425 0,16918 0,17411 0,17903	494 494 493 493 493 492	0 -1 0 0 -1	-1 1 0 1

Вычислить значения функции при x = 0,156 при помощи первого многочлена Ньютона

Положим:

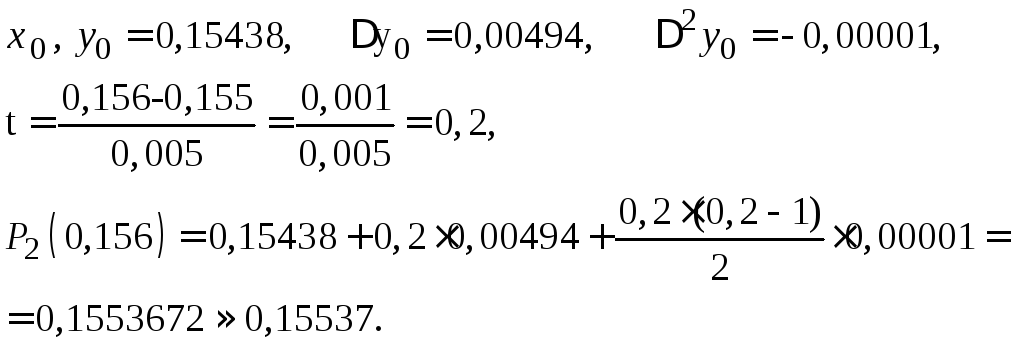
б) Грубую оценку погрешности полученного значения можно получить, используя формулу (4.13).

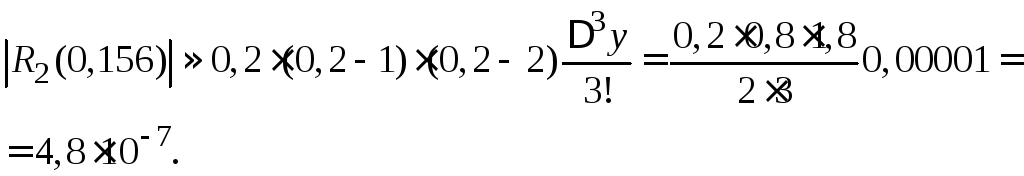
Интерполяция сплайнами.

При большом количестве узлов интерполяции сильно возрастает степень интерполяционных многочленов, что делает их неудобными для вычислений. Высокой степени многочленов можно избежать, разбив отрезок интерполяции на несколько частей с построением на каждой части самостоятельного интерполяционного многочлена. Такое интерполирование приобретает существенный недостаток: в точках стыка разных интерполяционных многочленов будет разрывной их первая производная.

В этом случае удобно пользоваться особым видом кусочно-полиномиальной интерполяции – интерполяцией сплайнами.

Сплайн – это функция, которая на каждом частичном отрезке является алгебраическим многочленом, а на всем заданном отрезке непрерывна вместе с несколькими своими производными. Ниже рассмотрен способ построения сплайнов третьей степени (кубических сплайнов), наиболее распространенных на практике.

Пусть интерполируемая функция задана своими значениямив узлах

На отрезке [] функцию запишем в виде:

(4.14)

где - неизвестные коэффициенты (всего их 4n).

Используя совпадение значений в узлах с табличными значениями функции, получаем следующие уравнения:

(4.15)

(4.16)

Число этих уравнений – 2n. Для получения дополнительных уравнений используем непрерывность и в узлах интерполяции интервала ().

Получаем следующие уравнения:

(4.17)

Для получения еще двух уравнений используем условие – равенство нулю второй производной в точках:

(4.18)

Исключив из полученных выше уравнений, получаем систему, содержащую 3nнеизвестных:

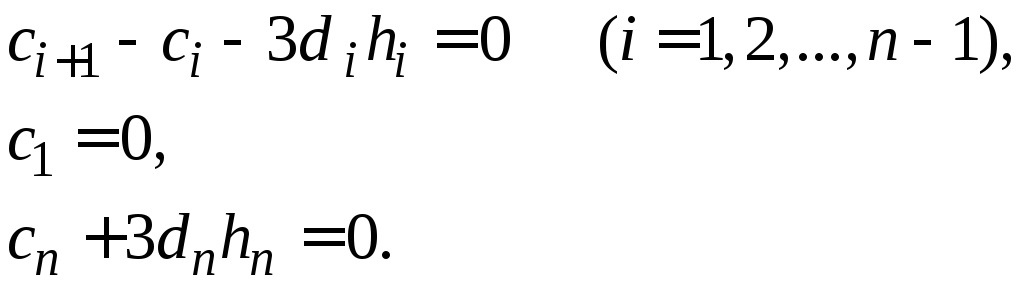(4.19)

Решив данную систему, получаем значения неизвестных , которые определяют сплайн.

Рассмотрим пример построения сплайна.

Пример 4.4. Интерполирующая функция задана таблицей, содержащей четыре узла.

	2	3	4	5
	4	-2	6	-3

Используя формулы (4.14), составляем кубический сплайн:

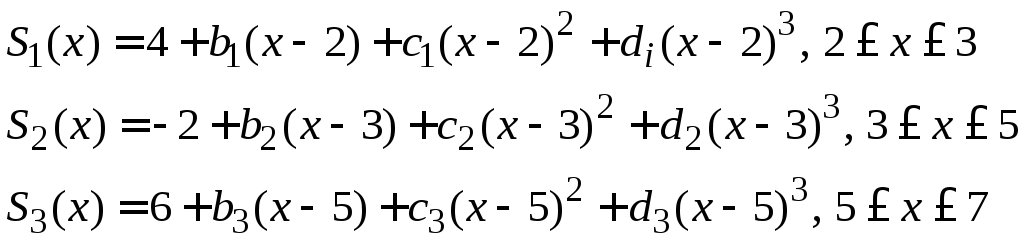
Составляем систему уравнений с использованием формул (4.19):

Коэффициенты системы представлены в таблице 4.4.

Таблица 4.4

Коэффициенты, определяющие матрицу системы примера 4.4

									Своб. члены
1	1	1	0	0	0	0	0	0	-6
0	0	0	2	4	8	0	0	0	8
0	0	0	0	0	0	2	4	8	-9
-1	-2	-3	1	0	0	0	0	0	0
0	0	0	-1	-4	-12	1	0	0	0
0	-1	-3	0	1	0	0	0	0	0
0	0	0	0	-1	-6	0	1	0	0
0	0	1	0	0	0	0	0	0	0
0	0	0	0	0	0	0	1	6	0

Система может быть решена с использованием компьютера, например, методом Гаусса. Получаем решение (результаты округлены до двух знаков после запятой):

Полученные значения коэффициентов определяют искомый сплайн:

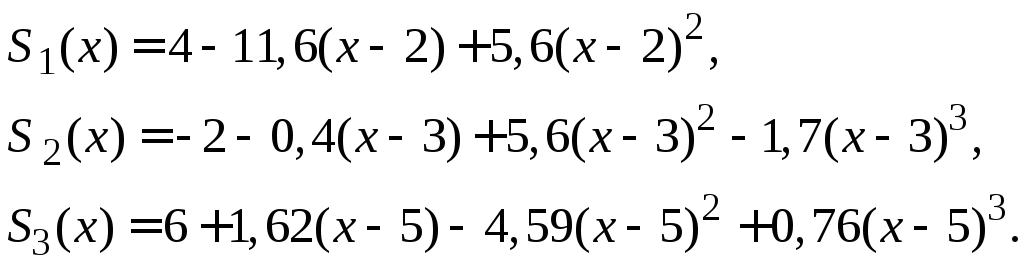
8. Численное решение задачи Коши для дифференциальных уравнений. Методы Эйлера, Рунге–Кутта. Многошаговые методы. Метод прогноза-коррекции.

Постановка задачи Коши

Рассмотрим обыкновенное дифференциальное уравнение первого порядка: . (1.1)

Основная задача, связанная с этим уравнением – задача Коши состоит в следующем: найти решение уравнения (1.1) в виде функции удовлетворяющей начальному условию:. (1.2)

Геометрически это означает, что требуется найти интегральную кривую проходящую через заданную точкупри выполнения равенства (1.1). Существование и единственность решения уравнения (1.1) обеспечивается следующей теоремой.

Теорема Пикара: Если функцияf определена и непрерывна в некоторой областиG, определённой неравенствами:

(1.3)

и удовлетворяет в этой области условию Липшица по у:, то на некотором отрезке, гдеh– положительное число, существует, и притом только одно, решениеуравнения (1.1), удовлетворяющее начальному условию.

Здесь М– постоянная (константа Липшица), зависящая в общем случае ота иb.

Если f(x, y)имеет ограниченную вGпроизводную, то приможно принять.

В классическом анализе разработаны методы нахождения решений дифференциальных уравнений через элементарные (или специальные) функции. На практике эти методы очень часто оказываются либо совсем беспомощными, либо их использование требует трудных вычислений и времени.

Для решения практических задач созданы методы приближённого решения дифференциальных уравнений.

Пусть требуется на отрезке [х₀, х₀₀+Н] найти решение уравнения (1.1) при начальном условии (1.2).

Разобьём отрезок на п равных частей точками: ,где .

Численное решение дифференциального уравнения (1.1) заключается в том, что значение искомой функции вычисляется в каждой точке. При этом, как правило, для вычисления значенияиспользуется уже вычисленное значение.

Для решения задачи Коши для обыкновенных дифференциальных уравнений существуют различные методы:

1. Аналитические методы, применение которых дает решение дифференциального уравнения в виде аналитического выражения.

2. Графические методы, дающие приближенное решение в виде графиков.

3. Численные методы (табличные), при использовании которых искомая функция получается в виде таблицы.

Ниже рассматриваются относящиеся к указанным группам некоторые методы решения обыкновенных дифференциальных уравнений первого порядка вида (1.1).

Метод последовательных приближений

Рассмотрим задачу Коши для дифференциального уравнения первого порядка с начальным условием.

Метод последовательных приближений состоит в том, что решение , получают как предел последовательности функций, которые находятся по рекурсивной формуле

. (1.4)

Если правая часть в некотором замкнутом прямоугольнике, содержащем множество точек, для которых выполняются условияудовлетворяет условию Липшица по:

,

то независимо от выбора начальной функции последовательные приближения сходятся на некотором отрезкек точному решению задачи Коши.

Если непрерывна в области, то оценка погрешности приближенного решения на отрезке дается неравенством:

, (1.5)

где , а число определяется из условия:

.

Пример 1.1. Найти три последовательных приближения решения уравнения:

с начальным условием Оценить погрешность третьего приближения на отрезке.

Решение. Учитывая начальное условие, заменим уравнение интегральным

.

В качестве начального приближения возьмем . Первое приближение находим по формуле (1.4):

.

Аналогично получаем второе и третье приближения:

,

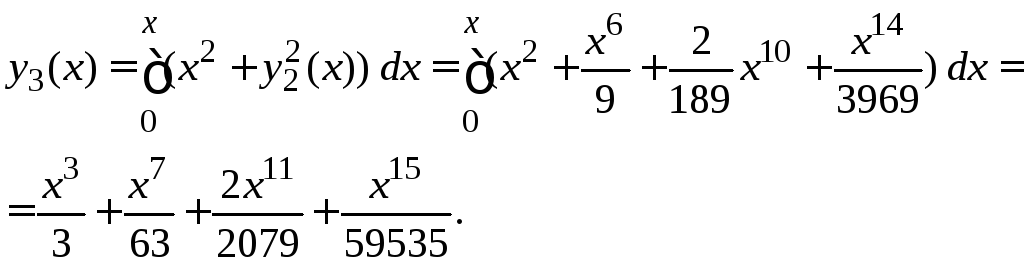
Оценим погрешность последнего приближения по формуле (1.5). Так как функция , то она определена и непрерывна во всей плоскостии в качествеиможно взять любые числа. Возьмем для определенности. При таких ограничениях получаем:

,

.

Таким образом, на отрезке [0; 0.4] получаем

,

и, следовательно:

.

Замечание: Оценка погрешности по формуле (1.5) часто оказывается завышенной. Практически, применяя метод последовательных приближений, вычисления продолжают до такого при котором значениясовпадают в пределах допустимой точности.

Пример 1.2. Дана система

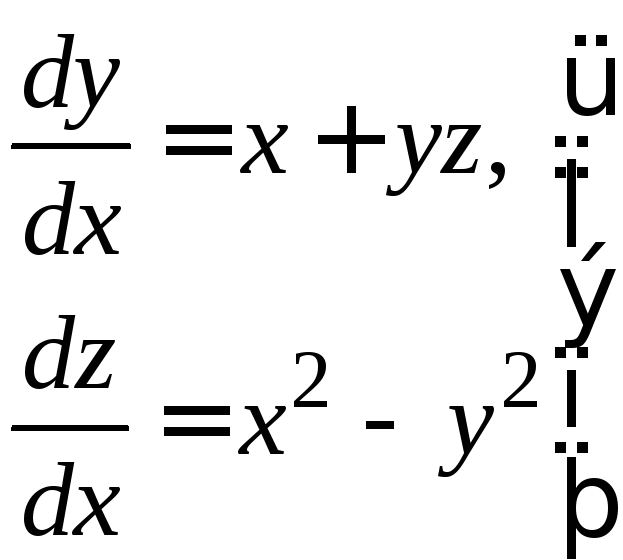
с начальными условиями Методом последовательных приближений найти решение этой системы на отрезке [0; 0,3] с точностью до.

Решение: Записываем систему в интегральной форме:

,

используя начальные значения, из системы находим ,. В качестве начальных приближений выберем:

,

При выборе начальных приближений используем первые два члена разложения функций в окрестности точки

Вычислим следующие приближения и:

,

.

Аналогично получаем:

,

.

Оценим разности ина отрезке [0; 0.3]:

,

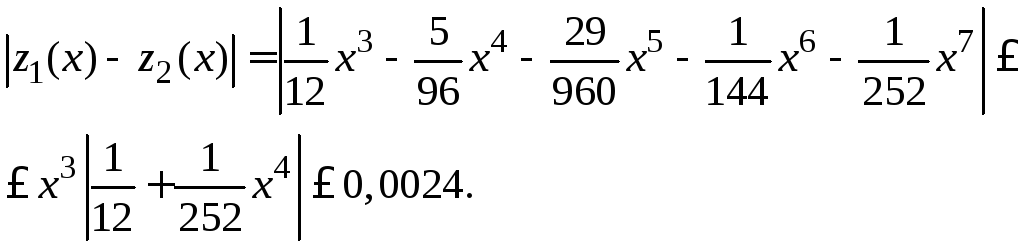
Эти разности находятся в пределах заданной точности, причем члены, содержащие , малы на отрезке [0; 0,3]. Следовательно, с заданной точностью можно положить

,  .

Метод Эйлера

Рассмотрим дифференциальное уравнение с начальным условием.

Выбрав достаточно малый шаг , построим систему равноотстоящих узлов, ().

Приближенные значения по методу Эйлера вычисляются последовательно по формулам:

()

При оценке погрешности обычно используется двойной пересчет.

Если – вычисленное значениес шагом, а– соответствующее узловое значение, полученное с шагомh, то для ориентировочной оценки погрешности последнего значения можно использовать формулу:

Пример 1.3. Применяя метод Эйлера, составить на отрезке [0,1] таблицу значений решения уравнения:

с начальным условием , выбрав шаг.

Решение дифференциального уравнения приведено в таблице 1.1.

Таблица 1.1

Приближенное решение уравнения примера 1.3 методом Эйлера

№ шага				Точное решение
0	0	1,0000	0,2000	1,0000
1	0,2	1,2000	0,1733	1,1832
2	0,4	1,3733	0,1561	1,3416
3	0,6	1,5294	0,1492	1,4832
4	0,8	1,6786	0,1451	1,6124
5	1,0	1,8237		1,7320

Рассмотрим пример вычисления :

.

Для остальных значений вычисления проводятся аналогично.

Метод Эйлера–Коши

Метод Эйлера–Коши является модификацией метода Эйлера. Вычисления табличных значений решения и оценка погрешности проводятся по следующим формулам.

,

,

,

где – точное значение решения в узле,,– приближенные значения решения в узлес шагом– соответственно.

Таблица 1.2

Приближенное решение уравнения примера 1.3 методом Эйлера–Коши

№ шага				Точное решение
0	0	1,0000	0,1867	1,0000
1	0,2	1,1867	0,1617	1,1832
2	0,4	1,3484	0,1454	1,3416
3	0,6	1,4938	0,1341	1,4832
4	0,8	1,6272	0,1263	1,6124
5	1,0	1,7542		1,7320

Рассмотрим применение метода Эйлера–Коши для примера 1.3, решенного выше методом Эйлера.

Покажем пример вычисления :

, .

Остальные значения проводятся аналогично. Результаты счета приведены в таблице 1.2.

Метод Рунге–Кутта четвертого порядка

Рассмотрим метод Рунге–Кутта четвёртого порядка для нахождения численного решения уравнения (1.1) с начальным условием (1.2).

Пусть является начальным условием (при), либо получено как результат предыдущего шага. Для получения следующего значениявначале вычисляются числа:

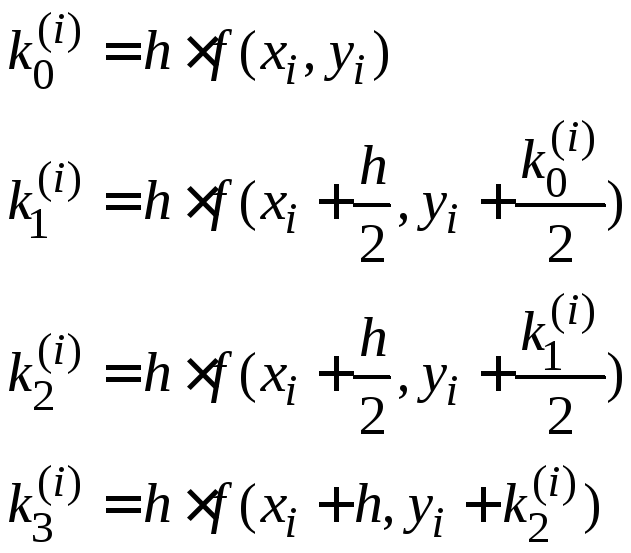, (1.6)

где h– шаг интегрирования.

Затем вычисляют: .

Новое значение функции вычисляется по формуле:

. (1.7)

Метод Рунге–Кутта четвертого порядка является методом повышенной точности. На практике для контроля точности этого метода используется двойной счет пересчет.

Если – вычисленное значениес шагом, а– соответствующее узловое значение, полученное с шагомh, то для приближенной оценки погрешности значенияможно использовать формулу:

.

Пример 1.4. Решить методом Рунге–Кутта уравнение на отрезке [0, 1] с шагом h = 0,2:

.

Результаты вычислений оформим в виде таблицы 1.3.

Таблица 1.3

Результаты приближенного решения примера 1.4 методом Рунге–Кутта

четвертого порядка

0	0,0	1,0000	0,2000	0,1980	0,2000	0,1916	0,1972
1	0,2	1,1972	0,1916	0,1810	0,4000	0,1653	0,1799
2	0,4	1,3771	0,1653	0,1460	0,6000	0,1218	0,1448
3	0,6	1,5219	0,1217	0,0950	0,8000	0,0646	0,0941
4	0,8	1,6160	0,0646	0,0330	1,0000	0,0000	0,0326
5	1,0	1,6486

Покажем пример вычисления табличного значения .

Для вычисления надо вычислить:

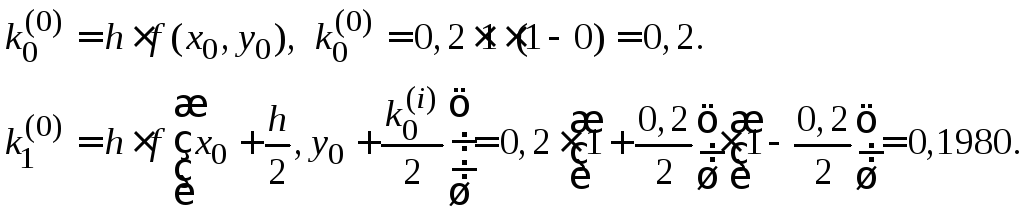
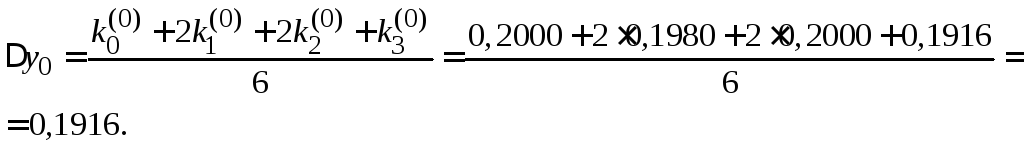
Остальные значения вычисляются аналогично.

Многошаговые методы. Метод Адамса. Методы прогноза–коррекции

В многошаговых методах для вычисления требуется не одно предыдущее значение, а несколько. Так, дляk-шагового метода требуются значения:.

Метод Адамса является примером многошаговых методов решения обыкновенных дифференциальных уравнений. Простейший случай метода Адамса получается при и совпадает с рассмотренным ранее методом Эйлера первого порядка. В практических расчетах чаще используется метод Адамса, имеющий четвертый порядок точности и использующий на каждом шаге результаты предыдущих четырех значений приближенного решения. Именно этот метод называют обычно методом Адамса. Рассмотрим расчетные формулы для данного метода.

Пусть вычислены значения в четырех последовательных узлах . Формула для вычисления значенияпо методу Адамса имеет вид:

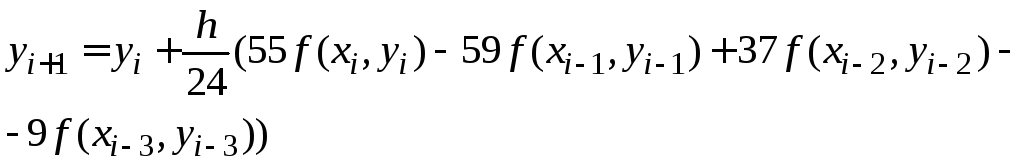. (1.8)

Первые четыре значения для начала вычисления значений решения по методу Адамса получаются любым другим методом соответствующей точности, например, методом Рунге-Кутта четвертого порядка.

Сравнивая метод Адамса с методом Рунге-Кутта той же точности, следует отметить его экономичность, так как он требует при вычислении лишь одного значения правой части на каждом шаге, а метод Рунге–Кутта – четырех. Но метод Адамса неудобен тем, что невозможно начать счет только по известному значению , надо вычислить ещекаким-либо другим способом (например, методом Рунге–Кутта), что существенно усложняет алгоритм. Кроме того, метод Адамса не позволяет (без усложнения формул) изменить шагh в процессе счета.

Существует еще одно семейство многошаговых методов, которые используют неявные схемы, - методы прогноза и коррекции. Суть этих методов состоит в следующем.

На каждом шаге вводятся два этапа, использующих многошаговые методы:

1) с помощью явного метода (прогноза) по известным значениям функции в предыдущих узлах находятся начальное приближение в новом узле;

2) используя неявный метод (корректор), в результате итераций находятся приближения

Один из вариантов метода прогноза и коррекции может быть получен на основе метода Адамса четвертого порядка. Для этого используются следующие расчетные формулы.

На этапе прогноза используется рассмотренная выше формула (1.8), а на этапе коррекции:

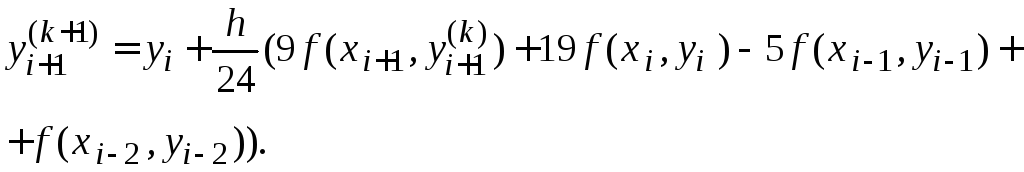(1.9)

Явная схема (1.8) используется на каждом шаге один раз, а с помощью неявной схемы (1.9) строится итерационный процесс вычисления .

Итерации можно прекратить, если две последовательные итерации дают практически одинаковые результаты. На практике, если метод k -шаговый, то итераций должно быть не болееk. Дальнейшее увеличение числа итераций порядок точности не увеличивает. Если точность мала, то надо менять шаг, что в многошаговых методах затруднительно.

Постановка краевой задачи для  обыкновенного  дифференциального уравнения

Пусть дано дифференциальное уравнение второго порядка

(1.10)

Двухточечная краевая задача для уравнения (1.10) ставится следующим образом.

Найти функцию , которая внутри отрезкаудовлетворяет уравнению (110), а на концах отрезка — краевым условиям

(1.11)

Рассмотрим случай, когда уравнение (1.10) и граничные условия (1.11) линейны. В этом случае дифференциальное уравнение и краевые условия записываются так:

	(1.12)
	(1.13)

где – известные непрерывные на отрезкефункции,– заданные постоянные, причеми.

Приближенное решение обыкновенных дифференциальных уравнений методом конечных разностей

Данный метод заключается в следующем.

Разбиваем отрезок наnравных частей с шагоми получаем точки, в которых требуется найти искомые значения.

Введем обозначения:

Заменим приближенно в каждом внутреннем узле производные конечно-разностными схемами:

(1.14)

а на концах отрезка положим:

(1.15)

Используя формулы (1.14)–(1.15), приближенно заменим уравнения (1.12)-(1.13) системой уравнений:

(1.16)

Получим линейную алгебраическую систему, содержащую n+1 уравнение сn+1 неизвестным. Решив данную систему, получаем таблицу приближенных значений искомой функции.

Более точные формулы получаются, если заменить центрально-разностными отношениями:

(1.17)

а на концах отрезка положить:

(1.18)

Используя эти формулы, приближенно заменим уравнения (1.12)–(1.13) системой уравнений:

(1.19)

Пример 1.5. Методом конечных разностей найти решение краевой задачи:

(1.20)

Решение: Используя формулы (1.17), заменяем уравнение (1.20) системой конечно-разностных уравнений

В результате приведения подобных членов получаем

.

(1.21)

Выберем шаг h, равный 0,1. Тогда получим три внутренних узла. Написав уравнение (1.21) для каждого из этих узлов, получим систему:

(1.22)

В граничных узлах имеем: .

Используя эти значения, решаем систему (1.22) и получаем:

.

Для сравнения приведем значения точного решения уравнения (1.18) в  соответствующих точках:.

Приближенное решение обыкновенных дифференциальных уравнений методом прогонки

При большом n непосредственное решение системы (1.16) становится громоздким. Поэтому были разработаны различные методы решения систем такого вида, например, метод прогонки.

Рассмотрим систему (1.16). Метод прогонки решения системы заключается в следующем.

Запишем уравнения системы (1.14) в виде:

,

где

(1.23)

Полученную систему приводим к виду:

(1.24)

Числа последовательно вычисляются по формулам:

при

(1.25)

При

(1.26)

Вычисления производятся в следующем порядке.

Прямой ход. По формулам (1.23) вычисляем значения. Находимпо формулам (1.25). Затем вычисляемпо формулам (1.26) для

Обратный ход. Из уравнения (1.24) прии последнего уравнения системы (1.16) получаем:

Решив эту систему относительно , будем иметь

(1.27)

Используя уже известные числа , находим. Затем вычисляем значения, последовательно применяя рекуррентные формулы (1.22):

(1.28)

Значение находим из предпоследнего уравнения системы (1.16):

(1.29)

Таким образом, все вычисления «прогоняются» два раза.

Вычисления прямого хода заготавливают вспомогательные числа в порядке возрастания индекса. При этом для вычисления значенийиспользуется краевое условие на левом конце отрезка интегрирования. Затем на первом шаге обратного хода происходит согласование полученных чиселс краевым условием на правом конце отрезка интегрирования, после чего последовательно получаются значения искомой функциив порядке убывания индекса.

9. Краевые задачи для обыкновенных дифференциальных уравнений. Методы конечных разностей. Метод прогонки.

Постановка краевой задачи для  обыкновенного  дифференциального уравнения

Пусть дано дифференциальное уравнение второго порядка

(1.10)

Двухточечная краевая задача для уравнения (1.10) ставится следующим образом.

Найти функцию , которая внутри отрезкаудовлетворяет уравнению (110), а на концах отрезка — краевым условиям

(1.11)

Рассмотрим случай, когда уравнение (1.10) и граничные условия (1.11) линейны. В этом случае дифференциальное уравнение и краевые условия записываются так:

	(1.12)
	(1.13)

где – известные непрерывные на отрезкефункции,– заданные постоянные, причеми.

Приближенное решение обыкновенных дифференциальных уравнений методом конечных разностей

Данный метод заключается в следующем.

Разбиваем отрезок наnравных частей с шагоми получаем точки, в которых требуется найти искомые значения.

Введем обозначения:

Заменим приближенно в каждом внутреннем узле производные конечно-разностными схемами:

(1.14)

а на концах отрезка положим:

(1.15)

Используя формулы (1.14)–(1.15), приближенно заменим уравнения (1.12)-(1.13) системой уравнений:

(1.16)

Получим линейную алгебраическую систему, содержащую n+1 уравнение сn+1 неизвестным. Решив данную систему, получаем таблицу приближенных значений искомой функции.

Более точные формулы получаются, если заменить центрально-разностными отношениями:

(1.17)

а на концах отрезка положить:

(1.18)

Используя эти формулы, приближенно заменим уравнения (1.12)–(1.13) системой уравнений:

(1.19)

Пример 1.5. Методом конечных разностей найти решение краевой задачи:

(1.20)

Решение: Используя формулы (1.17), заменяем уравнение (1.20) системой конечно-разностных уравнений

В результате приведения подобных членов получаем

.

(1.21)

Выберем шаг h, равный 0,1. Тогда получим три внутренних узла. Написав уравнение (1.21) для каждого из этих узлов, получим систему:

(1.22)

В граничных узлах имеем: .

Используя эти значения, решаем систему (1.22) и получаем:.

Для сравнения приведем значения точного решения уравнения (1.18) в  соответствующих точках:.

Приближенное решение обыкновенных дифференциальных уравнений методом прогонки

При большом n непосредственное решение системы (1.16) становится громоздким. Поэтому были разработаны различные методы решения систем такого вида, например, метод прогонки.

Рассмотрим систему (1.16). Метод прогонки решения системы заключается в следующем.

Запишем уравнения системы (1.14) в виде:, где

(1.23)

Полученную систему приводим к виду:

(1.24)

Числа последовательно вычисляются по формулам:

при

(1.25)

При

(1.26)

Вычисления производятся в следующем порядке.

Прямой ход. По формулам (1.23) вычисляем значения. Находимпо формулам (1.25). Затем вычисляемпо формулам (1.26) для

Обратный ход. Из уравнения (1.24) прии последнего уравнения системы (1.16) получаем:

Решив эту систему относительно , будем иметь

(1.27)

Используя уже известные числа , находим. Затем вычисляем значения, последовательно применяя рекуррентные формулы (1.22):

(1.28)

Значение находим из предпоследнего уравнения системы (1.16):

(1.29)

Таким образом, все вычисления «прогоняются» два раза.

Вычисления прямого хода заготавливают вспомогательные числа в порядке возрастания индекса. При этом для вычисления значенийиспользуется краевое условие на левом конце отрезка интегрирования. Затем на первом шаге обратного хода происходит согласование полученных чиселс краевым условием на правом конце отрезка интегрирования, после чего последовательно получаются значения искомой функциив порядке убывания индекса.

10. Численные методы решения уравнений с частными производными. Метод сеток. Итерационный метод решения системы конечно-разностных уравнений

11. Методы обработки экспериментальных данных. Подбор эмпирических формул. Определение параметров эмпирической зависимости. Метод наименьших квадратов. Метод наименьших квадратов.

12. Методы оптимизации. Основные понятия. Задачи с ограничениями. Линейное программирование. Геометрический метод. Симплекс–метод. Симплекс-таблицы. Задача о ресурсах.

13. Комбинаторные объекты и комбинаторные числа. Размещения. Перестановки. Подмножества множества, множества с повторениями. k-элементные подмножества, биномиальные коэффициенты. Разбиение множества. Числа Стирлинга второго и первого рода. Свойства комбинаторных чисел.

Комбинаторный анализ занимается изучением объектов из конечного мн-ва Е = {а1,а2,…,аn}, эл-тами аi и их св-вами.

Этими объектами моб подмн-ва мн-ва Е, подмн-ва мн-ва Е с опред св-вами. Напр., с повтор-мися или упоряд. эл-тами.

Задачи типа перечислить объекты с заданными св-вами и определить их кол-во.

Мн-во всех подмн-в мн-ва Е — Сигма_n.

Сигма_3 = {пустое мн-во,{a1},{a2},{a3},{a1,a2},{a1,a3},{a2,a3},{a1,a2,a3}}.

Размещения

Размещением эл-тов из Е по к называется упорядоченное(!) подмн-во из k эл-тов, принадлежащее мн-ву Е.

(A^k)_n — число возможных размещений, к-рые -~ построить из E/

----------

число всех возможных способов разместить k предметов по n ящикам, не более чем по одному в ящик, называется числом размещений без повторений;

с повторениями U(m,n) = m^n.

---------

(A^k)_n = n!/(n-k)!

----------

(A^k)_n = 0 при k > n;

(A^0)_n = (A^0)_0 = 1.

----------

Существуют рекуррентные соотношения:

(A^k)_n = n*(A^(k-1))_(n-1);

(A^k)_n = (A^(k-1))_n * (n-k+1);

[/доказать по св-вам факториала\]

Перестановки

Перестановки — частный случай размещения эл-тов из мн-ва E.

Перестановки — упорядоченные подмн-ва из n эл-тов мн-ва Е = {a1,a2,…,an}.

Pn — число перестановок из мн-ва Е

Pn = (A^n)_n = n!

Сочетания

Сочетание из мн-ва Е по k называется неупорядоченное подмн-во из k эл-тов, принадлежащих мн-ву Е.

(C^k)_n = n!/(k!(n-k)!)

[/т.к. k! повторений, это легко понять\]

--------

В записи (C^k)_n C -~ опускать, в скобках пишут n сверху, а k — снизу.

(0,0) = (n,0) = (n,n) = 1;

(n,k) = (n,n-k);

(n,i)*(i,r) = (n,r)*(n-r,i-r) при 0<=r<=i<=n;

(n,k) = (n-1,k) + (n-1,k-1);

(n,k) = 0 при k > n.

[/доказать по св-вам факториала\]

[/Построить таблицу (n,k), юзая треугольние Паскаля\]

--------

Бином Ньютона

(1+x)^n = SUM[k=0..n]((C^k)_n * x^k);

(a+b)^n = SUM[k=0..n]((C^k)_n * a^k * b^(n-k));

--------

Сочетания с повторениями из A по k — неупорядоченный набор из k эл-тов, в к-ром эл-ты -~ повторяться и любой эл-т сочетания встречается в A.

(H^k)_n = (C^k)_(n+k-1).

-P:

Пусть a’ — произвольное сочетание с повторяющимися эл-тами из A по k эл-тов. Данному сочетанию поставим в соответствие набор 0 и 1 длины n+k-1. Длина — число 0 и 1, заданных в наборе. Набор содержит n-1 нулей и k единиц.

В данном наборе нули отделяют единицы, число к-рых указывает, сколько эл-тов ai входит в сочетание a’.

Данное соответствие му сочетаниями с повторениями и наборами a’ взаимно однозначно, но число взаимных наборов длины n+k-1, содержащих n-1 нулей и k единиц = числу сочетаний (C^k)_(n+k-1).

Стирлинга II

E={a1,a2,..,an}.

|E|=n, n>0.

K — число разбиений мн-ва Е на непустые подмн-ва.

Ф(n,k) — число разбиений мн-ва Е на k непустых частей (0<k<=n).

Ф(n,k) — числа Стирлинга II-го рода.

--------

Ф(4,2) = 7:

{1,2,3}{4}

{1,2,4}{3}

{1,3,4}{2}

{2,3,4}{1}

{1,2}{3,4}

{1,3}{2,4}

{1,4}{2,3}

--------

Ф(0,0)=1

Ф(n,0)=0 при n>0

Ф(n,n)=1

Ф(n,k)=0 при k>n

--------

Ф(n,k) = Ф(n-1,k-1) + k*Ф(n-1,k),

0<k<n

1) Ф(n-1,k-1) — те, которые получаются, когда k-ый элемент состоит в отдельном мн-ве;

2) + k*Ф(n-1,k), т.к. -~ добавить k-ый элемент поочерёдно во все блоки мн-ва {1,2,..n-1}, к-рое нужно разбить на k блоков.

--------

Рассмотрим мн-во многочленов вида

1,х,x^2,…,x^k.

Pk(x) = SUM(i=0..k)(ai*x^i).

{x^i} — базис в пр-ве многочленов.

1,x,x(x-1),x(x-1)(x-2),…,x(x-1)*…*(x-k+1).

[x]_i = x(x-1)*…*(x-i+1).

{[x]_i} — базис в пр-ве многочленов.

Pk(x) = SUM(i=0..k)(ai*x^i).

Pk(x) = SUM(i=0..k)(ci*[x]_i).

x^n = SUM(k=0..n)(Ф(n,k) * [x]_k)

Стирлинга I

-~ поставить обратную задачу. Разложить элемент [x]n на SUM(k=0..n)(C_k * x^k)

[x]_n = SUM(k=0..n)(C_k * x^k)

C_k - числа Стирлинга I рода.

[x]_n = SUM(k=0..n)( фи(n,k) * x^k )

фи(n,k) — обозначение чисел Стирлинга I рода.

14. Рекуррентные соотношения. Возвратные последовательности. Производящие функции. Принцип включения и исключения.

Рек соотнош-я

Последовательность называют возвратной степени k, если для некоторого k и всех n выполняется:

A_(n+k) + pi*a_(n+k-1) + … + pk*an = 0 (*1*).

pi (i=1..k) = const

aj — элемент последовательности.

Такая возвратная последовательность характеризуется следующим многочленом (характеристическим):

P(x) = x^k + p1*x^(k-1) + … + pk.

Для решения (*1*) используем корни многочлена.

Сформулируем следующее утверждения (св-ва возвратной последовательности):

1) если лямбда является корнем характеристического многочлена, то последовательность лямбда^n удовлетворяет (*1*), -~ проверить подстановкой;

2) если лямбда1, лямбда2,…,лямбдаk — простые корни характеристического многочлена, то общее решение (*1*) представимо в виде:

an = c1*(лямбда1)^n + c2*(лямбда2)^n + … + ck*(лямбдаk)^n, где ci = const;

3) Рассмотрим случай, когда корни хар. мн-на — кратные:

лямбда1, лямбда2,…,лямбдаs — корни хар. мн-на соответствующей кратности r1,r2,…,rs.

Тогда общее решение (*1*) примет вид:

an = SUM(i=1..s)( (c_(i,1) + c_(i,2)*n + … + c_(i,r_i)*n^(r_i - 1) * (лямбдаi)^n).

Проверить, что выр-е an в условиях (2) и (3) является решением (*1*) -~ непосредственной подстановкой в (*1*).

--------

Задачи:

Найти общее решение рекуррентного соотношения:

1)

a_(n+2) – 4*a(n+1) + 3*an = 0.

k=2

P(x) = x^2-4x+3.

Простое решение:

{x1 = 3

{x2 = 1

Общее:

an = c1*3^n + c2*1^n.

=> an = c1*3^n + c2.

2)

a_(n+3) + 10*a_(n+2) + 32*a_(n+1) + 32*an = 0.

k = 3

P(x) = x^3 + 10*x^2 + 32x + 32.

Простые корни: -4;-4;-2.

Общее решение:

=> an = c1*(-2)^n + (c2+c3*n)*(-4)^n.

3)

an = ? по рекуррентным соотношениям и начальным условиям

a_(n+2) – an = 0;

a0 = 0;

a1 = 2.

k = 2.

P(x) = x^2 + 1.

Простые корни: x1 = 1; x2 = -1.

an = c1*(-1)^n + c2*1^n = c1*(-1)^n + c2.

n = 0:

c1 + c2 = 0.

n = 1:

-c1 + c2 = 2.

{c1 + c2 = 0

{-c1 + c2 = 2

{c2 = 1

{c1 = -1

=>

an = (-1)^(n+1) + 1.

15. Булевы функции. Табличное задание булевых функций. Элементарные булевы функции. Простейшие эквивалентности. Принцип двойственности. Полнота систем булевых функций. Представление булевых функций полиномами Жегалкина.

В теории дискретных функциональных систем булевой функцией называют функцию типа , где—булево множество, а n — неотрицательное целое число, которое называют арностью или местностью функции. Элементы 1 (единица) и 0 (ноль) стандартно интерпретируют как истину и ложь, хотя в общем случае их смысл может быть любым. Элементы называютбулевыми векторами. В случае n = 0 булева функция превращается в булеву константу.

Основные сведения. Каждая булева функция арности n полностью определяется заданием своих значений на своей области определения, то есть на всех булевых векторах длины n. Число таких векторов равно 2ⁿ. Поскольку на каждом векторе функция может принимать значение либо 0, либо 1, количество всех n-арных булевых функций равно . То, что каждая булева функция задаётся конечным массивом данных, позволяет представлять их в виде таблиц. Такие таблицы носят названиетаблиц истинности и в общем случае имеют вид:

x1	x2	...	xn	f(x1,x2,...,xn)
0	0	...	0	f(0,0,...,0)
1	0	...	0	f(1,0,...,0)
0	1	...	0	f(0,1,...,0)
1	1	...	0	f(1,1,...,0)
0	1	...	1	f(0,1,...,1)
1	1	...	1	f(1,1,...,1)

Практически все булевы функции малых арностей (0, 1 и 2) сложились исторически и имеют конкретные имена. Если значение функции не зависит от одной из переменных(т.е. строго говоря для любых двух булевых векторов, отличающихся лишь в значении этой переменной, значение функции на них совпадает), то эта переменная называется несущественной.

Нульарные функции. При n = 0 количество булевых функций сводится к двум, первая из них тождественно равна 0, а вторая 1. Их называют булевыми константами.

Унарные функции. При n = 1 число булевых функций равно . Им соответствуют следующие таблицы истинности.

x	g1 ()	g2 (=)	g3 (1)	g4 (0)
0	1	0	1	0
1	0	1	1	0

Здесь:

• g₁(x) — отрицание (обозначения:),

• g₂(x) — тождественная функция,

• g₃(x) иg₄(x) — соответственно, тождественная истина и тождественная ложь.

Бинарные функции. При n = 2 число булевых функций равно . Им соответствуют следующие таблицы истинности.

x	y		f1 ()	f2 ()	f3 ()	f4 ()	f5 ()	f6 ()	f7 ()	f8 ( )
0	0		0	0	1	0	1	1	1	1
0	1		0	1	0	1	0	1	0	1
1	0		0	1	0	1	1	0	0	1
1	1		1	1	1	0	1	1	0	0
x	y		f9	f10	f11	f12	f13	f14	f15	f16
0	0		0	0	1	1	0	0	1	0
0	1		0	1	1	0	0	1	1	0
1	0		1	0	0	1	1	0	1	0
1	1		0	0	0	0	1	1	1	0

Здесь:

• f₁(x, y) —конъюнкция(обозначения: x&y,),

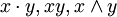• f₂(x, y) —дизъюнкция(обозначение:),

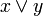• f₃(x, y) —эквивалентность(обозначения:),

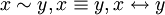• f₄(x, y) —исключающее «или»(сложение по модулю 2; обозначения:),

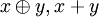• f₅(x, y) —импликацияот y к x (обозначения:),

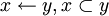• f₆(x, y) —импликацияот x к y (обозначения:),

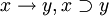• f₇(x, y) —стрелка Пи́рса(функция Да́ггера, функция Ве́бба, антидизъюнкция; обозначение:),

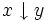• f₈(x, y) —штрих Ше́ффера(антиконъюнкция; обозначение:),

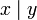• f₉(x, y) — отрицание импликацииf₆(x, y),

• f₁₀(x, y) — отрицание импликацииf₅(x, y),

• f₁₁(x, y) =g₁(x),

• f₁₂(x, y) =g₁(y),

• f₁₃(x, y) =g₂(x),

• f₁₄(x, y) =g₂(y),

• f₁₅(x, y),f₁₆(x, y) — тождественная истина и тождественная ложь.

Полные системы булевых функций

Суперпозиция и замкнутые классы функций. Результат вычисления булевой функции может быть использован в качестве одного из агрументов другой функции. Результат такой операции суперпозиции можно рассматривать как новую булеву функцию со своей таблицей истинности. Например, функции (суперпозиция конъюнкции, дизъюнкции и двух отрицаний) будет соответствовать следующая таблица:

x	y	z		f(x,y,z)
0	0	0		1
0	0	1		1
0	1	0		1
0	1	1		1
1	0	0		0
1	0	1		0
1	1	0		1
1	1	1		0

Говорят, что множество функций замкнуто относительно операции суперпозиции, если любая суперпозиция функций из данного множества тоже входит в это же множество. Замкнутые множества функций называют также замкнутыми классами.

В качестве простейших примеров замкнутых классов булевых функций можно назвать множество {x}, состоящее из одной тождественной функции, или множество {0}, все функции из которого тождественно равны нулю вне зависимости от своих аргументов. Замкнуты также множество функций и множество всех унарных функций. А вотобъединение замкнутых классов может таковым уже не являться. Например, объединив классы {0} и , мы с помощью суперпозициисможем получить константу 1, которая в исходных классах отсутствовала.

Разумеется, множество P₂ всех возможных булевых функций тоже является замкнутым.

Тождественность и двойственность

Две булевы функции тождественны друг другу, если на любых одинаковых наборах аргументов они принимают равные значения. Тождественность функций f и g можно записать, например, так:

Просмотрев таблицы истинности булевых функций, легко получить такие тождества:

			xy=yx
0x= 0	1x=x

А проверка таблиц, построенных для некоторых суперпозиций, даст следующие результаты:

(законы де Моргана)

(дистрибутивность конъюнкции и дизъюнкции)

Функция называется двойственной функции, если. Легко показать, что в этом равенстве f и g можно поменять местами, то есть функции f и g двойственны друг другу. Из простейших функций двойственны друг другу константы 0 и 1, а из законов де Моргана следует двойственность конъюнкции и дизъюнкции. Тождественная функция, как и функция отрицания, двойственна сама себе.

Если в булевом тождестве заменить каждую функцию на двойственную ей, снова получится верное тождество. В приведённых выше формулах легко найти двойственные друг другу пары.

Полнота системы, критерий Поста

Система булевых функций называется полной, если можно построить их суперпозицию, тождественную любой другой заранее заданной функции. Говорят ещё, что замыкание данной системы совпадает с множеством P₂.

Американский математик Эмиль Пост ввёл в рассмотрение следующие замкнутые классы булевых функций:

• Функции, сохраняющие константу T₀иT₁;

• Самодвойственные функции S;

• Монотонные функции M;

• Линейные функции L.

Им было доказано, что любой замкнутый класс булевых функций, не совпадающий с P₂, целиком содержится в одном из этих пяти так называемых предполных классов, но при этом ни один из пяти не содержится целиком в объединении четырёх других. Таким образом критерий Поста для полноты системы сводится к выяснению, не содержится ли вся эта система целиком в одном из предполных классов. Если для каждого класса в системе найдётся функция, не входящая в него, то такая система будет полной, и с помощью входящих в неё функций можно будет получить любую другую булеву функцию.

Заметим, что существуют функции, не входящие ни в один из классов Поста. Любая такая функция сама по себе образует полную систему. В качестве примеров можно назвать штрих Шеффера или стрелку Пирса.

Представление булевых функций

Теорема Поста открывает путь к представлению булевых функций, синтаксическим способом, который в ряде случаев оказывается намного удобнее чем таблицами истинности. Отправной точкой здесь служит нахождение некоторой полной системы функций . Тогда каждая булева функция сможет быть представлена некоторымтермом в сигнатуре Σ, который в данном случае называют также формулой. Относительно выбраной системы функций полезно знать ответы на следующие вопросы:

• Как построить по данной функции представляющую её формулу?

• Как проверить, что две разные формулы эквивалентны, то есть задают одну и ту же функцию?

  • В частности: существует ли способ приведения произвольной формулы к эквивалентной её каноническойформе, такой что, две формулы эквивалентны тогда и только тогда, когда их канонические формы совпадают?

• Как по данной функции построить представляющую её формулу с теми или иными заданными свойствами (например наименьшего размера), и возможно ли это?

Положительные ответы на эти и другие вопросы существенно увеличивают прикладное значение выбранной системы функций.

Простой конъюнкцией, или конъюнктом, называется конъюнкция некоторого конечного набора переменных, или их отрицаний, причём каждая переменная встречается не более одного раза. Дизъюнктивной нормальной формой или ДНФ называется дизъюнкция простых конъюнкций. Например — является ДНФ.

Совершенной дизъюнктивной нормальной формой, или СДНФ относительно некоторого заданного конечного набора переменных называется такая ДНФ, у которой в каждую конъюнкцию входят все переменные данного набора, причём в одном и том же порядке. Например: .

Легко убедиться, что каждой булевой функции соответствует некоторая ДНФ, и даже СДНФ. Для этого достаточно взять таблицу истинности этой функции и найти все булевы векторы, на которых её значение равно 1. Для каждого такого вектора строится конъюнкция, где. Если взять дизъюнкцию этих конъюнкций, то результатом очевидно будет СДНФ. Поскольку на всех булевых векторах её значения совпадают со значениями исходной функции, она будет СДНФ этой функции. Например, для импликации, результатом будет, что можно упростить до.

Конъюнктивная нормальная форма (КНФ) определяется двойственно к ДНФ. Простой дизъюнкцией или дизъюнктом называется дизъюнкция одной или нескольких переменных или их отрицаний, причём каждая переменная входит в неё не более одного раза. КНФ — это конъюнкция простых дизъюнкций.

Совершенной конъюнктивной нормальной формой (СКНФ), относительно некоторого заданного конечного набора переменных, называется такая КНФ, у которой в каждую дизъюнкцию входят все переменные данного набора, причём в одном и том же порядке. Поскольку (С)КНФ и (С)ДНФ взаимодвойственны, свойства (С)КНФ повторяют все свойства (С)ДНФ, грубо говоря, «с точностью до наоборот».

КНФ может быть преобразована к эквивалентной ей ДНФ, путём раскрытия скобок по правилу:

которое выражает дистрибутивность конъюнкции относительно дизъюнкции. После этого, необходимо в каждой конъюнкции удалить повторяющиеся переменные или их отрицания, а также выбросить из дизъюнкции все конъюнкции, в которых встречается переменная вместе со своим отрицанием. При этом, результатом не обязательно будет СДНФ, даже если исходная КНФ была СКНФ. Точно также, можно всегда перейти от ДНФ к КНФ. Для этого следует использовать правило

выражающее дистрибутивность дизъюнкции относительно конъюнкции. Результат нужно преобразовать способом, описанным выше, заменив слово «конъюнкция» на «дизъюнкция» и наоборот.

Полином Жегалкина это форма представления логической функции с помощью Функции Жегалкина (Исключающее ИЛИ). Для получения полинома Жегалкина следует выполнить следуюющие действия:

1. Получить ДНФ функции

2. Все ИЛИ заменить на Исключающее ИЛИ

3. Во всех термах заменить элементы с отрицанием на конструкцию: («элемент» «исключающее ИЛИ» 1)

4. Раскрыть скобки по правилам алгебры Жегалкина и привести попарно одинаковые термы

16. Минимизация булевых выражений. Разложение булевых выражений по переменным. Дизъюнктивные нормальные формы. Карты Карно. Логические сети.

17. Множества. Операции над множествами. Алгебра множеств. Отображения, отношения, функции. Бинарные отношения. Отношения эквивалентности. Отношение эквивалентности. Отношения порядка.

Мно́жество — один из ключевых объектов математики, в частности, теории множеств.

«Множество есть многое, мыслимое нами как единое» (Г. Кантор). Это не является в полном смысле логическим определением понятия множество, а всего лишь пояснением (ибо определить понятие — значит найти такое родовое понятие, в которое данное понятие входит в качестве вида, но множество — это, пожалуй, самое широкое понятие математики и логики).

Существует два подхода к понятию множества.

Первый — так называемая «наивная теория множеств» (созданная Кантором, см. ниже историю). Дать определение чему-либо — это значит выразить понятие через ранее определенные. При этом должны быть некоторые базовые понятия, которые формально не определены. Множество — как раз одно из таких понятий. В рамках наивной теории множеств множеством считается любой чётко определенный набор объектов (элементов множества). Вольное использование наивной теории множеств приводит к некоторым парадоксам.

Второй — аксиоматическая теория множеств.