
Быстрай Г.П. Термодинамика открытых систем Часть 2 (2006)
.pdf
Термодинамика открытых систем
Глава 4. ТЕРМОДИНАМИКА ЛОКАЛЬНО−НЕРАВНОВЕСНЫХ ПРОЦЕССОВ
ПЕРЕНОСА 4.1. Основные положения
Одной из наиболее последовательных и детально разработанных термодинамических теорий, не опирающихся на принцип локального равновесия является так называемая “расширенная необратимая термодинамика” (РНТ) (см. обзор [25]). В рамках РНТ рассматриваются следующие дифференциальные уравнения для диссипативных потоков релаксационного типа [25]:
q + τ |
T |
∂q |
= −λ T , |
(4.1) |
||||
|
|
∂t |
|
|
|
|
||
j + τ |
D |
∂j = −D C , |
(4.2) |
|||||
|
∂t |
|
|
|
|
|||
p + τϑ |
|
∂p |
|
= −ζ ϑ |
(4.3) |
|||
|
|
|
|
∂t |
|
|
|
|
P + τ2 p |
|
∂P |
ϑ |
• |
|
|||
|
|
= −2ηϑ , |
(4.4) |
|||||
|
∂t |
|||||||
|
|
|
|
|
|
|||
где λ − коэффициент теплопроводности, D − коэффициент диффузии, τT , τD , τϑ , τ2 p − времена релаксации соответствую-
щих диссипативных потоков; P=pδ+Pυ, δ − единичный тензор, p − вязкое давление (1/3 следа тензора P), Pυ−часть тензора P со следом, равным нулю, ζ − объемная вязкость, η − сдвиговая вяз-
•
кость, υ − симметрическая часть градиента скорости. При этом потоки уже не определяются градиентом соответствующего термодинамического потенциала переноса, а являются решениями эволюционных уравнений (4.1) – (4.4). Эти уравнения описывают процессы релаксации диссипативных потоков к своим локальноравновесным значениям. Например, в системе с нулевым градиентом концентрации начальное значение массового потока j0 релаксирует к равновесному значению j=0 по экспоненциальному закону:
65
Термодинамика открытых систем
|
|
|
|
t |
|
|
j(t) = |
j0 |
|
− |
|
||
|
||||||
exp |
τT |
. |
||||
|
|
|
|
|
Уравнение Максвелла-Катанео (4.1) может быть представлено как приближение первого порядка при разложении в ряд Фурье
по τT более общего соотношения: q(t + τT ) = −λ T . Послед-
нее означает, что между тепловым потоком и градиентом температуры существует временной сдвиг, равный времени релаксации. Уравнения (4.1)-(4.4) описывают простейшие случаи одноступенчатой (или одностадийной) релаксации и не учитывают как перекрестных, так и пространственно-нелокальных эффектов.
Учет перекрестных эффектов в приближении РНТ позволяет представить уравнения возмущенного движения в виде
Ji |
+ τi |
dJi |
|
= aie |
|
∂S |
|
+ aii |
∂S |
|
; |
|
|
|||||
|
dt |
∂ξe |
∂ξi |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
J e + τe |
|
dJ e |
|
= aee |
|
∂S |
|
+ aei |
∂S |
|
; |
(4.5) |
||||||
|
dt |
|
|
|
|
|
∂ξi |
|||||||||||
|
|
|
|
|
|
|
∂ξe |
|
|
|
||||||||
здесь τi, τe – время релаксации внутренних и внешних термодинамических потоков. Характерные пространственно-временные масштабы L, h, τe=t0 и τi определяют две характерные скорости
[25]
ϑe = τLe , ϑi = τhi .
Скоростьϑe , представляющая собой отношение макромасштабов
рассматриваемого процесса, характеризует линейную скорость изменения параметров системы, вызванную внешними причинами. Например, это может быть скорость перемещения изотерм при движении источника тепловыделения в теплопроводящей
среде. Отношение микропараметровϑi является внутренней характеристикой самой системы и не зависит от внешних условий. Величина ϑi − скорость распространения возмущений потенциала переноса для внутреннего потока. Например, в газах ха-
66

Термодинамика открытых систем
рактерными микропараметрами среды как для процессов теплопереноса, так и процессов массопереноса, являются средняя длина свободного пробега h и время между двумя последовательны-
ми столкновениями молекул τ. Поэтому ϑi – средняя скорость молекул газа, причем ϑi =3D/h=3a/h (D – коэффициент диффу-
зии), поскольку в газах a=D. В расплавах металлов коэффициент диффузии примеси D~10–9−10–8 м2с–1 значительно меньше коэффициента температуропроводности a~10–5−10–4 м2с–1. В результате скорость распространения концентрационных возмущений ϑD ~1−20 мс–1 много меньше скорости распространения тепло-
вых возмущений ϑT ~10–3– 104 мс–1. В такой системе сначала
устанавливаются локально-равновесные значения потока, обладающего минимальным временем релаксации, а только в последующем – локально-равновесные значения другого потока. При
этом характерное время τD ~h/ ϑD много больше, чем время тепловой релаксации τT ~h/ ϑT . Это означает, что в такой системе, сначала, через время порядкаτT устанавливаются локально– равновесные значения температуры и только через время порядка τD – локально-равновесные значения концентрации. После-
довательная релаксация к тепловому, а лишь затем к диффузионному равновесию может возникнуть в системах со сложной структурой, например, в полимерах и капиллярно-пористых средах.
В результате для локально-неравновесных систем скорость изменения энтропии, объединяющая все внешние и внутренние потоки, также будет зависеть от времени релаксации τr, которое связано с одним из наибольших времен релаксации потоков (с самым длительным лимитирующим процессом):
G + τr |
dG |
= −Je X e + Ji X i +σ. |
(4.6) |
|
dt |
||||
|
|
|
Прежде чем использовать полученное уравнение (4.6), обратимся к уравнению теплопроводности для локально-неравновесных систем.
67
Термодинамика открытых систем
Следует отметить, что для локально-неравновесных систем, описываемых уравнениями возмущенного движения - нестационарными уравнениями Онзагера (4.5) можно также сформулировать теоремы 1-3.
4.2.Гиперболическое уравнение теплопроводности
систочником тепла
Если приближения локального равновесия не выполняются τ<<t0, то этим эффектом, учитывающим время релаксации, пренебречь уже нельзя. В этом случае процесс переноса тепла описывается уравнением гиперболического типа
∂T |
+ τT |
∂2T |
= a 2T + |
W |
, |
(4.7) |
|
∂t |
∂t 2 |
CV ρ |
|||||
|
|
|
|
отличающимся от параболического уравнения теплопроводности наличием второй производной температуры по времени и со-
держащим время релаксации теплового потока τT , здесь
[W ] = Вт/ м3 , [W / Cvρ] = K / c , [ a ] = м2 / c , [λ] = Вт/ мK .
Справедливость данного уравнения теплопроводности также можно доказать в рамках термодинамики неравновесных процессов.
T, K
ϑT
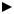 х
х
Рис.4.1. Фронт повышения температуры при отсутствии локального равновесия.
68

Термодинамика открытых систем
Однако, прежде чем это делать, отметим, что уравнение теплопроводности гиперболического вида описывает два семейства характеристик x ± ϑT t = const . Это означает, что тепловой
сигнал (или высокочастотные тепловые возмущения) распространяются в локально-неравновесных условиях с конечной ско-
ростью ϑT =( a / τT )1/ 2 (рис.4.1)[26].
Иными словами, уравнение (4.7) говорит о том, что изменения температуры на поверхности полубесконечного тела будут
распространяться в его объем с конечной скоростью ϑT , в отли-
чие от параболического уравнения теплопроводности. Для уравнения (4.7) можно ввести понятие теплового пограничного слоя
δT ~ ϑT τT = (aτT )1/ 2 − именно на такое расстояние распространится тепловое возмущение за характерное время τT . На фронте
распространяющегося температурного возмущения терпят сильный разрыв не только температура и энтропия, но и свободная
• ••
энергия F, а также ее производные F, F . Это и свидетельству-
ет, что для таких процессов принцип локального равновесия не выполняется.
1. Термодинамическое обоснование гиперболического уравнения теплопроводности. При выводе гиперболического уравнения будем также исходить из закона сохранения энергии для неравновесных систем с источником (1.11). После дифференцирования по времени этого уравнения, имея в виду что
•
J q = Lqq X q − τT J q ,
получаем с учетом (3.3) дифференциальное уравнение сохранения энергии [18] в случае фиксированных потоков:
∂S ∂T |
|
∂ |
2 |
T |
|
|
∂X q |
|
• |
• |
|
|
|
∂σ |
e |
|
|||
+ S |
|
|
=T J |
|
−T |
X |
q |
J |
q |
τ |
T |
+T |
|
,(4.8) |
|||||
∂t ∂t |
|
|
2 |
q ∂t |
∂t |
||||||||||||||
|
∂t |
0 |
0 |
|
|
|
0 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
или −
69
Термодинамика открытых систем
∂T |
|
S + δS ∂2T |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
+ |
=T0 |
λT |
|
− |
|
1 dT |
− |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
∂t |
• |
∂t 2 |
|
|
T 2 |
|
||||||||||
|
|
|
0 |
|
|
|
|
dx |
|
|||||||
|
|
S |
|
|
|
|
|
|
|
0 |
|
|
|
|
||
|
|
|
|
|
|
+T |
|
∂σe |
|
∂t |
. |
|
|
|
|
|
|
|
|
|
|
|
|
∂t |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
0 |
|
∂S |
|
|
|
|
||||
12 d 2T ∂∂t +
T0 dtdx S
Здесь второе слагаемое в правой части (4.8) перенесено в левую часть и оно вошло в структуру второго члена в левой части. Ло- кально-неравновесная энтропия равна S(t)=S+δS, где приращение δS находится из выражения
|
|
• |
|
|
|
|
|
2 |
|
|
|
|
|
|
• |
J q |
|
|
|
|
λ ∂ |
T |
|
|
|
|
|||
δS = T X |
|
τ |
|
= |
|
|
τ |
|
. |
|
||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
2T0 ∂x2 |
|
|
||||||||
0 |
q •• |
T |
|
|
|
T |
|
|
||||||
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, локально-неравновесная |
|
энтропия |
является |
|||||||||||
|
|
|
|
|
|
|
• • |
|
|
|
|
|
|
|
функцией параметров неравновесия X q ,J q , или |
|
|||||||||||||
S( t ) = Seq |
+ |
λτT |
2T |
, |
|
|
(4.9) |
|||||||
|
|
|
||||||||||||
|
|
|
|
|
|
2T0 |
|
|
|
|
|
|
||
здесь [ S ] = Дж / м3K . В результате после деления правой и
•
левой частей уравнения (4.8) на S получаем гиперболическое уравнение теплопроводности (4.7), в котором время релаксации определяется как характеристика изменения энтропии
•
τT = δS / S . В результате источник тепла как и в параболическом уравнении теплопроводности определен в явном виде:
W |
|
|
∂σe |
|
T 2 |
|
∂σe |
|
|||||
|
|
= T |
|
|
|
= |
|
0 |
|
|
|
|
, |
C |
ρ |
∂S |
C |
|
|
∂T |
|||||||
0 |
|
|
|
V |
ρ |
|
|
||||||
|
V |
|
|
|
V |
|
|
|
|
|
V |
|
|
или
W= T02 ∂∂σTe V .
Вслучае независимости источника от температуры из последнего выражения после интегрирования получаем равенство, связы-
70

Термодинамика открытых систем
вающее введенную нами величину σe с интенсивностью внутренних источников тепла
σe = W .
T0
4.3. Термодинамика процессов переноса тепла при отсутствии локального равновесия
Знание пространственно распределенной температуры, которая находится из гиперболического уравнения теплопроводности (4.7), позволяет для локально-неравновесных процессов переноса массы вычислить скорость изменения энтропии, свободной энергии, производство энтропии, которые также зависят от координат и времени. Материал, изложенный в этом параграфе, следует сравнить с изложенным в параграфе 3.2.
1. Скорость изменения энтропии. Скорость изменения энтропии для гиперболического уравнения теплопроводности
(4.7) равна
|
dS |
= σe + J q X q = |
W |
|
λ |
( T )2 − |
λ |
• |
|
+ |
T (T )τT .(4.10) |
||||||
|
|
|
2 |
2 |
||||
|
dt |
|
T0 |
|
|
|||
|
|
T0 |
|
T0 |
|
|||
При этом |
производство энтропии является знакоположительной |
|||||||
функцией. Функция источников в такой задаче также знакоопределена – она знакоположительна. В уравнении (4.10)
[ σe ] = [ σi ] = Дж / м3 Kc .
Второй закон термодинамики применительно к уравнению теплопроводности (4.7) выражается неравенством
σi = J q X q = |
λ |
( T )2 − |
λ |
• |
|
T (T )τT ≥ 0 . |
|||||
T 2 |
T 2 |
||||
0 |
0 |
|
|||
2. Скорость изменения свободной энергии. Скорость изменения свободной энергии для локального объема при суще-
71
Термодинамика открытых систем
ствующем градиенте температуры для уравнения теплопроводности равна
|
|
|
|
|
dF |
= −T ( σe |
+ J |
q |
X |
q |
) , |
|
|
|||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
dt |
0 |
|
|
|
|
|
|||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
• |
|
|
||
|
dF |
|
W |
|
|
λ |
( T )2 − |
λ |
|
|
|
|||||
|
= −T |
+ |
T (T )τ |
, |
||||||||||||
|
|
|
|
|
|
T |
||||||||||
|
dt |
0 |
|
2 |
|
|
|
2 |
|
|
|
|||||
|
|
T0 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
T0 |
|
T0 |
|
|
|
|
||||
здесь температура в трехмерной задаче является функцией времени и координат T =T( x, y,z,t ) , от координат также зависит
|
|
• |
• |
скорость изменение свободной энергииF |
= F( x, y,z,t ) . |
||
|
3. Теорема Пригожина. |
Производство энтропии |
|
( σi |
• |
|
|
= J q X q , J q = Lqq X q − τT J q ) |
при постоянной мощности |
||
теплового источника (W = const ) стремится убывать и принимает минимальное положительное значение в стационарном состоянии в соответствии с термодинамическим уравнением
|
dσ |
i |
|
|
1 |
∂W |
|
1 ∂ |
2 |
F |
|
|
|
• |
|
|||||
|
|
|
= − |
− |
|
, |
|
|
[ F ] = Вт / м3 . |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
dt |
|
|
|
T0 ∂t 2 |
|
|
|
||||||||||||
|
|
|
|
T0 ∂t |
|
|
|
|
|
|
||||||||||
4. Функция Релея (мера рассеивания полной энергии). |
||||||||||||||||||||
При теплопроводности для уравнения (1.21) |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
dΛ |
|
= −2Φ , Λ = ΛF + Λe , |
(3.8) |
||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|||
функция Релея (1.22) примет вид |
|
|
|
|
|
• |
|
|||||||||||||
|
|
T |
|
|
|
|
|
|
|
|
λ |
|
|
|
|
|
λ |
|
||
Φ = |
0 |
|
J q X q = |
|
|
( T )2 |
− |
|
|
J q T τT . |
|
|||||||||
|
|
|
|
2T0 |
|
|||||||||||||||
2 |
|
|
|
|
|
|
2T0 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Здесь Λe термодинамический потенциал внутренних источ-
• •
ников Tσe ≡ Λe , Λe =W а ΛF = F − F0 - термодинамический потенциал (свободная энергия) неравновесного состояния.
72

Термодинамика открытых систем
4. Вариационный принцип. Несложно показать,
что уравнение (3.8), на котором по сути и основан вывод уравнения теплопроводности, тождественно некоторому термодинамическому вариационному принципу
δ Λ• + 2Φ Jq = 0 .
5. Энтропия, свободная энергия для локально-
неравновесных состояний. Как ведет себя свободная энергия для описываемых локалъно-неравновесных состояний с потоками тепла? Она равна в соответствии с (4.9)
F(t) = U0 −T0 S( t ) = F0 − τT a 2T . 2T0
Для процессов, связанных с понижением температуры
•
(T < 0 ), из уравнения теплопроводности (4.7) в самой простой задаче, когда a 2T >>W/Cvρ, τT / ∆t <<1 следует неравенство
a 2T < 0 . Поэтому для таких локально-неравновесных процессов энтропия меньше, а свободная энергия F(t) =U0 −Т0 S(t) больше, чем для локально-равновесных:
S( t ) = S |
eq |
− λτT |
|
2T |
|
, |
F( t ) = F + |
τT a |
|
|
2T |
|
; |
|
|
|
|
||||||||||
|
|
|
|||||||||||
|
2T0 |
|
|
|
|
0 |
2T0 |
|
|
|
|
|
|
|
|
|
F0 = U0 −T 0S0 . |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||
Это и означает, что при низких температурах все |
|
|
равновесные |
||||||||||
системы должны быть так или иначе упорядочены, а свободная энергия для них принимает минимальное значение.
Для процессов, связанных с повышением температуры
•
(T > 0 ) из уравнения теплопроводности для выше указанных
условий следует неравенство a 2T > 0 . Поэтому для таких ло- кально-неравновесных процессов энтропия больше, а свободная энергия F(t) =U0 −Т0 S(t) меньше, чем для локально-
равновесных:
73
|
Термодинамика открытых систем |
|
|
|
|
|
|||||||
S( t ) = S |
eq |
+ λτT |
|
2T |
|
, |
F( t ) = F − |
τT a |
|
|
2T |
|
. |
|
|
|
|
||||||||||
|
|
|
|||||||||||
|
2T0 |
|
|
|
|
0 |
2T0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Это и означает, что при высоких температурах все равновесные системы должны быть упорядочены меньше, чем при низких, свободная энергия принимает при этом максимальное значение.
6. Температура для локально-неравновесных состоя-
ний. Принимая во внимание, что локально-равновесная темпера- |
|||||||
тура T определяется из соотношения T −1 |
= (∂S |
eq |
/ ∂U ) , ло- |
||||
кально-неравновесная температура θ |
0 |
|
V |
||||
может быть найдена из из |
|||||||
(4.9) дифференцированием S(t) по U: |
|
|
|
|
|||
1 = |
1 |
+ |
τT a |
2T . |
|
|
(4.11) |
T0 |
2T 2 |
|
|
||||
θ |
|
|
|
|
|
||
|
|
0 |
|
|
|
|
|
Для процессов, связанных с высокоинтенсивным понижением температуры из уравнения теплопроводности следует
неравенство a 2T < 0 , в результате получаем, что локальнонеравновесное значение температуры θ<T, т.е. меньше чем ло- кально-равновесное:
|
|
T0 |
|
|
• |
|
θ = |
|
|
|
, T |
< 0 . |
|
|
τT a |
|
2T |
|||
1 + |
|
|
|
|||
2T |
|
|||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
Для процессов, связанных с высокоинтенсивным повышением температуры из уравнения теплопроводности следует неравенство a 2T > 0 , в результате получаем, что локальнонеравновесное значение температуры θ>T, т.е. больше чем ло- кально-равновесное:
|
|
T0 |
|
|
• |
|
θ = |
|
|
|
, T > 0 . |
||
1 − |
τT a |
|
2T |
|||
|
|
|
||||
2T |
||||||
|
|
|
|
|
||
|
|
0 |
|
|
|
Следует подчеркнуть [25], что, строго говоря, в уравнении для потока тепла (4.1) должен стоять градиент локальнонеравновесной температуры θ, а не T . Обычно в практиче-
74
Термодинамика открытых систем
ских ситуациях разница между θ и T невелика. Однако с концептуальной точки зрения появление θ в уравнении для теплового потока означает существование локально-неравновесного стационарного состояния q = −λ θ, которое может существенно
отличаться от локально-равновесного стационарного состояния q = −λ T .
На рис.4.2.представлено отношение температуры θ к равновесной при высокоинтенсивных процессах нагрева и охлаж-
дения для фиксированного значения отношения параметра τT к
T0.
1.4
•
T > 0
1.2
θ/T
1
•
T < 0
0.8
0 |
2 .104 |
4 .104 a |
2 T |
|
|
|
K/c |
Рис.4.2. Отношение локально-неравновесной температуры к равновесной при высокоинтенсивных процессах нагрева и охлаждения при τT / T0 =1.25 10−5 .
Отметим, что уравнение теплопроводности гиперболического типа сочетает в себе свойства как параболического уравнения теплопроводности, описывающего чисто диссипативный способ передачи энергии, так и волнового уравнения (вторая производная по времени), описывающего распространение незатухающих волн. Это объясняет экспериментально наблюдаемые
75
Термодинамика открытых систем
волновые свойства процессов теплопереноса при низких температурах – распространение тепловой волны с конечной скоростью [25], отражение тепловой волны от теплоизолированной границы, а при падении на границу раздела двух сред частичное отражение и частичное прохождение в другую среду; интерференция тепловой волны. Описание процессов горения, плавления, кристаллизации и др. также невозможно без привлечения этих представлений.
Задачи к главе 4
Задача 4.1. Считая уравнения (4.5) нестационарными уравнениям переноса в локально неравновесных системах сформулируйте и докажите для них теорему 1 для устойчивых по Ляпунову процессов.
Задача 4.2. Определить производство энтропии и скорость изменения энтропии для локально неравновесных процессов, описываемых гиперболическим уравнением с нелинейным тепловым источником
∂T |
+ τT |
∂2T |
= a 2T +βT − αT 3 , |
∂t |
|
∂t 2 |
|
76
Термодинамика открытых систем
Глава 5. ТЕРМОДИНАМИКА ХАОТИЧЕСКИХ СИСТЕМ
Классическая механика лишила иллюзии, что можно построить вечный двигатель первого рода, термодинамика - второго, квантовая механика - что мы можем одновременно сколь угодно точно измерять координату микрочастицы и ее импульс, теория относительности - что удастся передавать информацию в вакууме со сверхсветовой скоростью [37]. Сегодня нелинейная динамика развеяла иллюзию глобальной предсказуемости: мы не можем предсказать, начиная с какого-то горизонта прогноза, поведение многих достаточно простых систем.
Всвое время работа Лоренца, в которой пожалуй впервые описано возникновение детерминированного хаоса, была опубликована в метеорологическом журнале, но в течение 10 лет она не была замечена. Метеорологи сегодня полагают, что горизонт прогноза для погоды не превышает трех недель. Другими словами, как бы точно не измерялиcь параметры атмосферы, предсказать погоду с помощью имеющихся приборов через три недели в данном месте, вообще говоря, невозможно. Горизонт прогноза для состояния океана эксперты оценивают в месяц.
Сейчас многие специалисты по физике Солнца предполагают, что аналогичная ситуация имеет место с Солнцем. Например, известно такое явление, как минимум Маундера [37], когда
втечение почти 70 лет всплесков солнечной активности не было. И возникает вопрос, можем ли мы предсказать следующий аналогичный минимум? Все это же относится к преблеме глобального потепления или похолодания.
Внелинейной динамике обычно выделяют следующие основные характеристики хаотических движений, которые могут рассматриваться как диагностические [27]:
1.Сложный непериодический характер временной эволюции динамических переменных.
2.Экспоненциальный характер разбегания близких по начальным данным траекторий на аттракторе.
3.Диссипативный характер протекающих процессов, который говорит о сжатии фазового объема.
77
Термодинамика открытых систем
4.Непрерывная зависимость спектральной плотности мощности пульсаций от частоты в конечном диапазоне частот.
5.Специфический характер реакции системы на малое изменение параметров и на внешнее воздействие сигналом малой амплитуды.
6.Конечная или бесконечная последовательность бифуркаций, наблюдаемая при вариации некоторого управляющего параметра системы, в результате которых топологическая структура фазовых траекторий претерпевает ряд (конечный
или бесконечный) изменений, завершающихся рождением странного аттрактора.
Анализ необратимых процессов будет неполным без рассмотрения мелко- и крупномасштабных внутренних флуктуаций, которые всегда присутствуют в реальных системах. При наличии локального неравновесия такие флуктуации могут усиливаться и переводить нелинейную систему в новое стационарное состояние, соответствующее новой структуре. Речь по сути идет о неравновесных фазовых переходах в условиях отсутствия локального равновесия. Это означает, что критерий эволюции системы, устанавливающий направление движения начинает зависеть от флуктуаций, а они не могут не отражать присущие системе нелинейные свойства [15]. Поэтому введение в правую часть уравнений типа (2.5), (2.6) источника случайного шума и изучение получаемых следствий при численных расчетах является малоперспективным, так как сразу возникают вопросы по характеристикам этого шума, которые неизвестны. Можно высказать утверждение, что флуктуации должны содержать сами нелинейные уравнения, которые получены выше, но решения указанных уравнений их не содержат. Поэтому рассмотрим некоторые полезные нелинейные модели, основанные на последних, которые приводят к флуктуационным (хаотическим) режимам. Однако вначале сделаем переход от релаксационных уравнений термодинамики к уравнениям второго порядка для параметра порядка, которые возникают в связи релаксацией термодинамических сил и потоков.
Цель этой главы – показать возможность возникновения детерминированного хаоса в термодинамических системах. Под
78

Термодинамика открытых систем
детерминированным хаосом будем понимать хаос, возникающий в системе нелинейных дифференциальных уравнений, число которых не менее трех. Хаос возникает при некоторых условиях, которые следует определить.
5.1. Переход от релаксационных уравнений локальнонеравновесных систем к уравнениям второго порядка
Для локально-неравновесных систем, в которых необходимо учитывать релаксацию скорости изменения энтропии (4.6) следует решать совместно систему двух динамических уравне-
ний для параметра порядка η(t) η= x* − x*0 и приведенной ско-
рости изменения энтропии G*(t+τr). Последняя является знакопеременной потенциальной функцией и для нее справедливо градиентное уравнение
|
dη |
= − |
∂G* |
, |
|
|
|
|
|
|
(5.1) |
||
|
dt |
∂η |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
G* + τ |
r |
dG* |
= |
1 |
η4 |
+ |
1 |
a*η2 |
+ b*η, |
(5.2) |
|||
dt |
4 |
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|||||
здесь τr≡τr/t0 − время релаксации скорости изменения энтро-
пии, или время релаксации потока одного из самых длительных неравновесных процессов. Параметр порядка ηсвязан с отклонением термодинамического потока x=Ji (или силы Xi) от среднего значения x0 в приведенном виде
η= x − x0 , xc xc
здесь xс=Jiс – некоторый масштаб потока. В системе уравнений
(5.1)-(5.2) уже два параметра порядка η(t) и G* ( t ) .
Дифференцируя (5.2) по η и подставляя полученное выражение в (5.1) получаем дифференциальное уравнение второго порядка для локально-неравновесных систем
∂η |
∂2η |
= f (η,t) , |
∂t |
+ τr ∂t 2 |
|
|
|
79 |
Термодинамика открытых систем
f (η,t) = − |
∂G* |
= −(η |
3 |
* |
η+ b |
* |
) , |
(5.3) |
∂η |
|
+ a |
|
|||||
|
|
|
|
|
|
|
|
где f − обобщенная сила двухямного потенциала G* [19]. Член с τr можно не учитывать когда время релаксации скорости изменения энтропии существенно меньше времени действия внешних сил τr /∆t<<1. Термодинамические уравнения (5.1)-(5.3) характеризуют локально-неравновесные процессы. Следует обратить внимание на то, что в нелинейном уравнении (5.3) сила f, пара-
o |
oo |
метр порядка η, скорость его изменения ηи член |
τr ηопределе- |
ны в один и тот же момент времени t.
Можно рассмотреть частный случай, когда внешняя сила H* изменяется по гармоническому закону. Это означает, что управляющие параметры в (5.3) можно представить в виде
b* = −H * + H *s = −H *0 cosωt ,
H s* = 3x0* − 2x0*3 , |
a* = −3(x0*2 |
−1) ; |
(5.4) |
здесь ω – циклическая частота |
изменения |
H*; |
при t =0 |
H 0* = H * − H s* . Наличие в (5.3) времени релаксации и переход к
ДУ второго порядка является необходимым, но недостаточным условием возникновения хаоса.
5.2. Хаос при внешних гармонических воздействиях в условиях запаздывания
Если следовать [28, 29], то в реальных системах следует учитывать также последействие. Если внешнее воздействие представлено в момент времени t−τ, т.е. обобщенная сила
f = −∂G* / dη задана при последействии в виде f (t − τ) . При
o |
oo |
этом диссипативный η( t ) и инерционный |
τr η( t ) члены опре- |
делены в момент времени t. В результате приходим к уравнению для параметра порядка η с запаздыванием:
80
Термодинамика открытых систем
∂η |
+ τr |
∂2η |
= f (t − τ) , |
(5.5) |
∂t |
∂t 2 |
здесь τ − время последействия. Моделирование последействия в самом простом случае подразумевает разложение силы f(t−τ) в ряд; ограничиваясь двумя слагаемыми представим
|
|
∂f (t) dη |
|
∂f |
|
|
f (t − τ) |
f (t) − τ |
|
|
+ |
|
, |
|
|
|||||
|
|
∂η dt |
|
|
|
|
где |
|
|
∂t |
|
||
|
|
|
|
|
|
|
f (t) = −(η3 + a*η) + H 0* cos ωt . |
(5.6) |
|||||
В системе уравнений (5.1), (5.2) и (5.6) уже три параметра
порядка η(t), G* ( t ) и f(t−τ). В результате вместо уравнения
(5.3) получаем для локально-неравновесных систем с запаздыванием каноническое однородное уравнение второго порядка, содержащее время ретардации (запаздывания), в котором:
oo |
o |
|
τr η+ Γ(t) η+ η3 + a*η = H0`* cos ωt , |
(5.7) |
|
где декремент затухания и амплитуда внешней силы равны соответственно
Γ(t) =1− τ(3η2 + a* ) >0,
H 0`* = H0* (1+ τωtg(ωt)) ;
здесь τ = τ/ t0 − приведенное время ретардации (запаздывания); τr = τr / t0 − приведенное время релаксации скорости изменения энтропии (определяется наибольшим временем релаксации тер-
модинамического потока). Переменный параметр γ = Γ( t ) явля-
τr
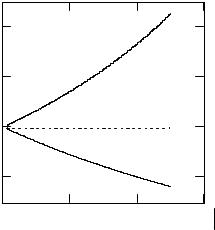
ется параметром диссипации. Численные решения нелинейного уравнения для η (5.7), которое представлялось системой трех нелинейных дифференциальных уравнений, показывают на наличие в широкой области значений управляющих параметров не только регулярных, но и хаотических решений (рис.5.1, рис.5.2).
Как видно из рисунков при некоторых значениях пара-
81
Термодинамика открытых систем
метров в уравнении имеет место как гомо− так и гетерофазный хаос, реализующийся по типу странного аттрактора. В такой нелинейной термодинамической системе параметр порядка “мечется” между двумя симметричными стационарными состояниями (фазами)
η+ =  − a* , η− = −
− a* , η− = − − a* ,
− a* ,
оба из которых являются неустойчивыми. Подставляя хаотические решения в выражение для скорости изменения энтропии G* получаем для этой функции хаотические значения (при a*<0,
рис.5.2).
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Z n , |
1 |
|
|
|
|
|
|
Y0η |
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
− Y0 |
|
|
|
|
|
|
|
− |
2 |
2 |
0 |
50 |
100 |
150 |
200 |
|
|
||||||
|
|
а |
0 |
|
t ( n ) |
t |
200 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
2
η
0
б
2 |
2 |
0 |
2 |
o |
|
||||
|
|
|
|
η |
Рис.5.1. Моделирование гомофазных и гетерофазных флуктуаций внутренней термодинамической силы (а), фазовый портрет (б). а*=−1.5, ω = 2.6 , τ = 0.216 , η(0)=0.3, b0*=1.8. Фа-
зовый портрет соответствует двум аттракторам.
Хаотическую динамику решений уравнения (5.7) можно представить как хаотические колебания в одной из потенциаль-
82

Термодинамика открытых систем
ных ям с перебросом время от времени в другую яму благодаря периодической внешней силе.
Описываемый хаос в термодинамической системе является детерминированным, т.к. решаемое численными методами уравнение не содержит источников шума; он обусловлен нелинейными особенностями уравнения, проявляемых при периодическом воздействии на систему. Хаос означает наличие состояние беспорядка и нерегулярности. Для таких нелинейных систем динамические законы однозначно определяют эволюцию во времени состояния системы при известной предыстории.
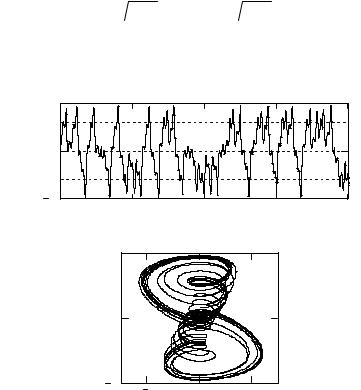
G* |
1 |
|
G* |
1 |
|
|
|
|
|
б |
|||
|
|
а |
|
|
||
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
1 2 |
0 |
η |
1 0 |
50 |
t |
0 
в50
t |
2 |
0 |
η |
|
Рис.5.2. Хаотическая динамика скорости изменения энтропии G* (а,б) и параметра порядка η (в) (см. условия рис.2.2). Положительные значения G* соответствуют устойчивым состояниям по Ляпунову, отрицательные – структурной устойчивости.
83
Термодинамика открытых систем
5.3. Сжатие фазового объема. Диссипативность локально-неравновесной термодинамической системы
Напомним, что если система частиц описывается уравнениями Гамильтона, то при движении частиц фазовый объем остается неизменным. Диссипативные системы обладают той особенностью, что при их движении фазовый объем сжимается. Причем он сжимается к аттрактору более низкой размерности, чем исходное пространство [27, 30]. Покажем, что рассматриваемая нами термодинамическая система, описываемая уравнением (5.7), является диссипативной. Для этого представим ДУ для локально-неравновесной среды в виде автономной системы трех дифференциальных уравнений
o |
|
|
|
|
|
|
|
|
|
|
X = Y , |
|
|
|
|
|
|
|
|
||
o |
|
1 |
|
|
`* |
|
3 |
|
* |
|
Y |
= − |
|
(Γ(X )Y − H 0 |
cos Z + (X |
|
+ a |
|
X )), (5.8) |
||
τr |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
o |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z = ω, |
|
|
|
|
|
|
|
|
||
где |
|
|
|
∂η |
|
|
|
|
|
|
|
|
o |
= |
, Γ(X ) =1− τ (3X 2 + a* ) ; |
||||||
X = η, X |
||||||||||
|
|
|
|
∂t |
|
|
|
|
|
|
H 0`* = H 0* (1+ τω tgZ ) .
Эта система уравнений имеет три степени свободы. Поверхность S, ограничивающая произвольно выбранный в фазовом пространстве {X,Y,Z} фазовый объем V, эволюционизирует так, что каждая ее точка движется по траектории, определяемой системой уравнений (5.8). Отсюда по теореме о дивергенции
dV |
|
o |
|
o |
|
o |
|
|
∂ X |
|
∂Y |
|
∂Z |
||
|
= ∫ |
|
+ |
|
+ |
dXdYdZ , |
|
dt |
∂X |
∂Y |
|||||
|
|
|
∂Z |
||||
|
V |
|
|
|
|
|
или
84
