Быстрай Г.П. Термодинамика открытых систем Часть 2 (2006)

Термодинамика открытых систем

dV	= −∫	Γ( X )	dXdYdZ = −	1	(1− τ ( X 2 + a* ))V ,
dt
	V	τr		τr

Переменный параметр γ = Γ( X ) является параметром диссипа-

τr

ции. Последнее и означает, что элементарный фазовый объем такой диссипативной системы в условиях локального неравновесия сжимается экспоненциально во времени dV / dt < 0 :

			t		2	*
		-		(1− τ ( X				; τ>0,	τr>0, a*<0.
	V(t) =V(0)exp		τr			+ a	))

Система уравнений Лоренца. В качестве аналогичной диссипативной системы можно рассмотреть систему уравнений Лоренца

•

X = −σX + σY ,

•

Y = −XZ + rX −Y ,

•

Z = XY −bZ ,

для которой фазовый объем сжимается во времени: dVdt = −(σ +1+b)V < 0 , (σ > 0,b > 0).

Если ввести новую переменную z =( u + x2 ) / 2σ , то легко показать, что система уравнений

	••	•	x3		xu
	x	+( σ +1) x− σ( r −1)x +		+		= 0 ,
			2		2

•

u = −bu +( 2σ − b )x2

эквивалентна системе уравнений Лоренца. Будем предполагать что u=const. Тогда уравнение второго порядка примет вид

••	•	∂U	,
x	+ γ x = −
		∂x

гдеγ = σ +1 − параметр диссипации. Потенциальная функция для такой задачи имеет вид симметричного двухямного потенциала:

85

Термодинамика открытых систем

U( x ) =	x4	−	( σ( r −1) − u / 2 )x2
					,
	8		2
если коэффициент при		квадратичном		члене положителен

(см.рис.2.2а). Однако u не является параметром, а переменной. Хаотическую динамику системы уравнений Лоренца можно представить как хаотические колебания в одной из потенциальных ям с перебросом время от времени в другую яму благодаря изменению величины u, и, соответственно, формы потенциала.

5.4. Показатели Ляпунова

Наблюдаемое во времени хаотическое поведение возникает не из-за внешних источников шума (их нет в записанных выше уравнениях), не из-за бесконечного числа степеней свободы (в системе уравнений их 3). Настоящая первопричина нергулярности определяется свойством нелинейных систем экспоненциально быстро разводить первоначально близкие траектории в ограниченной области фазового пространства.

Как измерить хаос? Ответ тривиален − по показателям Ляпунова. Хаос в детерминированных системах подразумевает чувствительную зависимость от начальных условий. Это означает, что две траектории, близкие друг к другу в фазовом пространстве в некоторый начальный момент времени, экспоненциально расходятся за малое в среднем время [31].

Такие системы в нелинейной динамике называются системами с перемешиванием, если с течением времени (tr) информация о начальных условиях в них полностью утрачивается. О перемешивании мы судим по показателю Ляпунова, точнее по наибольшему из них.

Как вычисляются показатели Ляпунова в наиболее простых задачах нелинейной динамики? Если в системе δη0 − мера начального расстояния между двумя исходными точками для параметра порядка (переменной) η, то, спустя малое время, расстояние между траекториями η(t)/ и η(t)//, выходящими из этих точек, становится равным

86

Термодинамика открытых систем

δη( t ) = δη0 exp(λt ),

(5.9)

где λ − показатель Ляпунова (рис.5.3).

	δη(t)	0.1
	t)0.011		η(t)
	0.01
	1 .10	3
	1 .10	4
	δn ,1	5	λ<0
	1 .10
	1 .10	6

а1 .10 7

					10− 8 .									8
						1			10		0						200					400							600					800									t 1000
											0														t(n) , s																		1000
											10											η(t)
				2.978
											1
				δη(t)							0.1
												0.01
						1		.	10						3
				δ	n ,1	1		.	10						4
						1		.	10						5
				D( s) 1				.	10						6
						1		.	10		7
						1		.	10						8
																							tr
						1		.	10						9
				б	1	..	10				10
											11
		7.788 ×10			− 121		10				12
					1	.	10
											0						500					1000							1500												2000
											0														t(n) , s																		t
																																									2200

Рис.5.3. Хаос и эволюция “расстояния” между двумя расчетными траекториями уравнения (5.7) при заданных отличающихся начальных условиях. Расстояние между двумя соседними

траекториями η(t)/					и η(t)//	определялось	величиной
δη(t)=		η(t)/ − η(t)//		;	a) δη0=8 10−3,	λ=−0.018<0;	б) δη0=10−9,

λ=0.018>0. tr – характерное время, за которое система забывает начальные условия.

87

Термодинамика открытых систем

При этом расстояние между двумя расчетными соседними траекториями определяется величиной δη(t)= η/ − η// .

На рис. 5.3а представлены регулярные колебания δη(t) (показатель Ляпунова λ<0), на рис. 5.3б − хаотические пульсации (λ>0). Детерминированный хаос имеет место вблизи двух аттракторов. В этом случае время жизни детерминированной траектории (tr) является ограниченным.

2.5

2

Zηn+1

n + 2 , 1

1

а

0.5

0.5	1	1.5	2	2.5
0.5		Zηn ,n1		2.5

2.5

2

Z n + 30 , 1

ηn+30 1

б	0.5
			1		1.5		2		2.5
	0.5
	0.5				Zηnn, 1				2.5

Рис.5.4. Псевдофазовые портреты решений уравнения

(5.7) для ∆=1 (а) и ∆=30 (б).

Для системы можно указать область параметров, в ко-

88

Термодинамика открытых систем

торой решения ведут себя хаотически, это − область детерминированного хаоса λ>0. При λ>0 соответствующий режим является локально неустойчивым и хаотическим; при λ=0 – нейтрально устойчивым; при λ<0 режим является устойчивым и периодическим. Для хаотических состояний решения ДУ (5.7) являются необратимыми, т.к. за время tr система полностью забывает начальные условия.

В углах рисунков находятся расчетные значения траекторий η(t)/.

О необратимости описываемых физических процессов говорят и псевдофазовые портреты ηn+∆ = f (ηn ) , представлен-

ные на рис.5.4. На них приводятся зависимости каждого последующего значения от предыдущего; с каждым шагом расчета n зависимость становится более размытой, хотя по-прежнему детерминированной и детерминированной достаточно сложным образом.

Таким образом, поведение термодинамической хаотической системы во времени оказывается сложным. Система объединяет в себе локальную неустойчивость – малые погрешности начальных данных нарастают и близкие траектории расходятся, и глобальную устойчивость, когда траектория не уходит из некоторой области фазового пространства.

5.5. Энтропия Колмогорова

Энтропия Колмогорова (Колмогоров, 1954) – важнейшая характеристика хаотического движения в фазовом пространстве произвольной размерности.

Вспомним, что термодинамическая энтропия S есть мера беспорядка в данной системе. Простой пример системы, в которой S растет, − молекулы газа, которые вначале помещены в одну половину куба и которым затем внезапно открывается возможность заполнить весь сосуд. Беспорядок в системе нарастает, так как молекулы больше не отделены от другой половины куба. Этот беспорядок связан с ростом нашего незнания о состоянии системы (до того как была убрана перегородка, о расположении

89

Термодинамика открытых систем

молекул мы знали больше).

Более строго, энтропия S, определенная как

S ≈ −∑Pi ln Pi ,

i

где {Pi} − вероятности для системы оказаться в состояниях {i},

есть мера информации, необходимая для определения местоположения системы в некотором состоянии i, т. е. S есть мера незнания о системе (Shanonn, 1949). Если при определениии S(t) перейти от натурального логарифма к десятичному, то S будет измеряться в бит.

Этот пример из статистичесчкой механики показывает, что по существу беспорядок есть понятие из теории информации. Г.Шустер [27] отмечает, что энтропию Колмогорова K0, показывающую “насколько динамическая система хаотична”, также можно определить формулой Шенона, так что K0 пропорциональна скорости потери информации о состоянии динамической системы с течением времени. Для одномерных отображений K0 является также и показателем Ляпунова. Итак, энтропия Колмогорова (метрическая энтропия) пропорциональна скорости потери информации о состоянии системы с течением времени и является мерой экспоненциальной скорости разбегания траекторий динамической системы. Определение метрической энтропии является необходимым элементом комплексного анализа на детерминированный хаос, она может быть использована в анализе фазовых переходов в различных системах.

Время, за которое система забывает начальные усло-

вия. При определении информационной энтропии в виде S(t)=K0t (t→∞) со сколь угодно большой точностью огрубления фазового пространства µ→0 энтропия максимума не достигает. Анализ существенно упрощается, если зафиксировать конечный порядок огрубления фазового пространства µ0, тогда за время tr область

∆Γ=µ0 расширяется до предельного значения ∆ Γ_ = δη , послед-

нее связано с размером описываемого аттрактора. В результате время жизни фазовой траектории связано с метрической энтропией К0 = λ точной формулой:

90

Термодинамика открытых систем

	1	ln			;
tr =				δη		(5.10)
			µ0
	K0

отметим что в формуле Г.М. Заславского предельное значение нормировано: δη = 1 [32]. На рис.5.3б расстояние между двумя

траекториями меньше этого значения.

Другими словами, точное предсказание состояний нелинейной системы возможно только на интервале времени tr, а на временах, больших tr, возможны лишь статистические предсказания. Для одномерного отображения энтропия Колмогорова равна положительным значениям показателя Ляпунова: K0=λ>0 [27].

Вычислив, таким образом K0, можно определить время разбегания двух соседних траекторий за время tr≡tr/t0. При полной неустойчивости различие в траекториях растет со временем экспоненциально. Для конкретно заданной термодинамической системы с фазовыми переходами, таким образом, можно определить будет ли ее движение неустойчивым.

Небольшой сбой с таких траекторий приводит к практически непредсказуемому поведению фазовой траектории и анализ таких явлений является чрезвычайно важным, как мы видели выше, для понимания необратимости, так как начальные условия для физических систем задаются всегда с ограниченной точностью. Именно это и обуславливает невозможность долгосрочного динамического прогноза состояния динамической системы. Энтропия Колмогорова (на самом деле производство энтропии

K0 = dS / dt >0) может служить своеобразным индикатором пе-

риодического (квазипериодического) поведения параметра порядка (K0=0), хаотического (K0>0) и случайного (K0→∞). Для регулярного движения первоначально близкие точки остаются близкими. Для хаотического движения первоначально близкие точки расходятся экспоненциально. Для случайного движения первоначально близкие точки распределяются с равной вероятностью по всем возможным интервалам.

91

Термодинамика открытых систем

5.6.Переход от непрерывных термодинамических уравнений к дискретным (отображениям)

Дискретный характер протекающих процессов возникает при решении некоторых частных задач фазовых переходов в межфазном слое в системе жидкость−пар, при химических реакциях [30,33] и др., т.е. там, где можно выделить прямой процесс и обратный ему. Системе дифференциальных уравнений, но более высокого порядка (содержащую большее число переменных) можно сопоставить отображение – уравнение в дискретной форме для одной или двух переменных.

Метод дискретных отображений в последнее время широко используется при моделировании нелинейных систем. Первое отличие его от непрерывных моделей, в том числе и для теплофизических систем, состоит в том, что отслеживаются значения динамических переменных ηk (k=1,2,3,….m, m − номер временного шага) в определенные моменты времени, при этом ин-

тервалы времени ∆t = tk +1 −tk не малы и что происходит с пере-

менными в промежуточные моменты времени не исследуется. Второе отличие связано с тем, что вместо дифференциальных уравнений используются рекурентные соотношения (отображения), связывающие значения переменных со значением их в момент времени tk . Например, при химических реакциях, так и при процессах испарения и конденсации в пространственно протяженном межфазном слое реализуются промежуточные стадии, когда за время ∆t процесс повторяется. В системе жидкость−пар

при испарении ηk = ρ*kL − ρ*0 >0 – отклонение плотности жидкости ρ*kL от среднего значения ρ*0 в центре межфазного слоя в k−й

момент, ηk+1 − в следующий момент. При этом промежуточный режим конденсации при феноменологическом описании в дискретной модели не фигурирует, однако в ДУ он должен учиты-

o

ваться, например различные знаки у η и η в уравнении (5.7)

описывают или процессы испарения, или процессы конденсации. Может быть предложен следующий алгоритм перехода к

92

Термодинамика открытых систем

уравнениям, дающим при сохранении классических свойств фазовых переходов, их новые характеристики. Эти характеристики связаны с появлением в системе детерминированного хаоса, который также можно рассматривать как основу построения моделей флуктуаций в термодинамических системах. Процесc вступления в химическую реакцию, связанный с конечной скоростью диффузии, испарение молекул с малой поверхности и др. рассматриваются как мгновенные «удары», приводящие в такой нелинейной системе к резкому изменению параметра порядка η (плотности, концентрации и др.). При этом реализуются промежуточные стадии, когда процесс повторяется. Следуя [27,33], от модели (5.7) перейдем к каноническому уравнению с δ−функцией Дирака в правой части

oo	o				∞
η+ η = f (η)∑δ(t − kT0 ) ,
					k =0
f (η) = −				∂G* = −(η3		+ a*η+ b* ) .				(5.11)
					∂η
Здесь k=1,2…m, T	= T /	/ t	0		. Динамическое		уравнение			(5.11),
0	0
таким образом, представлено в виде:
t = kT						oo o		*		(5.12)
						η+ η = − ∂G			,
	0						∂η
t ≠ kT0						oo	o
						η+ η = 0 .

Далее рассмотрим класс задач с последействием, для которых переменная η определена для момента времени t, а амплитуда удара f для момента времени (t−τ), т.e. задачи со временем ретардации τ. Раскладывая в ряд Тейлора функцию f(t−τ) по малому параметру τ и ограничиваясь двумя членами разложения, получаем перед производной η по времени

Γ( t ) =1 + τ( df ( η) / dη) =1 − τ( 3η2 + a* ) , η = η( t ) .	Будем пола-
гать что Γ(t) = Γk является кусочно-постоянной	функцией, а

длительность ударов гораздо меньше времени между ними T0/ . 93

Термодинамика открытых систем

Интегрируя полученное уравнение

oo	o	∞
η+ Γ(t) η = f (η)∑δ(t − kT0 )			(5.13)
		k =0
на конечном временном	интервале	(k +1)T0 −ε > t > kT0 −ε ,

где ε→0, переходим, следуя [29, 33], к двумерному отображению, когда сплайн для неравновесного коэффициента затухания имеет вид Γk =1 − τ( 3η2k + a* ) .

η

0

0

100

200

300

t

а

T0=1τ=0.03

λ

a*

b*

б

Рис.5.5. Хаотическая динамика параметра порядка (а) и показатель Ляпунова λ (б) для термодинамической системы, описываемой отображением (5.14). Хаос имеет место при λ>0 (заштрихованные области (б)), T0=1, τ=0.03.

В результате получаем двумерное отображение

94

Термодинамика открытых систем

ηk +1	= ηk −T0	η3k + a ηk +b
				;	(5.14)
		1−τ (3ηk2 + a )
yk +1 = yk −(1−T0 )(η3k			+ a ηk +b ) .		(5.15)

Отношение τ/T0 определяет для отображения (5.14) различную степень неравновесия в рассматриваемой системе.

При уменьшении отношения τ/T0 характеристики итерируемого процесса приближаются к равновесным. Время строби-

рования ∆t может быть выбрано в виде ∆t=T0=1 ( t0 = T0/ ). В ре-

зультате двумерное отображение (5.14), (5.15) становится одномерным и предстает в форме (5.14), что существенно облегчает нелинейный анализ рассматриваемой нелинейной задачи, которая ранее сводилась к системе 3−х нелинейных дифференциальных уравнений.

Отображение (5.14) является по сути дискретным представлением уравнения Халатникова−Ландау, широко распространенного в теории фазовых переходов [18], на которое наложено условие последействия. Здесь оно дополнено также условием запаздывания. Отметим, что известные в нелинейной динамике отображение Хенона и логистическое отображение получены аналогичным образом, их вывод приведен в [27].

Уравнение эволюции в дискретной форме (5.14), дает не только периодические, релаксационные, но и хаотические решения (см. Рис.5.5). Хаотические решения также имеют скорости изменения энтропии, свободной энергии и других термодинамических характеристик. Поскольку связи между ними на термодинамическом уровне выявлены и они представлены в виде уравнений, то все эти термодинамические характеристики также могут быть исследованы на хаос. Это означает, что мы имеем удобный способ моделирования флуктуаций в нелинейных системах, обусловленных не случайными значениями, а детерминированными нелинейными особенностями самой локальнонеравновесной системы.

95

Термодинамика открытых систем

5.7. Бифуркационные диаграммы

Исследование хаоса подразумевает получение бифуркационных диаграмм и соответствующих им показателей Ляпунова [27, 33]. Поэтому вернемся к рассмотрению отображения (5.14) и его свойствам. Бифуркационная диаграмма, построение которой является довольно интересным занятием, показывает зависимость решений уравнения (отображения) от тех или иных управляющих параметров. Диаграмма имеет вид вилки, от которого и произошло слово “бифуркация” (от французского слова bifurkftion – раздвоение, ветвление).

Для описания перехода от циклического поведения переменной к хаотическому при изменении управляющих параметров отображения были использованы бифуркационные диаграммы, которые для переменной ηk могут быть построены от параметров a, T0, τ, b (для катастрофы сборки. Для рассматриваемой катастрофы на рис.5.6а представлена бифуркационная диаграмма и, соответствующие ей значения показателя Ляпунова λ (рис. 5.6б). Значения λ определялись по формуле

λ =	lim	1	N	ln		dϕ(η	k	)		,	ηk +1 = ϕ(ηk ),
			∑
						dηk
	N →∞ N k =1
где N− число итераций отображения,											функция ϕ(ηk )- правая

часть отображения (5.14), которую надо продифференцировать.

Непрерывное изменение управляющих параметров приводит к каскаду бифуркаций, которые проявляются в виде ветвлений на бифуркационной диаграмме и сопровождаются удвоением периода, связанным с субгармонической неустойчивостью. Каждое из ветвлений соответствует потере устойчивости одной из неподвижных точек и образованию двух устойчивых. При этом система распадается на две новые фазы, которые соответствуют двум устойчивым точкам: x+ и x−. Теперь каждая последующая итерация переводит систему из одной фазы в другую. Таким образом, аттрактор с периодом 1 сменяется аттрактором с

96

Термодинамика открытых систем

периодом 2 [27].

Выше критических значений τ∞≈0.266 и а∞≈−1.85 в описываемой системе начинается область так называемого детерминированного хаоса, где параметр порядка ведет себя хаотически. Расчет всех точек бифуркаций ренормгрупповым методом, как это выполнялось для логистического отображения [31], затруднен вследствие сложности полученного отображения. Из рис. 5.6 видно, что в области хаоса имеются участки с периодической динамикой параметра порядка − окна детерминированности (светлые полосы), соответствующие отрицательным показателям Ляпунова.

ηk		η+			τ=0.14 T0=0.35
1		η-			−a
				Ф1=
0
				Ф2=-	−a
1
					a
0.5		a∞	a1
λ 0
-0.5
						б
-1.5	2		1.5	1	0.5	0 a

Рис.5.6. Бифуркационная диаграмма (а) для переменной ηk отображения сборки и его показатель Ляпунова (б) при

T=0.35, τ=0.14.

В отличие от логистического отображения, в котором имеется всего один управляющий параметр, исследуемое ото-

97

Термодинамика открытых систем

бражение (5.14) являются многопараметрическим; для таких систем важно знать характер их поведения в зависимости сразу от нескольких управляющих параметров. Этот вопрос является также интересным с точки зрения управления хаосом − темы популярной в последнее время. При наличии, например, плоской или трехмерной области управляющих параметров границы между областями с различным поведением не сводятся к точкам бифуркации, а представляют собой кривые или поверхности (см.

Рис.5.7).

Это область прогнозируемой динамики. В области хаотического движения (λ>0) имеющиеся пики, уходящие в область отрицательного λ, соответствуют окнам детерминированного поведения. Это тоже область прогнозируемой динамики, при λ>0 время прогнозирования ограничено.

T=1

λ

τ

C

A

B C`

a

Рис. 5.7. Двухпараметрическая зависимость показателя Ляпунова λ(τ, а) для отображения сборки при T0=1; в области хаоса λ(τ, а)>0; A−область хаоса; B−область регулярного движения; CC`− граничная кривая перехода к хаосу.

Наглядное представление о таком поведении, а также о сложной структуре областей хаоса и регулярного движения можно получить при помощи трехмерных диаграмм, отражающих

98

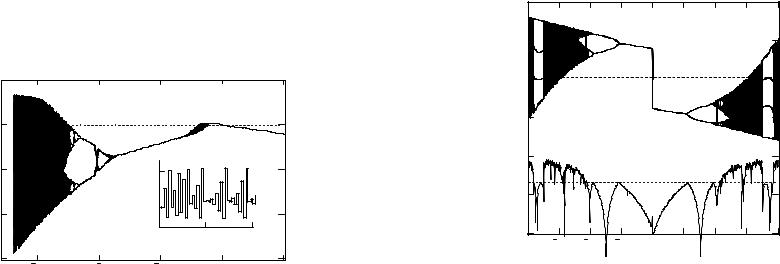
Термодинамика открытых систем

зависимость показателя Ляпунова от двух параметров (рис. 5.7). В плоскости управляющих параметров всех трех диаграмм изображены некоторые контурные графики из линий равного уровня для различных значений λ. Аномальные пики в области регулярного движения (λ<0) соответствуют различным режимам периодического движения, характеризуемых периодом, амплитудой и т.д. Для каждого временного интервала коэффициент затухания является кусочно-постоянной функцией, последнее соответствует пошаговым временным значениям статистических данных.

Γk τ=0.02T0=

1

0.95		1		a=-1.3
		Γk
0.9		0.9
			0	20		t=kh
						t=kT0
0.85	1.5	1	0.5		0	a

Рис.5.8. Бифуркационная диаграмма для коэффициента затухания Гk отображения сборки.

На рис.5.8. приведена бифуркационная диаграмма для нелинейного коэффициента затухания отображения сборки

(5.14): Γk =1 − τ( 3xk2 + a ) . Приведены также пошаговые его зна-

чения, установленные численными методами, что подтверждает выполнимость двух условий, при которых решалась задача: зависимостью коэффициента затухания от времени и ее кусочнопостоянной характер, связанный с его нелинейной зависимостью от ηk. Анализ бифуркационных явлений для отображения (5.14) был бы неполным без анализа влияния управляющего параметра b как на сами бифуркации, так и на показатель Ляпунова. На рис.

99

Термодинамика открытых систем

5.9а приведена бифуркационная диаграмма для переменной ηk отображения сборки (5.14) и его показатель Ляпунова λ при постоянных остальных параметрах.

	2				τ=0.02 a= -0.6 T0=1
	ηk
	1
	0
		a
	1
	0.7				б
	λ
	-0.3
	-1.3							b
	0.6	0.4	0.2	0	0.2	0.4	0.6

Рис. 5.9. Бифуркационная диаграмма (а) для переменной ηk(b) отображения сборки и его показатель (б) Ляпунова λ(b) при

T0=1, τ=0.02; a=−0.6.

Как на бифуркационной диаграмме, так и нижней кривой зафиксированы широкие окна детерминированного поведения. Показатель Ляпунова для решений в окнах меньше нуля. Эти полосы иллюстрируют фрактальную природу описываемых процессов, т.к. в каждом из окон бифуркационная диаграмма повторяется, хотя и в более уменьшенном виде. В точках бифуркаций показатель Ляпунова принимает нулевые значения.

5.8. Хаос и необратимость

Получаемые в рамках нелинейной динамики результаты не противоречат классической теории неравновесных процессов

100

Термодинамика открытых систем

(термодинамике необратимых процессов), дополняя последнюю новыми возможностями, в том числе возможностью описания флуктуаций в виде хаотических пульсаций, которые она не могла учитывать, алгоритмами описания устойчивости по Ляпунову равновесных и стационарных состояний и описать возникновение необратимости по времени. Для таких хаотических термодинамических систем могут быть построены бифуркационные диаграммы, рассчитаны показатели Ляпунова, определено время необратимости Колмогорова.

Что очень важно, то это то что для хаотических состояний термодинамических систем может быть также как и в нелинейных задачах механики определена энтропия Колмогорова, характеризующая скорость забывания системой (локальным объемом) начальных условий. Такой подход устанавливает связь между необратимостью по времени неравновесных термодинамических процессов и энтропией Колмогорова K0:

S(t)=K0t, K0 = dSdt ≥ 0 .

Являясь по существу производством энтропии, K0 ха-

рактеризует меру экспоненциальной скорости разбегания траекторий термодинамической системы. Описываемые необратимые термодинамические процессы определяются временем необратимости tr.

Отметим в заключении, что алгоритмы вычисления энтропии Колмогорова для конкретных задач теплофизики приводятся в статьях [28,29, 33]. Оказывается, что такому анализу поддаются процессы в межфазном слое, в котором имеют место прямой и обратный ему нелинейные процессы – испарение и конденсация [28,29], прямая и обратная реакции для химических реакций [33]; отметим также процессы плавления и кристаллизации [30]. Особенно привлекательным выглядит применение этих идей в сейсмологии.

При этом полученное уравнение (5.7) описывает фазовые переходы I и II рода с хаотической динамикой параметра порядка, в том числе гомофазные и гетерофазные флуктуации параметра порядка, давления, температуры, а также конечное время

101

Термодинамика открытых систем

жизни фазовой траектории, метастабильные состояния, гистерезис. Подход позволяет соотнести такие понятия как взрывной фазовый переход в двухкомпонентных термодинамических системах, хаос и нелинейные процессы, а также ответить на вопрос − реализуется ли в нелинейных термодинамических системах детерминированный хаос и как быстро теряется в них информация о начальных условиях. Рассмотрение же процессов в более общем виде, которое выполнено в данном пособии, когда переменными являются термодинамические силы или потоки, является чрезвычайно важной задачей для теплофизики. При этом причинами нерегулярности и непредсказуемости является собственная нелинейная динамика термодинамической системы, а не влияние шумов и внешних возмущений.

5.9. Примеры термодинамических хаотических систем

Межфазный слой в системе жидкость-пар. Рассмотрим тонкий слой жидкости и пара малого, но конечного объёма, включающий границу раздела фаз. Изменение плотности единичной толщины такого слоя ρх=ρ во времени под действием давления P, температуры T, которые считаются одинаковыми для всего межфазного слоя, может быть представлено в виде однороднего нелинейного уравнения с полиномом третьей степени в правой части [29]:

dρ

= −

k

ρ +

k

ρ2 −

k

ρ3

+

k

P

,

dt

1

2

3

4

T

где ki некоторые параметры задачи (i=1,…,4), определяющие в

общем случае непрерывное изменение плотности межфазного слоя по толщине. Первоначально будем считать эти параметры постоянными. Здесь используется полином третьей степени, так как в качестве равновесных решений уравнения имеет место три значения, что вполне достаточно для описания двух устойчивых состояний (жидкость и пар) и одного неустойчивого. Задача решается при следующих граничных условиях для межфазного слоя: x=0 ρ0=ρL; x=∆=2 l ρ∆=ρG..

102

Термодинамика открытых систем

В приводимой модели ρx - в общем случае сложная нелинейная функция расстояния х. В линеаризованном представлении эту функцию можно принять линейной функцией расстояния x. Отметим, что при ρx=ρ0, что имеет место в середине межфазного слоя (x= l ), задача существенно упрощается. Параметр порядка

η= ρ* − ρ*0 в этом случае характеризует в феноменологической модели отклонение приведенной плотности ρ* от среднего зна-

чения приведенной плотностиρ*0 . Такой подход приводит к ото-

бражению (5.14), которое при определенных условиях дает хаотические решения (см. рис.5.10).

В динамике как объема, так и давления также выделяются турбулентные (область частых пульсаций) и ламинарные (область медленных пульсаций) временные фазы описываемого нелинейного процесса.

3

2

			1
0	50	100	150	t

Рис.5.10. “Гигантские”флуктуации в межфазном слое. Результат компьютерного моделирования возникновения флуктуаций давления большой длительности вблизи критической точки. (кривая 1, T*=0.9942994), эта кривая сравнивается качест-

венно с кривой 2 (T*=0.9346414) и кривой 3 (T*=0.7291529); T0=1 [29].

Такой анализ становится возможным вплоть до критической точки фазового перехода второго рода, которая определяет предельное двухфазное состояние как трижды вырожденную критическую точку (η=a*=b*=0). При приближении к критической точке (T*→1) длительность ламинарных фаз возрастает. Численные расчеты показали, что в очень малой окрестности

103

Термодинамика открытых систем

критической точки время жизни ламинарных фаз на порядки больше (рис.5.10, кривая 1), чем вдали от нее (рис.5.10, кривые 2,3), что соответствует гигантским (по времени) флуктуациям, наблюдаемым в экспериментах. Это явление вблизи критической точки получило название критического замедления.

Хаотическая проводимость ионных каналов. Сегодня ос-

новными поставщиками новых концепций и базовых моделей наряду с физикой, химией становятся биология, нейронаука, экономика и др. Следует обратить особое внимание на биологию и ее некоторые задачи, в частности задачи о проводимости ионных каналов, сокращении саркомеров и т.д. Для этого можно использовать при описании электрической проводимости ионных каналов для параметра порядка (отклонение канального тока от равновесного значения) нелинейное ДУ второго порядка (5.7) с запаздыванием и релаксацией при периодическом воздействии на ток в канале [40].

Параметр порядка η связан при таком подходе с отклонением канального тока (термодинамического потока) Ji=i от среднего значения i0 в приведенном виде

	η=	i	−	i0	,
		ic		ic

здесь xс=iс – некоторый масштаб потока.

Численные расчеты модельного уравнения (5.7) показывают при наличии релаксации и последействия на хаотическую динамику параметра порядка и конформационного потенциала канального белка с положительными коэффициентами Ляпунова.

Путем масштабирования времени расчетные данные для параметра порядка можно привести к соответствующим эксперименту временным интервалам. При этом время масштабирования t0 2.5 10−4с соответствует времени конформационных переходов канального белка. В целом данная модель при выбранном значении t0 удовлетворительно описывает экспериментально наблюдаемую динамику тока (рис. 5.11б). При этом могут быть построены бифуркационные диаграммы, показывающие зависимость проводимости от управляющих параметров, определены спектры пульсаций тока, показатели Ляпунова и другие характе-

104