Mueller M.R. - Fundamentals of Quantum Chemistry[c] Molecular Spectroscopy and Modern Electronic Structure Computations (Kluwer, 2001)

86

Chapter 5

The Schroedinger equation for this system can now be readily written.

The solution to this differential equation is well known. The energy eigenvalues are quantized as follows:

and

The wavefunctions can be expressed in the following manner:

The functions in Equation 5-5 are polynomials Hermite polynomials. The Hermite polynomials can be following formula:

in z known as the generated from the

Particles Encountering a Finite Potential Energy

87

The Hermite polynomials for the state (the next state) can also be obtained from the following recursion relationship given that

The first six Hermite polynomials are shown in Table 5-1.

The normalization constant for the wavefunction is obtained by integrating the wavefunction squared (the wavefunction is real for the harmonic oscillator) over all space. As mentioned previously, only an infinite potential can completely contain a particle in a limited region of space. Since the potential for the system approaches infinity at the limit that x approaches infinity, the limits on the integration overall space must be

88

Chapter 5

Example 5-1

Problem: Demonstrate that the ground-state harmonic oscillator wavefunction is (a) normalized and (b) is orthogonal with the first excited state.

Solution:

(a) The ground-state wavefunction, 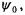is written as follows:

If the wavefunction is normalized, the following integral must be equal to one.

This confirms that the ground-state wavefunction is normalized. Based on this result, it is extrapolated that the rest of the wavefunctions are all normalized though the normalization constant is different for each level of

(b) The wavefunction, 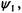can be written as follows:

If the wavefunctions are orthogonal, then the following integral is equal to zero.

This demonstrates that the wavefunctions and are orthogonal. This is true for all of the harmonic oscillator wavefunctions.

Particles Encountering a Finite Potential Energy

89

Example 5-2

Problem: Determine explicitly the energy eigenvalue for the ground-state of the harmonic oscillator by using the Schroedinger equation.

Solution:

This is the same result as obtained from Equation 5-3:

The first several wavefunctions for the harmonic oscillator are shown in Figure 5-1 and should be compared to the Particle-in-a-Box wavefunctions shown in Figure 2-2. Note that the wavefunctions for the Particle-in-a-Box and the harmonic oscillator have similar shapes for each corresponding energy level. The principal difference is that the harmonic oscillator wavefunctions asymptotically approach zero as x approaches infinity (as the potential approaches infinity). Because the wavefunctions must

90

Chapter 5

asymptotically approach zero as x approaches infinity, this results in curvature in the wavefunctions and consequently the ground-state energy is non-zero.

To better understand the quantum mechanical harmonic oscillator, the results of the quantum mechanical system can be compared to those for the classical mechanical system (described in Section 1.3). The classical turning point for the mass, occurs when the energy of a given state is equal to the maximum potential energy of the system. This is done using the ground-state quantum mechanical energy.

Solving for the classical turning points,

Particles Encountering a Finite Potential Energy

91

In the classical mechanical harmonic oscillator, the points correspond to where the probability of finding the particle is the greatest since the mass stops at these points (zero kinetic energy), and the probability of finding the particle beyond these points is zero.

This “leaking out” of the wavefunction as it asymptotically approaches zero can be seen quantitatively by computing the probability density of the

particle beyond the classical turning points	This is done specifically
for the ground-state in the regions of	and	where

classically it would be predicted that there should be zero probability of the particle existing because the potential energy exceeds the energy of the particle.

Probability of the Particle Beyond the classical turning points for

The integral in Equation 5-12 cannot be solved analytically; however, it can be solved numerically by setting the constant c to any value (the result is independent of the value of the constant c). As can be seen by the results in Table 5-2, the probability of the particle to exceed the classical turning points decreases as the value of increases. This is in part because the region of space that the particle is being confined to by the potential is getting larger (note that is increasing with ), and the curvature of the function is increasing due to the increased kinetic energy of the particle.

The points of maximum and minimum amplitude for the harmonic oscillator wavefunctions (indicative of the greatest probability of the mass) can be found by taking the first derivative of the wavefunction and setting it equal to zero.

92

Chapter 5

The result for the ground-state is analogous to the classical system. The greatest probability of finding the particle is at the equilibrium position for the spring. However, the ground-state energy is not zero, as in the classical mechanical harmonic oscillator. The classical analogy is that the particle is not at rest even in the ground-state. The points of greatest probability densities are done for several other states, and the results are listed in Table 5-3. As the value of increases, so does the curvature resulting in an increasing number of nodes just like in the Particle-in-a-Box wavefunctions.

Another interesting feature of the quantum mechanical harmonic oscillator is that the energy difference between subsequent levels is the same: This feature of uniform energy levels is a result of the symmetry of the system.

Particles Encountering a Finite Potential Energy

93

94

Chapter 5

The system can now be expanded for describing a diatomic molecule. In this case, the spring is separated by two different masses as shown in Figure 1-2. The Schroedinger equation can be written as follows:

Separation of variables can be obtained by using the center-of-mass coordinate system as described in Section 1.3. Recall that the center-of- mass coordinate system introduces the following coordinates:

The coordinate r represents the displacement of the spring from its equilibrium position, and the coordinate s corresponds to the center of mass of the system. Using this coordinate system results in the following Schroedinger equation that is similar in form to the expression in Equation

1-18.

The term is the reduced mass, and M is the total mass of the system.

As discussed previously in Section 1.3, the kinetic energy operator,

Particles Encountering a Finite Potential Energy

95

corresponds to the translation of the entire system in space. Since only vibrational motion is of interest and the coordinates s and r are separable, the Schroedinger equation is reduced to the coordinate r.

Equation 5-14 is mathematically equivalent to Equation 5-2. As a result, Equation 5-14 produces the same results as before with the reduced mass instead of m and the coordinate r instead of x. The following expressions are changed, and the rest of the expressions from before remain the same.