Варламов Линейные електрические цепи переменного тока Част ИИ 2008

Покажем, что при резонансе напряжений максимумы энергии

LI 2

магнитного поля в индуктивном

W

Lmax

=

m

и электрического

2

CU 2

поля в емкости

WC

=

Cm

равны.

max

2

В самом деле, рассмотрим разность:

W

= W

− W

=

LI m2

−

CU С2m

=

1

ω

LI 2

− ω

CU 2 .

LCmax

Lmax

Cmax

2

2

2ω0

0

m

0

Cm

Вынесем за скобки ω0C и учтем, что при резонансе напряже-

ний ω0 L =

1

, тогда:

ω0C

C

WLCmax

=

(ω0 LI m2 )2

− U Cm2 .

(2.6)

2

В рассматриваемом режиме, как было показано выше, между величинами U L и U C существует соотношение: U L = −U C . Так

как U Lmax =|U L | , а U Cm =|U C | , то из этого следует, что в резонансе напряжений U Lm = U Cm . Принимая это во внимание, а также, что U Lm = ω0 LI m , можно заключить, что

WLCmax = 0 ,

что и доказывает искомое утверждение.

На рис. 15 изображены зависимости величин WL и WС от вре-

мени t.

Как следует из рис. 15 при резонансе напряжений происходит непрерывное перераспределение энергии (энергообмен) магнитного поля в индуктивности и энергии электрического поля в емкости. При этом суммарная энергия:

W

= W

+ W

=

LI m2

cos2

ω

t + sin 2

ω

t

=

LI m2

=

CU Cm2

.

LC

L

C

2

0

0

2

2

21

Рис. 15

Таким образом, в режиме резонанса напряжений периодически происходит равный энергообмен между индуктивным и емкостным элементом, когда энергия, первоначально накопленная в контуре, «колеблется» между L и C , без участия в этом процессе источника. При этом вся электрическая энергия, поступающая в цепь в режиме резонанса напряжений, расходуется в сопротивлении. Для контура без потерь (r = 0) в режиме резонанса в цепь не поступала бы энергия от источника.

2.1.3. Частотные характеристики последовательного колебательного контура

Комплексное	сопротивление				последовательного контура
(см. рис.12) можно представить в следующем виде:
		1				ω			1
Z = r + j	ωL −		= r + jω0L					−			=
						ω0			ωω0 LC
		ωC									(2.7)
			ω		ω0
	= r + jω0 L				−	ω .
				ω0
			22

С другой стороны, E = Z I , а Z =| Z | e jϕ , где φ – фазовый

сдвиг приложенного напряжения относительно тока. В соответст-

вии с (2.7):

	ω	L ω			ω	0
ϕ = arg tg	0			−			.	(2.8)
	r	ω0			ω

Последнее выражение называется фазочастотной или фазовой характеристикой (ФЧХ) последовательного колебательного контура.

Эта же зависимость представлена в виде графика φ(ω) на рис. 16.

Рис. 16

Зависимость φ (ω) обращается в ноль при ω = ω0, что соответствует режиму цепи (резонанс напряжений), который иллюстрирует рис. 14. Для ω < ω0 величина φ становится отрицательной, что соответствует емкостному характеру цепи, а для ω > ω0 величина φ является положительной, что соответствует индуктивному характеру цепи.

Зависимость амплитуд тока и напряжений на емкостном и индуктивном элементах цепи называют амплитудно-частотными характеристиками (АЧХ) последовательного колебательного контура.

Выражения для этих значений можно представить в следующем виде:

23

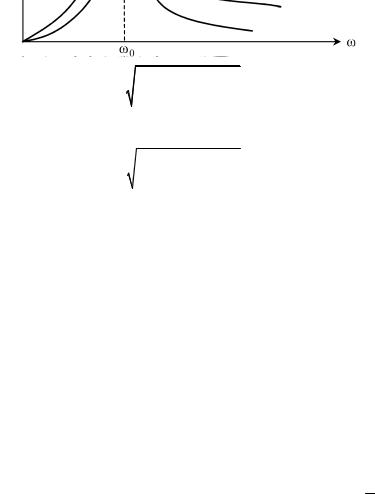
I =

E

;

r

2

ωL −

1

2

+

ωC

U L =

EωL

;

r

2

+

ωL −

1

2

1

ωC

E

U C =

ωC

.

r

2

+

ωL −

1

2

ωC

На рис. 17 представлены зависимости этих величин от частоты.

Рис. 17

Как и следовало ожидать, ток достигает максимума, равного Er ,

в режиме резонанса напряжений (ω = ω0 ) . В этом же режиме U L = U C . При ω стремящейся к нулю и ω стремящейся к бесконеч-

ности, ток стремится к нулю. Это связано с тем обстоятельством, что в первом случае неограниченно возрастает емкостное, а во втором случае индуктивное сопротивление контура.

24

Из выражения (2.1) следует, что настройка контура в резонанс может достигаться за счет изменения частоты генератора, индуктивности или емкости элементов цепи. Первый вариант рассмотрен выше и иллюстрируется рис. 16, 17.

На рис. 18 изображены зависимости тока в последовательном колебательном контуре от индуктивности и емкости цепи.

		Рис. 18
При значении	L = Lрез =	1	цепь переходит в режим резонан-
		ω02C
са напряжений. Такая же ситуация происходит при С = Срез =				1	.
				ω02 L

2.1.4. Добротность последовательного колебательного контура

По определению добротность колебательного контура – это величина, которая определяется следующим выражением:

Q = ω0	Wmax	.	(2.9)
	P
25

где Wmax – максимальная энергия, запасенная в контуре на резо-

нансной частоте, P – мощность активных потерь при тех же условиях.

На резонансе напряжений

LI

2

CU

2

I 2r

W

max

= W

Lmax

= W

Cmax

=

0

=

Cm

. В то же время P =

0

.

2

2

2

Таким образом, выражение для добротности контура приобретает следующий вид:

ω0 L

1

L

ρ

Q =

=

=

C

=

,

(2.10)

r

ω0Cr

r

r

где величина ρ =

L

получила название характеристического со-

C

противления контура.

Из выражения (2.10) следует, что добротность характеризует

степень превышения реактивных сопротивлений ω0 L и

активным сопротивлением r.

Учитывая, что при резонансе U L0 = −U C0 = jω0 LI 0 , а

соответствии с (2.10), получим:

U L0 = −U C0 = Er jω0 L = jEQ .

Из (2.11) следует, что

Q = U L0 = U C0 . E E

1над

ω0C

	I 0	=	E	в
			r

(2.11)

(2.12)

Таким образом, добротность рассматриваемого контура определяется отношением напряжения на L или С при резонансе к величине приложенного к контуру напряжения.

На рис. 19 изображены зависимости амплитуды тока от частоты для двух последовательных колебательных контуров с одинаковой резонансной частотой и разными значениями добротности, причем Q1 > Q2 . Таким образом, как это следует из рис. 19, добротность

26

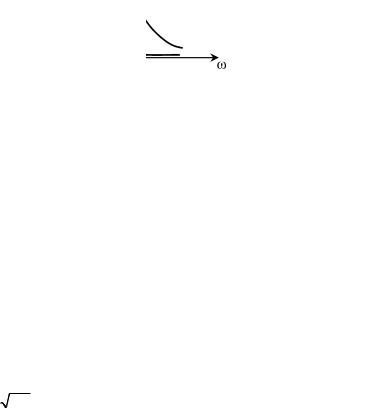
может характеризовать также степень «остроты» резонансной кривой тока вблизи резонансной частоты в последовательном колебательном контуре.

								Рис. 19
							Примеры
Задача 2.1
В		схеме				электрической цепи		рис. 12 r = 10 [Ом],	L = 1 [Гн],
С = 1 [мкФ].						Определить	резонансную частоту ω0 , добротность
контура Q, а также амплитуду синусоидального напряжения на ем-
кости UC, если на вход цепи подано синусоидальное напряжение с
амплитудой 10 мВ на резонансной частоте.
Решение:
В			соответствии с				(2.3)	резонансная частота	контура
ω0 =			1		= 103 рад/с. В соответствии с (2.10) добротность контура
			LC
Q =	ω0 L			= 100 . В соответствии с (2.12) амплитуда напряжения на
		r

емкости U C = Q E = 1 В.

Задача 2.2

Цепь, схема которой изображена на рис. 20, находится в режиме резонанса напряжений. Значение резонансной частоты f0 = 50 Гц. Значение соответствующих амплитуд напряжений и тока в контуре: U = 220 В, U rL = 204 В, U C = 180 В, I = 4 А. Определить параметры индуктивной катушки – r, L, емкость С и сопротивление r1 .

27

Решение:

Рис. 20

U C = U L и ω0 LI = U L ,

1.

На

резонансе

напряжений

отсюда

L =

U C

= 0,143 Гн .

2πf0 I

2.

Напряжение

на

емкости

U C = I

1

,

отсюда

ω0C

C =

I

= 70,8

мкФ.

2π f U

C

0

3.

Комплексная

амплитуда

напряжения

на

катушке

U rL

2

2

1/ 2

U rL = I (r + jω0L) . Отсюда r =

− (2πf0 L)

= 24 Ом.

I

4. В резонансе напряжений (в соответствии с рис. 2 и 3)

U= I (r1 + r) отсюда r1 = UI − r = 31 Ом.

Задача 2.3

При частоте f = 50 Гц сопротивление катушки равно 41 Ом, а

при постоянном токе – 9 Ом. При какой частоте наступает резонанс, если последовательно с катушкой включен конденсатор емкостью C = 51 мкФ?

28

Рис. 21

Решение:

Комплексное сопротивление катушки (последовательное соединение r и L) равно:

				Z = r + jωL .
	При частоте f = 50 Гц сопротивление катушки равно 41 Ом, т.е.
|Z| = 41 Ом,			следовательно	41 = r 2 + (ωL)2 ,	откуда			L =
=	1	| Z |2	−r 2 = 0,127 Гн.	Резонансная частота	f0 =		1		=
	2πf					2π	LC
= 62,5 Гц.

Задача 2.4

Последовательный колебательный контур подключен к синусоидальной ЭДС с амплитудой E = 1,6 В и внутренним сопротивлением R = 16 Ом. При какой величине сопротивления контура r в нем выделится максимальная активная мощность при резонансе напряжений и чему она будет равна?

Решение:

В режиме резонанса напряжений контур эквивалентен активному сопротивлению r. Поэтому в данном режиме цепь будет содержать источник ЭДС с внутренним сопротивлением и активное сопротивление контура (рис. 21).

Всоответствии с теоремой о максимальной активной мощности

внагрузке, в нагрузке выделится максимальная активная мощ-

ность, если Zг = Zн* , где Zг и Zн комплексные сопротивления генератора и нагрузки соответственно. Так как в данном случае Zг = R , а Zн = r , то при r = R = 16 Ом в активном сопротивлении

контура при резонансе будет выделяться максимальная активная мощность:

29

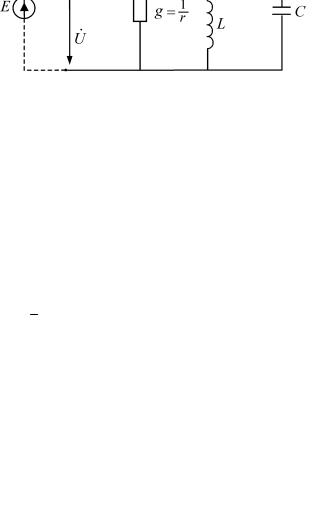
						2	Eд			2
						P = I g	r =			r ,
							R + r
	где	I д		и Eд – действующие значения переменного тока и ЭДС:
	I g	=	I	х, Eg =	E	х . Отсюда P = 20 мВт.
			2		2

2.2.Резонанс токов

2.2.1.Условия резонанса тока

Это явление может возникать в электрической цепи, которая содержит параллельные ветви, причем в одной из ветвей имеется индуктивная катушка (или индуктивный элемент), а в другой конденсатор (или емкостной элемент). Резонанс токов достигается при выполнении условия:

ImY = 0 ,

(2.13)

где Y – комплексная проводимость участка цепи (содержащего указанные параллельные ветви).

Рассмотрим простейшую модель участка электрической цепи (рис. 22) с тремя параллельными ветвями. В одной ветви резистивный элемент с сопротивлением r (и соответственно с проводимо-

стью g = 1r ). Во второй ветви имеется индуктивный элемент, ин-

дуктивность которого L, а в третьей ветви – емкостной элемент, емкость которого C.

Рис. 22

30