Задорожный Методы ядерно-физического мониторинга 2008

Таким образом:

SППП ( E ) =		A0Y ( E )εΦ ( E )		e−μ( E ) r	(1−e−λtbpv )	(6.3а)
		4πr 2λ
SППП ( E ) =	A0Y ( E )εΦ ( E)		e−μ( E ) r tизм ,		при λtизм <<1,	(6.3б)
		4πr 2

где tизм – живое время измерений.

Из (6.3а) и (6.3б) получаем выражение для активности на момент начала измерений:

	A0 =			4πr 2λeμ( E ) r				SППП (E )			(6.4а)
				Y ( E )εΦ ( E )(1−e−λtизм )
A =			4πr 2eμ( E ) r		S	ППП	( E ), при λt		изм	<<1.	(6.4б)
0		Y	( E )εΦ ( E )tизм

На практике для фиксированных геометрий эффективностью ε(E) в пике полного поглощения называют также вероятность того, что гамма-кванта с энергией Е, испущенный источником даст отсчет в соответствующем пике полного поглощения. Очевидно, что тогда выражения для активности принимают вид:

		A0 =			λ	SППП ( E )	(6.5а)
				Y ( E )ε(E )(1−e−λtизм )
	A0	=		1	SППП (E ), при λtизм <<1 .		(6.5б)
			Y ( E )ε( E )tизм

Рассматривая выражения (6.4а–6.5б) очевидно, что алгоритм определения активности следующий:

1)в измеренном спектре выделяют пик полного поглощения;

2)определяют положение пика на шкале амплитуд (номеров каналов), для этого, например можно считать, что положение пика

CППП определяется центроидой пика:

CППП = ∑i Ni / ∑Ni ,		(6)
ППП	ППП

где i – номер канал, Ni – отсчет в канале, и суммирование проводится по области пика.

101

3) по энергетической калибровке оценивают соответствующую положению энергию E(CППП) и, если это возможно, по таблицам ядерных констант определяют, какому гамма-излучателю эта энергия соответствует и уточняют соответствующее значение энергии Е; если однозначный вывод сделать невозможно, повторяют пп. 1–2 до тех пор, пока гамма-излучатель не идентифицирован;

4)для найденного гамма-излучателя по таблицам определяют постоянную распада λ и квантовый выход Y(E) для данной энергии

Е;

5)по имеющейся для данного спектрометра калибровке по эф-

фективности определяют значение εΦ(E) или ε(E) и делают оценку эффективности по формулам (6.4а,б) или (6.5а,б).

6)повторяют процедуру для остальных пиков полного поглоще-

ния.

В результате проделанной процедуры может оказаться, что для какого-либо гамма-излучателя оценка активности проведена для нескольких пиков полного поглощения. В этом случае эту информацию можно использовать для получения более точной оценки, что будет обсуждаться несколько позже. В любом случае получение оценки подразумевает, что мы должны оценить саму величину

иее погрешность.

2.Учет погрешностей при обработке спектров

Результат любого физического измерения всегда отклоняется от действительного значения измеряемой величины. Это отклонение (ошибка измерения) складывается из большого числа малых случайных и систематических ошибок, допускаемых при измерении. Из курса статистики известно, что если некоторая величина x распределена с плотностью распределения p(x), то ее среднее и дисперсия определяются как

		∞	∞
		= ∫ xp( x)dx ,	Dx = ∫( x −		)2 p( x)dx . Величина σx = Dx назы-
	x			x
		−∞	−∞

вается среднеквадратичным отклонением.

Если величина распределена в соответствии с распределением Гаусса, то с вероятностью 0,68 истинное значение отличается от оценки не более чем на одну среднеквадратичную ошибку, с веро-

102

ятностью 0,95 – не более чем на две среднеквадратичных ошибки и с вероятностью 0,997 % – не более чем на 3 ошибки. Так, например, если оценка активности составила А = 5,45 ± 0,06 Бк (0,06 – среднеквадратичная ошибка), это отнюдь не означает, что ошибка измерения не превосходит 0,06 Бк; наоборот, вероятность большей ошибки значительна – 0,32. Для достоверного вывода лучше учитывать двукратное среднеквадратичное отклонение, вероятность больших отклонений уже мала – 0,05.

Обычно необходимая величина является функцией измеренных и табличных величин. Для определения среднего и погрешности

такой величины полезны следующие соотношения.
1)	Прибавление константы к случайной величине y = x + C:
	y = x +C; Dy = Dx;		σy =σx .	(6.7)
2)	Умножение случайной величины на число y = Cx:
	y =Cx;	Dy =C 2 Dx,	σy =Cσx .	(6.8)
3)	Сумма случайных величин z = x + y:
	z = x + y;	Dz = Dx + Dy +2Cov( x, y) ,		(6.9)

где Cov( x, y) = xy − x y – ковариация величин x и y; если x и y независимы, то

z = x + y; Dz = Dx + Dy; σz = σ2x +σ2y

(6.9а)

4)z = F ( x1 ,..., xn ) .

Вэтом случае разложим функцию z в ряд Тейлора в окрестностях

точки ( x , y) с точностью до первых членов:

z( x1 ,...xn ) = F (

,...

) +∑n

∂F

(

,...

) ( xi −

) , (6.10)

x1

xn

x1

xn

xi

i=1

∂x

i

тогда

= F (

,...

); Dz = ∑n

[

∂F

(

,...

)]2 Dxi +

z

x1

xn

x1

xn

i=1

∂x

i

(6.11)

n n

∂F

∂F

+∑∑

( x1

,...xn )

( x1 ,...xn ) Cov( xi , x j ),

∂x

∂x

i=1 j=1

i

j

и если x и y независимы, то

103

= F (

,...

); Dz =

n

[

∂F

(

,...

)]2 Dx ;

z

x

x

x

x

∑

1

n

∂x

i

1

n

i

i=1

(6.11а)

n

∂F

σz = ∑(

)2 σ2xi

i=1

∂xi

В частности в случае, если z = F (x, y)

z = F ( x, y); Dz = [∂F ( x , y)]2 Dx + ∂F ( x, y) 2 Dy + ∂x ∂y

+2 ∂∂Fx ( x , y) ∂∂Fy ( x, y )Cov( x, y),

иесли x и y независимы, то

z= F ( x, y); Dz = [∂∂Fx ( x, y)]2 Dx + ∂∂Fy ( x, y ) 2 Dy;

σz = (	∂F	2	2		∂F	2	2
	∂x	)	σx	+			σy .
					∂y

(6.12)

(6.12а)

Полезная

формула,

вытекающая

из

(2.11а):

если

z( x ,..., x

2

) = Const x k1

... xkn ,

то

∂z

= k

i

z

1

, и, следовательно

1

1

n

∂xi

xi

n

σ z =| zi

| ∑ki2 δ2xi

,

(6.13)

σx

i=1

где

δxi =

i

– относительная погрешность xi .

xi

Таким образом выражение для среднеквадратичного отклонения оценки активности (5б) получается следующее выражение:

σA = A δ2SППП +δY2 +δε2 +δt2 ,

(6.14)

где δx – относительная погрешность соответствующей величины. 5) Случай распределения Пуассона Известно, что распределение количества частиц в случае радио-

активного распада описывается плотностью распределения Пуас-

сона: p(n) = e−ν νn , где ν – среднее количество частиц, регистри- n!

104

руемое за время измерений t, p(n) – вероятность регистрации n частиц за время t. Для этого распределения:

n

=ν; Dn =ν; σn =ν .

(6.15)

Истинное среднее значение ν, как правило, неизвестно, поэтому его приближенно принимают равному количеству зарегистрированных частиц N. Таким образом, если в спектрометрическом канале зарегистрировано N отсчетов, то:

N

= N ; DN = N ; σN = N .

(6.16)

3.Определение положения и площади пика полного поглощения

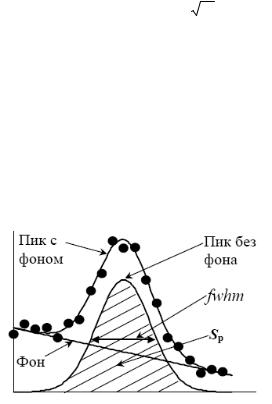
Площадью пика полного поглощения называется сумма отсчетов в пике от гамма-квантов, энергия которых полностью была поглощена детектором. Кроме этих гамма-квантов, в каналы, занятые пиком, дают также отсчет гамма-кванты с энергией большей энергии, соответствующей пику, рассеянные в детекторе. Эти гаммакванты формируют непрерывное распределение, так называемую подложку или фон под пиком полного поглощения (рис. 6.1).

Рис. 1. Пик полного поглощения с подложкой

Следовательно, для того, чтобы правильно оценить площадь пика полного поглощения, необходимо скорректировать сумму отсчетов в пике на величину подложки. Простым и достаточно точным образом это можно рассчитать по следующей формуле:

105

SППП = ∑Ni − 1

∑Ni

∑Ni

слева

+

справа

kППП =

ППП

2

kслева

kсправа

(16)

= ∑Ni −

kППП

∑Ni

−

kППП

∑Ni .

ППП

2kслева слева

2kсправа справа

Здесь слева и справа от пика полного поглощения шириной kППП

каналов выбрано соответственно kслева и kсправа каналов с фоном, а индексы «ППП» «слева» и «справа» в суммах означают суммирование по каналам пика полного поглощения, левым и правым фоновым каналам соответственно.

Согласно приведенным выше формулам:

	σS		= ∑Ni +	kППП2	∑Ni +	kППП2	∑Ni . (6.18)
		ППП		4kслева2		4kсправа2
			ППП		слева		справа

При kслева =kсправа =kфон , как это часто выбирается на практике:

σSППП = ∑Ni +	kППП2	∑Ni .	(6.18а)
	2
ППП	4kфон фон

Из (6.18) и (6.18а) хорошо видно, что наличие подложки под пиком не только затрудняет определение границ пика, но и приводит к увеличению погрешности определения площади пика. Поэтому при прецизионных низкофоновых измерениях приходится принимать комплекс всевозможных мер по снижению фона в месте расположения детектора.

4. Применение метода наименьших квадратов

4.1.Метод наименьших квадратов в случае множественных измерений

Пусть у нас имеется несколько независимых оценок одной и той же величины. Например, оценка активности нуклида, проведенная по различным пикам полного поглощения, соответствующим данному нуклиду – { Ai , σi ; i =1,..., N} , где Ai , σi , оценка и средне-

106

квадратичное отклонение соответственно. В этом случае минимизирующий функционал метода наименьших квадратов имеет вид

N

( A − A ) 2

Φ( A) =∑

i

.

(6.19)

2

i=1

σi

Поскольку Φ(А) должен иметь минимум на искомой оценке A =

,

A

N

2(

− A )

A

∂Φ ( A ) = ∑

i

= 0 ,

(6.19а)

σi2

∂A

i=1

следовательно,

N

A

N

(

− A )2

A

∑

i

∑

i

2

2

=

i=1

σi

;

σ

=

i=1

σi

,

(6.20)

A

A

N

N

1

1

∑

∑

2

2

i=1

σi

i=1

σi

в случае равноточных измерений (σi =σ=Const) получаем известные выражения:

N

N

∑Ai

∑(

− Ai )2

A

=

i=1

; σ

=

i=1

.

(6.20а)

A

N

A

N −1

4.2.Подгонка зависимостей методом наименьших квадратов

Очень часто на практике желательно перейти от экспериментально измеренной в дискретных точках зависимости одной величины от другой аппроксимации этой зависимости аналитической функцией. В области спектрометрии эту задачу необходимо решить при проведении калибровок спектрометра по энергии и эффективности – необходимо аппроксимировать на требуемом энергетическом диапазоне экспериментальные значения, полученные для ограниченного числа измерений, соответствующих энергиям имеющихся калибровочных источников.

В общем виде задача ставится так.

107

Имеется ряд измерений {xi , yi , σi ; i =1,..., N}. Из априорных со-

ображений выбирается аппроксиматор f ( x) = ∑n	a j	g j ( x) , пред-
j=0
ставляющий собой линейную комбинацию функций		gi ( x) , и тре-

буется найти набор параметров aj, на котором достигается минимум функционала

N	[ yi − f ( xi )]	2 N		[ yi −∑n	a j g j ( xi )]2
Φ(a0 ,..., an ) =∑			= ∑	j=0		. (6.21)
	σi2				σi2
i−1			i=1

Из условия равенства нулю в минимуме частных производных

∂Φ получаем систему n+1 линейных уравнений

∂ak

∂Φ	= 0, k = 0,..., n	(6.22)
∂ak

для определения параметров a0, a1,…,an.

С учетом выбранного аппроксиматора система (6.21) выглядит следующим образом:

	N	yi g k	( xi )	N	g k ( xi )	n
	∑			=∑		∑a j g j ( xi ) , k =0,...,n . (6.22а)
		σi2			σi2
	i=1			i=1		j=0

Данную систему удобнее переписать в векторном виде, дующие обозначения:

A = (Aij )= (g j

W

		a0					y1
G			a			G
		=
a				1		, y =	...	,
		...
							y N
		an					g1 ( x1 )			g n ( x1
					g0 ( x1 )				...
		) )=			g0 ( x2 )		g1 ( x2 )		...	g n ( x2
( xi
						...
							g1 ( xN )		...	g n ( xN
				g0 ( xN )
		1/ σ2				0	...	0
				1		1/ σ22
=		0					...	0
	...					...	...	...	.
		0				0	...	2
								1/ σN

введя сле-

)

) (6.23)

)

108

Тогда решение системы запишется так:

aG = ( AT WA)−1 AT W yG,

(6.24)

где AT обозначает транспонированную матрицу.

N	A A		A jk
( AT WA)ik =∑	li lk	; ( AT W ) kj =		; i,k =0,..., n . (6.25)
	2		2
l =1	σl		σ j

Доказано, что несмещенная оценка погрешности определения параметров a j

Da j =

V T WV

(( AT WA) −1 ) jj ,

(6.26)

N −n −1

n

y1 −∑a j g j ( x1 )

j=0

T

где

...

невязка

и

(V

W V ) =

V =

y N −∑n

a j g j ( xN

)

j=0

N

( yi − ∑n

a j g j ( xi ))2

= ∑

j=0

–

обобщенная (взвешенная)

сумма

σi2

i=1

квадратов невязок.

После того как оценка параметров a проведена и производится оценка аппроксиматора в произвольной точке xˆ , дисперсия оценки f (xˆ) будет равна:

	1	N	[yi − ∑n	aj g j (xi)]2
Df (xˆ) =		∑i=1	j=0		×	(6.27)
	N −n −1			σi2

×∑∑gi(xˆ)g j (xˆ)((ATWA)−1)ij.

i j

Одним из наиболее часто встречающихся случаев подгонки является подгонка полиномами g j (x) = xi. В этом случае

109

		1	x
			1
j		1	x2
A = (Aij )= (xi	)=
	...
		1	xN

...	xn
	1
...	x2n
	n
...
	xN

		N		i+k
	( AT WA)ik = ∑			xl	;		i, k = 0,..., n;
				2
		l =1		σl
		xk
	( AT W )kj =	j	; k = 0,..., n; j =1,..., N
		σ2j
	N n						k
	ai = ∑∑(( AT WA)−1 )ik						x j	y j ; i = 0,..., n
	j=1 k =0						σ2j

(6.28)

(6.29)

			n
n	1	N	(yi −∑aj g j(xi))2
f (xˆ) = ∑ai xˆi; Df (xˆ) =		∑	j=0	×	(6.30)
			2
i=0	N −n −1 i=1		σi

×∑∑ xˆixˆ j ((ATWA)−1)ij

ij

5.Калибровка спектрометра по энергии и эффективности

5.1. Калибровка по энергии

Калибровка по энергии подразумевает определение зависимости E(N), где Е – энергия гамма-квантов, N – номер канала. Ранее было показано, что теоретически номер канала пропорционален энергии, т.е. должна соблюдаться линейная зависимость

E(N) = a + b E,

(6.31)

однако на практике из-за нелинейности тракта спектрометра более хорошие результаты может дать аппроксимация параболой:

E(N) = a + b E +с E2.

(6.32)

110