Кашурников Сверхтекучест и бозе-конденсация 2008

рождения M и уничтожения , подчиняющихся следующим

коммутационным соотношениямM W MБозе:= p A

n no no n nno

M M W M M = /A

nn nnoo W nnoo nn = /( ' ( )

Таким образом, в отличие от фермионов, волновая функция симметрична по перестановкам координат и импульсов частиц. На

qs,

u s

w

s

волновую

функцию в

представлении

r

чисел заполнения

?y

M

r

r

r

rnt

nv ,rгде

nx

– числа заполнения в состоянии с импульсом

M ngsnw = zsngsn W wA

операторы

,

действуют следующим образом:

r r

r

r

n gsnwM= zsn b gsn b wA

r

r

r r

n ngsnw = sngsnw( ' (,)

Числа заполнения квантовых состояний при симметричных волновых функциях ничем не ограничены и могут иметь произвольные значения, в отличие от антисимметричных волновых функций фермионов, для которых действует принцип Паули. Функцию распределения бозе-частиц несложно получить,

рассмотрев термодинамический потенциал системы

,

каноническом ансамбле

где статистическая сумма

в большом

{ = W9|}~

невзаимодействующих частиц имеет вид

для системы

~

= •…†'€‚‡ˆ)‰`ˆ & ' (2)

~ = • €• < • ‚ƒ„v <

•

`

`ˆ

так как энергия

частиц в состоянии

равна

. Заметим, что в

(1.8)n

стоит

геометрическая прогрессия,n n

и для ее

правой

части

s

?

S s

сходимости необходимо, чтобы

†'€‚‡ˆ)

. Это условие должно

состояний

, в том числе и для

.

выполняться для всех

:

должен n

быть

химическийn

потенциал

Отсюда

находим,

что

S

?

S

= /

отрицателен:

. Суммируем геометрическую прогрессию и

статистической суммы состояния :

получаем для Š : /

{n = 9|} # W ij ‹

Š W Sn

Œ%( ' (O)

21

заполнения

•snw = WŽ{n •Š

:

Теперь можно найти средние числа

9

sn'9) = •snw = • nM nw =

( ' ( /)

Sn W Š

ijодночастичной# % W

функцией

Выражение

(1.10)

является

9

распределения Бозе – Эйнштейна.

“

•

Энергия одной частицы равна

. Полное число частиц

(1.10):n

в газе получаем, суммируя

S

= ? +

• = •

=

Q

‘ ’S

S

( ' ( )

Sn W Š

S W Š

n ij #

9

% W +>

$

ij #

9

% W

Энергия

Š

9

s = • Q

Уравнение нормировки (1.11) определяет неявно химический

потенциал

как функцию температуры

и плотности

.

бозе-газа

Q

“

S S

! = • Sn

=

‘ ’S

( ' ( +)

n

ij #

Sn

W Š

% W

+>

ij #

S W Š

% W

9

$

9

Рассмотрим случай низких температур. При низких температурах свойства бозе-газа кардинально отличаются от свойств классической системы уже тем, что основное состояние системы

при

S

= /

имеет

энергию

(т.е. все частицы сконденсированы в

Согласно нормировочному уравнению (1.11),

состояние с

!).= /

пониженииn

температуры химический потенциал

возрастает,

оставаясь отрицательным,

и достигает

значенияŠ

Š = /

при

температуре

9$, удовлетворяющей соотношению

•

'

9

“

”

'

9

Q =

$)

$)

+>

$‘ ’” • W = + +> –'* +)( ' ( *)

Здесь учтено,

что

—$“

˜œ™‚V›˜ = •'”)–'”),

–'”) – дзета-функция

™št

•'”) – гамма-функция (• # % =

Римана

(– # % = +( +),

)

V

). Из (1.13) получаем температуру (как будет

видно= •' далее,+ =

температуру> +

конденсации):

22

	+>				•					•
							= *(*
9$ = …–'* +)‰					dQe					dQe	( ' ( F)
При более низких температурах								уравнение нормировки
					хотя они$должны существовать для
(1.11) не имеет решений				,		9 : 9
	связано с тем, что в этом случае нельзя
бозе-статистики. Это		Š : /

переходить формально от суммирования к интегрированию в

(1.11). Необходимо более аккуратно учитывать член с

n

: из-за

Однако именно он

наличия множителя

он выпадает из суммы.

S

= /

S = /

температурах,

так как

именно

в

состояние

важен

при

низких

S

конденсируются все частицы. Формально из (1.11) можно

заметить,n

что при переходе к пределу

этот член расходится.

двумя способами: во-первых,

Решить

эту

проблему

можно

Š ž /

устремляя

не к

нулю, а

к некоторому

конечному малому

9 : 9

Š = /

и, во-вторых, рассчитав сначала число частиц при

значению,

Š

S \ /,

(при

$

), так как эта величина, определяемая (1.11) с

конечна:

Q'

9) “

”

9

•‡Ÿ$ =

+>

‘ ’” • W = • d9$e

' ( f)

определение

(1.13)).

Остальные

(здесь

использовано

$

частицы$

определяются из

сконденсированные в состояние

S = /

9

нормировки

•‡ $

= •$ = • ¡ W d 9 e ¢( ' ( )

9$

Таким образом, при температуре 9 = 9$ начинаетсяS =конденсация/ бозе-частиц в низшее энергетическое• состояние , и число сконденсированных частиц $ определяется степенной зависимостью (1.16). Это наблюдается на эксперименте (Андроникашвили, [12]).

23

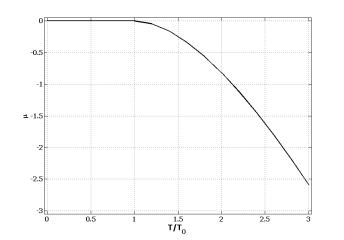
Температурная зависимость химического потенциала бозе-газа показана на рис. 1.6.

Рис. 1.6. Зависимость химического потенциала бозе-газа от температуры

Определим термодинамические величины бозе-газа в условиях

£,S \ /

¤

Š = /

¥

!

наличия конденсата (

$

). Они определяются только частицами

везде

, находим энергию

, теплоемкость

с

. Полагая

9 : 9

S S

*Q'

9) 9

Q

“

энтропию

и свободную энергию

:

! = +> $‘ ’S ij'S 9) W = F +>

–'f +) =

= /(,,/•9 d

9 e A

£ = Ž!

9$

= f!

"9 A

Ž9

£

+9

f!

¤ = ‘

9

’9 =

*9 A

+

¥ = ! W 9¤ = W * !( ' ( ,)

24

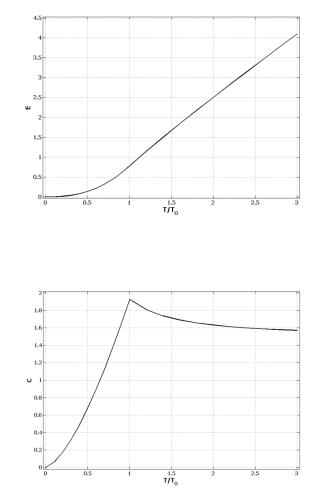
В точке 9 = 9$ все величины (1.17) непрерывны (рис. 1.7), однако производная теплоемкости испытывает9 = 9в этой точке конечный(O+• скачок, т.е. теплоемкость имеет при $ излом и равна (рис. 1.8). Таким образом, явление бозе-конденсации – фазовый переход второго рода.

Рис. 1.7. Зависимость энергии бозе-газа от температуры

Рис. 1.8. Зависимость теплоемкости бозе-газа от температуры

25

Заметим, что зависимость теплоемкости от температуры близка к наблюдаемой экспериментально в жидком9 гелии (см. рис. 1.3), а оценка критической9 температуры $ – к экспериментальному значению B.

1.5.Возбуждения в неидеальном бозе-газе. Спектр Боголюбова. Фононы и ротоны

Рассмотрим сначала качественно возможные возбуждения вовзаимодействующемž / бозе-газе в длинноволновом пределе

. В квантовой бозе-системе элементарные возбуждения должны иметь целочисленный спин, так как момент импульса всякой квантово-механической системы может меняться только на целое число. Поэтому в квантовой бозе-жидкости элементарными

возбуждениями с малыми импульсами являются обычные гидродинамические волны, т.е. фононы (квазичастицы с нулевым

спином). Таким образом, закон дисперсии возбуждений должен

где размерный	S	= § & ' ( 2)
быть линеен:	¦
	коэффициент	имеет смысл скорости звука. Число
этих возбуждений стремится§ к нулю при				, и при низких
			они практически не
температурах,	когда их число мало, и		9 ž /

взаимодействуют, их можно считатьŠ =идеальным/ бозе-газом с нулевым химическим потенциалом (число возбуждений не

фиксировано), с функцией распределения возбуждений

s' ) = ij…S¦9‰ W ( ' ( O)

Зная распределение (1.19) и закон дисперсии (1.18), можно, аналогично случаю идеального бозе-газа, рассчитать термодинамические величины жидкости при низких температурах:

26

! = Q		“			§		=	>	Q9 & ' (+/)
		‘ ’
где	'+>)	$		ij'§ 9) W				*/§
			£ = Ž! = F ! "9 A
			Ž9£		9	F!
			¤ = ‘ 9		’9 =	*9 A ' (+ )
		¥ = ! W 9¤ = W * !(

При увеличении импульса закон дисперсии отличается от линейного (1.18), и дальнейший ход зависимости определяется взаимодействием между частицами бозе-газа.

Получим закон возбуждений над основным состоянием взаимодействующего бозе-газа. Рассмотрим слабо неидеальный

бозе-газ с одинаковым взаимодействием								¨	между парами частиц,
описываемый гамильтонианом						•
= • S¦ ¦M ¦ b ¨								¦M© ¦Mª ¦« ¦t & ' (++)
			¦	+Q		¦t¦«¦ª¦©
S =		+			¦tM¦« ¦ªM¦©
							¨
где ¦			, а	взаимодействие				связано с		амплитудой
соотношением										"Q •
рассеяния		между двумя одинаковыми частицами, имеющей
величину	порядка			межчастичного				расстояния,			,

¨ = F>( ' (+*)

Боголюбов (1947 г., см. [13, 14]) показал, что для описания основного и низших возбужденных состояний удается диагонализовать гамильтониан (1.22) и получить энергетический спектр. Упростим взаимодействующую часть гамильтониана, учитывая, что в основном состоянии частицы находятся в конденсате, и ввиду слабости взаимодействия основное состояние взаимодействующего газа будет слабо отличаться от основного

27

состояния	идеального		газа,	поэтому	число частиц	над
• W •$ ¬ •$(
конденсатом будет много меньше числа конденсатных частиц •$:
•"z• -
Так как	матричные элементы			бозевских	операторов	равны
$		(см. (1.7)),	то в	(1.22) можно оставить только

взаимодействие конденсатных частиц между собой и с возбуждениями, пренебрегая взаимодействием надконденсатных частиц между собой:

y`® = ¨	¯ $M $M $ $ b •…+ ¦M $M ¦ $ b + ‚¦M $M ‚¦ $‰ br
+Q	r	¦°$	‚¦ $ $ b $		$ ¦ ‚¦‰±( ' (+F)
	b •… ¦
		M	M	M	M

¦°$

В последней сумме в (1.24) учтены процессы рождения и уничтожения пары возбуждений из конденсатаb 'W ) = /и в конденсат с сохранением суммарного импульса (это последние два члена в сумме), а также одночастичное рассеяние возбуждений на конденсатной частице (первые два члена).

Так как z•$ - , операторы $M и $ можно считать простыми числами, равными z•$. Отсюда взаимодействующая часть

		y`®	=
гамильтониана переписывается в виде
= ¨	²•$ b •$	•…+ ¦M ¦ b + ‚¦M	‚¦ b ¦M ‚¦M b ¦ ‚¦‰³( ' (+f)
+Q		¦°$

Учтем выражение для полного числа частиц:

• = •$ b + ¦°•…$ ¦M ¦ b ‚¦M ‚¦‰( ' (+ )

Выразим все числа •$ через • в (1.25),•ограничиваясь членами, содержащими не более первой степени . С учетом (1.26) и (1.25) полный гамильтониан (1.22) переписывается в виде

28

	¨•			¨•	r	M	M
	= +Q b + ¦°•$	´µ+ b					¦ b ‚¦ ‚¦‰ b
				Q ¶ … ¦
	r	¨•	M	M
		Q	… ¦	‚¦ b ¦ ‚¦‰X( ' (+,)
	b

Диагонализуем гамильтониан (1.27). Для этого введем линейные

M

преобразования операторов:

¦

=

…l¦ b ¸¦l‚¦‰A

· W ¸¦

M

M

¦

=

…l¦ b ¸¦l‚¦‰( ' (+2)

· W ¸¦

Несложно убедиться, что операторы

также удовлетворяют

коммутации. Подставив их в

бозевским

соотношениям

l

гамильтониан (1.27) и обозначив ¨•

¤ =

Q

A

b ¤A

¤¦ = +

¹¦= b ¸¦A

получим

º¦

= W ¸¦& ' (+O)

= ¤• b •

…¤¦¸¦ b ¤¸¦‰ b

•

+

¦°$

º¦

M

M

b +

º¦ »…¤¦¹¦ b +¤¸¦‰…l¦ l¦ b l‚¦l‚¦‰¼ b

¦°$

M

M

b +

¦°•$ º¦

»…+¤¦¸¦ b ¤¹¦‰…l¦ l‚¦ b l¦l‚¦‰¼( ' (*/)

Приравнивая коэффициент при недиагональном члене нулю,
находим ¸¦:			W ¤		¶( ' (* )
+¤¦¸¦ b ¤¹¦= / ½ ¸¦	= ¤	µW¤¦ b ·¤¦
29

В (1.31) перед корнем поставлен знак “

” из-за положительности

основного состояния

.

энергии возбуждений относительно

b

M

M

S = /

¤•

Подставив (1.31) в (1.30), находим окончательно:

=

+

b + ¦°•$ ¤¸¦ b + ¦°•$

·¤¦

W ¤

…l¦ l¦ b l‚¦l‚¦‰( ' (*+)

Видно, что (1.32) состоит из некоторой константы

, имеющей

жидкости,$

и энергии

смысл

энергии

основного

состояния

бозе-

!

возбуждений со спектром

!¦

, так что полная энергия системы

имеет вид

• !¦

! =

• w = !$ b

•l¦Ml¦ b l‚¦M l‚¦w = !$ b • !¦s¦ A

+

¦°$

•l¦Ml¦w

= s¦A

¦°$

!$ =

¤•

¤¸¦ A

+

b + ¦°•$

¦

¾

¨•

¨•

¦

W ¤

=

b

¶

W d

e ( ' (**)

!

= ·¤

µ

Здесь

¦ – функция распределения+

возбужденийQ

Q(1.19), имеющая

бозе-функции с нулевым химическим потенциалом. В

вид

s

§ & § = z¨•

Q& ž /Ar

предельных случаях спектр возбуждений имеет вид

!¦ =

¿ +

&

ž À( ' (*F)

При малых импульсах получаем, как и следовало§ ожидать, звуковой закон дисперсии со скоростью звука . При больших импульсах имеем спектр свободной частицы, так как взаимодействие перестает играть существенную роль.

30