
Министерство образования и науки РФ
НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ЯДЕРНЫЙ УНИВЕРСИТЕТ «МИФИ»
Р. Г. Козин
ПРОГРАММИРОВАНИЕ ЧИСЛЕННЫХ МЕТОДОВ ЛИНЕЙНОЙ АЛГЕБРЫ
Учебно-методическое пособие
Москва 2010
УДК [512.64:004.4]:519.6(07)
ББК 22.143я7+22.19я7+32.973.202-018.я7 К59
Козин Р.Г. Программирование численных методов линейной алгебры: Учебно-методическое пособие. – М.: НИЯУ МИФИ, 2010. – 128 с.
Учебное пособие знакомит с численными методами решения задач линейной алгебры. Рассматриваются алгоритмы этих методов и подробно обсуждаются вопросы их программной реализации.
Пособие предназначено для студентов группы К4-331, обучающихся по специальности «Прикладная математика и информатика», для методической поддержки лекций, практических занятий и лабораторного практикума по курсу «Специальные главы математики».
Рекомендовано к изданию редсоветом НИЯУ МИФИ
Рецензент канд. техн. наук, доцент В. В. Золотарев
ISBN 978-5-7262-1354-5 © Национальный исследовательский ядерный университет «МИФИ», 2010
Оглавление |
|
Предисловие............................................................................................. |
4 |
Введение................................................................................................... |
5 |
Глава 1. Нормы вектора и матриц, |
|
мера обусловленности матрицы.............................................. |
6 |
1.1. Норма вектора.............................................................................. |
6 |
1.2. Норма матрицы ........................................................................... |
7 |
1.3. Мера обусловленности матрицы ............................................. |
11 |
Глава 2. Методы решения систем |
|
линейных уравнений............................................................... |
15 |
2.1. Итерационные методы решения систем |
|
линейных уравнений.................................................................. |
15 |
2.2. Прямые методы решения системы линейных уравнений ...... |
30 |
2.3 Метод регуляризации для решения |
|
плохо обусловленных систем.................................................... |
59 |
Глава 3. Методы решения задачи на собственные значения............. |
64 |
3.1. Собственные значения и собственные векторы матрицы...... |
64 |
3.2. Решение частичной проблемы собственных чисел |
|
для симметричной матрицы...................................................... |
67 |
3.3. Решение задачи на собственные значения |
|
методом Данилевского.............................................................. |
75 |
3.4. Метод Крылова........................................................................... |
86 |
3.5. Определение собственных векторов в общем случае............. |
91 |
3.6. Метод вращения......................................................................... |
92 |
Глава 4. Алгоритмы для работы с полиномами............................... |
104 |
4.1. Подсчет значения полинома и деление на множители......... |
104 |
4.2. Локализация корней полинома............................................... |
106 |
4.3. Метод парабол для нахождения.............................................. |
117 |
всех корней полинома.............................................................. |
117 |
Лабораторный практикум................................................................... |
126 |
Список литературы.............................................................................. |
128 |
3
Предисловие
Впособии рассматриваются численные методы решения задач линейной алгебры. Подробно обсуждаются алгоритмы этих методов и все вопросы, связанные с их программной реализацией. Книга предназначена для поддержки курса «Специальные главы математики».
Вкниге приведены методы решения следующих задач линейной алгебры:
•определение нормы вектора и матрицы, меры обусловленности матрицы;
•нахождение решения системы линейных уравнений;
•вычисление определителя матрицы;
•определение обратной матрицы;
•нахождение максимального и минимального собственных чисел матрицы;
•нахождение характеристического многочлена матрицы;
•определение всех собственных чисел и векторов матрицы;
•выделение линейного и квадратичного полиномов из заданного полинома;
•локализация и последующее уточнение корней полинома
Каждый тематический раздел завершается несколькими вопросами и заданиями для самоконтроля. В заключении приведены темы заданий для лабораторного практикума.
В конце пособия приведен список литературы, c помощью которой читатель может расширить свои познания в области численных методов линейной алгебры и других разделов вычислительной математики.
Автор выражает благодарность канд. техн. наук, доценту В. В. Золотареву, любезно прочитавшему рукопись и сделавшему ряд ценных замечаний.
4
Введение
Методы решения задач линейной алгебры являются основополагающими в вычислительной прикладной математике, поскольку большинство реальных вычислительных задач из других разделов математики, как правило, сводятся к аппроксимирующим их задачам линейной алгебры, либо результаты линейной алгебры непосредственно используются при вычислении конкретных прикладных величин.
Наиболее востребованными задачами линейной алгебры являются следующие задачи.
1. Найти вектор х с координатами хi, i = 1÷n, являющийся решением системы линейных уравнений
Ах = b,
где A (Аij, i,j = 1÷n) – исходная матрица; b (bi, i = 1÷n) – заданный вектор правых частей системы.
2.Для заданной матрицы А вычислить определитель det(A).
3.Найти матрицу A–1, обратную заданной A, для которой выполняется матричное равенство A–1A = E, где E – единичная
матрица ( Eij = δij ).
4. Для заданной матрицы А определить собственные числа λi и соответствующие им собственные векторы xi, которые удовлетворяют матричному уравнению Ax = λx.
5. Найти корни полинома
n
Pn (x) = ∑ai xn−i = a0 xn + a1xn−1 +... + an =0 ,
i=0
выделить из полинома линейные и квадратичные множители.
5
Глава 1. НОРМЫ ВЕКТОРА И МАТРИЦ, МЕРА ОБУСЛОВЛЕННОСТИ МАТРИЦЫ
Введем понятия нормы вектора и матрицы, которые используются при «интегральной» оценке результатов операций, выполняемых над этими распределенными объектами.
1.1. Норма вектора
Норма вектора 
 x
x
 – положительная скалярная величина, вычисляемая через его компоненты xi , i =1÷n и явно или косвенно
– положительная скалярная величина, вычисляемая через его компоненты xi , i =1÷n и явно или косвенно
характеризующая его длину. Как и длина вектора, она должна удовлетворять следующим соотношениям:
|
|
x |
|
|
|
≥ 0, |
|
|
|
cx |
|
|
|
= |
|
|
|
|
|
c |
|
|
|
|
|
|
|
x |
|
|
|
, |
|
|
|
|
|
|
|
|
x + y |
|
|
|
≤ |
|
|
|
x |
|
|
|
+ |
|
|
|
y |
|
|
|
. |
(1.1) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
Приведем три способа определения нормы вектора: |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1) |
кубическая норма |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
куб |
|
= max |
|
|
|
xi |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.2) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
октаэдрическая норма |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
окт = ∑ |
|
xi |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1.3) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
3) |
сферическая норма |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
сф = |
|
∑ |
|
xi |
|
|
2 = |
|
|
|
(x, x). |
(1.4) |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
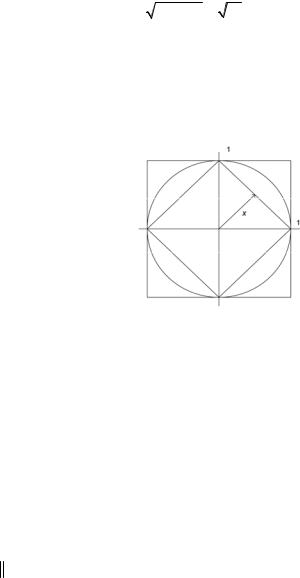
Концы множества векторов, нормы которых удовлетворяют равенствам 
 x
x
 куб =1,
куб =1, 
 x
x
 окт =1 и
окт =1 и 
 x
x
 сф =1, нарисуют в п-мерном пространстве соответственно поверхности п-мерного куба, п- мерного октаэдра и п-мерной сферы. Это обстоятельство и объясняет их название. Легко проверить, что все указанные нормы удовлетворяют трем соотношения (1.1).
сф =1, нарисуют в п-мерном пространстве соответственно поверхности п-мерного куба, п- мерного октаэдра и п-мерной сферы. Это обстоятельство и объясняет их название. Легко проверить, что все указанные нормы удовлетворяют трем соотношения (1.1).
Из рис. 1.1 видно, что между этими нормами для любого вектора х выполняются соотношения

 x
x
 окт ≥
окт ≥ 
 x
x
 сф ≥
сф ≥ 
 x
x
 куб .
куб .
6
Справедливость соотношения легко подтверждается на примере
конкретного |
вектора x =[1,2, 3], |
для которого соответствующие |
|||||||||||||||||||||
нормы равны |
|
x |
|
|
|
куб = 3 , |
|
|
|
x |
|
|
|
окт = 6 и |
|
|
|
|
x |
|
|
|
сф = 1+ 4 +9 = 14 ≈ 3,74 . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Замечание. Из равенства норм двух векторов не следует равенство самих векторов, в то время как равные векторы всегда имеют равные нормы.
Приведем алгоритмы вычисления двух норм 
 x
x
 куб и
куб и 
 x
x
 окт
окт
(поскольку они одновременно демонстрируют, как можно найти максимальное значение и сумму любой последовательности чисел).
1.norm = 0 for i =1,n
|
{ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
buf = |
|
xi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
if buf > norm then norm = buf |
|
|
|
|
|
|
|
|
|
|
||||||||
|
} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
norm = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
for i =1,n |
|
|
|
|
Рис. 1.1. Куб, октаэдр и сфера, |
|||||||||||||
|
{ |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
соответствующие уравнениям |
||||||||||
|
norm = norm + |
|
x |
|
|
|
x |
|
куб =1 , |
|
окт =1 и |
|
x |
|
сф =1 |
||||
|
|
|
|
|
|
x |
|
|
|||||||||||
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.2. Норма матрицы
Норма матрицы 
 A
A
 – положительная скалярная величина, которая устанавливает соответствие между нормами исходного вектора
– положительная скалярная величина, которая устанавливает соответствие между нормами исходного вектора 
 x
x
 и вектора
и вектора 
 Ax
Ax
 , являющегося результатом воздействия
, являющегося результатом воздействия
на исходный вектор матрицы. При этом в зависимости от критерия, используемого для нахождения нормы матрицы
Ax |
|
≤ |
|
A |
|
|
|
x |
|
, |
|
|
|
A |
|
|
|
= sup |
|
|
|
Ax |
, |
||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|||
7
определяются два вида норм: согласованная и подчиненная (наименьшая из всех согласованных).
Выведем нормы матрицы подчиненные соответственно кубической, октаэдрической и сферической нормам вектора.
1. |
|
|
|
Ax |
|
|
|
куб |
= max |
∑Aij xj |
|
≤ max |
∑ |
|
Aij |
|
|
|
|
|
|
|
|
xj |
|
|
|
|
|
≤ max |
|
xj |
|
max ∑ |
|
Aij |
|
= |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
i |
j |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
x |
|
|
|
|
|
куб |
max ∑ |
|
Aij |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
куб = max ∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
Aij |
|
. |
|
|
|
|
|
|
|
|
(1.5) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
2. |
|
|
|
|
|
|
|
|
Ax |
|
окт = ∑ |
∑Aij xj |
≤ ∑∑ |
|
Aij |
|
|
|
|
|
|
|
|
|
xj |
|
= |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
= ∑ |
|
|
xj |
|
|
|
∑ |
|
Aij |
|
|
|
≤ max ∑ |
|
Aij |
|
|
|
∑ |
|
xj |
|
|
= |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
x |
|
|
|
окт |
max ∑ |
|
Aij |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= max ∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
окт |
|
Aij |
|
. |
|
|
|
|
|
(1.6) |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
3. 
 Ax
Ax
 сф2 = (Ax, Ax) = (x, AT Ax) = …
сф2 = (Ax, Ax) = (x, AT Ax) = …
Матрица AT A симметричная и положительно определенная (так как (AT A)T = AT ( AT )T = AT A и (AT Ax, x) = (Ax, Ax) > 0 ). Поэтому она имеет полную линейно-независимую систему собственных
векторов |
xi , i =1÷n , |
а ее собственные |
числа действительные |
и |
||
положительные: Λ1 ≥ Λ2 ≥... ≥ Λn > 0 . Представим |
произвольный |
|||||
вектор х |
в виде разложения по |
этим |
векторам |
x = ∑ci xi |
и |
|
|
|
|
|
|
i |
|
подставим его в верхнее скалярное произведение |
|
|
||||
... = (∑ci xi ,∑ci AT |
Axi ) = (∑ci xi ,∑ci Λi xi ) ≤ Λ1 (∑ci xi ,∑ci xi ) = |
|||||
i |
i |
i |
i |
i |
i |
|
= Λ1 (x, x) = Λ1 
 x
x
 сф2 ,
сф2 ,
8

отсюда
A |
|
|
|
сф = Λ1 . |
(1.7) |
|
|
||||
|
|
|
Замечание. Поскольку для симметричной матрицы AT A = A2 , то
Λ1 = λ12 и 
 A
A
 сф = λ1 .
сф = λ1 .
В заключение приведем алгоритмы вычисления кубической нормы матрицы (для октаэдрической нормы в этом алгоритме необходимо поменять местами индексы в операторах цикла) и
произведения |
B = AT A , которое используется при определении |
сферической нормы матрицы |
|
1. |
norm = 0 |
for i =1, n
{
sum = 0 for j =1, n
{
sum = sum + Aij
}
if sum > norm then norm = sum
}
2.Bij = ∑AikT Akj = ∑Aki Akj
k |
k |
|
for i =1, n |
|
{ |
|
for j =1, n |
|
{ |
|
Bij = 0 |
|
for k =1.n |
|
{ |
|
Bij = Bij + Aki Akj |
|
} |
|
} |
|
} |
9
10
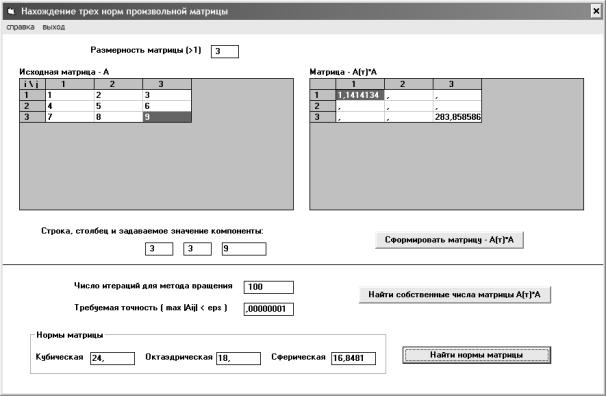
Рис. 1.2. Экранная форма программы, вычисляющей три введенные нормы матрицы
На рис. 1.2. приведен интерфейс программы, позволяющей вычислять три введенные выше нормы матрицы. Для расчета сферической нормы необходимо предварительно умножить матрицу на транспонированную, а затем найти методом вращения все собственные числа полученной таким образом симметричной положительно определенной матрицы. Собственные числа этой матрицы формируются на месте ее диагональных компонент (см. рис. 1.2). Метод вращения описывается в п. 3.6.
1.3. Мера обусловленности матрицы
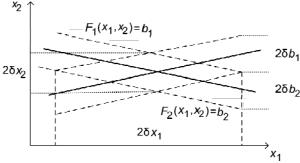
В зависимости от того, какие соотношения матрица А устанавливает между входными ( δA, δb ) и выходными (δх)
погрешностями в системе Ax = b, матрицы делятся на «плохие» и «хорошие» или в общепринятой терминологии – на плохо и хорошо обусловленные. Качественно это иллюстрируют рис. 1.3 и 1.4, на которых показаны области разброса решений для системы двух уравнений при одинаковых погрешностях в правых частях:
F1 (x) ≡ A11x1 + A12 x2 = b1;
F2 (x) ≡ A21x1 + A22 x2 = b2 .
Видно, что чем меньше угол между прямыми F1 (x) = b1 и F2 (x) = b1 , тем больше ошибки в решении системы при одних и тех
же величинах погрешностей в правых частях, а следовательно, тем хуже матрица.
Рис. 1.3. Область разброса плохо обусловленной системы
11
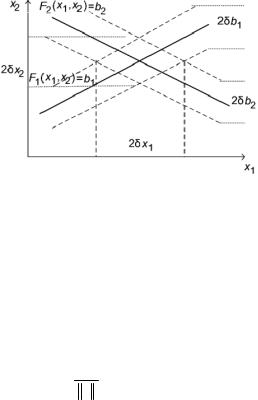
Рис. 1.4. Область разброса хорошо обусловленной системы
Качественно это можно объяснить тем, что с уменьшением угла возрастает линейная зависимость между строками матрицы, и поэтому справедлива следующая цепочка соотношений:
det(A)→ 0 , A−1 ≈ |
1 |
, δx = A−1δb ≈ |
δb |
→ ∞. |
|
det(A) |
det(A) |
||||
|
|
|
После этих качественных рассуждений перейдем к выводу количественной оценке меры обусловленности матрицы, которая устанавливает количественную зависимость между относительной
погрешностью решения 
 δxx
δxx
 системы линейных уравнений Ax = b
системы линейных уравнений Ax = b
и относительными погрешностями исходных параметров системы
|
δA |
|
|
|
и |
|
|
|
δb |
|
|
|
. Для этого запишем два матричных уравнения |
|||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
A |
|
|
|
|
|
|
|
|
b |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
(исходное и возмущенное погрешностями)
Ax = b;
(A +δA)(x + δx) = (b +δb) Ax +δAx + Aδx +δAδx = b + δb.
Вычитая первое уравнение из второго и отбрасывая в нем слагаемое второго порядка малости относительно δ, получим
Aδx = δb +δAx или |
|
|
|
|
δx = A−1 (δb +δAx) . |
|||||||||||||||||||||||||
Отсюда можно построить |
следующую цепочку неравенств |
|||||||||||||||||||||||||||||
(учтено очевидное неравенство |
|
A |
|
|
|
|
|
|
|
x |
|
|
|
≥ |
|
|
|
Ax |
|
|
|
= |
|
|
|
b |
|
|
|
): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δx |
|
|
|
|
|
|
|
≤ |
|
|
|
A−1 |
|
( |
|
|
|
δb |
|
|
|
+ |
|
|
|
δA |
|
|
|
|
|
|
|
x |
|
|
|
|
|
), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
δx |
|
|
|
≤ |
|
A−1 |
|
( |
|
|
|
δb |
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
+ |
|
|
|
δA |
|
|
|
|
|
|
|
A |
|
|
|
|
) |
≤ |
|
|
|
A |
|
|
|
|
|
|
|
A−1 |
|
|
|
|
( |
|
|
|
δb |
|
|
|
+ |
|
|
|
δA |
|
|
|
|
). (1.8) |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Последнее неравенство устанавливает для системы Ax = b количественное соотношение между входными и выходными относительными погрешностями. Присутствующий в нем
коэффициент пропорциональности |
|
ν(A) = A A−1 |
(1.9) |
называется мерой обусловленности матрицы А. Она изменяется в интервале 1 ≤ ν(A) ≤ ∞.
Замечание. Если учесть очевидное соотношение (AT A)−1 x = Λ1 x ,
где х, Λ – собственный вектор и соответствующее собственное число матрицы (AT A) , то, используя определение сферической
нормы матрицы (1.7), для меры обусловленности матрицы можно записать выражение, не требующее вычисления обратной матрицы:
ν(A) = |
Λ1 |
. |
(1.10) |
|
|||
|
Λn |
|
|
Для симметричной матрицы оно перепишется следующим образом
|
ν(A) = |
λ1 |
|
, |
|
|
|
|
λn |
|
|
||||
|
|
|
|
|
|
||
где λ1, λn – максимальное |
и минимальное |
собственные числа |
|||||
исходной матрицы А. |
|
|
|
|
|
|
|
Пример. Пусть исходная и возмущенная системы имеют вид |
|||||||
x1 −1,001x2 |
=1, |
и |
x1 −1,0015x2 =1, |
||||
−1,001x + x = 2 |
−1,0015x + x |
= 2. |
|||||
1 |
2 |
|
|
|
|
1 |
2 |
Из характеристического уравнения |
|
|
|||||
1−λ |
−1,001 |
+1,002 = 0 |
|||||
[A −λE]= |
|
1−λ |
≡ (1−λ)2 |
||||
−1,001 |
|
|
|
||||
13
легко находим собственные числа λ1 = 2,001 и λ2 = –0,001 и меру обусловленности исходной симметричной матрицы
ν(A) = λ1 = 2001.
λ2
Решения исходной и возмущенной систем, соответственно,
равны x1 = −1500,25, x2 = −1499,75 и x1 = −1000,25, x2 = −999,75 .
В итоге легко определяются следующие сферические нормы векторов и матриц
|
A |
|
|
|
≈ 2,001; |
|
|
|
δA |
|
|
|
≈ 0,0005; |
|
|
|
|
x |
|
|
|
≈1500 2 ; |
|
|
|
δx |
|
|
|
≈500 2 . |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
После этого неравенство (1.8) записывается в виде |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
δx |
|
|
|
|
= 0,333 ≤ ν(A) |
|
|
|
|
|
|
|
δA |
|
|
|
|
|
= 2001 0,00025 = 0,5 . |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
A |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Видно, что оно благополучно удовлетворяется.
Вопросы и задания для самоконтроля
1.Подсчитайте три нормы для вектора х = (1, 3, 5, 6) и сравните их между собой.
2.Для какой матрицы А справедлива следующая формула для расчета
еемеры обусловленности ν( A) = λ1 ( A) ?
λn ( A)
3.Что характеризует мера обусловленности матрицы?
4.Показать, что кубическая норма вектора удовлетворяет неравенствам (1.1).
5. Найдите двумя способами меру обусловленности матрицы
1 |
2 |
A = |
. |
2 |
5 |
6.Можно ли утверждать, что из равенства норм следует равенство векторов?
7.Составьте алгоритм нахождения кубической нормы произвольной матрицы.
14

Глава 2. МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Все существующие методы решения систем линейных уравнений x −?: Ax = b делятся на две группы: итерационные и
прямые. В первых методах точное решение можно получить после выполнения бесконечного числа операций, для вторых – конечное.
2.1.Итерационные методы решения систем линейных уравнений
2.1.1.Общая схема итерационного процесса и ее исследование
От системы Ax = b перейдем к равносильной системе
C x −τ x + Ax = b ,
где С – произвольная невырожденная матрица (C > 0), а τ > 0 – числовой параметр. Для последней матрицы можно предложить итерационную схему
C |
x(k +1) − x(k ) |
+ Ax(k ) |
= b |
|
τ |
||||
|
|
|
||
или |
|
|
||
|
x(k +1) = Bx(k ) +b , |
(2.1) |
||
где k = 0, 1, 2,... – номер итерации, х(0) – начальное приближение, которое задает пользователь,
B = E |
−τC−1 A , b |
≡ τC−1b . |
(2.2) |
В дальнейшем, задавая |
различным |
образом параметры C > 0 |
|
τ > 0, мы из схемы (2.1) получим схемы, соответствующие различным, известным итерационным методам. Сейчас же используем ее для решения следующих вопросов, касающихся всех итерационных схем: условие сходимости итерационного процесса, количественная оценка скорости сходимости, выбор критерия окончания итераций и признак расходимости итерационного процесса.
15

1. Первую проблему решает следующая теорема.
Теорема. Для сходимости процесса (2.1) необходимо и достаточно, чтобы все собственные значения матрицы В были
меньше единицы: λi (B) <1.
К сожалению, нахождение собственных значений матрицы – сама по себе не простая задача. Поэтому приведем достаточное условие сходимости, которое не требует вычисления нормы матрицы.
Следствие. Для сходимости итерационного процесса (2.1)
достаточно выполнения неравенства |
|
|
|
|
|
|
|
B |
|
|
|
|
|
<1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Доказательство. Пусть Bx = λx . |
Тогда |
|
|
|
B |
|
|
|
|
|
|
|
x |
|
|
|
≥ |
|
|
|
Bx |
|
|
|
= λ |
|
|
|
x |
|
|
|
. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
Отсюда следует неравенство 1 > |
|
|
|
B |
|
|
|
≥ |
|
λ |
|
, |
которое согласно |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
предыдущей теореме гарантирует сходимость итерационного процесса.
2. Получим оценку скорости сходимости итерационного процесса при условии 
 B
B
 <1 .
<1 .
Если 
 B
B
 <1 , то справедливо разложение
<1 , то справедливо разложение
(E − B)−1 = E + B + B2 + B3 +... .
Отсюда можно записать точное решение для задачи x = Bx +b в следующем виде
x = (E − B)−1b = (E + B + B2 + B3 +...)b . |
(2.3) |
Сдругой стороны, с учетом схемы (2.1) имеем
x(k ) = Bx(k −1) +b = B(Bx(k −2) +b) +b = B2 x(k −2) +(E + B)b =... (2.4)
=Bk x(0) +(E + B + B2 + B3 +...Bk −1 )b.
Сучетом соотношений (2.3), (2.4) можно записать
x− x(k ) = Bk [(E + B + B2 + B3 +...)b − x(0) ].
Отсюда легко выводится оценка скорости сходимости итерационного процесса в зависимости от номера итерации

 x − x(k )
x − x(k ) 
 ≤
≤ 
 B
B
 k [(1+
k [(1+ 
 B
B
 +
+ 
 B
B
 2 +
2 + 
 B
B
 3 +...)
3 +...) 
 b
b
 +
+ 
 x(0)
x(0) 
 ]
]
или, поскольку 
 B
B
 <1
<1
x − x(k ) |
|
≤ |
|
|
|
B |
|
|
|
k [ |
|
|
b |
|
|
|
+ |
|
|
|
x(0) |
|
|
|
]. |
(2.5) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
(1 |
− |
|
B |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
16
Для частного случая x(0) = b оно преобразуется к виду |
|
|||||||||||||||||||||||
|
x − x(k ) |
|
≤ |
|
|
|
B |
|
|
|
k +1 |
|
|
|
b |
|
|
|
|
|
. |
(2.6) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
(1− |
|
|
|
B |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3. Критерий окончания итераций.
Метрическое пространство векторов Rn является полным. Поэтому в качестве критерия сходимости последовательности векторов можно использовать критерий Коши: последовательность
векторов {x(k)} сходится к своему пределу x Rn тогда и только тогда, когда для любого ε > 0 существует такое K, что для всех k > K имеет место 
 x(k +1) − x(k )
x(k +1) − x(k ) 
 < ε.
< ε.
Наряду с абсолютным критерием целесообразно использовать его относительный аналог
x(k +1) − x(k ) |
< ε |
x(k +1) |
. |
(2.7) |
Кроме того, число итераций итерационного процесса следует ограничивать сверху неким максимальным числом, чтобы исключить возможное зацикливание программы (когда итерационная схема не способна обеспечить требуемую точность) или наступление аварийной ситуации в случае отсутствия сходимости процесса.
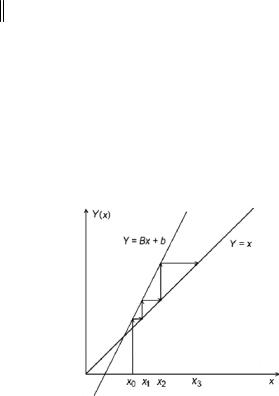
4. Итерационный процесс x(k +1) = Bx(k ) +b можно считать расходящимся, если неравенство

 x(k −1) − x(k −2)
x(k −1) − x(k −2) 
 ≤
≤ 
 x(k ) − x(k −1)
x(k ) − x(k −1) 

выполняется подряд для трех– пяти последовательных значений k. Справедливость этого утверждения для одномерного случая (n = 1) демонстрирует рис. 2.1.
Рис. 2.1. Пример расходящегося
итерационного процесса x( k+1) = Bx( k ) + b для случая п = 1
17
2.1.2. Частные итерационные схемы
Рассмотрим итерационные схемы, которые вытекают и общей схемы (2.1).
1.Метод Якоби получается при следующем выборе
параметров: τ =1, C = D . Здесь |
D – |
диагональная составляющая |
||||||||||||||||||||||||||||
исходной матрицы A = AL + D + AH , где AL , AH |
– соответственно ее |
|||||||||||||||||||||||||||||
нижняя и верхняя составляющие. Отсюда следует |
|
|
||||||||||||||||||||||||||||
B = E − D−1 (A + D + A ) = −D−1 (A + A ) . |
(2.8) |
|||||||||||||||||||||||||||||
|
|
|
L |
|
|
|
|
|
H |
|
|
|
|
|
|
|
|
|
|
|
|
L |
H |
|
||||||
С учетом очевидного вида обратной диагональной матрицы |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
D−1 = |
|
A11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
Ann |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
легко выводится покоординатная запись схемы метода Якоби |
||||||||||||||||||||||||||||||
xi(k +1) = |
1 |
|
(bi |
|
−∑Aij x(jk ) ), |
i =1,n. |
(2.9) |
|||||||||||||||||||||||
A |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
ii |
|
|
|
|
|
j≠i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Достаточное условие сходимости |
|
|
|
|
B |
|
|
|
<1 |
для |
метода |
имеет |
||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||
следующий вид |
|
|
|
|
|
|
|
|
|
Aij |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
B |
|
|
|
куб = max ∑ |
|
<1 |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
Aii |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
i |
|
j≠i |
|
|
|
|
|
|
|
|
|
|||||||||
или |
|
∑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
i |
|
|
Aij |
|
< |
|
Aii |
|
. |
|
|
(2.10) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
j≠i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Последнее означает, что для сходимости метода Якоби достаточно преобладания диагональных элементов у исходной матрицы над остальными компонентами.
2. Метод простой итерации имеет место при τ > 0, C = E . При этом
B = E −τA |
(2.11) |
покомпонентная запись схемы |
|
xi(k +1) = τbi + ∑(δij − τAij )x(jk ) , i =1,n, |
(2.12) |
j |
|
18

и достаточное условие сходимости метода
B |
|
куб |
= max ∑ |
|
δij − τAij |
|
<1. |
(2.13) |
|
|
|
|
|||||||
|
|||||||||
|
|
|
i |
j |
|
||||
|
|
|
|
|
|||||
Если матрица А симметричная и положительно определенная (ее собственные числа λ1 ≥ λ2 ≥... ≥ λn > 0 ), то для нее можно указать оптимальный параметр
0 < τ |
опт |
= |
|
2 |
|
, |
(2.14) |
λ |
+λ |
|
|||||
|
|
n |
|
||||
|
|
|
1 |
|
|
||
при котором метод простой итерации всегда сходится, причем с максимальной скоростью, так как в этом случае сферическая норма матрицы В принимает минимально возможное значение
( |
|
|
|
B |
|
|
|
|
) |
опт |
= λ1 |
−λn |
<1. |
(2.15) |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
сф |
|
λ1 |
+λn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Покажем это. |
|
|
|
B = E −τA также симметричная, и |
||||||||||
Если А – симметричная, то |
|
|||||||||||||
поэтому

 B
B
 сф = maxi 1−τλi (A) .
сф = maxi 1−τλi (A) .
Поскольку А – еще и положительно определенная матрица, то ее собственные числа λi (A) > 0 , и поэтому все функции
fi (τ) = 1−τλi (A) будут располагаться внутри зоны, очерченной
двумя ломаными линиями |
|
1− τλ1 (A) |
|
и |
|
1− τλn (A) |
|
|
(рис. 2.2). |
|||||||||||||
|
|
|
|
|||||||||||||||||||
Сферической норме |
|
|
|
B(τ) |
|
|
|
сф |
= max |
|
1− τλi (A) |
|
, как |
функция |
||||||||
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
||||||
параметра τ, на этом рисунке будут соответствовать верхние участки ломаных линий. Видно, что норма принимает минимальное значение при τопт, которое задается координатой точки пересечения ломаных линий
1− τоптλn = τоптλ1 −1 , (
 B
B
 сф)опт =1−τоптλn .
сф)опт =1−τоптλn .
Отсюда легко выводятся выражения (2.14) и (2.15). Замечание. Если матрица плохо убусловлена, то λ1 >> λn . Тогда
согласно выражению (2.15) (
 B
B
 сф)опт ≈1 и метод простой итерации для системы будет сходиться плохо.
сф)опт ≈1 и метод простой итерации для системы будет сходиться плохо.
19

|
|
|
F(t) |
|
|
|
|
|
|
|
|
|
|1-tλ1| |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|1-tλn| |
|
|
|
|
1/λ1 |
tопт |
1/λn |
t |
|
|
|
Рис. 2.2. Местоположение функций fi (τ) = 1 − τλi ( A) |
|
||||
3. |
В |
методе |
верхней |
релаксации |
принимается: |
τ > 0, |
|
C = D + τAL . В этом случае из уравнения |
|
|
|||||
|
|
|
(D +τA ) x(k +1) − x(k ) |
+ Ax(k ) = b |
|
||
|
|
|
L |
τ |
|
|
|
следует |
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
B = E −τ(D + τA )−1 A, |
|
(2.16) |
||
|
|
|
|
L |
|
|
|
|
|
Dx(k +1) |
= τb −τ( A x(k +1) + A x(k ) ) + (1− τ)Dx(k ) . |
(2.17) |
|||
|
|
|
L |
H |
|
|
|
Из матричного уравнения (2.17) легко выводится формула для |
|||||||
пересчета координат очередной итерации |
|
|
|||||
|
|
|
|
i−1 |
|
n |
|
|
xi(k +1) = (1−τ)x(k ) + τ [bi −(∑Aij x(jk +1) + |
∑ Aij x(jk ) )], |
(2.18) |
||||
|
|
|
Aii |
j=1 |
|
j=i+1 |
|
|
|
|
i =1, n. |
|
|
|
|
Воспользоваться выражением (2.16) для проверки достаточного |
|||||||
условия сходимости метода проблематично, поскольку для этого |
|||||||
требуется знание обратной матрицы. |
|
|
|
||||
Однако доказано, что если матрица А симметричная и |
|||||||
положительно определенная, то метод верхней релаксации всегда |
|||||||
сходится при 0 < τ < 2 . |
|
|
|
|
|||
Частный вариант метода верхней релаксации при τ = 1 известен |
|||||||
как метод Зейделя. |
|
|
|
|
|
||
20
В том случае выражения (2.16) и (2.18) преобразуются к виду
|
|
B = (D + A )−1 |
A , |
(2.19) |
||
|
|
|
L |
H |
|
|
|
1 |
i−1 |
n |
|
|
|
xi(k +1) = |
[bi −(∑Aij x(jk +1) |
+ ∑ Aij x(jk ) )], i =1, n. |
(2.20) |
|||
Aii |
||||||
|
j=1 |
j=i+1 |
|
|
||
2.1.3. Алгоритмическая реализация методов
Особенности реализации алгоритмов:
1.В качестве нулевого вектора берется вектор правой части матричного уравнения x(0) = b .
2.Перед запуском итерационного процесса проводится нормировка каждого уравнения путем деления его на соответствующей диагональный элемент матрицы. При этом, если встречается нулевой диагональный элемент, переменной code присваивается единичное значение и осуществляется выход из алгоритма.
3.В алгоритме автоматически отлавливается «не сходимость» итерационного процесса для заданной системы с помощью
критерия – увеличение нормы norm = |
x(k +1) − x(k ) |
в течение пяти |
|
|
куб |
|
|
последовательных итераций. Если последнее имеет место, то переменной code присваивается значение двойки и осуществляется выход из алгоритма.
4. Для окончания процесса используются два критерия: число итераций ограничено сверху заданным максимальным числом K и nort < ε, где K и ε задаются пользователем. Окончание процесса согласно одному из этих критериев соответствует code = 0. При этом в переменных K и ε возвращаются значения использованного числа итераций и достигнутой точности в оценке нормы разности соседних приближений, а в векторе х – полученное решение.
5. Используются: буферный вектор x0i , i =1,n ; переменные norm _ old , fl для хранения соответственно нормы, вычисленной на
предыдущей итерации, и числа итераций, при которых последовательно возрастает значение этой нормы.
6. exit sub обозначает выход из подпрограммы.
21

Алгоритм метода Якоби: |
xi(k +1) |
= |
1 |
(bi −∑Aij x(jk ) ), i =1, n. |
|||||||
A |
|||||||||||
|
|
|
|
|
|
|
|
|
ii |
j≠i |
|
Входные параметры процедуры: |
A, b, n, x, K, ε. |
||||||||||
code = 0, |
fl = 0, |
norm _ old = 0 |
|
||||||||
for i =1, n |
− |
нормировка уравнений, задание x0 |
|||||||||
{ |
|
|
|
|
|
|
|
|
|
|
|
x0i = bi |
|
|
|
|
|
|
|
||||
if |
|
A |
|
<10−30 (≈ 0) then |
{ code =1, |
exit } |
|||||
|
|
||||||||||
|
|
ii |
|
|
|
|
|
|
|
|
|
bi = bi / Aii |
|
|
|
|
|
|
|||||
for j =1, n |
{ if i ≠ j then Aij = Aij |
/ Aii } |
|||||||||
}
for k =1, K − цикл поитерациям
{
norm = 0
for i =1,n − цикл по уравнениям
{
xi = bi
for j =1, n { if i ≠ j then xi = xi − Aij x0 j } nt = xi − x0i
if nt > norm then norm = nt
}
if norm ≤ ε then { K = k, ε = norm, exit sub} if norm > norm _ old then fl = fl +1 else fl = 0 if fl > 5 then { code = 2, exit sub}
norm _ old = norm for i =1,n
{
x0i = xi
}
}
22
Алгоротм |
простой |
итерации: |
xi(k +1) = τbi + ∑(δij −τAij )x(jk ) , |
||||||||
|
|
|
|
|
|
|
|
|
|
|
j |
i =1,n Входные параметры процедуры: |
A, b, n, x, τ, K, ε . |
||||||||||
code = 0, |
fl = 0, |
|
norm _ old = 0 |
|
|||||||
for i =1,n |
− |
|
|
нормировка уравнений, задание x0 |
|||||||
{ |
|
|
|
|
|
|
|
|
|
|
|
x0i = bi |
|
|
|
|
|
|
|
|
|||
bi = τbi |
|
|
|
|
|
|
|
|
|||
for j =1,n |
|
|
{ if i − j then Aij |
=1−τAij else Aij = −τAij } |
|||||||
} |
|
|
|
|
|
|
|
|
|
|
|
for k =1, K |
|
− |
|
цикл поитерациям |
|||||||
{ |
|
|
|
|
|
|
|
|
|
|
|
norm = 0 |
|
|
|
|
|
|
|
|
|||
for i =1,n − |
|
цикл по уравнениям |
|||||||||
{ |
|
|
|
|
|
|
|
|
|
|
|
|
xi = bi |
|
|
|
|
|
|
|
|
||
|
for j =1,n { xi = xi − Aij x0 j } |
|
|||||||||
|
nt = |
|
xi |
− x0i |
|
|
|
|
|||
|
|
|
|
|
|
||||||
|
if nt > norm then norm = nt |
|
|||||||||
} |
|
|
|
|
|
|
|
|
|
|
|
if norm ≤ ε then { K = k, ε = norm, exit sub} |
|||||||||||
if |
norm > norm _ old then fl = fl +1 else fl = 0 |
||||||||||
if |
fl > 5 then |
|
{ code = 2, exit sub} |
||||||||
norm _ old = norm |
|
|
|||||||||
for i =1,n { x0i |
|
= xi } |
|
|
|||||||
} |
|
|
|
|
|
|
|
|
|
|
|
Алгоритм метода верхней релаксации: |
|||||||||||
|
|
|
|
|
|
|
τ |
|
i−1 |
|
n |
xi(k +1) = (1−τ)xi(k ) |
+ |
|
|
[bi −(∑Aij x(jk +1) |
+ ∑ Aij x(jk ) )], i =1, n. |
||||||
|
Aii |
||||||||||
|
|
|
|
|
|
|
j=1 |
|
j=i+1 |
||
23

Входные параметры процедуры: A, b, n, x, τ, K, ε . Используются буферные переменные: τ1, buf , nt .
code = 0, |
fl = 0, norm _ old = 0, |
τ1 =1 − τ |
|||||
for i =1, n |
− |
нормировка уравнений, задание x0 |
|||||
{ |
|
|
|
|
|
|
|
xi = bi |
|
|
|
||||
if |
|
A |
|
<10−30 |
(≈ 0) then { code =1, |
exit } |
|
|
|
||||||
|
|
ii |
|
|
|
|
|
bi = τbi |
/ Aii |
|
|
||||
for j =1, n |
{ if i ≠ j then Aij = τAij / Aii } |
||||||
}
for k =1, K − цикл по итерациям
{
norm = 0
for i =1, n − цикл по уравнениям
{
buf = τ1xi +bi
for j =1, n { if i ≠ j then buf = buf − Aij x j } nt = buf − xi
xi = buf
if nt > norm then norm = nt
}
if norm ≤ ε then { K = k, ε = norm, exit sub}
if |
norm > norm _ old then |
fl = fl +1 else fl = 0 |
if |
fl > 5 then { code = 2, |
exit sub} |
norm _ old = norm
}
Была написана программа, которая позволяет применить любой итерационный метод для решения заданной пользователем системы.
24
На рис. 2.3 и 2.4 приведены формы этой программы на начальной и конечной стадиях решения системы линейных уравнений методом верхней релаксации. Чтобы матрицу системы сделать симметричной и положительно определенной систему следует умножить на исходную транспонированную матрицу. Если система не является плохо обусловленной, то такое преобразование обеспечит сходимость итерационного процесса. Для запуска выбранного итерационного метода необходимо задать параметр τ, максимальное число итераций и требуемую точность
ε > 
 xk − xk −1
xk − xk −1 
 . По окончанию итерационного процесса в таблице
. По окончанию итерационного процесса в таблице
выдается решение и невязка ( δ = b − Axk ).
Замечание. В принципе, в качестве критерия окончания итерационного процесса можно было бы использовать условие

 δ
δ
 =
= 
 b − Axk
b − Axk 
 < eps . Этот критерий является более качественным,
< eps . Этот критерий является более качественным,
но на каждой итерации он потребует значительного объема дополнительных операций. К тому же, как видно из таблицы на рис. 2.4., применяемый критерий обеспечивает выполнение и этого критерия.
С помощью программы было проведено исследование сходимости методов простой итерации и верхней релаксации для модельной системы (см. таблицу на рис. 2.3). Результаты исследования представлены в табл. 2.1 и 2.2.
Для преобразованной системы метод Якоби также сходится. При этом ее решение определяется с заданной точностью за 1895
итераций. Заметим, что в этом случае для матрицы B = |
0 |
1,4 |
||||||||
|
|
|||||||||
|
|
|
|
|
|
|
|
|
0,7 |
0 |
(получена с учетом (2.8)) имеем λ1,2 = ±0,99 <1 < |
|
|
|
B |
|
|
|
куб |
=1,4 , т.е. |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|||||
«необходимое и достаточное условие» выполнено, а «только достаточное» – нет.
Сравнивая все полученные результаты, можно сделать вывод, что для выбранной модельной системы среди всех итерационных методов метод верхней релаксации имеет наиболее высокую абсолютную скорость сходимости. Естественно этот вывод не распространяется на все системы.
25

26
Рис. 2.3. Задание исходной системы уравнений
27
Рис. 2.4. Результаты после окончания итерационного процесса. Система была предварительно умножена на исходную транспонированную матрицу

Таблица 2.1
Зависимость предельного числа итераций от параметра τ (при ε = 0,0000001) для метода верхней релаксации
τ |
1 |
1,25 |
1,5 |
1,75 |
1,8 |
1,85 |
1,86 |
1,87 |
Итерация |
621 |
397 |
233 |
77 |
75 |
99 |
109 |
расходится |
Таблица 2.2
Зависимость предельного числа итераций от параметра τ |
||||||||
|
(при ε = 0,0000001) для метода простой итерации. |
|||||||
τ |
0.01 |
0,02 |
0,04 |
0,05 |
0,06 |
0,066 |
0,0665 |
0,067 |
итерации |
5905 |
3310 |
1733 |
1419 |
1204 |
1105 |
1359 |
расходится |
Примечание: в данном случае для модельной системы имеем: λ1 = |
||||||||
= 29,866, |
λ2 = 0,1339, τопт = 0,066. |
|
|
|
|
|||
Характер зависимости, зафиксированной в табл. 2.2, хорошо |
||||||||
объясняет рис. 2.5. |
|
|
|
|
|
|
||
Рис. 2.5. Местоположение функций |
fi (τ) = 1 − τλi ( A) |
и τопт |
для метода |
|||||
|
|
|
|
простой итерации |
|
|
|
|
28
В качестве второго примера рассмотрим систему
|
1 |
0,2 x1 |
|
1 |
|
||
|
|
1 |
|
|
= |
|
. |
0,3 |
x2 |
|
2 |
||||
Результаты, полученные с помощью программы для данной системы, приведены в табл. 2.3.
Таблица 2.3
Значения оптимального значения параметра τ и число итераций,
использованное для получения решения системы с точностью 
 xk − xk -1
xk − xk -1 
 < ε = 0, 0000001
< ε = 0, 0000001
Метод |
τопт |
Число итераций |
|
(для ε = 0,0000001) |
|||
|
|
||
Якоби |
- |
12 |
|
Простой итерации |
0,95 |
12 |
|
Верхней релаксации |
1.05 |
6 |
Вопросы и задания для самоконтроля
1.Почему для окончания итерационного процесса необходимо использовать два (какие) критерия?
2.Запишите выражение для оценки скорости сходимости итерационного процесса. При каком условии оно получено?
3.Почему последовательное увеличение значений нормы 
 x(k ) − x(k −1)
x(k ) − x(k −1) 

при трех последовательных значениях k можно считать признаком расходимости итерационного процесса?
4.Чем принципиально отличается программная реализация метода верхней релаксации от остальных методов?
5.Какие две задачи решает предварительная нормировка системы перед запуском итерационного процесса?
6.Почему по окончании итерационного процесса желательно возвращать пользователю число использованных итераций и значение нормы разности двух соседних приближений?
7.Составьте алгоритм решения системы Ax = b методом Зейделя.
29

2.2.Прямые методы решения системы линейных уравнений
2.2.1. Метод исключения Гаусса
В методе Гаусса исходная система Ax = b, начиная с левого столбца, путем (п–1)-го последовательного преобразования приводится к системе с верхней треугольной матрицей, Решение последней находится элементарно.
Приведем формулы, по которым выполняется k-е преобразование. К данному моменту текущая расширенная (к матрице добавлен столбец, состоящий из компонент вектора b) матрица исходной системы имеет следующей вид
|
A |
− |
A |
− |
A |
− |
A |
|
|
|
|
11 |
|
1k |
|
1 j |
|
1n+1 |
|
|
|
|
0 |
− |
− |
− |
− |
− |
− |
|
|
|
|
0 |
0 |
Akk |
− |
Akj |
− |
Ak n+1 |
|
....k |
|
|
0 |
0 |
− |
− |
− |
− |
− |
|
|
(2.21) |
A(k −1) = |
|
|
||||||||
|
0 |
0 |
A |
− |
A |
− |
A |
|
|
....i |
|
|
|
ik |
|
ij |
|
i n+1 |
|
||
0 |
0 |
− |
− |
− |
− |
− |
|
|
||
|
|
|
|
|||||||
|
0 |
0 |
A |
− |
− |
− |
A |
+1 |
|
|
|
|
|
nk |
|
|
|
n n |
|
|
|
При k-ом преобразовании в матрице A(k–1) необходимо обнулить все компоненты k-го нижнего подстолбца, начиная с компоненты Ak+1k. Последнее осуществляется путем вычитания из i-й строки
компонент k-й строки, умноженной на |
Aik |
: |
|
A |
|||
|
|
||
|
kk |
|
Aij = Aij − Aik Akj , Akk
i = (k +1)...n, j = k...(n +1).
Алгоритм этой операции представлен на схеме
30
for i = (k +1), n |
|
|||
{ |
Aik |
|
|
|
buf = |
|
|
||
A |
|
|||
|
|
|||
|
kk |
(2.22) |
||
for j = k,(n +1) |
||||
|
||||
{ |
|
|
|
|
Aij |
= Aij −buf * Akj |
|
||
} |
|
|
|
|
}
Замечания.
1. Легко проверить, что преобразование (2.22) эквивалентно матричной операции M (k ) A(k −1) , где матрица M (k ) имеет вид
|
|
|
|
1 |
0 |
− |
|
|
|
|
|
||||
|
|
|
|
0 |
− |
− |
|
|
M (k ) = |
|
0 |
− |
1 |
||
|
|
0 |
− |
M((kk+)1)k |
|||
|
|
|
|
||||
|
|
|
|
0 |
− |
− |
|
|
|
|
|
0 |
− |
M (k ) |
|
|
|
|
|
||||
|
|
|
|
|
|
nk |
|
|
|
(k −1) |
|
|
|
||
где |
Mik(k ) = − |
Aik |
. |
|
|
|
|
(k −1) |
|
|
|
||||
|
|
A |
|
|
|
|
|
|
|
kk |
|
|
|
|
|
− |
0 |
|
|
||
− |
0 |
|
− |
0 |
|
− |
0 |
, |
|
||
− |
0 |
|
− |
1 |
|
|
||
|
|
|
Аналогично, операцию приведения матрицы к верхней треугольной можно представить в следующем матричном виде
A(n−1) = M (n−1) ...M (1) A.
2. Поскольку нулевая нижняя подматрица в дальнейших операциях не используется, то нет необходимости ее явно обнулять. Исходя из этого в алгоритме (2.22) внутренний цикл можно начинать с k + 1.
Поместив последовательность операций (2.22) внутрь цикла по
полному числу преобразований |
|
for k =1,(n −1) { (2.22) } , |
(2.23) |
получим алгоритм, приводящий исходную систему уравнений к эквивалентной системе с верхней треугольной матрицей.
Для уменьшения влияния ошибок округления и повышения устойчивости работы алгоритма (2.23) в нем перед началом
31

очередного преобразования необходимо выполнять процедуру «выбора ведущего элемента».
Задачи этой процедуры:
-поставить на место k-й строки строку из оставшихся нижних с максимальным по модулю элементом в k-ом нижнем подстолбце;
-проверить, что найденный максимальный элемент не равен нулю (матрица невырожденная);
-осуществить подсчет определителя исходной матрицы.
При вычислении определителя учитывается, что:
1)определитель треугольной матрицы равен произведению ее диагональных компонент;
2)значение определителя не изменяется, если к его строке прибавить другую строку, умноженную на произвольный коэффициент
A11 |
A12 |
= A11 |
(A22 |
+λA12 ) − A12 (A21 + λA11 ) = |
|
A21 +λA11 |
A22 + λA12 |
||||
|
|
|
=A11 A22 + λA11 A12 − A12 A21 −λA11 A12 = A11 A22 − A12 A21;
3)при перестановке строк (или столбцов) матрицы знак определителя меняется на противоположный
A21 |
A22 |
= A A |
− A A |
= (−1)(A A |
− A A ); |
||||
A11 |
A12 |
21 |
12 |
11 |
22 |
11 |
22 |
21 |
12 |
|
|
|
|
|
|
|
|
||
4) умножение всех компонент строки/столбца матрицы на число приводит к умножению определителя этой матрицы на то же число
|
λA11 |
λA12 |
|
= λA A |
−λA A |
= λ( A A |
− A A ). |
||||
|
|
||||||||||
|
A21 |
A22 |
|
11 |
22 |
12 |
21 |
11 |
22 |
12 |
21 |
|
|
|
|
|
|
|
|
|
|
||
Алгоритм процедуры выбора ведущего элемента приведен на схеме (2.24). Здесь nul – переменная для хранения машинного нуля, используемого для проверки действительных чисел на нуль
(обычно nul ≤10−10 и может корректироваться пользователем для фильтрации уровня ошибок округления, возникающих в процессе вычисления).
32

det =1 (начальная инициализация перед запускомцикла (2.23)) − − процедура − −
k max = k
Amax = Akk if k < n then
{
for i = (k +1), n
{
Amod = Aik
if Amod > Amax then
{
|
|
Amax = Amod |
|
||
|
|
k max = i |
|
||
|
} |
|
|
|
|
} |
} |
|
|
|
|
|
|
|
|
|
|
if |
|
Amax |
|
< nul (≈ 0) then |
|
|
|
|
|||
{ |
|
det = 0 (матрица вырожденная) |
|
||
|
|
|
|||
} |
|
выходиз процедуры |
|
||
|
|
|
|
|
|
if |
k max ≠ k then |
|
|||
{ |
|
for j = k,(n +1) (переставляем строки) |
|
||
|
|
|
|||
|
{ |
|
|
(2.24) |
|
|
|
buf = Akj |
|||
|
|
Akj = A(k max) j |
|
||
|
|
A(k max) j = buf |
|
||
}
det = −det
}
det = det* Akk (вычислениеопределителя)
Замечание. Перестановка i и j строк эквивалентна матричной операции
T(i, j)A,
где
33
|
|
i |
|
j |
|
|
1 |
0 |
0 |
0 |
0 |
0 |
|
|
1 |
0 |
0 |
0 |
|
|
0 |
0 |
|
||||
|
|
|
|
|
|
i |
T (i, j) = 0 0 0 0 1 0 |
||||||
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
0 |
j |
|
0 |
0 |
0 |
0 |
|
|
0 |
1 |
|
||||
|
|
|
|
|
|
|
– матрица перестановок (на примере матрицы 6×6 и i = 3, j = 5 ).
Она обладает следующими свойствами:
1. Матричная операция T(i, j)A переставляет строки, например:
0 |
1 A11 |
A12 |
|
A21 |
A22 |
|
1 |
0 A A |
|
= A A |
. |
||
|
21 |
22 |
|
11 |
12 |
|
2. |
Матричная операция AT(i, j) переставляет столбцы, например, |
|||||||
|
A11 |
A12 0 1 |
A12 |
|
A11 |
|
||
|
A A |
1 |
0 |
= A A |
. |
|||
|
21 |
22 |
|
22 |
21 |
|
||
3. |
T (i, j)T (i, j) = E , например, |
|
|
|
|
|
||
|
|
0 |
1 0 1 1 |
0 |
|
|
||
|
|
|
|
|
= |
. |
|
|
|
|
1 |
0 1 |
0 0 |
1 |
|
|
|
После приведения системы уравнений к системе с треугольной матрицей
A11x1 + |
... |
+A1i xi + |
... |
+A1 j xj + |
... |
= A1(n+1) |
|
|
... |
... |
... |
... |
... |
|
|
Aii xi + |
... |
+Aij xj + |
... |
= Ai(n+1) |
|
|
|
|
... |
... |
... |
|
|
|
|
|
Ann xn |
= An(n+1) |
(2.25)
легко записать алгоритм решения последней (учтено, что правые части уравнений хранятся в дополнительном столбце расширенной матрицы Ai(n+1)):
34
if |
|
Ann |
|
|
< nul then {det = 0, exit sub} else det = det* Ann |
|
|||||
|
|
|
|||||||||
x |
|
= A |
|
n(n+1) |
|
|
|
||||
n |
|
|
|
|
Ann |
|
|
|
|||
|
|
|
|
|
|
|
|
||||
for i = |
(n −1),1 step = −1 |
(2.26) |
|||||||||
{ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
xi = |
|
(Ai(n+1) − ∑ Aij xj ) |
|
||||||
|
|
|
Aii |
|
|||||||
} |
|
|
|
|
|
|
|
j=(i+1) |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Здесь первый условный оператор завершает проверку матрицы и подсчет значения определителя.
2.2.2. Метод оптимального исключения Гаусса–Жордана
В отличие от метода Гаусса в данном методе исходная система Ax = b с помощью n последовательных преобразований сводится к системе с единичной матрицей, решение которой располагается на месте правого крайнего столбца расширенной матрицы (добавлен столбец, состоящий из компонент вектора b) преобразованной системы.
Приведем формулы, по которым выполняется k-е преобразование. К данному моменту текущая расширенная матрица исходной системы имеет следующей вид
1 |
− |
A1k |
− |
A1 j |
− |
A1n+1 |
|
|
||
|
− |
− |
− |
− |
− |
− |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
− |
Akk |
− |
Akj |
− |
Ak n+1 |
....k |
||
A(k −1) = − |
− |
− |
− |
− |
− |
− |
|
|
|
|
|
0 |
− |
A |
− |
A |
− |
A |
|
|
....i |
|
|
|
ik |
|
ij |
|
i n+1 |
|
||
− |
− |
− |
− |
− |
− |
− |
|
|
||
|
|
|
|
|||||||
|
0 |
− |
A |
− |
− |
− |
A |
+1 |
|
|
|
|
|
nk |
|
|
|
n n |
|
|
|
Первоначально компонента матрицы Akk приводится к единице,
путем деления k-й правой подстроки на компонент Akk: |
|
|||
A = |
Akj |
, |
j = k...(n +1). |
(2.27) |
|
||||
kj |
Akk |
|
|
|
|
|
|
|
|
|
|
|
|
35 |

Затем обнуляются все остальные компоненты k-го столбца расширенной матрицы, путем вычитания из каждой i-й строки k-й строки, умноженной на Aik:
Aij = Aij − Aik Akj , i =1...n,i ≠ k; j = k...(n +1). |
(2.28) |
Замечание. Легко проверить, что преобразования матрицы (2.27)
и (2.28) эквивалентно матричной операции L(k ) A(k −1) , где A(k–1) – исходная матрица после (k – 1)-го преобразования, а матрица L(k) имеет вид (отличается от единичной матрицы, размерности n×n, только k-ым столбцом):
|
|
|
|
1 |
− |
L(k ) |
− |
0 |
|
|
|
|
|
|
|
|
|
1k |
|
|
|
|
|
|
|
|
|
− |
− |
− |
− |
− |
|
|
|
|
|
|
L(k ) = |
0 |
− |
L(k ) |
− |
0 |
, |
(2.29) |
|
|
|
|
|
|
|
kk |
|
|
|
|
|
|
|
|
|
− |
− |
− |
− |
− |
|
|
|
|
|
|
|
0 |
0 |
L(k ) |
− |
1 |
|
|
|
|
|
|
|
|
|
nk |
|
|
|
|
|
где L(k ) = − |
A(k −1) |
|
i =1, n, i ≠ k, |
|
L(k ) = |
1 |
|
|
|
|
|
ik |
, |
|
|
|
. |
|
|||||
A(k −1) |
|
A(k −1) |
|
||||||||
ik |
|
|
|
|
ik |
|
|
|
|||
|
kk |
|
|
|
|
|
kk |
|
|
|
|
Приведем алгоритм, реализующий данный метод:
det =1 (переменная для хранения значения определителя) for k =1,n
{
вызов процедурывыбора ведущего элемента for j = k +1,n +1
{
Akj = Akj Akk
}
{for i =1, n (2.30)
if i ≠ k then
{
for j = k +1,n +1
{
Aij = Aij − Aik Akj
}
}
}
}
36

Здесь:
1)в пределах каждого k-го преобразования k-й столбец явно не обрабатывается, поскольку он в последующих преобразованиях не используется;
2)каждое очередное преобразование матрицы предваряется процедурой выбора ведущего элемента, которая приведена ниже. Переменная det используется процедурой выбора ведущего элемента для хранения значения определителя.
k max = k
Amax = Akk if k < n then
{
for i = (k +1),n
{
Amod = Aik
if Amod > Amax then
|
{ |
|
|
= Amod |
|||
|
|
|
Amax |
||||
|
|
|
k max |
=i |
|||
|
} |
|
|
|
|||
} |
} |
|
|
|
|
||
|
|
|
|
|
|
||
if |
|
Amax |
|
< nul (≈ 0) then |
|||
|
|
||||||
{ |
|
det |
= 0 (матрица вырожденная) |
||||
|
|
||||||
} |
|
выходиз процедуры |
|||||
k max ≠ k then |
|||||||
if |
|||||||
{ |
|
for |
j = k,(n +1) (переставляемстроки) |
||||
|
|
||||||
|
{ |
|
|
|
|
||
|
|
buf = Akj |
|
||||
|
|
|
Akj = A(k max) j |
||||
|
} |
A(k max) j =buf |
|||||
|
= −det |
|
|||||
|
|
det |
|
||||
}
det = det* Akk (вычислениеопределителя)
Здесь nul – переменная для хранения машинного нуля, используемого для проверки действительных чисел на нуль
37
(обычно nul ≤10−10 и может корректироваться пользователем для фильтрации уровня ошибок округления, возникающих в процессе вычисления).
Программа, использующяя метод оптиамльного исключения, приведена в п. 2.2.4.
2.2.3.Нахождение обратной матрицы методом оптимального исключения Гаусса–Жордана
Полное преобразование матрицы методом оптимального исключения может быть записано в матричном виде
L(n)T (n) ...L(1)T (1) A = E,
из которого следует матричная форма нахождения обратной матрицы (так как по определению A−1 A = E )
A−1 = L(n)T (n) ...L(1)T (1) E, |
(2.31) |
где T(i) – матрица перестановок при i-ом преобразовании, а L(i)
задано (2.29).
Согласно выражению (2.31), если исходную матрицу A дополнить справа единичной матрицей E размерности n×n, то в качестве алгоритма нахождения обратной матрицы можно использовать алгоритм (2.30), заменив в нем правые пределы циклов с n + 1 на n + n. При этом ту же замену необходимо выполнить и в процедуре выбора ведущего элемента (2.24) при перестановке строк.
В противовес сказанному, можно предложить более экономичный (по размеру используемой памяти и количеству операций) алгоритм нахождения обратной матрицы. В нем выбор ведущего элемента осуществляется в k-й подстроке с перестановкой соответствующих столбцов. В этом случае полное преобразование исходной матрицы будет записываеться в следующем матричном виде
L(n)...L(1) AT(1)...T(n) =E.
Отсюда последовательно получаем
38
AT(1)...T(n) =(L(n)...L(1) )−1E
(AT(1)...T(n) )−1 =(L(n)...L(1) )E
(T(1)...T(n) )−1 A−1 =(L(n)...L(1) )E
A−1 =(T(1)...T(n) )(L(n)...L(1) )E
Таким образом, если единичную матрицу подвергнуть тем же преобразованиям (кроме перестановки столбцов), что и матрицу А, то для окончательного построения обратной матрицы из преобразованной единичной матрицы необходимо в последней переставить между собой строки с номерами, которые соответствуют номерам переставленных в процессе преобразования столбцов, но в обратной последовательности. Естественно, номера переставляемых столбцов предварительно должны быть сохранены в двумерном вспомогательном массиве.
Обсудим детали оптимального алгоритма расчета обратной матрицы. Обозначим соответствующие матрицы после (k – 1)-го преобразования
A(k−1) =L(k−1)...L(1) AT(1)...T(k−1) ,
Они имеют вид
|
|
1 |
− |
0 |
(k−1) |
|
|
A1k |
|||
|
|
− |
− |
− |
|
|
− |
||||
|
0 |
− |
1 |
A(k−1) |
|
A(k−1) = |
|
|
|
k−1k |
|
|
0 |
− |
0 |
Akk(k−1) |
|
|
− |
− |
− |
− |
|
|
|
|
− |
0 |
A(k−1) |
|
0 |
||||
|
|
|
|
|
nk |
|
|
(k−1) |
− |
(k−1) |
|
|
B11 |
B1k−1 |
|||
|
|
|
− |
− |
− |
(k−1) |
B(k−1) |
− |
B |
||
B |
= |
(k−1) |
− |
(k−1) |
|
|
B1k |
Bkk−1 |
|||
|
|
|
− |
− |
− |
|
B |
|
− |
B |
|
|
|
(k−1) |
|
(k−1) |
|
|
|
n1 |
|
nk−1 |
|
B(k−1) =L(k−1)...L(1)E.
−A(k−1)
−1−n
−Ak(k−1−n1) ,
−Akn(k−1)
−−
−A(k−1)
0 |
− |
|
0 |
||
− |
− |
− |
0 |
− |
0 |
1 |
− |
. |
0 |
||
− |
− |
− |
0 |
− |
|
1 |
||
|
|
|
39
Обратим внимание на следующие обстоятельства.
1.В первой матрице левая часть, а во второй правая совпадают с фрагментом единичной матрицы, причем эти фрагменты таковы, что дополняют друг друга до полной единичной матрицы.
2.В процессе k-го преобразования в первой матрице k-й столбец переходит в k-й столбец единичной матрицы (поскольку он в дальнейшем не используется, то его явно можно не обрабатывать),
аво второй матрице появляется k-й столбец, отличный от k-го столбца единичной матрицы.
Все это позволяет сделать вывод, что обе матрицы можно хранить на месте исходной и во время k-го преобразования обрабатывать по единым формулам (2.32), которые получены в
результате обобщения матричных операций A(k) =L(k) (A(k
B(k ) = L(k ) B(k −1) :
выбор ведущего элемента в к −ой правой подстроке(≠ 0) |
||||||||||
A = A − |
Aik Akj |
i, j =1, n; i ≠ k, j ≠ k |
||||||||
|
||||||||||
ij |
|
ij |
Akk |
|||||||
|
|
|
|
Aik |
||||||
A |
= − |
i =1, n; i ≠ k |
||||||||
|
|
|
||||||||
ik |
|
|
AAkk |
|
|
|||||
|
|
|
|
|||||||
A |
= |
|
|
kj |
j =1, n; j ≠ k |
|||||
|
|
|
|
|
|
|||||
kj |
|
|
Akk |
|
|
|||||
|
|
|
|
|||||||
A |
= |
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
kk |
|
|
Akk |
|
|
|||||
|
|
|
|
|||||||
−1)T(k) ),
(2.32)
Теперь приведем оптимальный алгоритм в развернутом виде (если возвращается нулевое значение определителя матрицы, то матрица – вырожденная или плохо обусловлена):
det =1, m = 0 (инициализация переменных) for k =1, n
{
вызов процедуру выбора ведущего элемента в подстроке (см. ниже)
for i =1, n
{
40

if i ≠ k then
{
|
A = − |
Aik |
|
|
|
|
||
|
|
|
|
|
||||
|
ik |
|
Akk |
|
|
|
||
|
for |
|
|
|
|
|||
|
j =1,n |
|
|
|
||||
|
{ |
|
|
|
|
|
|
|
|
if |
j ≠ k then |
{ Aij = Aij + Aik Akj } |
|||||
} |
} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
} |
j =1, n |
|
|
|
||||
for |
|
|
|
|||||
{ |
|
|
|
|
|
Akj |
|
|
if |
j ≠ k then { A |
= |
} |
|||||
|
||||||||
|
|
|
|
kj |
|
Akk |
||
} |
|
|
|
|
|
|||
Akk = 1 Akk
}
вызов процедуры, переставляющей строки в обработанной матрице(см. ниже)
Алгоритм процедуры выбора ведущего элемента. Здесь для хранения номеров переставляемых столбцов используется массив Mij , i =1,2; j =1, n , а в переменной т хранится число выполненных
перестановок:
k max = k
Amax = Akk if k < n then
{
for j = (k +1), n
{
Amod = Ajk
if Amod > Amax then
{
Amax = Amod k max = j
}
}
41
} |
|
|
< nul (=1E−30 ≈ 0) then |
||
if |
|
Amax |
|||
{ |
|
det = 0 (матрица вырожденная) |
|||
|
|
||||
} |
|
выходиз процедуры |
|||
k max ≠ k then |
|||||
if |
|||||
{ |
|
for i =1, n (переставляем столбцы) |
|||
|
|
||||
|
{ |
|
= A |
||
|
|
buf |
|||
|
|
A = A ik |
|||
|
|
ik |
ik max |
||
|
|
Aik max = buf |
|||
|
} |
|
|
||
|
|
det = −det |
|||
|
|
m = m + |
1 |
||
|
|
M1m = k |
|
||
} |
|
M 2m = k max |
|||
|
|
|
|
||
det = det* Akk (вычисление определителя)
Процедура, переставляющая строки в преобразованной матрице
if m = 0 then выходиз процедуры
for l = m,1 step = −1 (переставляемстроки в обратном порядке)
{
m1 = M1l m2 = M2l for j =1,n
{
buf = Am1 j
Am1 j = Am2 j
Am2 j = buf
}
}
В заключение в качестве примера приведем экранную форму программы (рис. 2.6), которая для введенной матрицы рассчитывает ее определитель (использованы описанные выше алгоритмы) и обратную матрицу. Пользователь последовательно задает размерность матрицы и вводит значения ее компонент (выбирает ячейку в
42
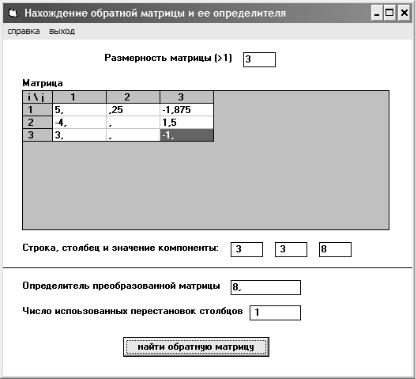
таблице, вводит значение компоненты в соответствующем текстовом поле и кнопкой ENTER на клавиатуре возвращает это значение в таблицу). После «кликания» управляющей кнопки «найти обратную матрицу» программа на месте исходной матрицы формирует рассчитанную обратную матрицу. Одновременно выдается значение определителя исходной матрицы и число использованных перестановок столбцов.
Рис. 2.6. Экранная форма программы, на которой сформирована обратная
0 2 3
матрица для исходной матрицы 4 5 00 6 8
43
Вопросы и задания для самоконтроля
1.В чем суть метода исключения Гаусса?
2.Для каких целей в прямых методах используется процедура «выбора ведущего элемента»?
3.Запишите алгоритм для k-го преобразования исходной матрицы в методе Гаусса.
4.Запишите алгоритм нахождения решения системы с нижней треугольной матрицей.
5.Чем метод Гаусса отличается от оптимального метода исключения Гаусса-Жордана?
6.Что такое матрица перестановок? Каковы ее свойства?
7.Напишите алгоритм, который меняет местами i-ю и k-ю строки матрицы А.
8.Каким образом выбирается ведущий элемент при нахождении обратной матрицы методом Гаусса–Жордана?
9.Почему при нахождении обратной матрицы необходимо запоминать номера переставляемых столбцов при выборе ведущего элемента?
2.2.4.Первый метод ортогонализации
Представим систему Ax = b в следующем виде
|
n |
|
|
|
∑Aij xj + Ain+1 = 0, i =1, n, |
(2.33) |
|
|
i=1 |
|
|
где Ain+1 = −bi . |
|
|
|
Если |
ввести (n+1)-мерные векторы Ai = (A |
,.., A , A |
), |
|
i1 |
in in+1 |
|
i =1, n; |
y = (x1,..., xn ,1) , то эти уравнения можно заменить системой |
||
скалярных произведений |
|
|
|
|
(Ai , y) = 0, i =1,n. |
(2.34) |
|
Соотношения (2.34) позволяют дать другую формулировку для
исходной задачи: в (n+1)-мерном пространстве Rn+1 найти (n+1)- мерный вектор у с уп+1 = 1, перпендикулярный п-мерной гипер-
плоскости, «натянутой» на векторы Ai , i =1,n . Если удастся по-
строить такой вектор, то первые п компонент этого вектора будут являться компонентами решения исходной системы уравнений.
44
Предлагается следующая схема решения этой задачи.
1.К исходной расширенной матрице добавляем снизу строку с
компонентами (0,0,…,1). Если матрица исходной системы невырожденная, то строки этой новой матрицы в пространстве Rn+1 образуют полную линейно-независимую систему векторов. Это следует из того, что ее определитель равен определителю исходной матрицы, который для невырожденной системы отличен от нуля.
2.Применяя к указанной полной линейно-независимой системе
векторов процедуру ортогонализации Грама–Шмидта (2.35), строим ортонормированный базис для пространства Rn+1 (рис. 2.7).
Рис. 2.7. Графическое пояснение операции процедуры Грамма–Шмидта
для k =1, n
|
|
k |
|
|
|
|
Ak |
|
|
|
k |
|
|
|
k |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
A |
|
= |
|
|
|
, |
где |
A |
|
|
|
= |
(A |
, A |
) |
|
|
|
|
Ak |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
для i = k +1, n +1 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
Ai |
= Ai −(Ai , Ak )Ak |
|
|
(2.35) |
||||||||||
|
конец i |
|
|
|
|
|
|
|
|
|
|
||||||
конец k |
An+1 |
|
|
|
|
|
|
|
|
|
|
||||||
A |
n+1 |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
An+1 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Последний орт этой системы (последняя строка расширенной матрицы) будет перпендикулярен n-мерной гиперплоскости, «натянутой» на векторы Ai , i =1, n .
Детализируем отдельные операции алгоритма процедуры ортогонализации.
n+1
1) расчет скалярного произведения sk(i, k) = (Ai , Ak ) = ∑Aij Akj
j=1
45
s = 0
для j =1, n +1
s = s + Aij Akj
конец j sk = s
2) нормировка вектора Ak = Ak
Ak
norm = sk(k, k)
если norm ≈ 0, то" матрица вырожденная", иначе norm = norm для j =1, n +1
Akj = normAkj
конец j
Нулевое значение подкоренного выражения означает линейную зависимость исходных векторов, т.е. вырожденность матрицы системы Ax=b;
3) корректировка вектора Ai = Ai −(Ai , Ak )Ak
sk _ ik = sk(i, k)
для j =1, n +1
Aij = Aij − sk _ ik Akj
конец j
3. Поделив последнюю строку матрицы на ее последнюю компоненту, получаем решение исходной системы
для k =1, n |
|
|
x = |
An+1k |
(2.36) |
|
||
k |
An+1n+1 |
|
|
|
|
конец k
Замечание. Алгоритм (2.36) необходимо поставить вместо последнего оператора в схеме (2.35), которая является общей записью алгоритма ортогонализации.
На рис. 2.8 приведены экранные формы программы (основное окно и окно справки), которая с помощью рассмотренных выше алгоритмов (пп. 2.2.2 и 2.2.4) находит решение и компоненты вектора
n
невязки ( δi = bi −∑Aij xj ) для заданной системы уравнений Ax=b.
j=1
46

Рис. 2.8. Экранные формы программы, которая находит решения произвольной системы Ax = b
47
Здесь предусмотрены возможность корректировки значения машинного нуля (переменной nul), используемого для сравнения действительных чисел с нулем, а также включение и отключение
дополнительного критерия плохо |
|
обусловленной |
матрицы |
|||||||
|
δ |
|
|
|
куб < nul (наряду с критериями |
|
Akk |
|
< nul или |
norm < nul |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||
соответственно для методов Гаусса–Жордана и ортогонализации). На рис. 2.9 и 2.10 приведены результаты использования этих дополнительных возможностей для системы уравненей с вырожденной матрицей. Сранение этих результатов наглядно показывает, к каким существенным измениниям в решении x приводит незначительная входная погрешность в правой части
системы b .
Рис. 2.9. Применение метода исключения к системе с вырожденной матрицой (ее определитель равен нулю) при nul = 1E–30. Благодаря «пропуску» ошибок округления удалось получить для данной системы одно из частных ее решений
(другое – x = (1,1,1))
48
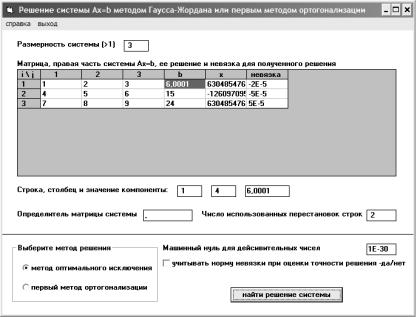
Рис. 2.10. Результат применения метода исключения к системе с вырожденной матрицей и отключенным вторым критерием по невязке. Небольшое изменение правой части системы b привело к полной перестройке решения системы x (сравните с рис. 2.9)
2.2.5. Второй метод ортогонализации
Этот метод применим к системам с симметричной положительно определенной матрицей. Поскольку только с помощью такой матрицы можно определить следующее скалярное произведение (х, Ау), удовлетворяющее всем свойствам, присущим скалярному произведению:
1)(x, Ay) = ( y, Ax) ;
2)(x + z, Ay) = (x, Ay) +(z, Ay) ;
3)(λx, Ay) = λ(x, Ay) ;
4)(x, Ax) > 0, при 
 x
x
 > 0 .
> 0 .
49

Например, проверим свойство 1, так как выполнение остальных
свойств очевидно:
(x, Ay) = ∑xi ∑Aik yk = ∑∑Aik xi yk ;
i |
k |
i |
k |
( y, Ax) = ∑yk ∑Aki xi = ∑∑Aki xi yk . |
|||
k |
i |
i |
k |
Видно, что для симметричной матрицы правые, а следовательно, и левые части этих выражений равны.
Теперь рассмотрим, как строится решение системы Ax = b данным методом.
1. Берем в пространстве Rn полную линейно-независимую cистему векторов E j , j =1, n , в виде столбцов единичной матрицы (ее определитель равен 1)
E1........En 1 0.......0
E = 0 1.......0 .
.............
00.......1
2.Применяя процедуру ортогонализации Грама–Шмидта к данной системе векторов, строим в пространстве Rn ортонормированный базис в смысле скалярного произведения (х, Ау):
для k =1, n −1
|
|
E |
k |
= |
|
|
Ek |
|
, |
где |
|
E |
k |
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
Ek |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
для j |
|
= k |
|
+1,n |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
E j = E j −(E j , AEk |
|||||||||||||||||
|
|
конец j |
|
|
|
|
|
|
|
|
|
|
|||||||||
конец k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
E |
n |
= |
|
En |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
En |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= (Ek , AEk )
)Ek
При реализации алгоритма ортогонализации все матричные операции следует заменить циклами по компонентам векторов, например:
50
E j = E j −(E j , AEk )Ek дляi =1,n {Eij = Eij −(E j , AEk )Eik }),
а перед вычислением корня, необходимо проверять, что подкоренное выражение положительное. Невыполнение этого условия означает, что матрица системы Ax = b не является положительно
определенной. |
|
|
|
Приведем алгоритм |
расчета |
скалярного произведения |
|
n |
n |
|
|
sk( j, k) ≡ (E j , AEk ) = ∑Eij ∑Aim Emk с учетом хранения векторов в |
|||
i=1 m=1 |
|
|
|
виде столбцов единичной матрицы: |
|
||
s = 0 |
|
|
|
для i =1, n |
|
||
|
buf = |
0 |
|
|
для m |
=1,n |
|
|
buf |
=buf |
+ Aim Emk |
|
конец m |
|
|
s = s + Eijbuf
конец i sk = s
3. Ищем решение системы в виде разложения по векторам построенного базиса, сформированного на месте единичной матрицы
n |
|
x = ∑cj E j |
(2.37) |
j=1 |
|
или через компоненты вектора х |
|
n |
|
xi = ∑Eijcj , i =1, n. |
(2.38) |
j=1
Для определения неизвестных коэффициентов разложения подставим разложение (2.37) в исходную систему Ax = b, а затем
умножим ее скалярно последовательно на вектора Ei , i =1, n :
n |
|
∑cj (Ei , AE j ) = (Ei ,b), i =1,n. |
(2.39) |
j=1
Ввиду ортонормированности нового базиса в левой части
уравнения (2.39) останется только одно слагаемое с j = i, равное ci. Отсюда следует, что
51

n |
|
ci = (Ei ,b) = ∑Ekibk . |
(2.40) |
k =1
Видно, что метод потребует значительного количества операций, но в методическом плане он представляет определенный интерес. По этой причине с ним полезно познакомиться.
2.2.6. Метод квадратного корня (метод Холецкого)
Метод применим только для систем с симметричной положительно определенной матрицей.
Согласно этому методу исходная матрица представляется в виде произведения двух матриц
А = ВВТ. |
(2.41) |
где В – нижняя треугольная матрица.
Такое разложение возможно только для симметричной положительно определенной матрицы:
1) AT = (BBT )T = (BT )T BT = BBT = A;
2) (Ax, x) = (BBT x, x) = (BT x, BT x) ≥ 0.
Чтобы найти рекуррентные формулы для определения компонент матрицы В, запишем матричное соотношение (2.41) для четырехмерного случая
A11 |
|
|
|
B11 |
|
|
|
B11 B21 B31 |
B41 |
|
A21 |
A22 |
A |
= |
B21 |
B22 |
B |
* |
B22 B32 |
B42 |
= |
A |
A |
|
B |
B |
|
B |
B |
|
||
31 |
32 |
33 |
|
31 |
32 |
33 |
|
33 |
43 |
|
A41 |
A42 |
A43 A44 |
|
B41 |
B42 |
B43 B44 |
|
|
B44 |
|
B112
B11B21 B212 + B222
B11B31 B31B21 + B32 B22 B312 + B322 + B332
B11B41 B41B21 + B42 B22 B41B31 + B42 B32 + B43 B33 B412 + B422 + B432 + B442
Отсюда, сравнивая компоненты левой и правой матриц, получим
52

B11 = |
A11 ; |
|
|
|
|
|
|
|
|
|
|
|
− A2 |
|
|
|
|
||||||||
|
|
|
A |
|
|
|
|
|
|
− B2 |
|
A A |
|
|
|
|
|||||||||
B |
= |
|
21 |
|
, |
B |
= |
|
|
A |
= |
|
11 22 |
|
21 |
|
; |
|
|
|
|||||
|
|
|
|
|
A11 |
|
|
|
|
||||||||||||||||
21 |
|
|
B11 |
22 |
|
|
|
|
22 |
21 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
A |
|
|
|
A |
|
− B B |
|
|
|
|
|
|
|
|
|
|
|
|||||
B |
= |
|
31 |
, |
B |
= |
32 |
|
31 21 |
, |
B = |
A |
− B2 |
− B2 |
; |
|
|||||||||
|
|
|
|
|
|
||||||||||||||||||||
31 |
|
|
B11 |
32 |
|
|
|
|
B22 |
|
|
|
|
33 |
|
33 |
|
|
31 |
32 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
A43 − B41B31 − B42 B32 |
|
|||||||||||
B = |
A41 |
, |
B = |
|
A42 − B41B21 |
, |
B = |
, |
|||||||||||||||||
|
|
|
|||||||||||||||||||||||
41 |
|
|
B11 |
42 |
|
|
|
|
B22 |
|
|
|
|
43 |
|
|
|
|
B33 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
B = A − B2 |
− B2 |
− B2 . |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
44 |
|
|
|
|
44 |
41 |
|
|
|
42 |
43 |
|
|
|
|
|
|
|
|
Здесь в двух верхних строчках под корнем явно присутствуют определители первых миноров исходной матрицы, а согласно критерию Сильвестра для положительно определенной матрицы они положительны. Последнее утверждение справедливо и для остальных подкоренных выражений. Это еще раз подтверждает необходимость того, чтобы матрица была положительно определенной.
Эти формулы по индукции позволяют записать следующий алгоритм расчета всех компонент матрицы В для п-мерного случая
B11 = A11 ; |
|
|
|
|
|
|
|
|
|
||||
B = |
A21 |
|
, |
B = A − B2 |
; |
||||||||
|
|
||||||||||||
21 |
|
B11 |
|
|
|
22 |
22 |
21 |
|
||||
|
|
для k = 3, n |
|
|
|
||||||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
{ |
Ak1 |
|
|
|
|
||
|
|
|
|
B |
|
= |
; |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
k1 |
|
|
|
B11 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
для i = 2, k −1 |
|
|
(2.42) |
||||||||
|
|
|
|
|
|
{ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i−1 |
|
|
|
|
|
|
|
|
|
|
Aki −∑Bkj Bij |
|
|
|
|||
|
|
Bki |
= |
|
|
|
j=1 |
|
|
|
|||
|
|
|
|
|
Bii |
|
|
|
|||||
|
|
|
|
|
|
} |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
k −1 |
|
|
|
|
|
Bkk |
= |
|
Akk |
−∑Bkj2 |
|
|
|
|||||
j=1
}
53
При программной реализации этого алгоритма перед вычислением корня необходимо предварительно проверять является ли подкоренное выражение положительным. Если это условие не выполняется, то исходная матрица не положительно определенная. Отметим, что этот алгоритм можно использовать для проверки положительной определенности произвольной симметричной матрицы.
После того как разложение матрицы A выполнено, система Ax = b распадается на две системы с треугольными матрицами
Ax = b BBT x = b By = b,
|
|
|
|
|
BT x = y |
|
|||||||||
или в покомпонентной записи |
|
|
|
|
|
|
|
|
|
|
|
||||
|
B11 y1 |
+ B22 y2 |
|
|
|
|
|
|
=b1 |
||||||
|
B21 y1 |
|
|
|
|
|
|
= b2 |
|||||||
|
.................... |
|
|
|
|
|
|
|
|
|
|||||
|
Bi1 y1 |
+ Bi |
2 y2 +... |
+ Bii yi |
= bi |
||||||||||
|
..................... |
|
|
|
|
|
|
|
|
||||||
|
................. |
|
|
|
|
|
|
|
|
|
|
||||
|
Bii xi + Bi+1i xi+1 |
+.... + Bni xn = yi |
|||||||||||||
|
................... |
|
|
|
|
|
|
|
|
|
|
||||
|
|
Bn−1n−1xn−1 + Bnn−1xn = yn−1 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Bnn xn |
= yn |
||
Их решение рассчитывается элементарно |
|
||||||||||||||
|
|
|
|
y = |
b1 |
; |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
1 |
|
B11 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
i−1 |
|
|
|
|
|
|
|
||
|
|
|
bi |
−∑Bij y j |
|
||||||||||
для i = 2, п |
{ yi = |
|
|
|
j=1 |
|
|
|
|
}; |
|
||||
|
|
|
Bii |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
x |
= |
yn |
|
; |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
n |
|
|
|
Bnn |
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
yi − ∑ Bji xj |
|
||||||||||
для i = (n – 1), 1 |
{ xi |
= |
|
|
|
j=i |
+1 |
|
|
|
}. |
|
|||
|
|
|
|
Bii |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
54
Последовательное вычисление компонент промежуточного вектора y можно выполнять в алгоритме (2.42) после определения компонент соответствующей строки матрицы B (см. приведенный ранее алгоритм). При этом для экономии памяти матрицу B можно хранить на месте исходной матрицы A, а вектор y формировать на месте вектора x.
Необходимо помнить, что все суммы, встречающиеся в алгоритмах, вычисляется путем введения соответствующих внутренних циклов.
В заключение привем листинг на Visual Basic процедурыфункции, реализующей метод квадратного корня с использованием приведенных алгоритмов:
Function kvroot () As Integer Dim i%, j%, k%
kvroot = 0 'матрица положительно-определенная
If Not (a(0, 0) > 0) Then
kvroot = 1 'матрица не положительноопределенная
Exit Function End If
a(0, 0) = Sqr(a(0, 0)) x(0) = a(0, n) / a(0, 0) a(1, 0) = a(1, 0) / a(0, 0) x(1) = a(1, n)
a(1, 1) = a(1, 1) - a(1, 0) * a(1, 0) If Not (a(1, 1) > 0) Then
kvroot = 1 'матрица не положительноопределенная
Exit Function End If
a(1, 1) = Sqr(a(1, 1))
x(1) = (x(1) - a(1, 0) * x(0)) / a(1, 1) If n = 2 Then GoTo cont
For k = 2 To n - 1
a(k, 0) = a(k, 0) / a(0, 0) x(k) = a(k, n) - a(k, 0) * x(0) For i = 1 To k - 1
For j = 0 To i - 1
55
a(k, i) = a(k, i) - a(k, j) * a(i, j) Next j
a(k, i) = a(k, i) / a(i, i) x(k) = x(k) - a(k, i) * x(i)
Next i
For j = 0 To k - 1
a(k, k) = a(k, k) - a(k, j) * a(k, j) Next j
If Not (a(k, k) > 0) Then
kvroot = 1 'матрица не положительноопределенная
Exit Function End If
a(k, k) = Sqr(a(k, k)) x(k) = x(k) / a(k, k)
Next k cont:
x(n - 1) = x(n - 1) / a(n - 1, n - 1) For i = n - 2 To 0 Step -1
For j = i + 1 To n - 1 x(i) = x(i) - a(j, i) * x(j)
Next j
x(i) = x(i) / a(i, i) Next i
End Function
Здесь систама хранится в расширенной матрице с
компонентами: a(0,0),…a(n-1,n).
На рис. 2.11 представлен скриншот программы, которая позволяет найти решение проивольной системы линейных уравнений как вторым методом ортогонализации, так и методом квадратного корня. Для преобразования произвольной системы в равносильную систему с симметричной и положительно определенной матрицей следует использовать кнопку «Умножить систему на А(т)» – умножить систему на транспонированную исходную матрицу. Есть возможность задать систему уравнений случайным образом. Это позволяет провести сравнительный анализ точности (по норме невязки полученного решения) используемых методов.
56
Рис. 2.11. Экранная форма программы, которая реализуют два метода, используемые для положительно определенной симметричной матрицы.
2.2.7. Метод прогонки
Метод прогонки является самым экономичным способом решения систем с трех диагональной матрицей
b1x1 + c1x2 = d1;
................ |
|
ak xk −1 +bk xk + ck xk +1 = dk , k = 2, n −1; |
(2.43) |
................. |
|
an xn−1 +bn xn = dn .
Здесь для хранения системы использованы четыре вектора a, b, c, d, причем компоненты a1 = cn = 0 не используются.
К таким системам сводится разностное решение краевых задач
для дифференциальных уравнений второго порядка. |
|
Введем рекуррентные зависимости |
|
xk =αk xk +1 +βk , k =1, n −1. |
(2.44) |
|
57 |

Найдем формулы для расчета входящих в (2.44) неизвестных параметров αk, βk. Сравнивая первое уравнение в (2.43) с
соотношением (2.44), сразу получаем |
|
|
|
|||
α = − |
c1 |
, |
β = |
d1 |
. |
(2.45) |
|
|
|||||
1 |
b1 |
|
1 |
b1 |
|
|
|
|
|
|
|||
Далее, заменим в k-ом уравнении системы (2.43) неизвестное xk–1 согласно формуле (2.44)
ak (αk −1xk +βk −1 ) +bk xk + ck xk +1 = dk .
Отсюда легко выводим рекуррентные формулы для последовательного определения остальных неизвестных параметров αk, βk :
αk = − |
ck |
, βk = |
dk −akβk −1 |
, |
k = 2,n −1, |
tk |
|
||||
|
|
tk |
(2.46) |
||
tk = bk + ak αk −1 .
Вычисления по формулам (2.45), (2.46) называется прямым ходом прогонки.
Теперь, подставляя в последнее уравнение (2.43) соотношение
(2.44) с k = n – 1, получим |
|
|
|
dn − anβn−1 |
|
|
||||||
a |
(α |
x |
+β |
n−1 |
) +b x |
= d |
k |
x = |
. |
(2.47) |
||
|
||||||||||||
n |
|
n−1 n |
|
n n |
|
n |
bn + anαn−1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|||
Формулы (2.47) и (2.44) (с k = n –1, n – 2,...,1) позволяют рассчитать все компоненты xk неизвестного решения системы (2.43). Эти расчеты называются обратным ходом прогонки.
Покажем методом индукции, что для устойчивости метода прогонки ( bk + ak αk −1 > 0 ) достаточно выполнения следующих соотношений между параметрами системы
|
|
|
|
|
|
|
|
|
bk |
|
≥ |
|
ak |
|
+ |
|
ck |
|
> 0 |
при k . |
|
|
|
|
(2.48) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
При выполнении условия |
(2.48) имеем (см. |
(2.45)) |
|
b1 |
|
> 0 |
|||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||
и |
|
α1 |
|
<1. Предположим, что |
|
|
|
αk −1 |
|
<1. |
Тогда |
|
|
|
bk |
+ ak αk −1 |
|
|
> 0 . |
||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
Кроме того, |
|
bk + ak αk −1 |
|
> |
|
ck |
|
и, следовательно, |
|
αk |
|
<1 |
и т.д. |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Заметим, что метод прогонки легко обобщается на системы с пяти (и более) диагональными матрицами. В этом случае исходное рекуррентное соотношение следует брать в виде
58
xk =αk xk +1 +βk xk +2 + γk .
Замечание. При программной реализации метода, в целях экономии памяти, параметры αk , βk можно сохранять на месте
компонент векторов bk , dk , а решение вернуть в векторе с. В этом случае алгоритм метода будет иметь вид
прямой ходпрогонки |
||||||||||
d |
= |
d1 |
, b |
= − |
c1 |
|
|
|||
|
|
|
||||||||
1 |
|
b1 |
1 |
|
|
b1 |
||||
|
|
|
|
|
||||||
для k = 2, (n −1) |
||||||||||
{ |
t = bk + ak bk −1 |
|||||||||
|
d = |
dk + ak dk −1 |
|
|||||||
|
|
t |
||||||||
|
b = − |
c |
|
|||||||
|
k |
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||
|
k |
t |
|
|
|
|
|
|||
} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
обратный ходпрогонки |
|||
с |
= dn −andn−1 |
||
n |
bn + anbn−1 |
|
|
|
|
||
для k = (n −1),1 |
|||
{ |
ck = bk ck +1 + dk |
||
}
2.3Метод регуляризации для решения плохо обусловленных систем
Решение системы уравнений Ax = b с плохо обусловленной матрицей существенно зависит от ошибок в исходных данных и ошибок округления (рис. 2.12, где для таких систем схематично показаны соответствующие области входных и выходных ошибок).
Согласно методу регуляризации для уменьшения этой зависимости, т.е. сужения области поиска, на решение системы накладывается дополнительное вполне разумное требование, чтобы его норма наименее уклонялось от нуля. В такой постановке
59

исходную систему можно свести к задаче минимизации следующего квадратичного функционала
min F(x) = (Ax −b, Ax −b) + α(x, x) ≥ 0, |
(2.49) |
x |
|
где α > 0 – весовой коэффициент, называемый параметром регуляризации. Его значение должен быть таким, чтобы с одной стороны обеспечить достаточную обусловленность системы, а с другой – хорошую аппроксимацию исходной задачи.
Рис. 2.12. Области входных и выходных ошибок
Для квадратичного функционала (2.49) решение, обеспечивающее минимум функционалу, находится аналитически из условия
dFdx = 0 . Для этого распишем (2.49) в виде
F(x) = (x, AT Ax) − 2(x, AT b) +(b,b) +α(x, x). |
(2.50) |
|||
Отсюда, беря производную |
dF |
с учетом очевидного преоб- |
||
dx |
||||
|
|
|
||
разования (x, AT Ax) = ( AT Ax, x) = (x,(AT A)T x) = (x, AT Ax) |
и прирав- |
|||
нивая ее нулю, получим новую систему уравнений |
|
|||
(AT A +αE)x = AT b. |
(2.51) |
|||
Ее решение хα, называемое нормальным, зависит от α и может быть получено любым рассмотренным ранее методом.
В заключение укажем способ выбора параметра α. Обычно на практике проводится ряд вычислений с различными значениями α. После этого оптимальным считают либо то его значение, при
60
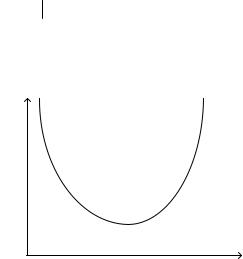
котором выполняется условие приближенного равенства невязки решения сумме погрешностей исходных данных
|
δ(xα ) |
|
|
|
≡ |
|
|
|
Axα −b |
|
|
|
≈ |
|
|
|
δb |
|
|
|
+ |
|
|
|
δA xα |
|
|
|
, |
(2.52) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
либо то из них, для которого невязка минимальна (рис. 2.13). Соответствующее этому α решение хα принимается за нормаль-
ное решение исходной системы.
Рис. 2.13. Зависимость навязки δ от параметра α, где в зоне 1 преобладает ошибка, связанная с особенностью матрицы системы, а в зоне 2 – ошибки аппроксимации, связанные с изменением исходной системы
1 преобладает ошибка, связанная с особенностью матрицы системы, а в зоне 2 – ошибки аппроксимации, связанные с изменением исходной системы
На рис. 2.14 и 2.15 приведены результаты работы программы, позволяющей использовать метод регуляризации для нахождения решения систем уравнений с плохо обусловленными матрицами.
Вопросы и задания для самоконтроля
1. При каком условии вектор y = (x1 ,..., xn ,1) , используемый в первом
методе ортогонализации, будет линейно-независимым от векторов-строк расширенной матрицы А?
2.Какие манипуляции с векторами выполняет процедура Грамма– Шмидта?
3.Как с помощью процедуры Грамма–Шмидта можно проверить: является ли система векторов линейно независимой?
4.Для каких систем линейных уравнений можно использовать второй метод ортогонализации и почему?
61
Рис. 2.14. Получено нормальное решение системы с плохо обусловленной матрицей. Заметим, что точное решение исходной системы равно (1; 1; 1). Видно, что решить непосредственно исходную систему методом Гаусса-Жордано не
удалось.
Рис. 2.15. Норма невязки исходной системы для нормального решения
62
5.В чем сущность метода квадратного корня и почему он применяется только для систем с симметричной положительно определенной матрицей?
6.Запишите алгоритм модифицированного метода ортогонализации Грамма–Шмидта.
7.Как подбирается параметр α в методе регуляризации, используемом при решении плохо обусловленных систем линейных уравнений?
8.Запишите условие сходимости метода прогонки.
9.Составьте алгоритм метода прогонки.
10.Распишите через компоненты скалярное произведение двух
столбцов единичной матрицы sk( j, k) ≡ (E j , AEk ) и составьте алгоритм для вычисления его значения.
63
Глава 3. МЕТОДЫ РЕШЕНИЯ ЗАДАЧИ НА СОБСТВЕННЫЕ ЗНАЧЕНИЯ
3.1.Собственные значения и собственные векторы матрицы
Собственным числом (значением) матрицы называется действительное или комплексное число λ, которое удовлетворяет системе
Ax = λx (Ax −λE)x = 0. |
(3.1) |
При этом нетривиальный вектор х является собственным вектором, соответствующим данному λ.
Для того чтобы система (3.1) имела нетривиальное решение,
должно выполнятся равенство |
|
det(Ax −λE) = 0. |
(3.2) |
Уравнение (3.2), называемое характеристическим полиномом
матрицы А, представляет собой полином степени п относительно λ и имеет п корней. Приведем некоторые свойства собственных значений и векторов.
1.Матрица А порядка п×п имеет п собственных значений.
2.Для каждого уникального λ существует, по крайней мере, один собственный вектор (так как не всегда k-кратное собственное число имеет k собственных векторов). Каждый собственный вектор
определяет для данной матрицы только собственное направление в пространстве Rn.
3.Собственные векторы, соответствующие различным λ, линейно-независимы.
Доказательство этого утверждения проведем «по принципу индукции».
Имеем a1x1 = 0 a1 = 0 .
k
Пусть ∑ai xi = 0 при ai = 0, i =1,k, т.е. векторы х1, ..., хk –
i=1
линейно-независимы.
Докажем, что векторы х1, ..., хk, xk+1 – также линейнонезависимые. Доказательство проведем «от противного». Предположим, что это не так, т.е. что
64
k +1 |
|
∑ai xi = 0 |
(3.3) |
i=1
ине все ai = 0. Умножим равенство (3.3) на матричный оператор
(A −λk +1E) :
k +1 |
k +1 |
k +1 |
k +1 |
|
(A −λk +1E)∑ai xi = ∑Aai xi −∑λk +1ai xi = ∑(λi −λk +1 )ai xi = |
|
|||
i=1 |
i=1 |
i=1 |
i=1 |
(3.4) |
|
|
|
|
|
k
= ∑(λi −λk +1 )ai xi = 0.
i=1
Но по предположению вектора х1, ..., хk – линейно-независимые,
и поэтому |
|
|
|
|
(λi −λk +1 )ai = 0 |
ai = 0, |
|
так как |
(λi −λk +1 ) ≠ 0 для i =1,k . Отсюда согласно равенству (3.3) |
||
ak +1 = 0 |
и, следовательно, в (3.3) |
все |
ai = 0, i =1, k +1 . А это |
означает, что все векторы х1, ..., хk, xk+1 – |
линейно-независимые. |
||
4.Если все собственные числа матрицы простые, то
соответствующие им собственные вектора образуют полную линейно-независимую систему векторов в пространстве Rn, так что любой вектор из этого пространства может быть представлен в виде линейной комбинации этих векторов.
5.Собственные числа действительной, симметричной матрицы являются действительными числами. Кроме того, если матрица положительно определенная, то ее собственные числа положительные. Пусть x – собственный вектор матрицы A. Тогда
(Ax, x) = λ(x, x). |
(3.5) |
Отсюда, так как (Ах, х) для симметричной матрицы и (х, х) действительные числа, следует, что λ – также действительное. Если матрица положительно определенная, то в (3.5) (Ax, x) > 0 ,
(x, x) > 0, и поэтому λ > 0 .
6. Симметричная, действительная матрица всегда имеет полную ортонормированную систему собственных векторов, которую можно использовать как базис для пространства Rn.
k
7. Матрицы А, А–1 и B = ∑ci Ai имеют одни и те же собственные
i=1
векторы, а собственные числа двух последних матриц λ(A−1 ), λ(B)
65

связаны с собственными числами матрицы А ( λ(A) ) соотноше-
ниями:
Ax = λ(A)x x = λ(A) A−1x A−1x =
1 |
x λ( A−1 ) = |
1 |
; |
||
|
λ( A) |
|
λ(A) |
||
|
x = λ(B)x |
|
|
||
Bx = λ(B)x ∑ci Ai |
∑ciλ(A)i x = λ(B)x (3.6) |
||||
k |
|
|
k |
|
|
i=1 |
|
|
i=1 |
|
|
k
λ(B) = ∑ci λ(A)i .
i=1
8.Преобразование матрицы А вида С = В–1АВ, где матрица В – невырожденная ( det(B) ≠ 0 ), называется подобным, а сами матри-
цы А и С подобными. Подобные матрицы имеют одинаковые характеристические полиномы, так как
det(C −λE) = det(B−1 AB −λE) = det(B−1 AB −λB−1EB) = = det(B−1 )det(A −λE)det(B) = det(A −λE)
учтено, что det(B−1 ) = det(1B) , и, следовательно, одинаковые
собственные числа, а их собственные векторы (соответственно х и у) связаны соотношением
Cy = λy B−1 ABy = λy A(By) = λ(By) x = By.
Если В–1 = ВТ, то преобразование, выполняемое над А с помощью такой матрицы, называется ортогональным подобным преобразованием.
9. Для любой нормы матрицы справедливо неравенство λi ≤ 
 A
A
 . Оно следует из цепочки соотношений:
. Оно следует из цепочки соотношений:
Ax = λx 
 A
A


 x
x
 ≥
≥ 
 Ax
Ax
 =
= 
 λx
λx
 = λ
= λ

 x
x
 .
.
В заключение приведем два полезных соотношения, которые на практике могут быть использованы для нахождения двух последних неизвестных собственных значений или проверки
надежности рассчитанной совокупности собственных значений:
n
det(A) =λ1...λn ; trace(A) ≡ ∑Aii = λ1 +... + λn .
i=1
66
Подумайте: будут ли эти соотношения выполняться для действительной матрицы при наличии у нее комплексных собственных значений?
3.2. Решение частичной проблемы собственных чисел для симметричной матрицы
Рассмотрим итерационный метод нахождения максимального по модулю собственного числа симметричной матрицы. Все собственные числа такой матрицы действительные, а собственные вектора ei, i = 1, n, образуют в пространстве Rn ортонормированный базис.
Замечание. Этот метод применим и для обычной матрицы, если у нее существует полный набор собственных векторов и собственные числа действительные. В этом случае может пригодиться теорема Пиррона: если все компоненты матрицы положительные ( Aij > 0 ), то максимальное собственное число
матрицы простое и положительное λ1 > 0 . |
|
|
|
|
|
|||||||||
Случай 1. Пусть λ1 = λ2 =... = λr |
и |
|
λ1 |
|
> |
|
λr +1 |
|
>... > |
|
λn |
|
. Возьмем |
|
|
|
|
|
|
|
|||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
произвольный вектор x(0) = ∑ciei |
|
и |
|
будем |
последовательно |
|||||||||
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
умножать его на матрицу А: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
x(k ) = Ax(k −1) |
= ∑ciλik ei . |
(3.7) |
||||||||||||
i=1
Для полученных таким образом векторов можно построить скалярные произведения (учтено, что векторы ei , i =1,n, ортонормированны)
n |
n |
|
n |
(x(k −1) , x(k −1) ) = ∑∑cicj λik −1λkj −1 (ei ,ej ) = ∑ci2λi2k −2 = |
|||
i=1 j=1 |
|
i=1 |
|
= λ2k −2 (c + c |
+... + c +O(γ2k −2 )); |
||
1 |
1 2 |
r |
|
|
n |
n |
|
(x(k ) , x(k −1) ) = ∑∑ci cj λik λkj |
−1 (ei ,ej ) = |
||
|
i=1 |
j=1 |
|
67
|
|
n |
|
|
|
= ∑ci2λi2k −1 = λ12k −1 (c1 +c2 +... +cr +O(γ2k −1 )), |
(3.8) |
|
|
i=1 |
|
где γ = |
λr +1 |
<1 . |
|
λ |
|
||
|
|
|
|
|
1 |
|
|
Отношение этих скалярных произведений при k → ∞ стремится к максимальному по модулю собственному числу матрицы A:
(x(k ) , x(k −1) ) |
=λ +O(γ2k −2 ) ≈ λ . |
(3.9) |
||
(x(k −1) , x(k −1) ) |
||||
1 |
1 |
|
||
При этом один из собственных векторов, соответствующих данному кратному собственному числу (поскольку любая линейная комбинация этих собственных векторов также является собст-
r |
r |
венным вектором A(∑ciei ) = λ1 (∑ciei ) , т.е. эти векторы определя- |
|
i=1 |
i=1 |
ют r-мерную собственную гиперплоскость для λ1), определяется выражением
|
|
|
|
|
n |
|
|
|
|
|
|
|
x(k ) |
|
= |
∑ciλik ei |
= |
λk (c e +c e |
+... + c e +O(γk )) |
= |
|||
|
|
|
|
i=1 |
|
|
1 1 1 2 2 |
r r |
|||
|
x(k ) |
|
|
|
|
|
|||||
|
|
|
|
n |
2 |
2k |
|
λ12k (c12 +c22 +... +cr2 +O(γ2k )) |
(3.10) |
||
|
|
|
|
|
∑ci |
λi |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
i=1
= e1 +O(γk ) ≈ e1.
Чтобы для λ1 найти остальные собственные векторы, необходимо повторить описанную итерационную процедуру, но с другими начальными векторами.
В заключение приведем модифицированный вариант итерационной процедуры, который позволяет избежать возможных аварийных ситуаций, связанных с переполнением (когда λ1 >1 )
или «исчезновением порядка» (когда λ1 <1):
e |
(0) |
= |
|
x(0) |
, где |
|
x |
(0) |
|
|
|
= (x |
(0) |
, x |
(0) |
); |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
1 |
|
|
x(0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
λ(0) |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1030 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
|
|
- максимальноечислоитераций; |
||||||||||
для k =1, Kmax |
||||||||||||||||
68

|
x |
(k ) |
= |
Ae |
(k −1) |
, |
λ |
(k ) |
= (x |
(k ) |
,e |
(k |
−1) |
), e |
(k −1) |
= |
|
x(k ) |
|
||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
x(k ) |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
если |
|
λ1(k ) |
−λ1(k -1) |
|
< eps, товыходизцикла |
(3.11) |
||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
|
иначе |
λ(k −1) |
= λ(k ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
конец цикла по k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Такая запись справедлива, так как |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
(x(k ) , x(k −1) ) |
|
= |
( |
Ax(k −1) , x(k −1) ) |
= (Ae(k −1) ,e(k −1) ) |
|
||||||||||||||||||||||
|
(x(k −1) , x(k −1) ) |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
x(k −1) |
|
x(k −1) |
|
|
|
|
|
|
|
|
|
|
|||||||||||
Случай 2 не возможен для положительно определенной матри-
цы, так как у нее все λi |
> 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Пусть λ1 = −λ2 |
и |
|
|
λ1 |
|
= |
|
|
|
λ2 |
|
|
|
> |
|
λ3 |
|
... > |
|
λn |
|
. Тогда |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
s1 ≡ |
|
(x(k ) , x(k −1) ) |
|
|
|
= |
|
|
|
λ2k −1 |
(c2 |
−c2 |
+O(γ2k −1 )) |
|
→ |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
2 |
|
|
|
|
|
|
|
||||||||||
(x(k |
−1) , x(k −1) ) |
|
|
|
λ2k −2 |
(c2 |
+ c2 |
+O(γ2k − |
2 )) |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
c2 |
−c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
→ λ |
( |
|
|
|
|
1 |
|
|
|
2 |
) +O(γ2k −2 ); |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
+ c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
s2 ≡ |
(x(k ) , x(k ) ) |
|
|
|
|
= |
|
|
|
λ2k (c2 |
+c2 |
+O(γ2k −1 )) |
|
→ |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
2 |
|
|
|
|
|
|
(3.12) |
||||||||||||||
(x(k −1) , x(k −1) ) |
|
|
λ2k −2 |
(c2 |
+c2 |
+O(γ2k −2 )) |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
→ λ2 +O(γ2k −2 ); |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
e(k ) ≡ |
|
x(k ) |
|
|
= |
λk |
(c e + (−1)k c e +O(γk )) |
→ |
|
|||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
1 1 |
|
|
|
|
|
|
2 2 |
|
|
|
|||||||||||||||||||
|
x(k ) |
|
|
|
|
|
|
|
λ12k (c12 +c22 +O(γ2k )) |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
→ a(c1e1 +(−1)k c2e2 ) +O(γk ),
где а = const.
Видно, что в этом случае при k → ∞ (s1 )2 ≠ s2 , и вектор е(k)
поочередно меняет свое «значение». Оба собственных вектора е1 и е2 можно определить из соотношений (здесь k – четное):
e(k ) = ac1e1 + ac2e2 ; e(k −1) = ac1e1 − ac2e2 .
следующим образом (так как собственные вектора определяются с точность до константы)
69
e |
≡ 2ac e = e(k ) + e(k −1) |
; |
|
||
1 |
1 |
1 |
|
(3.13) |
|
e |
≡ 2ac e = e(k ) −e(k −1) . |
||||
|
|||||
2 |
2 |
2 |
|
|
|
Ниже представлен обобщенный модифицированный алгоритм нахождения максимального по модулю собственного числа, учитывающий возможность появления любого из случаев
e(0) = |
|
|
|
x(0) |
, где |
|
|
|
x(0) |
|
= |
(x(0) , x(0) ) |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
1 |
|
|
|
|
|
|
x(0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
(0) |
|
2 |
|
|
30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
) |
|
=10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
(λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
|
|
|
=1, K max |
|
- максимальное числоитераций |
||||||||||||||||||||||||
для k |
|
|
||||||||||||||||||||||||||||
|
x(k ) = Ae(k −1) , λ(k ) |
= (x(k ) ,e(k −1) ) |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
x(k ) |
||
|
|
(k ) |
|
2 |
|
|
|
x |
(k ) |
|
|
|
2 |
|
= (x |
(k ) |
, x |
(k ) |
), e |
(k −1) |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
(λ |
|
|
|
) |
|
≡ |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
x(k ) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
если (λ1(k) )2 −(λ1(k-1) )2 < eps, товыходизцикла
иначе (λ1(k −1) )2 = (λ1(k ) )2
конец цикла по к
если (λ1(k ) )2 −(λ1(k ) )2 = 0,0001, тоλ1 = λ1(k ) − имеет местослучай1 иначеλ1 = (λ1(k ) )2 − имеет местослучай 2
(3.14)
Посмотрим, какую информацию относительно собственных значений матрицы А можно получить, если применить процедуру (3.14) к симметричным матрицам вида:
|
|
|
|
|
|
n |
|
|
|
B = E − |
A |
2 |
( B = δ |
|
− |
∑Aim Amj |
, i, j =1,n ) |
и C =λ E − A . |
|
|
ij |
m=1 |
|||||||
λ2 |
λ2 |
||||||||
|
ij |
|
|
1 |
|||||
|
1 |
|
|
1 |
|
|
|||
Принадлежность собственных значений матрицам будем обозначать следующим образом: λi (A), λi (B), λi (C) .
1. Определение минимального по модулю собственного числа
матрицы А. Его можно рассчитать как |
|
|
|
|
|
|
|
|
|
||||||||
λ |
(B) =1− |
λ2 |
(A) |
|
|
λ |
|
(A) |
|
= |
|
λ |
(A) |
|
1 |
−λ |
(B) . |
n |
|
|
n |
|
|
|
|||||||||||
1 |
|
λ2 |
(A) |
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Или если матрица А положительно определенная (А > 0), то матрица С ≥ 0, и поэтому
70
λ1 (C) = λ1 (A) −λn (A) > 0 λn (A) = λ1 (A) −λ1 (C) .
2. Определение границ отрезка, содержащего все собственные значения матрицы А.
-Если при реализации процедуры (3.14) имеет место случай 2 ( λ1 = −λ2 ), то
λmin (A) = −λ1 (A), λmax (A) = λ1 (A).
-Если матрица А положительно определенная, то
λmin (A) = λn (A) = λ1 (A) −λ1 (C) > 0,
λmax (A) = λ1 (A) > 0.
-Если λ1 (C) > 0, λ1 (A) > 0 , то
λmin (A) = λ1 (A) −λ1 (C) < 0,
λmax (A) = λ1 (A) > 0.
-Если λ1 (A) < 0, λ1 (C) < 0 , то
λmin (A) = λ1 ( A) < 0,
λmax (A) = λ1 (A) −λ1 (C) < 0 или > 0.
На рис. 3.1 и 3.2 приведены скриншоты программы, в которой использован алгоритм (3.14). Программа позволяет задать «в ручную» или случайным образом произвольную исходную матрицу А, найти для нее максимальное по модулю собственное число, с помощью этих данных сформировать два варианта вспомогательной матрицы В и определить для нее максимальное по модулю собственное число. Используя эту информацию, пользователь может рассчитать минимальное по модулю собственное число матрицы А и границы отрезка, содержащего все ее собственные значения. Например, согласно результатам, представленным на рис. 3.1 и 3.2, следует, что все собственные числа использованной матрицы лежат на отрезке
λmin (A) = λ1 (A) = −0,83092;
λmax (A) = λ1 (A) −λ1 (B) = −0,83092 −(−1,41574) = 0,58482.
Втабл. 3.1 приведены результаты небольшого исследования, выполненного с помощью указанной программы. Строгая регулярность в представленных результатах отсутствует.
71

72
Рис. 3.1. Задана случайным образом симметричная исходная матрица А и найдено ее максимальное по модулю собственное число
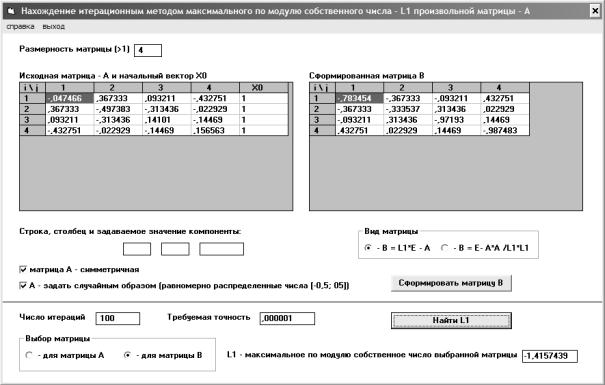
73
Рис. 3.2. Для исходной матрицы сформирована вспомогательная матрица В и найдено ее максимальное по модулю собственное число

Таблица 3.1
Зависимость числа итераций
от размерности случайной матрицы для esp = 0,000001. Величина выборки –5
Размерность A |
5 |
10 |
15 |
20 |
|
|
|
|
|
Минимум итераций |
17 |
26 |
49 |
27 |
|
|
|
|
|
Максимум итераций |
44 |
96 |
196 |
123 |
|
|
|
|
|
Вопросы и задания для самоконтроля
x(k )
1. Для чего производят нормировку текущего вектора e1(k ) = x(k )
при реализации итерационного метода нахождения максимального собственного значения?
2.Что такое характеристический полином матрицы?
3.Почему рассмотренный итерационный метод нахождения максимального по модулю собственного значения не всегда можно применить для произвольной матрицы?
4.Как с помощью рассмотренного итерационного метода найти минимальное по модулю собственное значение матрицы?
5.Как связаны между собой собственные значения и собственные
k
вектора следующих матриц А и B = ∑Ai ?
i=0
6. Составьте алгоритмы для вычисления компонент матриц
B = E − A2 и C =λ1E − A .
λ12
7.Какие матрицы называются подобными?
8.Чем можно объяснить отсутствие строгой регулярности в результатах, представленных в таблице 3.1?
74
3.3.Решение задачи на собственные значения методом Данилевского
Сущность метода Данилевского состоит в приведении матрицы А с помощью (п – 1) подобных преобразований к подобной ей матрице Фробениуса
p |
p |
p ...p |
|
p |
|
|
||
|
1 |
2 |
3 |
|
n−1 |
n |
|
|
1 |
|
0 |
0 ...0 |
0 |
|
|
||
P = 0 |
|
1 |
0 |
...0 |
0 |
. |
(3.15) |
|
|
|
|
|
|
|
|
|
|
............................ |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
...1 |
0 |
|
|
|
0 |
|
|
|
|||||
Для последней характеристический полином записывается просто путем разложения по элементам первой строки
|
p −λ p |
p ... p |
n−1 |
p |
n |
|
|
|
||
|
|
1 |
2 |
3 |
|
|
|
|
||
|
1 |
|
−λ |
0 ... 0 |
0 |
|
|
|
||
det(P −λE) = 0 |
|
1 −λ ... 0 |
0 |
|
= |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
............................ |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 ... 1 −λ |
|
|
|
|||
|
0 |
|
|
|
|
|||||
= ( p −λ)(−λ)n−1 |
− p |
(−λ)n−2 |
+... +(−1)n+1 p |
(3.16) |
||||||
1 |
|
2 |
|
|
|
|
|
n |
|
|
λn − p1λn−1 − p2λn−2 −... − pn = 0.
Подобное преобразование матрицы А представляет собой последовательный перевод ее строк, начиная с п-й, в строки матрицы Фробениуса. Детально рассмотрим k-е ( k =1,2,...(n −1) ) преоб-
разование, формирующее (п – (k – 1))-ю строку матрицы Р. После (k – 1)-го преобразования матрица имеет вид (А(0) = А):
|
(k −1) |
(k −1) |
(k −1) |
(k −1) |
(k −1) |
|
|
A11 ...... |
A1n−k |
A1n−(k +1) ......... |
A1n _1 |
A1n |
|
|
|
.......................................................................... |
|
|
|
|
|
|
|
|
(k −1) |
(k −1) |
(k −1) |
(k −1) |
(k −1) |
|
(3.17) |
A(k −1) = An−(k −1)1 |
... An−(k −1)n−k An−(k −1)n−(k +1) |
... An−(k −1)n−1 An−(k −1)n . |
|||||
0.............. |
|
0 |
1 ..................... |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
.......................................................................... |
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
0 |
|
|
0 ............. |
|
|
|
||||
75

Над ней выполняются следующие операции: 1) «сажаем» единицу на место компоненты
деления на нее всего (n – k)-го столбца
(k ) |
A(k −1) |
|
in−k |
|
|
Ain−k = |
|
, i =1,n −(k −1); |
A(k −1) |
||
|
n−(k −1)n−k |
|
A(k −1) |
путем |
n−(k −1)n−k |
|
(3.18)
2) oбнуляем все остальные компоненты приводимой строки. Для этого вычитаем из каждого j-го столбца (n – k)-й столбец, умно-
женный на соответствующую компоненту |
A(k −1) |
||
|
|
|
n−(k −1) j |
строки |
|
(k ) (k −1) |
|
(k ) |
(k −1) |
|
|
Aij |
= Aij |
− Ai n−k An−(k −1) j , |
|
i =1, n −(k −1), j =1, n ( j ≠ n −k).
(п – (k – 1))-й
(3.19)
Эти операции равносильны матричной операции
A(k ) = A(k −1) M (n−k ) ,
где матрица М(n – k) отличается от единичной только (n – k)-й строкой, компоненты которой равны
Mn(n−−kkj) = −
Mn(n−−kkn)−k =
A(k −1)
n−(k −1) j
A(k −1)
n−(k −1)n−k
1
A(k −1)
n−(k −1)n−k
, j =1, n ( j ≠ n −k);
(3.20)
.
Чтобы завершить k-е |
подобное |
|
преобразование |
необходимо |
|||||||||||||||
умножить промежуточную матрицу |
(k ) |
на матрицу (M |
(n−k ) |
) |
−1 |
||||||||||||||
A |
|
|
|
||||||||||||||||
(k ) |
= (M |
(n−k ) |
) |
−1 |
(k −1) |
M |
(n−k ) |
= (M |
(n−k ) |
) |
−1 |
(k ) |
. |
|
|
|
(3.21) |
||
A |
|
|
A |
|
|
|
|
A |
|
|
|
||||||||
Последняя получается из единичной матрицы подстановкой в ее (n – k)-ю строку компонент (п – (k – 1))-й строки матрицы A(k −1) .
Легко проверить, что в этом случае будет выполняться необходимое соотношение
(M (n−k ) )−1 M (n−k ) = E.
Матричная операция (3.20) приводит к изменению компонент
только одной (n – k)-й строки |
(k ) |
|
|
|
A |
|
|
|
|
n |
(k −1) |
(k ) |
|
|
(k ) |
, j =1,n, |
(3.22) |
||
An−k j = ∑An−(k −1) m Am j |
||||
m=1
76
или с учетом нулевых компонент в нижних подстолбцах матрицы
A(k )
n−k |
(k −1) |
(k ) |
, j =1, n −(k +1); j = n; |
||
∑An−(k −1) m Am j |
|||||
(k ) m=1 |
|
|
(3.23) |
||
An−k j = |
n−k |
|
|
||
|
(k −1) |
(k ) |
(k −1) |
||
|
|||||
∑An−(k −1) m Am j |
+ An−(k −1) j , j = (n −k),(n −1). |
||||
m=1 |
|
|
|
||
После построения характеристического полинома и нахождения его корней – собственных чисел матрицы A, легко определяются собственные вектора матрицы Р (y), а затем и матрицы А, так как
Py =λy (M −1 AM ) y = λyA(My) = λ(My) x = My.
где M = M (n−1) M (n−2) ...M (2) M (1) .
Для определения векторов у распишем систему
( p −λ) y + p y |
2 |
+... + p y |
n |
= 0; |
||
|
1 |
1 2 |
n |
|
||
|
|
y1 −λy2 |
|
|
|
= 0; |
................................................... |
||||||
|
|
|
|
|
|
|
|
|
|
|
yn−1 −λyn = 0. |
||
|
|
|
|
|||
(3.24)
(P −λE) y = 0
(3.25)
Положив уп = 1 (это можно сделать, так как собственные векторы определяются с точностью до постоянной), из последнего и последующих (до первого) уравнений легко находим
y ={yn =1, yn−1 = λ, yn−2 = λ2 ,..., y1 = λn−1}. |
(3.26) |
При таких значениях уi первое уравнение системы (3.25) удовлетворяется автоматически, поскольку оно совпадает с характеристическим уравнением (3.2).
Теперь с учетом вида матриц M (n−k ) |
|
|
|
|
||
1 |
0................... |
0 |
0 |
|
|
|
............................................... |
|
|
||||
|
|
|
|
|
|
|
M (n−k ) = M (n−k ) M (n−k ) ........ |
M (n−k ) |
M (n−k ) |
(3.27) |
|||
|
n−k1 |
n−k 2 |
n−k n−1 |
n−k n |
|
|
................................................ |
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
|
|
|
|
|
||||
77
легко рассчитываются компоненты собственных векторов х (первоначально устанавливается х = у)
n |
|
xn−k = ∑Mn(n−−kkj) xj , k = (n −1),1. |
(3.28) |
j=1
Остановимся на особенностях программной реализации данного метода.
1.Обрабатываемая матрица хранится на месте исходной.
2.Для повышения устойчивости алгоритма перед выполнением очередного k-го подобного преобразования необходимо выполнять процедуру выбора «ведущего» элемента: найти среди компонент
A(k −1) |
, j =1,(n −k), максимальный по модулю элемент и, если |
n−(k −1) j |
|
jmax ≠ (n − k) , то переставить местами верхние части столбцов и
строки с номерами (n – k) и jmax. Такая перестановка (TA(k −1)T ) будет подобной, поскольку для матрицы перестановок T справедливо соотношение Т–1 = Т. Если окажется, что «ведущий» элемент равен нулю, то имеет место сингулярный случай, когда характеристический полином распадается на произведение двух
характеристических полиномов: |
|
|
|
(n−k ) |
|
|
|
det(A −λE) = A |
−λE B |
|
= |
0 |
P(k ) −λE |
|
|
|
|
|
|
= det(A(n−k ) −λE) det(P(k ) −λE),
причем для одного из них матрица Фробениуса Р(k) уже получена, а для подматрицы A(n−k ) ее предстоит еще найти с помощью того же метода. В этом особом случае собственные векторы матрицы следует искать вне данного метода (см. п. 3.5).
3. Строку Mn(n−−kkj) , j =1,n, (см. формулы (3.20)) матрицы M (n−k )
можно первоначально формировать в дополнительном векторе т, а в конце k-го преобразования сохранять на месте (п – (k – 1))-й обработанной строки исходной матрицы. При этом формулы (3.18), (3.19) перепишутся следующим образом:
(k ) |
(k −1) |
|
(k −1) |
mj , i =1,(n − k), j =1, n ( j ≠ n − k); |
|
Ai j |
= Ai j |
|
+ Ai n−k |
||
(k ) |
|
(k −1) |
|
(3.29) |
|
|
mn−k , |
i =1,(n − k). |
|||
Ai n−k = Ai n−k |
|||||
78
Здесь исключена явная обработка (п – (k – 1))-й приводимой строки, поскольку ее компоненты используются при завершении k-го подобного преобразования (см. формулы (3.23)).
В соответствии с изложенным выше, была разработана программа, позволяющая построить матрицу Фробениуса для произвольной матрицы, а затем определить методом парабол корни характеристического полинома этой матрицы. Программа успешно работает и случаи вырождения маирицы Фробениуса в две и более подматриц. Скриншоты этой программы представлены на рис. 3.3 – 3.7. Обратите внимание, что, как и положено, сумма следов двух матриц Фробениуса равна следу исходной матрицы (21+7=28), а суммы корней каждой из подматриц совпадает с ее следом.
Ниже приведены листинги на Visual Basic алгоритма, вычисляющего матрицу Фробениуса, и прицедуры выбора ведущего элемента, используемой на каждом шаге алгоритма.
For k = 1 To n - 1 kk = kk + 1
If v_element(k) = 1 Then ‘выделена подматрица Фробениуса code = 1
Exit For End If
For j = 0 To n - 1
ma(j) = a(n - k, j) 'сохраняем обрабатываемую строку
Next j
'ставим 1 в обрабатываемой строке
For i = 0 To n - k
a(i, n - 1 - k) = a(i, n - 1 - k) / a(n - k, n - 1 - k) Next i
'ставим 0 вместо остальных элементов обрабатываемой строки
For i = 0 To n - k For j = 0 To n - 1
If Not (j = n - 1 - k) Then
a(i, j) = a(i, j) - a(i, n - 1 - k) * a(n - k, j) End If
Next j Next i
'умножаем на обратную матрицу (М) For j = 0 To n - 1
buf = 0
For m = 0 To n - 1
79
buf = buf + ma(m) * a(m, j) Next m
a(n - 1 - k, j) = buf Next j
Next k
Function v_element (k As Integer) As Integer Dim amax#, jmax%, i%, j%, buf#, cd%
cd = 0
amax = Abs(a(n - k, n - 1 - k)) jmax = n - 1 - k
For j = 0 To n - 2 - k buf = Abs(a(n - k, j)) If buf > amax Then
amax = buf jmax = j
End If Next j
If Not (k = jmax) Then For i = 0 To n - 1
buf = a(i, n - 1 - k)
a(i, n - 1 - k) = a(i, jmax) a(i, jmax) = buf
Next i
For j = 0 To n - 1
buf = a(n - 1 - k, j)
a(n - 1 - k, j) = a(jmax, j) a(jmax, j) = buf
Next j End If
If amax < 1E-30 Then cd = 1 code = cd
v_element = cd End Function
Здесь ma(n) – вспомогательный массив для временного хранения обрабатываемой строки; n – размерность обрабатываемой матрицы; v_element – функция, реализующая процедуру выбора ведущего элемента.
80

Рис. 3.3. Форма, с описанием порядка работы с программой
81
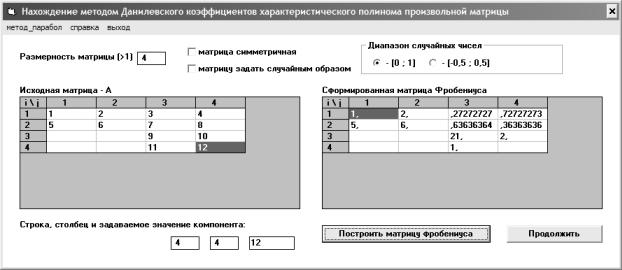
82
Рис. 3.4. Главная форма программы, на которой приведен пример матрицы, для которой матрица Фробениуса распадается на две подматрицы. Здесь приведен этап получения первой подматрицы
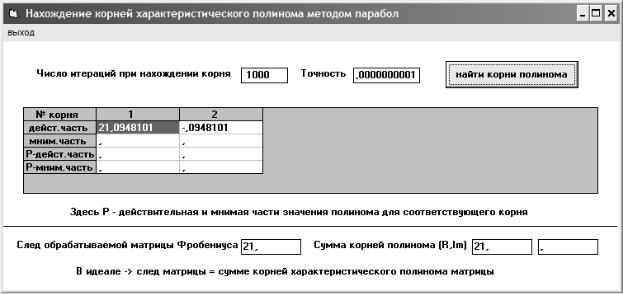
Рис. 3.5. Корни характеристического полинома, полученные методом парабол для первой подматрицы Фробениуса
83
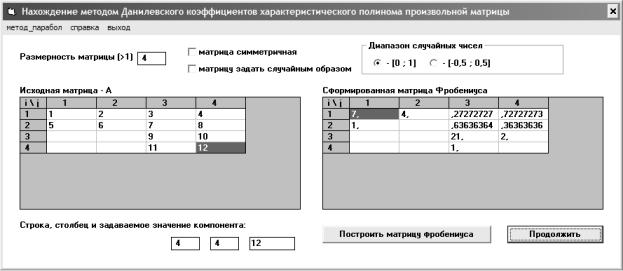
84
Рис. 3.6. Главная форма программы после получения второй подматрицы Фробениуса
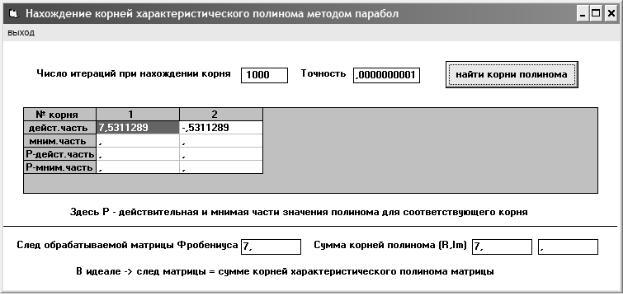
Рис. 3.7. Корни характеристического полинома, полученные методом парабол для второй подматрицы Фробениуса
85
