Михайлов Аналитическая геометрия 2008

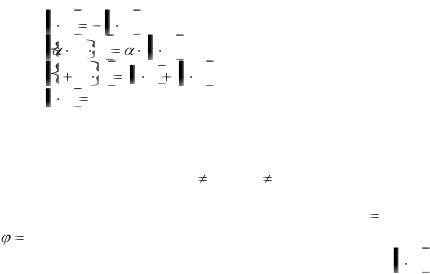
Определение 4.3. Упорядоченная тройка некомпланарных

	является	правой,	если, после	приведения
векторов a, b, c
векторов к общему началу,		вектор
			c располагается так,
что из его конца кратчайший поворот от a				к b виден

происходящим в направлении против часовой стрелки. (В противном случае тройка векторов считается левой.)

Это утверждение справедливо для тройки векторов i , j, k

и для системы декартовых координат в пространстве. Векторное произведение имеет следующие алгебраичес-

кие свойства:

1)					, (антиперестановочность)
	a	b	b	a
2)
		a	b			a	b ,
3)									,
	a	b	c	a		c	b	c

4)a a 0 .

Теорема 4.3. Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения.

Доказательство. Если a 0 и b 0 , то доказательство необходимости и достаточности утверждения теоремы следует из (4.12) и того факта, что условие sin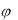 0 при

0 также является необходимым и достаточным.

Теорема 4.4. Модуль векторного
	произведения a	b
равняется площади S параллелограмма,	построенного	на

приведенных к общему началу векторах a и b .

Доказательство. Поскольку площадь параллелограмма равна произведению длин его смежных сторон на синус угла между ними, доказательство теоремы следует из формулы

(4.12).

Теорема 4.5. Если вектора представлены разложениями

но базису i , j, k

41

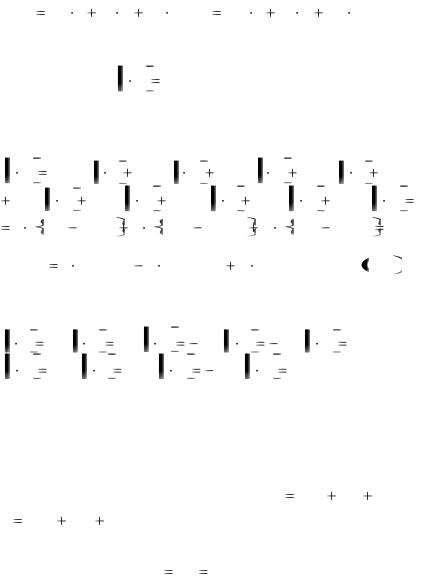
a	X1 i	Y1 j	Z1 k ,	b	X 2 i	Y2 j	Z2 k , (4.13)

то их векторное произведение имеет вид:

i

j

k

(4.14)

a b

X1

Y1

Z1

X 2

Y2

Z 2

Доказательство. Перемножив векторные многочлены

(4.13), получим, что

a b

X1 X 2 i i

X1Y2 i j X1Z 2 i k Y1 X 2 j i

Y1Y2 j j Y1Z 2

j k Z1 X 2 k i Z1Y2

k j Z1Z 2 k k

i Y1Z 2

Y2 Z1

j Z1 X 2

Z 2 X1

k X1Y2

X 2Y1

Y

Z

1

X

1

Z

1

X

1

Y

i

1

j

k

1

4.15

Y2

Z 2

X 2

Z 2

X 2

Y2

Строка (4.15) последнего выражения получена с учетом

того, что

i i

0, i j

k , i k

j ,

j i

k ,

j j

0,

(4.16)

j k

i ,

k i

j ,

k j

i ,

k k

0.

(Знак

минус в

этих произведениях

получается вследствие

нарушения порядка в тройке ортов

i

j k .)

Очевидно, что выражение (4.15) есть разложение

определителя (4.14) по элементам первой строки.

Теорема доказана.

Если

два

вектора

и

Следствие.

a

X1i

Y1 j

Z1k

b

X

2i

Y2 j

Z2 k коллинеарны,

то

координаты

их

пропорциональны, т.е.

X1

Y1

Z1

.

(4.17)

X 2

Y2

Z 2

42

Доказательство. Поскольку векторное произведение коллинеарных векторов равно нулю, из соотношения (4.15) следует, что

Y1Z2 Y2 Z1,	Z1 X 2			Z2 X1,	X1Y2			X 2Y1 (4.18)
Из первого равенства после деления на произведение Y2 Z 2
получим пропорцию	Y1		Z1	. Аналогичным образом из
	Y2		Z 2
второго равенства получаем пропорцию						Z1		X1	.
						Z 2		X 2

Следствие доказано.

Впропорции (4.17) возможно появление нулей в знаменателе.

Всоответствии с (4.18) это означает, что соответствующий числитель тоже равен нулю.

Для		последующих	выкладок нам		удобно	считать,
что a	b	d .
Следствие 1. Если				−орт вектора
			e		d , а S		a	b
				d

−площадь параллелограмма, построенного на перемножаемых векторах, приведенных к общему началу, то

S

(4.19)

d

a

b

e

e

d

d

Определение 4.4.

Если

векторное

произведение

a

b

умножить скалярно

на

вектор

то

число

c ,

a b

c

называется смешанным произведением векторов

a, b и c .

равно

Теорема 4.6. Смешанное произведение a

b

c

объѐму параллелепипеда, построенного на приведенных к

общему началу векторах a, b

и c , взятому со знаком плюс,

если тройка векторов правая, и со знаком минус, если тройка

abc левая. Если же перемножаемые вектора компланарны,

43

то их смешанное произведение ровно нулю.

			d
				c
	Ïð	d c	h
			e
			d			b
						a
				Рис. 4.1
Доказательство.			Тривиальный			случай коллинеарности
векторов			исключим, так как векторное произведение
	a	и b

коллинеарных векторов равно нулю. Тогда, используя

выражение				(4.19),			можно	произвести		следующее
преобразование
									h	V . (4.20)
a	b	c	d	c S	e		c S Ïð	c S
					d			d

(Знак + берем в случае, если тройка векторов правая).

Если же вектора			и		компланарны,			то вектор			лежит в
	a, b			c						c
плоскости векторов			a	и	b ,	следовательно h Ïð					d c 0 и
V S h 0 .
Теорема доказана.
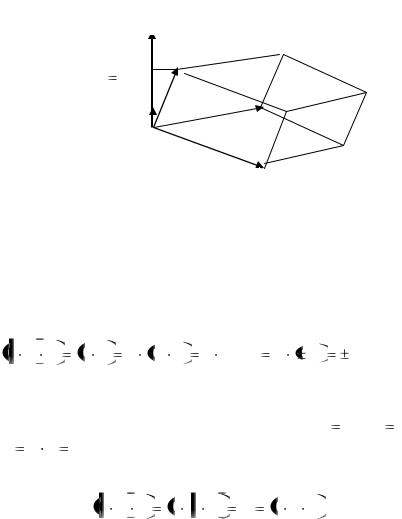
Следствие 1. Справедливо равенство
											(4.21)
a	b	c		a	b	c	V a	b	c

Объѐм параллелепипеда не зависит от того, какая пара векторов из тройки перемножается векторно. Знак

44

произведения не изменяется, так как сохраняется порядок векторов и ориентация тройки векторов.

Следствие 2. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их

смешанного произведения.

Теорема

4.7.

Если

три

вектора

представлены

разложениями по базису i ,

j , k

a i X1

jY1

kZ1 , b i X 2

jY2

kZ2 , c i X 3

jY3

kZ3 ,

то их смешанное произведение равно следующему определителю:

X1

Y1

Z1

a

b

c

X 2

Y2

Z 2

(4.22)

X 3

Y3

Z3

Доказательство. Из формулы (4.15) следует, что:

Y

Z

1

X

1

Z

1

X

1

Y

1

1

a b i

Y2

Z 2

j

X 2

Z 2

k

X 2

Y2

Умножив скалярно этот вектор на вектор c , получим,

Y1

Z1

X1

Z1

X1

Y1

(4.23)

a b

c

X 3

Y

Z

2

Y3

X

2

Z

2

Z3

X

2

Y

2

2

Полученное выражение (4.23) есть разложение определителя (4.22) по элементам третьей строки. Теорема доказана.

Задачи № 795, 800, 803, 812, 818, 820, 829, 834, 840, 847, 851, 858, 875, 877.

§ 5. Прямая линия на плоскости

Определение 5.1. Уравнение

F x, y 0

(5.1)

называется уравнением линии на плоскости относительно заданной системы координат, если ему удовлетворяют координаты точек, принадлежащих некоторой линии L , и не

45

удовлетворяют координаты точек, не принадлежащих этой линии.

Определение 5.2. Линия называется алгебраической, если в некоторой прямоугольной системе координат F x, yесть

полином некоторой степени.

Алгебраическая линия называется линией n - го порядка если F x, y− полином степени n .

Теорема 5.1. Если линия в некоторой прямоугольной системе координат определяется алгебраическим уравнением степени n , то и в другой прямоугольной системе координат степень уравнения будет равна n .

Без доказательства.

В трехмерном пространстве определения 5.1 и 5.3 и утверждение теоремы 5.1 можно повторить, заменив слово линия словом поверхность.

Теорема 5.2. Если на плоскости фиксирована прямоугольная система координат Oxy , то любая прямая L ,

принадлежащая плоскости, определяется в этой системе координат уравнением первой степени.

Доказательство. При специальном выборе системы

координат,	если	ось Ox совпадает с прямой, уравнение
прямой « y	0 »	совпадает с уравнением оси Ox . В

соответствии с утверждением теоремы 5.1 в любой другой прямоугольной системе координат степень уравнения сохранится.

Пусть уравнение прямой имеет вид:

A x B	y C	0 ,		A		B	0	(5.1)
Пусть задана	точка	M 0	x0 , y0			,	координаты	которой

удовлетворяют уравнению.

A x0 B y0 C 0 .

(5.2)

Вычитая (5.2) из (5.1), получаем:

A x x0 B y y0 0 .

(5.3)

46

Дадим векторное истолкование уравнения (5.3).

	Пусть								A, B	,
		A и B − координаты некоторого вектора n
а	x		x0		и	y y0	−компоненты		вектора
M 0 M		x	x0 ,	y y0		, начало которого		совпадает		с
точкой M 0			x0 , y0	, а конец совпадает с произвольной точкой
M x, y , принадлежащей прямой.
	Очевидно, что скалярное произведение
		n M 0 M A x x0					B y y0 0
								и M 0 M .
является условием ортогональности векторов n
			A, B называется нормальным вектором прямой.
Вектор n
					n			L

M

M 0

Рис. 5.1

Уравнение (5.3) есть уравнение прямой, проходящей через
точку M 0 x0 , y0 перпендикулярно вектору		. Уравнение
	n

(5.3) эквивалентно уравнению (5.1), которое называется

общим уравнением прямой.

При условии	A		B		0 рассмотрим неполные уравнения
прямой.
1). C 0 . Уравнение					A x B y 0 определяет прямую,

проходящую через начало координат.

47

2)	A	0 . Уравнение B y		C	0	определяет уравнение
прямой, параллельной оси Ox .
3)	B	0 . Уравнение A x		C	0	определяет уравнение
прямой, параллельной оси Oy .
4)	A	0, C	0 . Уравнение B y		0 определяет уравнение
оси Ox .
5)	B	0, C	0 . Уравнение A x		0 определяет уравнение

оси Oy .

Из уравнения (5.1) можно получить уравнение прямой в

отрезках.

x

y

1

(5.4)

a

b

В самом деле, уравнение

x

y

1

(5.5)

C

C

A

B

получено из уравнения (5.1) с помощью элементарных алгебраических преобразований.

Обозначив a CA , b CB , получим уравнение (5.4).

Чтобы найти координаты точки пересечения прямой с осью Ox , решим систему уравнений, состоящую из уравнения (5.4) и уравнения оси Ox .

	x		y	1	x
						1 x a .	(5.6)
	a		b
					a
		y		0

Аналогично можно получить, что y b координата точки пересечения с осью Oy .

Определение 5.3. Любой ненулевой вектор, параллельный данной прямой будем называть направляющим вектором прямой.

48

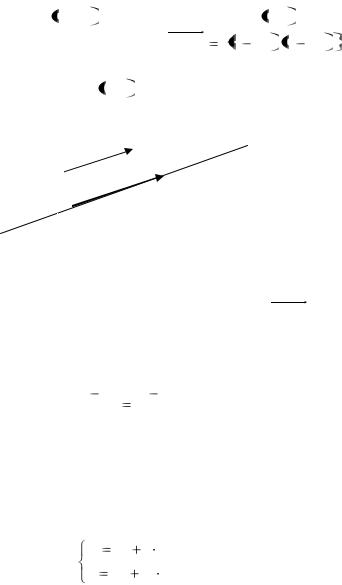
Задача 5.1. Составить уравнение прямой L , проходящей

через точку M1 x1 , y1 параллельно вектору q l, m .
Решение. Рассмотрим вектор M1M			x	x1 , y y1 ,
начало которого совпадает с точкой M1 , а конец − в
произвольной точке M x, y .
	q
				L
	M
M1
Рис. 5.2
Чтобы точка M лежала на прямой L ,			вектор M1M должен
				параллельности
быть параллелен вектору q . Условие

векторов состоит в пропорциональности сходственных координат, из чего следует

x x1		y y1	.	(5.7)
l		m

(Нуль в знаменателе в этой пропорции означает, что соответствующий числитель тоже обращается в нуль.)

Это уравнение называется каноническим уравнением прямой.

Приравняв выражение (5.7) параметру t , получим

параметрические уравнения прямой.

x	x1	l	t		(5.8)
y	y1	m		t

49

Если принять что, t −время, а				вектор скорости,
	v	i l	j m

то уравнения (5.8) определяют две проекции уравнения движения точки на координатные оси.

Уравнение прямой, проходящей через две заданные точки

M1 x1 , y1 и M 2 x2 , y2			получим из уравнения (5.7), приняв,
что направляющий вектор
									(5.9)
q	M1M 2			x2	x1	y2		y1
и подставив выражение (5.9) в (5.7):
		x	x		y	y1			(5.10)
		x2	x1		y2	y1
Уравнение	прямой		с		угловым			коэффициентом k

получим, приняв, что угловой коэффициент равен тангенсу

угла наклона направляющего вектора q :

	k tg	m	(5.11)
		l

y

L

b

q

m

x

l

Рис. 5.3

Умножив выражение (5.7) на число m и подставив в него

(5.11), получим:

50