Федоров Однофотонная вычислителная томография 2008

	1		+∞ 2π		1	+∞	1
=			∫	∫e−irρcos(ϕ−ψ)drdϕ =		∫J0 (rρ)dr =		,
	2π	2			π		πρ
			0	0		0

где J0 – функция Бесселя нулевого порядка.

При выводе этой формулы были использованы соотношения:

1	2πe−irρcos(ϕ−ψ)dϕ = J0 (rρ)	и	+∞J0 (x)dx =1.
2π ∫			∫
0			0

Таким образом, для фурье-образа H2 (ρ,ϕ) = H2 (ρ) ядра h2 (x, y) получили следующие выражения:

H2 (ρ) =1/ πρ или H2 (u, v) =1/ π u2 + v2 .

Применение буквы ρ (ро) и дало название рассмотренному методу – метод ро-фильтрации.

Поскольку фурье-образ H2 (ρ) ядра h2 (x, y) зависит только от радиуса ρ, аподизирующую функцию естественно выбирать зави-

сящей только от ρ: A2 (u,v) = A2 (ρ,ψ) = A2 (ρ).

В качестве окна могут быть использованы функции в виде прямоугольного импульса, ограниченного по полосе частот, косинусную, синусную, а также обобщенную функцию Хемминга:

A2	1				при 0 ≤ ρ ≤ ρ0 ,
	(ρ) =				при ρ > ρ0 ;
	0
A2	cos(πρ 2ρ0 )				при 0 ≤ ρ ≤ ρ0 ,
	(ρ) =				при ρ > ρ0 ;
	0
	sin(πρ 2ρ0 )				при 0 ≤ ρ ≤ ρ0 ,
A2			πρ 2ρ0
	(ρ) =
					при ρ > ρ0 ;
	0

41

A2	α + (1 − α)cos(πρ ρ0 )	при 0 ≤ ρ ≤ ρ0 и 0 ≤ α ≤1,
	(ρ) =	при ρ > ρ0.
	0

Последнюю аподизирующую функцию называют при α = 0,5 хэннинговым окном, а при α = 0,54 – окном Хемминга.

Недостатком метода ро-фильтрации является необходимость выполнения всего цикла измерений до начала обработки полученной информации. От этого недостатка свободны два других метода, рассмотренных в этой главе.

2.5. Метод фурье-синтеза

Метод обращения основан на так называемой теореме о центральном сечении, устанавливающей связь между одномерным фу- рье-образом проекции p(ξ,θ) по переменной ξ и двумерным фу-

рье-образом искомого распределения µ(x, y) .

Запишем выражение для проекции(2.5) вполярныхкоординатах

+∞2π
p(ξ,θ)= ∫∫µ(r,ϕ)δ(ξ − r cos(θ − ϕ))rdrdϕ	(2.18)

00

иопределим одномерный фурье-образ проекции по переменной ξ:

		P(χ,θ)= F {p(ξ,θ)}=						1	+∞p(ξ,θ)e−iξχdξ =
					1			2π	∫
									−∞
	1		+∞ 2π +∞			µ(r,ϕ)δ[ξ − r cos(θ − ϕ)]e−iξχrdrdϕdξ =
=			∫	∫	∫
	2π		0	0	−∞
					1	+∞ 2π
				=		∫ ∫µ(r,ϕ) e−iχr cos(θ−ϕ)rdrdϕ.
					2π	0	0

42

Аналогично найдем двумерный фурье-образ искомого распределения µ(r,ϕ) :

			+∞ 2π
		2π ∫		∫
F {µ(r,ϕ)} = M (ρ,ψ) =		1			µ(r,ϕ)e−irρcos(ψ−ϕ)r dr dϕ.	(2.19)
2
			0	0
Очевидно, если χ заменить ρ и θ заменить ψ , получим
	M (ρ,ψ) = (1 2π)P(ρ,ψ) .					(2.20)

Соотношение (2.20), играющее ключевую роль в РВТ, и является теоремой о центральном сечении. Одномерный фурье-образ проекции, полученной при повороте системы «источник–детектор» на угол θ , является сечением двумерного фурье-образа искомого двумерного распределения по линии, проходящей через начало координат (центральным сечением) и повернутой на угол θ. Таким образом, из одномерных фурье-образов проекций синтезируют двумерный фурье-образ искомого изображения, которое затем можно восстановить с помощью двумерного обратного преобразования Фурье. Это обстоятельство делает понятной роль многоракурсности просвечивания в диапазоне углов не менее 180° и способности метода РВТ восстанавливать локальные характеристики сложной внутренней структуры без взаимного наложения, характерного для неполных проекционных данных (малоракурсного просвечивания). Кроме того, рассматриваемый алгоритм реконструкции, основанный на двумерном преобразовании Фурье, относится к наиболее быстрым из известных алгоритмов, и позволяет начинать обработку экспериментальных данных в процессе измерений.

Запишем (2.20) в виде

F2{µ(x, y)} = (1 2π)P(ρ, ψ)	(2.21)
или
µ(x, y) = (1 2π)F −1{P(ρ,ψ)}.	(2.22)
2

Специфика метода фурье-синтеза заключается в том, что отсчеты фурье-образа M (ρ,ψ) искомой функции µ(x, y) находятся на

43

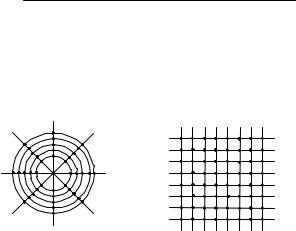
полярной сетке (рис. 2.6), а обратное преобразование Фурье необходимо выполнять на декартовой сетке с использованием быстрого преобразования Фурье (БПФ).

Поэтому декартовы отсчеты M (u,v) находят путем интерполяии полярных отсчетов M (ρ,ψ) . Простейшие алгоритмы – полино-

миальные алгоритмы нулевого и первого порядка. При интерполяции нулевого порядка интерполированное значение равно значению ближайшего отсчета. Однако лучшее качество реконструкции дает интерполяция первого порядка.

При этом используется, как правило, линейная интерполяция по ближайшим четырем отсчетам:

Mд = (Mп1 / d1) + (Mп2 / d2 ) + (Mп3 / d3 ) + (Mп4 / d4 ) , (1/ d1) + (1/ d2 ) + (1/ d3 ) + (1/ d4 )

где Mд – декартов отсчет; Mп1 ,…, Mп4 – полярные отсчеты; d1 , ..., d4 – расстояния от декартова отсчета до соответствующих полярных отсчетов.

а) б)

Рис. 2.6. Полярная (а) и декартова (б) сетки отсчетов

Таким образом, метод фурье-синтеза включает в себя следующую последовательность действий:

(БПФ)1 → формирование (ФО)2 → интерполяция → (БОПФ)2,

т.е. быстрое одномерное преобразование Фурье каждой проекции и формирование двумерного фурье-образа на полярной сетке, интерполяция отсчета двумерного фурье-образа на полярной сетке для

44

получения отсчетов на декартовой сетке, быстрое двумерное обратное преобразование Фурье для получения конечного изображения.

Представляется естественным использовать для реконструкции изображений непосредственно формулу (2.22). Но небольшие погрешности в фурье-пространстве, возникающие в основном при переходе из полярной M (ρ,ψ) в прямоугольную M (u,v) систему ко-

ординат, приводят к появлению масштабных искажений в пространственной области. Чтобы избежать появления артефактов на изображении необходимо принимать специальные меры, описанные в литературе.

Рассмотрим возможность иного решения (2.22), опустив на этом этапе в формулах для простоты постоянные коэффициенты. Приведенный ниже алгоритм – одномерная фильтрация проекций с последующим обратным проецированием обладает большой вычислительной устойчивостью и более детально рассмотрен в следующем разделе.

Чтобы найти двумерное преобразование Фурье от (2.20) относительно u и v, перейдем к переменным интегрирования χ и θ и уч-

тем, что dudv = χdχdθ. В результате получим

2π	+∞
µ(x, y) = ∫dθ ∫dχ			χ		P(θ,χ)eiχξ		ξ=x cos θ+ y sin θ.	(2.23)
0	−∞

Согласно теореме Бореля о свертке:

F[f1(t) f2 (t)]= F[f1(t)] F[f2 (t)],

F[f1(t)] F[f2 (t)]= F[f1(t) f2 (t)],

такими функциями в (2.23) являются фурье-образы χ и P(θ,χ) со-

ответственно ядра и проекции. В пространственной области ядро выражается как

+∞

h1(ξ) = ∫χ eiχξdχ ,

−∞

а формула (2.23) преобразуется к виду

45

2π
µ(x, y) = ∫dθ p(θ,ξ) h1(ξ)		ξ=x cosθ+ y sin θ .	(2.24)
0

Таким образом, проекционные данные p(θ,ξ) необходимо сначала свернуть с ядром реконструкции (фильтром) h1(ξ) , а затем выполнить операцию обратного проецирования.

2.6. Метод фильтрованных обратных проекций (метод одномерной фильтрации)

В методе ρ-фильтрации на первом этапе выполнялось обратное проецирование, а полученное суммарное изображение подвергалось двумерной фильтрации, результатом которой являлась оценка искомого изображения. В методе фильтрованных обратных проекций последовательность действий обратная. Сначала осуществляется одномерная фильтрация каждой проекции, после чего производится операция обратного проецирования, результатом которой является оценка искомого изображения. Этот метод оказался весьма эффективным в вычислительном отношении, и его варианты широко используются практически во всех современных коммерческих рентгеновских томографах.

Запишем выражение для отфильтрованной проекции в следующем виде:

f (ξ,θ)= +∞∫p(ξ0 , θ)h1 (ξ−ξ0 )dξ0 .	(2.25)
−∞

В приведенном выражении использована одномерная функция ядра свертки h1(ξ), которая пока неизвестна и подлежит определе-

нию. На втором шаге нужно произвести операцию обратного проецирования, т.е. найти обратную проекцию согласно (2.7) и получить суммарное изображение, которое должно сразу же являться оценкой искомого распределения µ(x, y):

		1	2π	1	2π
	µ(x, y) =		∫b(x, y,θ)dθ =		∫ f (x cosθ + y sin θ,θ) dθ .
		2π		2π
			0		0

46

Подставляя в эту формулу выражение для отфильтрованной проекции (2.25) и проекции (2.5), получим

1

2π

+∞

µ(x, y) =

∫dθ ∫p(ξ0 ,θ)h1(x cosθ + y sin θ − ξ0 )dξ0 =

2π

0

−∞

1

2π +∞

=

dθ

h (xcosθ + y sin θ − ξ )dξ

×

2π ∫

∫

1

0

0

0

−∞

×

+∞ +∞

µ(x

, y

)δ(ξ

− x

cosθ − y

sin θ)dx dy

=

∫ ∫

0

0

0

0

0

0

0

−∞ −∞

+∞ +∞

1

2π

=

∫ ∫

µ(x , y

)dx dy

h ((x − x )cosθ + (y

− y

)sin

θ)dθ .

2π

0 0

0 0

∫ 1

0

0

−∞ −∞

0

(2.26)

Нетрудно определить, что имеет место тождество при условии

1	2∫πh1(x cos θ+ y sin θ)dθ = δ(x)δ( y) .	(2.27)
2π
	0

Таким образом, соотношение (2.27) является определением обобщенной функции ядра h1(ξ). Найдем ее фурье-образ H1(χ),

выразив h1(ξ) через обратное одномерное преобразование Фурье H1(χ), а δ(x)δ( y) – через обратное двумерное преобразование Фурье:

				1	+∞
			h (ξ) =		∫		H (χ) e iχξdχ ,
			1	2π				1
					−∞
	1		+∞ +∞					1	+∞ 2π
δ(x)δ( y) =			∫ ∫e i(ux+vy)dudv =						∫ ∫e iρ(x cos ψ+ y sin ψ)ρdρdψ.
	(2π)	2						2
			−∞ −∞			(2π)			0 0

Подставив эти выражения в равенство (2.27), получим

47

1	2π +∞			1					+∞ 2π
	∫ ∫	H1	(χ) e iχ( x cos θ+ y sin θ)dθdχ =						∫ ∫	e iρ( x cos ψ+ y sin ψ)ρdρdψ.
(2π)3 / 2				(2π)2
	0 −∞								0 0
Если положить H1 (− χ)= H1 (χ), видно, что
			H1(χ) = (2 2π)−1			χ		.		(2.28)

Функция ядра в фурье-пространстве дается формулой (2.28), а для функции ядра в координатном пространстве можно дать интегральное представление:

h (ξ) =

1

+∞

χ

eiχξdχ = −

1

Ξ

1

,

(2.29)

1

4π

∫

2π

ξ2

−∞

где Ξξ −2

– обобщенная функция, действующая по правилу

1

+∞

1

+∞

f

(ξ) − f

(0)

∫ Ξ

f (ξ) dξ ≡ v.p. ∫

Ξ

,

f (ξ)

=

dξ =

ξ

2

ξ

2

ξ

2

−∞

−∞

+∞

f

′

= v.p.

∫

(ξ)

dξ,

ξ

−∞

где v.p. – знак интегрирования в смысле главного значения Коши. Тогда, используя формулу обращения в соответствии с (2.26)

1

2π

+∞

µ(x, y) =

∫

dθ

∫

p(ξ ,θ)h (xcosθ + y sin θ − ξ )dξ ,

2π

0

1

0

0

найдем

0

−∞

2π +∞

1

1

1

µ(x, y) =

∫ ∫ p(ξ,θ) −

Ξ

dξdθ =

2π

2π

(x cosθ + y sin θ − ξ)

2

0 −∞

	1		2π	+∞		p(ξ,θ) − p(0,θ)
=			v.p.	−∞∫				dξdθ =
	(2π)	2				(x cos θ+ y sin θ−ξ)	2
			∫0

48

	1	2π		+∞	1	dp(ξ,θ)
		∫		∫
=			v.p.					dξdθ.
	(2π)2						dξ
					(xcosθ + y sin θ − ξ)
		0		−∞

Полученная формула является обратным преобразованием Радона, полученным самим И. Радоном, и приведена в пособии ранее

(см. формулу (2.6)).

Так же, как и в методе ρ-фильтрации, можно ввести аподизирующую функцию A1(χ) :

	h (ξ) =	1	+∞	χ		eiχξA (χ)dχ .	(2.30)
			∫
		4π
	1					1

−∞

В качестве аподизирующих могут быть использованы практически те же (если ρ заменить χ ) функции, что и в методе ро-

фильтрации, приведенные в разд. 2.4:

A1(χ) =	1
	0
A1(χ) =	cos(πχ 2χ0 )
	0
	sin(πχ 2χ0 )
A (χ) =		πχ 2χ0
1
	0
A1(χ) =	α + (1−α) cos(πχ χ0 )
	0

при	0 ≤ χ ≤ χ0 ,
при	χ > χ0 ;
при	0 ≤ χ ≤ χ0 ,
при	χ > χ0 ;
при	0 ≤ χ ≤ χ0 ,
при	χ > χ0 ;

при 0 ≤ χ ≤ χ0 и 0 ≤ α ≤1,

при χ > χ0.

Выбор аподизирующих функций такого вида не случаен и может быть увязан с функцией передачи модуляций (ФПМ), отражающей отклик в фурье-пространстве измерительной системы на бесконечную линейную структуру, перпендикулярную плоскости проецирования. Например, при визуализации с использованием точечного рентгенов-

49

скогоисточникаидетектораширинойw внаправлениипроекцииФПМ имеет вид (sin πχw) /(πχw) . Аналогичный вид, без учета эффекта мас-

штабирования, имеет ФПМ при точечном детекторе и фокусном пятне рентгеновской трубки в виде квадрата шириной w. Это объясняет эффективность использования фильтра в виде прямоугольного импульса, ограниченного по полосе частот. Однако в реальных томографах помимо того, что источник и детектор имеют конечные размеры, вклад рассеянного излучения и другие факторы приводят к дополнительному уменьшению ФПМ в области высоких частот. Поэтому иногда полезно уменьшить вклад высоких частот в изображение, чтобы снизить влияние шумов, и на практике применяют другие приведенные ядра. Помимо стандартного ядра свертки используют также ядра, сильно слаживающие или слаживающие изображение, ядра высокого разрешения и ядра, подчеркивающие контуры, а также промежуточные модификации.

Рассмотрим первую из приведенных выше аподизирующих функций. Подставив ее в (2.30), получим

+∞

+χ0

χ0

∫

4π

∫

2π ∫

h (ξ) =

χ

eiχξA (χ)dχ =

1

χ

eiξχdχ =

1

χcos(χξ)dχ =

1

1

−∞

−χ0

0

1

χ

sin(χ

ξ)

cos(χ

ξ) −1

χ2

1

sinc2

χ

ξ

=

0

0

+

0

=

0

sinc(χ

ξ) −

0

,

2π

ξ

ξ

2

0

2

2

2π

где sincx ≡ (sin x) / x .

(2.31)

2.7. Алгебраические методы

При использовании аналитических методов решения дискретизация производится только на конечной стадии при численной реализации алгоритма, полученного в непрерывной форме. В алгебраических методах задача сразу рассматривается как дискретная, и дальнейшее описание проводится только в дискретной форме.

Тогда алгоритм получения изображения в вычислительной томографии сводится к решению системы линейных алгебраических уравнений (СЛАУ) или реже к системе нелинейных уравнений.

50