Сандаков Приведение кривых и поверхностей второго порядка к каноническому виду Учебно-методическое пособие 2009

Е.Б. Сандаков, В.П. Трифоненков, М.В. Смоленцев

ПРИВЕДЕНИЕ КРИВЫХ

ИПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА

ККАНОНИЧЕСКОМУ ВИДУ

Учебно-методическое пособие

Москва 2009

0

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

МОСКОВСКИЙ ИНЖЕНЕРНО-ФИЗИЧЕСКИЙ ИНСТИТУТ (ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ)

Е.Б. Сандаков, В.П. Трифоненков, М.В. Смоленцев

ПРИВЕДЕНИЕ КРИВЫХ

ИПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА

ККАНОНИЧЕСКОМУ ВИДУ

Учебно-методическое пособие

Москва 2009

1

УДК 514.12(07)

ББК 22.151.3я7

С 18

Сандаков Е.Б., Трифоненков В.П., Смоленцев М.В. Приведение

кривых и поверхностей второго порядка к каноническому виду:

учебно-методическое пособие. – М.: МИФИ, 2009. – 32 с.

Пособие «Приведение кривых и поверхностей второго порядка к каноническому виду» предназначено для студентов МИФИ первого курса всех специальностей. Оно полностью соответствует программе курса «Аналитическая геометрия», предусмотренного для таких технических и экономических вузов с углубленным изучением высшей математики, как МИФИ.

Состоит из двух параграфов. В первом параграфе рассматривается приведение кривых второго порядка к каноническому виду, а во втором – приведение поверхностей второго порядка к каноническому виду. В начале каждого параграфа приводятся краткие теоретические сведения (подробные сведения можно найти в пособии [1]). Затем разбирается большое число примеров приведения кривых и поверхностей второго порядка к каноническому виду.

Рецензент канд. физ.-мат. наук, доц. С.Г. Артышев

Рекомендовано к изданию редсоветом МИФИ

ISBN 978-5-7262-1134-3	© Московский инженерно-физический институт
	(государственный университет), 2009

2

	ОГЛАВЛЕНИЕ
§ 1.	Приведение кривых второго порядка
	к каноническому виду.................................................................	4
§ 2.	Приведение уравнения поверхности второго порядка
	к каноническому виду ...............................................................	18
Рекомендуемая литература...............................................................		30

3

§ 1. Приведение кривых второго порядка к каноническому виду

Общим уравнением линии второго порядка называется уравнение вида

a x2	2a	xy	a y2	2a	x 2a	23	y	a	0 ,		(1.1)
11	12		22	13				33
в котором по крайней мере один из коэффициентов a11, a12										, a22	отли-
чен от нуля (т.е.	a2	a2	a2	0).	Коэффициенты				a , a , a		22	на-
	11	12	22						11	12

зываются коэффициентами группы старших членов, коэффициенты a13 , a23 и a33 – коэффициентами линейной части уравнения (1.1).

Коэффициент a33 также называют свободным членом уравнения

(1.1).

Поставим следующую задачу. Найти такую декартовую систему координат, в которой уравнение (1.1) примет настолько простой вид, что геометрическая характеристика линии, определяемой этим уравнением, не будет представлять затруднений. Так как переход от одной декартовой прямоугольной системы координат к другой может быть осуществлен некоторым параллельным переносом системы координат и последующего поворота, то для решения поставленной задачи необходимо знать, как преобразуются коэффициенты уравнения (1.1) при параллельном переносе и повороте.

Как известно, старые (x, y) и новые (x , y ) координаты точки M при

	параллельном переносе связаны соотношениями:
	x x0	x ;	(1.2)
	y y0	y .

Подставляя выражения (1.2) для x и y в левую часть (1.1), получаем уравнение линии в системе O x y . Очевидно, это уравнение имеет вид:

a (x )2		2a	x y	a	22	( y )2		2a		x		2a	23	y		a		0 ,	(1.3)
11		12						13									33
где
			a13		a11x0			a12 y0			a13;
			a23		a12 x0			a22 y0			a23;								(1.4)
a	a x2		2a x y a y2						2a x 2a						23	y	0	a .
33	11	0	12	0	0		22	0			13	0						33

4

Осуществляя параллельный перенос координат, новое начало O (x0 , y0 ) иногда можно выбрать так, чтобы в уравнении (1.3) исчезли

члены первой степени, т.е. так, чтобы коэффициенты a13 и a23							равня-
лись нулю:
	a11x0	a12 y0		a13	0;		(1.5)
	a12 x0	a22 y0		a23	0.
Тогда уравнение (1.3) примет в новой системе O x y вид:
a (x )2	2a	x y a	22	( y )2	a	0 .	(1.6)
11	12				33

Очевидно, если (a, b) – произвольная точка, принадлежащая линии, определяемой уравнением (1.6), то и симметричная ей относительно

O точка ( a,	b) лежит на этой линии, т.е.	все точки данной линии
располагаются	симметрично относительно	точки O . Точка

O (x0 , y0 ) , обладающая указанным свойством, называется центром данной линии.

Таким образом, для нахождения координат (x0 , y0 ) центра данной

линии необходимо найти решение системы (1.5).

Уравнения (1.5) называются уравнениями центра линии второго порядка.

Если уравнения центра имеют единственное решение, то линию второго порядка называют центральной. В силу теоремы Крамера имеем: для того, чтобы кривая, определяемая уравнением (1.1), была центральной, необходимо и достаточно, чтобы определитель системы

(1.5) J	2	a11	a12	был отличен от нуля.
		a12	a22

Рассмотрим далее поворот декартовой прямоугольной системы координат на угол .

Как известно, поворот системы координат на угол задается фор-

	мулами
	x	x cos	y sin ;	(1.7)
	y	x sin	y cos .

Подставляя выражения (1.7) для x и y в левую часть (1.1), получаем уравнение линии в новой системе O x y . Очевидно, это уравнение имеет вид:

5

a (x )2	2a x y	a	22	( y )2	2a x	2a	23	y	a	0 ,	(1.8)
11	12				13				33
где

a

a

cos2

2a

cos

sin

a

sin2

;

11

11

12

22

a

a

cos

sin

a (cos2

sin2

)

a

22

cos sin

;

12

11

12

a

22

a

sin2

2a

cos

sin

a

22

cos2

;

(1.9)

11

12

a13

a12 cos

a23 sin

;

a23

a13 sin

a23 cos .

Всегда можно выбрать угол

поворота системы координат так,

чтобы после преобразования в уравнении (1.8) исчез член с произве-

дением текущих координат, т.е. так, чтобы в уравнении (1.8)

a12 0 .

Учитывая (1.9), для определения угла

получаем уравнение:

a sin2

(a

a

)sin

cos

a

cos2

0 .

12

11

22

12

Если a12

0 (иначе нет надобности в повороте систем координат), то

последнее уравнение приводится к виду

a

tg2

(a

a

) tg

a

0 .

(1.10)

12

22

11

12

Откуда

a

22

a

(a

22

a )2

4a2

tg

11

11

12

.

(1.11)

2a12

Отметим,

что tg 1

tg 2

1. Это означает, что для уравнения (1.1)

всегда найдутся два взаимно ортогональных направления, определяемые углами 1 и 2 , такие, что, поворачивая координатные оси на

один их этих углов, в новой системе координат получим уравнение линии, в котором отсутствует член с произведением текущих коорди-

нат (т.е. a12 0). После поворота на угол					, тангенс которого опреде-
лен по формуле (1.11), уравнение линии примет вид
a (x )2	a ( y )2		2a x 2a y a			0 .
11	22		13	23	33
Коэффициенты a11, a22 , a13		,	a23 определяют по формулам (1.9), пред-
варительно определив sin		и cos		по известному tg :
			6

sin		tg			cos			1			.	(1.12)
			;
	1 tg2				1				tg2

Знаки в знаменателях этих формул выбираются произвольно, но обя-

зательно одинаковыми.
	Как уже отмечалось, все кривые второго порядка подразделяются
на два больших класса:					центральные и нецентральные. Кривые, для
которых определитель					J2		a11	a12		0 , являются центральными, а
							a12	a22
кривые,			для которых		J2 0 ,			– нецентральными (или параболиче-
скими).
	Замечание. Нетрудно показать, что величины J2										a11 a22 и
J2		a11	a12	являются инвариантами линии второго							порядка (1.1)
		a12	a22

относительно преобразований декартовой прямоугольной системы координат.

Центральные кривые в свою очередь в зависимости от знака J 2

делятся еще на два класса: при	J2 0 кривые называются кривыми
эллиптического типа, а при J2	0 – кривыми гиперболического типа.

Итак, все линии второго порядка в зависимости от знака инварианта J 2 делятся на следующие три типа:

эллиптический тип, если J2	0 ;
гиперболический тип, если J2	0 ;
параболический тип, если J2	0 .

Очевидно, тип линии не меняется при изменении декартовой системы координат. Тогда справедлива следующая теорема.

Теорема. Для любой кривой второго порядка, заданной в декартовой прямоугольной системе координат Oxy уравнением (1.1), существует такая декартовая прямоугольная система координат O x y , в которой это уравнение принимает один из девяти видов:

1)	x2		y2	1		– эллипс (рис. 1);
	a2		b2
2)	x2		y2			1 – мнимый эллипс;
	a2		b2
						7

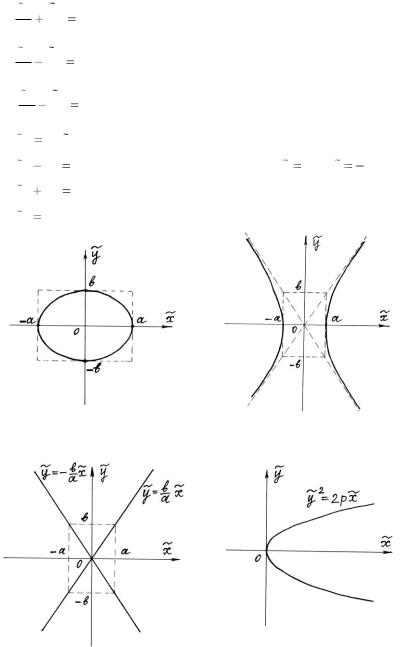
3)x2 a2

4)x2 a2

5)x2 a2

6)y2

7)y2

8)y2

9)y2

	y2			0	– одна точка;
	b2
	y2			1	– гипербола (рис. 2);
	b2
		y2		0	– пара пересекающихся прямых (рис. 3);
		b2
2 px – парабола (рис. 4);
a2				0 – пара параллельных прямых ( y a и y a );
a2				0 – пара мнимых параллельных прямых;

0 – пара совпавших прямых.

Рис. 1

Рис. 2

Рис. 3

Рис. 4

8

Рассмотрим примеры приведения кривых второго порядка к каноническому виду. Для этого рассмотрим отдельно случай центральной линии и случай нецентральной линии (параболический случай).

I. Случай центральной линии

Пример 1.1. Привести к каноническому виду уравнение линии второго порядка 5x2 8xy 5y2 18x 18y 9 0 и построить ее относительно первоначальной системы координат.

Решение. Отметим, что в случае центральной линии (J2 0) на

практике удобнее сначала сделать параллельный перенос системы координат в центр, а затем поворот системы координат вокруг центра. В

	нашем случае	J2	5	4	9 .
			4	5

Следовательно, данная линия является центральной. Координаты центра линии определим из системы уравнений (1.5), которая в дан-

ном случае имеет вид

5x0 4 y0 9 0;

4x0 5y0 9 0.

Решая эту систему, найдем x0 1, y0 1. Перенесем начало координат в точку O (1; 1) , сохраняя направление осей координат. Уравнение данной линии относительно новой системы координат O x y имеет

вид 5(x )2 8x y 5( y )2 a	0 .
33

Напомним, что при параллельном переносе системы координат в центр линии старшие коэффициенты в уравнении линии остаются без изменения, члены первой степени исчезают, а свободный член вычисляется подстановкой в левую часть исходного уравнения координат

центра	вместо текущих	координат:	a33	5 12	8 1 1 5 12 18 1
18 1	9 9 . Следовательно, окончательно уравнение данной линии
примет вид
	5(x )2	8x y 5( y )2	9	0 .	(1.13)

Далее сделаем поворот системы координат на угол , тангенс которого вычислим по формуле (1.11). В нашем случае

9