алгоритмы / MODELIR2

Моделирование 61

Моделирование случайного события

Например: если известна вероятность выпуска бракованных изделий P_б = 0.1, то смоделировать частоту выпадения этого события можно, разыграв равномерно распределенное случайное число из диапазона от 0 до 1 и установив, в какой из двух интервалов (от 0 до 0.1 или от 0.1 до 1) оно попало. Если число попадает в диапазон (0;0.1), то выпущен брак, то есть событие произошло, иначе - событие не произошло. При значительном числе экспериментов частота попадания чисел в интервал от 0 до 0.1 будет приближаться к вероятности P=0.1, а частота попадания чисел в интервал от 0.1 до 1 будет приближаться к P=0.9.

Фрагмент алгоритма.

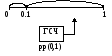
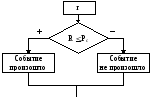
Моделирование полной группы несовместных событий

События называются несовместными, если вероятность появления этих событий одновременно равна 0. Отсюда следует, что суммарная вероятность группы несовместных событий равна 1.

a₁, a₂, ..., a_n - события

P₁, P₂, ..., P_n - вероятности появления отдельных событий

Так как события несовместны, то P_i = 1

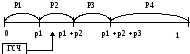
Алгоритм

Моделирование случайной величины с заданным законом распределения

1. Метод ступенчатой аппроксимации

Необходимо равномерный ГСЧ превратить в датчик с заданным законом распределения. Для этого непрерывный закон распределения вероятности события дискретизируем. h_i - высота i-ого столбца, f(x) - распределение вероятности (показывает насколько вероятно некоторое событие). И переходим к вероятностям. Так как сумма вероятностей всех k событий равна 1, то далее пользуемся методом моделирования группы несовместных событий.

Фрагмент алгоритма

2. Метод усечения

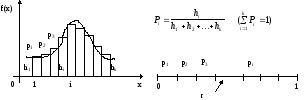
Используется в случае, когда функция задана аналитически (в виде формулы). Функцию заключают в прямоугольник. На ось Y подают случайное равномерно распределенное число из ГСЧ. На ось Х подают случайное равномерно распределенное число из ГСЧ. Если точка в пересечении этих двух координат лежит ниже кривой плотности вероятности, то событие X произошло, иначе нет.

Фрагмент алгоритма

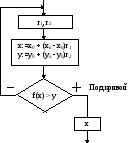
3. Метод взятия обратной функции

Допустим, задан 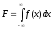- интегральный закон распределения вероятности, где f(x) - функция плотности вероятности.

Тогда достаточно разыграть случайное число, равномерно распределенное в интервале от 0 до 1. Поскольку функция F тоже изменяется в данном интервале, то случайное событие можно определить взятием обратной функции по графику или аналитически.

Пример: примем экспоненциальный закон распределения вероятности случайных событий

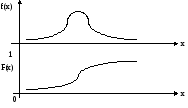
Заменяя F на случайное число r, имеем

В статическом смысле (1-r) и r - это одно и тоже, то есть

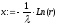
Фрагмент алгоритма.

Моделирование равномерно - распределенных случайных величин

1)

x:= a + b (b - a)  r (*)

разыгрываем случайное число.

2)

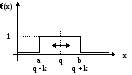
q - середина

x:= q  k, где k - отклонение от середины

x:= (q - k) + (q - k - q + k)  r = q + k  (2r - 1)

Моделирование нормально распределенных случайных величин

Нормальный закон распределения встречается в природе весьма часто, поэтому для него разработаны отдельные эффективные методы моделирования. Формула распределения вероятности по нормальному закону имеет вид:

,где m_x - математическое ожидание

_x - среднеквадратичное отклонение

Нормализованным нормальным распределением называется такое, у которого: _x=1 и m_x = 0.

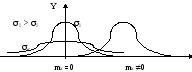
Функция нормального распределения имеет вид колокольчика (см. график)

(m_x  _x) - 68% точек

(m_x  2_x) - 95% точек

(m_x  3_x) - 99.7% точек

Чтобы получить нормальное число существуют следующие методы.

1. Табличный.

Для этого нормальное число можно взять из справочника в таблице функции Лапласа и получить случайное число по методу взятия обратной функции.

X	F
0,00	0,5
...	...
		r

F - интегральная функция Лапласа.

2) ЦПТ (используя центральную предельную теорему).

Теорема: “для большого числа случайных чисел с любым законом распределения, их сумма является случайным числом с нормальным законом распределения”. То есть требуется сложить случайные числа с любым законом их распределения, нормализовать их и перевести в нужный диапазон нормального распределения.

1. 

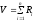
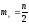
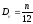
2. получение нормализованного нормального числа

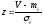m_z = 0 _z =1

где z - нормализованное число (m = 0, = 1)

3. получение нормального числа с заданными (m_x , _x )

x = z  _x + m_x

Отметим, что математическое ожидание смещает случайные числа, среднеквадратичное отклонение масштабирует закон распределения вероятности.

3). метод Муллера

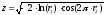
Пример: на склад поступают изделия партиями.

m_x = 35

_x= 10

Возьмем за основу генерации случайных чисел метод ЦПТ. После подстановки имеем

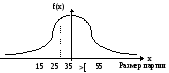
При количестве слагаемых n = 6 алгоритм генерации партий изделий примет вид

Моделирование марковских случайных процессов

Случайный процесс называется марковским (или процессом без последействия), если для каждого момента времени t, вероятность любого состояния системы в будущем зависит только от ее состояния в настоящем и не зависит от того, как система пришла в это состояние.

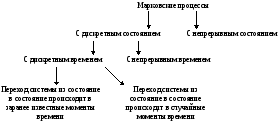
Марковские случайные процессы с дискретным временем

Марковская цепь

Если вероятность не зависит от времени, то марковскую цепь называют однородной.

Пример: Стрельба из пушки по цели. Выделим состояния:

S0 - цель не повреждена

S1 - цель повреждена

S2 - цель разрушена

Вектор начальных вероятностей:

	S0	S1	S2
P0 =	0.8	0.2	0

Матрица перехода состояний:

	S0	S1	S2
	0.45	0.4	0.15	S0
P=	0	0.45	0.55	S1
	0	0	1	S2

Определить среднее количество снарядов, необходимое для разрушения цели.

Построим марковскую цепь.

Заметим, что сумма вероятностей перехода из некоторого состояния всегда равна единице (куда-то система должна перейти обязательно). Алгоритм имитации будет иметь следующий вид.

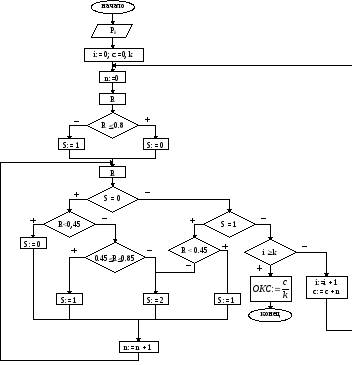
Марковские случайные процессы с непрерывным временем

Переход из одного состояния в другое происходит в случайные моменты времени, которые определяются _ij - интенсивностью перехода.

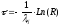- моменты совершения переходов

Пример: Станок может находиться в следующих состояниях:

S₀ - станок исправен, свободен (простой)

S₁ - станок исправен, занят (обработка)

S₂ - станок исправен, замена инструмента (переналадка) ₀₂ < ₂₁

S₃ - станок неисправен, идет ремонт ₁₃ < ₃₀

_{Нач.состояние}

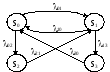
₀₁ - поток на обработку (без переналадки)

₁₀ - поток обслуживания

₁₃ - поток отказов оборудования

₃₀ - поток восстановлений

Фиксация и обработка статистических результатов

1. Вычисление средних величин может быть организовано несколькими способами.

1. Всю статистику вычисляют в конце.

- математическое ожидание

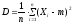- дисперсия

2. Всю статистику вычисляют в процессе вычисления (по рекурсивным соотношениям)

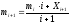
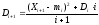
Всю статистику вычисляют в классовых интервалах (это самый лучший метод, он содержит универсальность 1-го и экономичность 2-го методов). Определяем в какой интервал попадает некая величина X и сколько раз.

2. Вычисление геометрии распределения необходимо для того, чтобы представить себе более точно характер распределения:

1-ый момент: 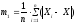- среднее арифметическое

2-ой момент: - дисперсия

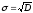- среднеквадратичное отклонение (характеризует разброс)

3-ий момент: 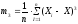- скошенность

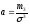
4-ый момент: - характеризует эксцесс (или остроплосковзвешенность). 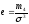- нормированный эксцесс

3. Оценка степени совпадения эмпирического закона распределения с теоретическим.

61