
А.В. Матисов Решение нелинейных уравнений
.pdfМинистерство образования Российской Федерации Государственное учреждение
Кузбасский государственный технический университет Кафедра информационных и автоматизированных производственных
систем
РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Методические указания к лабораторной работе по курсу "Информатика" для студентов специальности 210200 "Автоматизация технологических процессов и производств (в машиностроении)", 071900 "Информационные системы и технологии", 120100 "Технология машиностроения", 120200 "Металлорежущие станки и инструменты", 120500 "Оборудование и технология сварочного производства"
Составители А.В.Матисов Г.А.Алексеева В.И.Штефан
Утверждены на заседании кафедры Протокол № 3 от 05.11.02
Рекомендованы к печати учебно-методической комиссией по специальности 210200 Протокол № 78 от 20.11.02
Электронная копия находится в библиотеке главного корпуса ГУ КузГТУ
Кемерово 2003
1
1. ЦЕЛЬ РАБОТЫ
Целью работы является изучение численных методов решения нелинейных уравнений и получение практических навыков алгоритмизации задачи нахождения корней нелинейных уравнений.
2.ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
2.1.Основные положения
Все математические функции и уравнения, их содержащие, по виду можно разделить на линейные и нелинейные. К линейным относятся уравнения вида kx+b=0, в которые переменная (или аргумент) входит в первой степени.
Нелинейными называется уравнение вида
f(x) = 0, |
(2.1) |
где f(x) – алгебраическая или трансцендентная функция аргумента x, определенная на интервале [a, b]. Всякое x [a, b], при котором функция обращается в нуль, называется корнем уравнения (2.1).
Уравнение (2.1) называется алгебраическим, если его левая часть имеет вид многочлена
( an x n ) +( an−1 x n−1 ) +K+( a1 x ) +a0 = 0 , |
(2.2) |
где n ≥ 2.
Уравнение (2.2) имеет n действительных или комплексных корней. В курсе математики изучаются линейные и квадратные уравнения, корни которых могут быть найдены по известным формулам. Существуют также формулы для решения уравнений 3-й и 4-й степеней, однако они очень сложны и неудобны для практического применения. Для уравнений 5-й и более высоких степеней норвежским математиком Н. Абелем в 20-х годах XIX века доказано, что решение таких уравне-
ний нельзя выразить более точными формулами.
Если левая часть уравнения (2.1) является неалгебраической функцией, например логарифмической, показательной, тригонометри-
2
ческой, бесселевой и т.д., то уравнение (2.1) называется трансцендентным и может иметь как конечное, так и бесконечное число корней или не иметь их вообще. В случае трансцендентной функции найти явные выражения для корней уравнения (2.1) за редким исключением не удается.
Решение уравнения (2.1) сводится к отысканию приближенных значений корней, т.е. к нахождению численных величин, которые с заданной точностью обращают f(x) в нуль. При этом приходится решать две задачи: задачу отделения корней уравнения и задачу вычисления корней с заданной точностью.
2.2. Отделение корней нелинейного уравнения
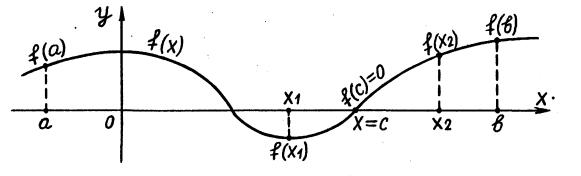
Пусть f(x) есть нелинейная функция, определенная и непрерывная на некотором интервале [a, b]. Предполагается (рис. 2.1), что внутри интервала [a, b] существует такой интервал [x1, x2], на котором функция f(x) непрерывна и меняет знак, т.е. f(x1) f(x2) < 0, а ее производная f ′(x) знак сохраняет.
Если функция f(x) непрерывна на отрезке [х1, х2] и принимает на его концах значения разных знаков, то на этом отрезке существует хотя бы один корень уравнения (2.1). Если при этом производная f '(x) на данном отрезке знак не меняет, то на отрезке [х1, х2] находится только один корень уравнения f(x)=0. Интервал [х1, х2], удовлетворяющий указанным условиям, называется интервалом изоляции (или локализации) корня (рис. 2.1).
Рис. 2.1. График нелинейной функции
3
Итак, задача отделения корней сводится к отысканию таких областей, в каждой из которых заключен один и только один корень уравнения (т.е. к определению интервалов изоляции).
Рассмотрим некоторые способы определения областей, в которых расположены все корни уравнения, и способы отделения корней. Все корни алгебраического уравнения (2.2) расположены в интервале
|
a0 |
|
|
|
|
≤ |
|
x |
|
≤ 1 + |
|
|
a |
|
|
, |
(2.3) |
||
|
|
|
|
|
|
|
|||||||||||||
|
|
||||||||||||||||||
a′+ |
|
a0 |
|
|
|
|
an |
|
|
||||||||||
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где a = max{|an-1|, |an-2|, …, |a0|}, a' = max{|an|, |an-1|, …, |a1|}, a0, a1, …, an – коэффициенты многочлена.
Этот способ удобно применять тогда, когда допустима грубая оценка границ расположения корней.
В общем случае отделение корней уравнения (2.1) проводят по следующей схеме: анализируют вид функции f(x), вычисляют значения функции в некоторых (характерных) точках, по графику функции определяют интервалы изоляции корней.
При отделении корней полезно помнить следующие утверждения:
a)если непрерывная функция f(x) принимает значения разных знаков на концах промежутка [а, b], то внутри этого отрезка содержится по меньшей мере один корень уравнения f(x)=0;
b)если при этом первая производная f '(x) сохраняет знак на отрезке [а, b], то на отрезке [а, b] будет расположен единственный корень уравнения f(x)=0;
c)для отделения корней можно использовать и такой способ: функцию f(x) представляют в виде разности двух функций: f(x)=v(x)- w(x), причем v(x) и w(x) подбирают так, чтобы графики у=v(х) и y=w(x) можно было легко построить; корни уравнения f(x)=0 будут абсциссами точек пересечения этих графиков; чтобы отделить корни исходного уравнения, достаточно довольно приближенно найти интервалы, где расположены абсциссы точек пересечения графиков y=v(x) и y=w(x).
Возьмем в качестве примера простое уравнение: x-cos(x)=0.
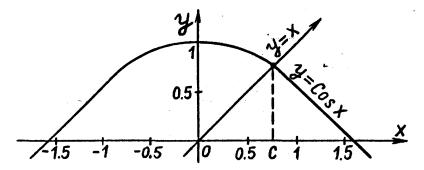
Это уравнение можно представить как разность двух элементарных функций у=х и y=cosx. Перепишем исходное уравнение в виде x=cosx и построим графики функций, стоящих в левой и правой части. Как видно из рис. 2.2, они пересекаются при х=с (0<с<1). Число с явля-
4
ется корнем, однако получить для него формулу невозможно. Проанализируйте функцию на интервале [0, 1], содержащем корень х=с.
Рис. 2.2. Графическое решение уравнения x-cosx=0
Функция f(x)=x-cosx непрерывна на отрезке [0, 1], а ее значения на концах отрезка имеют разные знаки: f(0)=0-cos(0)=-1<0 и f(1)=1-cos(1)=0,47>0.
Отсюда сразу следует существование на отрезке [0, 1] по крайней мере одного корня. Проведем дополнительное исследование: вычислим производную функции f '(x)=(x-cosx)'=1+sinx.
В интересующем нас интервале [0, 1] производная положительна (знак не меняет). Следовательно, функция f(x) на отрезке [0, 1] монотонно возрастает и может иметь только один корень (х=с).
Ознакомившись с методом предварительного качественного исследования уравнений, перейдем к задаче вычисления (уточнения) корней с заданной точностью.
2.3. Вычисление корней с заданной точностью
На этом этапе производится уточнение корней с помощью численных методов для достижения заданной степени точности корней уравнения. Чаще всего используют итерационные численные методы. Окончание вычисления корня итерационным методом определяется принятым заранее критерием.
5
2.3.1. Метод половинного деления
Метод является одним из наиболее простых итерационных методов вычисления вещественного корня уравнения f(x)=0.
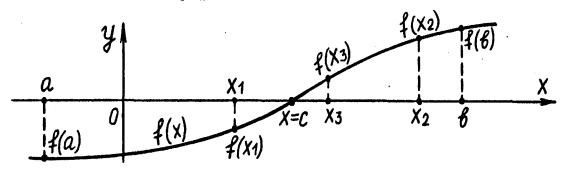
Рассмотрим нелинейную функцию f(x) (рис. 2.3), определенную и непрерывную в интервале [а, b]. На этапе отделения корней получен интервал изоляции корня [x1, х2]. В точках х1 и х2 функция имеет противоположный знак, т.е. f(x1) ×f(х2)<0. Это означает, что где-то внутри интервала функция пересекает ось абсцисс.
Рис. 2.3. Графическая интерпретация метода половинного деления
Метод заключается в следующем:
1.Выбираем (для окончания вычислений) точность вычисления корня Е. Вычисления можно прекратить, когда интервал, содержащий корень, станет меньше Е. Необходимо помнить, что уменьшение Е дает более точный результат, но приводит к увеличению процесса и времени вычислений. Поэтому ограничиваются практически необходимой для конкретной задачи точностью.
2.Устанавливаем границы интервала изоляции корня х1 и х2.
3.Вычисляем F1=f(x1) и F2=f(x2).
4.Если F1×F2>0, то [х1, х2] не интервал изоляции. Идти к пункту 2.
5.Вычисляем х3=(x1+x2)/2 (т.е. берем точку х3 на середине интер-
вала [х1, х2]).
6.Вычисляем F3=f(х3).
7.Если F3=0, то х1=х3 и х2=х3. Идти к пункту 10.
8.Если F1×F3<0, то полуинтервал [х1, х2] содержит корень, присваиваем х2=х3, перейти к пункту 10.

6
9.Присваиваем х1=х3 и F1=F3 (т.е. полуинтервал [х3, х2] содержит
корень).
10.Если |x1-x2|≥Е, то идти к пункту 5.
11.Искомый корень равен хЗ и функция F3=f(x3).
Метод сходится для любых непрерывных функций, в том числе для не дифференцируемых. Итерационный процесс (пункты 5-10) приводит к тому, что после n итераций длина интервала, содержащего корень, становится меньше первоначальной в 2n раз и равной хn=(х2-х1)/2n. Следовательно, для выполнения условия |xn |<E требуется число итераций:
N = ln(( x2 − x1 ) E ) ln 2. |
(2.4) |
Это означает, что для получения каждых трех верных десятичных знаков необходимо совершить около 10 итераций.
2.3.2.Метод простых итераций
Метод называется итерационным, если решение с его помощью может быть получено как результат процесса повторяющихся операций, при котором каждая следующая операция уточняет значения неизвестных, используя приближенные значения, уже найденные на предыдущих операциях.
Итерационные методы не всегда сходятся, однако если они сходятся, то затраты времени на получение решения (с требуемой точностью) сокращаются по сравнению с точными методами решения этой же задачи. Итерационные методы, в отличие от точных, требуют предварительной проверки условий сводимости и выбора начального приближения.
Метод простых итераций заключается в следующем. Исходное уравнение f(x)=0 преобразуется к виду x=v(x). Выбрав начальное приближение корня х0, принадлежащее интервалу изоляции, и подставив его в правую часть преобразованного уравнения, вычислим уточненное значение x1=v(x0). Затем вычислим х2=v(x1), ..., xn=v(xn-1). Предел последовательности х0, x1, x2, …, xn, если он существует, является искомым корнем х уравнения f(x)=0.
Условием сходимости процесса итераций, т.е. условием существования указанного предела, является выполнение неравенств |v'(x)|<1 в
7
интервале изоляции. Сходимость будет тем более быстрой, чем меньше величина |v'(x)|.
Рассмотрим применения метода на конкретном примере. Возьмем знакомое уже нам уравнение f(x)=x-cosx=0. Преобразуем его к виду x=cosx и исследуем правую часть на сходимость. | v'(x)| = |-sinx| <1, следовательно, в интервале [0, 1] процесс итераций сходится (рис. 2.2).
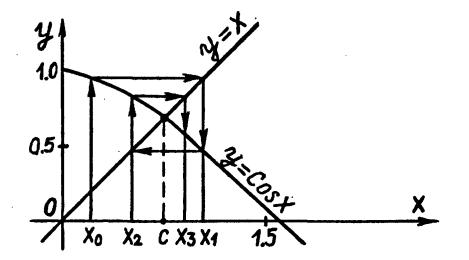
Рис. 2.4. Графическая интерпретация метода простых итераций
Рассмотрим теперь алгоритм уточнения корня.
1.Выберем точность вычислений корня Е.
2.Возьмем начальное приближение x0 [0, 1] (рис.2.4).
3.Вычислим x=cos(x0).
4.Если |х-х0 |≥Е, то х0=х. Идти к пункту 3.
5.Искомый корень равен х и функция F=cos(x). Итерационный процесс (пункты 3-4) отражен на рис.2.4.
Приведем два способа преобразования уравнения (2.1) к виду
x=v(x).
1. Переход к обратной функции. Если после первоначального преобразования функция v(x) удовлетворяет неравенству |v'(х)|>1,то можно от функции y=v(x) перейти к обратной функции x=w(y), для которой будет выполняться неравенство:
(1/|w'(x)|)<1. |
(2.5) |
8
Метод итераций в применении к уравнению y=w(y) будет сходиться. При этом корень уравнения у=w(у) будет являться корнем уравне-
ния x=w(x).
2. Подбор множителя. Уравнение (2.1) будет равносильно уравне-
нию
x = x - g(x) f(x), |
(2.6) |
если v(x) не равна 0 и непрерывна на интервале изоляции. Для сходимости метода функцию g(x) достаточно подобрать так, чтобы в окрестности корня выполнялось условие
|( x = g(x) f(x) )' |<1. |
(2.7) |
Например, если известны нижняя m и верхняя М границы производной функции f(x), так что 0<m≤ f '(x)≤ M, то в качестве g(x) можно взять величину 2/(m+М). Тогда для уравнения
x = x - f(x) 2 / (m+M) |
(2.8) |
метод итераций сходится.
2.3.3.Метод касательных (метод Ньютона)
Метод касательных является одним из наиболее эффективных. Идея его очень проста. Предположим, что функция f(x) на определенном ранее интервале изоляции [х1, х2] дифференцируема, а ее производные f '(x) и f ''(х) непрерывны и не обращаются в нуль на [х1, х2] (сохраняют определенные знаки). За начальное приближение х0 [х1, х2] принимают любую точку, в которой знаки f(x) и f ''(x) совпадают, т.е. чтобы выполнялось неравенство f(x) f ''(х) >0. Запишем уравнение касательной к графику функции f(x) в точке х0.
y = f (x0) + f '(x0) (x-x0). |
(2.9) |
Графики функций f(x) и ее касательной близки около точки касания (рис. 2.5), поэтому точка х пересечения касательной с осью абсцисс
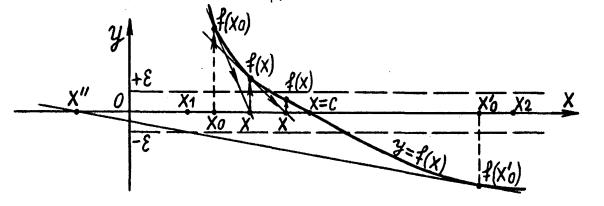
9
будет расположена недалеко от корня x=с. Для определения этой точки х имеем уравнение f(x0)+f '(x0) (x-x0)=0, откуда
x = x0 – f (x0) / f '(x0). |
(2.10) |
Каждое следующее приближение вычисляется по рекуррентной формуле
xn+1 = xn – f (xn) / f '(xn), |
(2.11) |
где n = 0, 1, 2, ….
Вычисления можно прекратить, когда модуль функции f(x) при очередном приближении x будет меньше точности корня Е.
Рис. 2.5. Графическая иллюстрация метода касательных
Если за начальное приближение принять точку (х'), в которой знаки f(х') и f ''(х') противоположны, то в результате вычислений получим точку (х''), которая не является приближением к корню и даже выходит за интервал изоляции (рис. 2.5).
1.Выберем точность вычислений корня Е.
2.Установим границы интервала изоляции x1 и х2.
3.Возьмем начальное приближение х0, принадлежащее [x1, x2].
4.Вычислим F=f(x0) и F2=f ''(x0).
5.Если F× F2<0, то идти к пункту 3.
6.Присвоим x=x0.
7.Вычислим х=x-f(x)/f '(x).
8.Вычислим y=f(x).
9.Если |у|≥Е, то идти к пункту 7.
