
М.А. Тынкевич Потоки в сетях и транспортная задача по критерию времени
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
КУЗБАССКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра вычислительной техники и информационных технологий
ПОТОКИ В СЕТЯХ И ТРАНСПОРТНАЯ ЗАДАЧА ПО КРИТЕРИЮ ВРЕМЕНИ
Методические указания и задания к практическим занятиям по курсам
“Исследование операций в экономике” и “Экономико-математические методы”
для студентов экономических специальностей
Составитель М.А.Тынкевич
Утверждены на заседании кафедры вычислительной техники и информационных технологий Протокол № 4 от 08.12.2000
Рекомендованы к печати методической комиссией по специальности 351400
Протокол № 1 от 08. 12.2000
Кемерово 2001
1
1. Задача о максимальном потоке
Рассмотрим транспортную сеть, в которой выделены пункты 0 (вход, источник) и n (выход, сток) и каждой дуге (отрезку), связывающей пункты
i и j, сопоставлено число dij > 0 , называемое пропускной способностью дуги. Величина пропускной способности характеризует максимальное допустимое количество вещества (воды, газа, самолетов, вагонов и т. п.), которое может проходить по соответствующей дуге в единицу времени.
Количество вещества, проходящего по дуге от i до j в реальности, будем называть потоком по дуге ( i , j ) и обозначать через Xij .
Очевидно, что |
|
|
|
0 ≤ |
Xij ≤ |
dij для всех i , j . |
|
Если учесть, что все вещество, |
вошедшее в промежуточный пункт сети, |
||
должно полностью выйти из него, |
получаем |
||
∑ |
X i j = ∑ |
X jk , j = 1 ..n . |
|
i |
|
k |
|
Для стационарных потоков, параметры которых в любой момент времени неизменны, естественно требовать равенства потоков на входе и на выходе :
∑ X 0 j = ∑ X i n = Z .
j i
Рассмотрим задачу максимизации величины потока в сети Z при указанных условиях .
Подобная задача возникает достаточно часто. Под каким давлением подавать воду в городскую сеть, чтобы не рвались (или хотя бы меньше рвались) трубы? Какое количество газа можно качать от месторождений Ямала к потребителям в Европе?
Решение задачи можно осуществлять методами линейного программирования, но едва ли эта возможность осуществима для сколь-нибудь реальной сети.
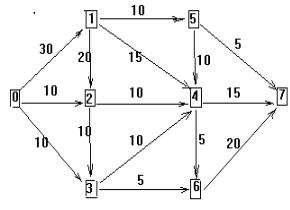
В случае т. н. (0, n) - плоских сетей, т. е. сетей, которые можно изобразить на плоскости по одну сторону от ли-
нии, соединяющей вершины 0 и n , без пересечения дуг вне вершин (наша сеть относится к таковым), можно предложить простой наглядный алгоритм решения.
Берем самый "верхний" (по принципу левостороннего движения) путь от вершины 0 к вершине 7: [0 - 1 - 5 - 7] и отыскиваем минимальную пропускную способность составляющих его дуг, равную 5 , и уменьшаем пропускные

2
способности дуг на эту величину. Очередной "верхний" путь [0 - 1 - 5
- 4 - 7] имеет пропускную способность 5.
Очередной путь [0 - 1 - 4 - 7] имеет пропускную способность 10. Последующий поиск обнаруживает потоки по путям [0 - 1 - 4 - 6 - 7] c величиной потока 5 и [0 - 1 - 2 - 3 - 6 - 7] c величиной 5 . В итоге сеть ока-
залась разорванной и максимальный поток равен 30 .
Естественно, что для больших сетей такой метод неприемлем. К тому же он не слишком удобен для компьютерной реализации.
Рассмотрим матричную реализацию алгоритма поиска в произвольной сети. Начальный этап алгоритма состоит в построении матрицы D0 , в которую заносятся значения пропускных способностей (для неориентированной дуги
берем симметричные значения элементов матрицы di j=dj i ).
Основные шаги алгоритма состоят в поиске некоторого пути и коррекции потока на этом пути.
При поиске пути используем процесс отмечаний.
Метим символом * нулевые строку |
и столбец матрицы (вход сети). В |
|
нулевой строке отыскиваем d0j |
> 0 и |
метим соответствующие столбцы ин- |
дексами |
|
|
|
j = 0 , |
V j = d0j |
и переносим метки столбцов на строки. |
Затем берем i-ю отмеченную стро- |
|
ку, ищем в ней непомеченный столбец с d i j > 0 и сопоставляем ему метки
j = i , Vj = min (Vj, di j).
Метки столбцов переносим на строки и этот процесс продолжаем до тех
пор, пока не будет отмечен n - й столбец. |
выясняем путь, приведший к n - |
Затем "обратным ходом" по индексам |
й вершине, и уменьшаем пропускные способности дуг пути (элементы мат-
рицы) на Vn и увеличиваем симметричные элементы на эту же величину. Такая процедура продолжается до тех пор, пока отмечание n - й вершины
не станет невозможным.
Максимальный поток может быть найден суммированием найденных промежуточных потоков или вычитанием из исходной матрицы D0 получаемой после вышеприведенной корректуры матрицы пропускных способностей
X = max (D0 - Dk , 0) .
Обратимся к рассмотренному выше примеру.
Из нулевой строки отмечаем вершины (строки-столбцы) 1 , 2 и 3 индексами =0 и V, равными 30 , 10 и 10.
Из помеченной строки 1 метим вершины 4 и 5 индексами =1 и
V4 = min( 30, 15 ) = 15 , V5 = min( 30,10 ) = 10 .
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
Из строки 3 |
метим вершину 6 |
и, наконец, |
из строки 4 |
- вершину 7. |
||||||||||||||||
|
|
* |
|
0/30 |
0/10 |
0/10 |
1/15 |
1/10 |
3/5 |
4/15 |
|
|
||||||||
|
|
|
0 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
* |
|
||||||
|
0 |
|
|
|
|
30 |
|
10 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
20 |
|
|
15 |
|
10 |
|
|
|
|
|
0/30 |
|
D0 = |
2 |
|
|
|
|
|
|
|
10 |
|
10 |
|
|
|
|
|
|
|
0/10 |
|
3 |
|
|
|
|
|
|
|
|
10 |
|
|
5 |
|
|
|
0/10 |
||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
15 |
|
1/15 |
||
|
5 |
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
5 |
|
1/10 |
||
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
3/5 |
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4/15 |
|
Обратным |
ходом по |
обнаруживаем путь: к вершине 7 от 4 , |
к верши- |
|||||||||||||||||
не 4 от 1 , к |
вершине 1 от 0; корректируем элементы |
|
D0 |
на |
величину |
|||||||||||||||
потока V7 =15. На очередном шаге находим путь [ 0 - 1 - 5 - 7 ] |
с потоком 5 . |
|||||||||||||||||||
|
|
* |
|
0/15 |
0/10 |
0/10 |
2/10 |
1/10 |
3/5 |
5/5 |
|
|
|
|||||||
|
|
|
0 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
* |
|
||||||
|
0 |
|
|
|
|
15 |
|
10 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
15 |
|
|
|
20 |
|
0 |
|
10 |
|
|
|
|
|
0/15 |
|||
D1 = |
2 |
|
|
|
|
|
|
|
10 |
10 |
|
|
|
|
|
|
|
0/10 |
||
3 |
|
|
|
15 |
|
|
|
10 |
|
|
5 |
0 |
|
0/10 |
||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
5 |
|
2/10 |
||||||
|
5 |
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
5 |
|
1/10 |
||
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
3/5 |
|
|
7 |
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
5/5 |
с пото- |
|
Последующие шаги обнаруживают пути [0-3-6-7] и [0-2-4-6-7] |
||||||||||||||||||||
ками величиной 5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
* |
|
0/10 |
0/5 |
0/5 |
2/5 |
1/5 |
|
|
|
|
|
|
|
|||||
|
|
|
0 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
* |
|
||||||
|
0 |
|
|
|
10 |
5 |
5 |
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
20 |
|
|
20 |
|
0 |
5 |
|
|
|
|
|
0/10 |
|||||
D4 = |
2 |
|
5 |
|
|
|
|
10 |
5 |
|
|
|
|
|
|
|
0/10 |
|||
3 |
|
5 |
15 |
5 |
|
10 |
|
|
0 |
0 |
|
0/5 |
|
|||||||
|
4 |
|
|
|
|
|
|
|
|
0 |
|
2/5 |
|
|||||||
|
5 |
|
5 |
|
|
|
|
|
10 |
|
|
|
|
0 |
|
1/5 |
|
|||
|
6 |
|
|
|
|
|
|
|
5 |
5 |
|
|
|
|
10 |
|
|
|
||
Дальнейшее |
7 |
|
|
|
|
|
|
|
|
15 |
5 |
10 |
|
|
|
|
|
|||
|
отмечание невозможно. |
Отсюда получаем матрицу макси- |
||||||||||||||||||
мального потока: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
0 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
|||||
|
|
|
0 |
|
|
|
20 |
5 |
5 |
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
|
|
|
|
0 |
|
|
15 |
5 |
|
|
|
|
|
||
|
|
|
2 |
|
|
|
|
|
|
0 |
5 |
|
|
|
|
|
|
|
||
Xmax = |
3 |
|
|
|
|
|
|
|
|
0 |
|
|
5 |
15 |
|
|||||
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|||
|
|
|
5 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
5 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4
Этот алгоритм не накладывает никаких ограничений на транспортную сеть типа наличия ориентации или возможности размещения на плоскости без пересечения дуг, элементарно реализуется в программном виде; им можно пользоваться и при ручном поиске (разумеется, не перерисовывая таблицы, а пользуясь карандашом и резинкой) .
2. Транспортная задача по критерию времени
В отличие от традиционной транспортной задачи |
в рассматриваемой |
кри- |
|||||
терием |
качества организации перевозок являются |
не суммарные затраты, а |
|||||
время |
реализации перевозок (подобные проблемы |
возникают при транспор- |
|||||
тировке скоропортящихся грузов, при переброске |
сил быстрого реагирова- |
||||||
ния и т.д.). |
m |
|
|
в количествах ai (i=1…m) и n |
|||
Пусть имеется |
поставщиков |
продукта |
|||||
потребителей в |
количествах bj ( |
j = 1... n ) , |
причем соблюдается |
баланс |
|||
предложения и спроса. |
|
|
|
|
|||
Известно время ti |
j прямой поставки груза |
от i |
- го поставщика к |
j - му |
|||
потребителю, не зависящее от объема перевозки. |
|
|
|||||
Требуется среди всех допустимых планов |
перевозок X = { Xij } |
найти |
|||||
план, оптимальный |
по времени. Очевидно, что время, необходимое для реа- |
||||||
лизации плана, совпадает с наибольшим временем отдельных перевозок и оптимальное время перевозок равно
Topt |
= min |
max t |
i j |
(1) |
|||
|
|
|
|
X |
Xi j > 0 |
|
|
при условиях |
|
|
|
|
|
|
|
∑n |
X i |
j = ai |
, |
i = 1 .. m; |
(2) |
||
j= 1 |
|
|
|
|
|
|
|
∑m |
X i j = b j |
, |
j = 1 .. n; |
(3) |
|||
i= 1 |
|
|
|
|
|
|
|
Xi j ≥ |
0 |
|
, |
i = 1 .. m , j = 1 .. n; |
(4) |
||
∑m |
ai = ∑n |
b j = |
R . |
|
(5) |
||
i= 1 |
|
j=1 |
|
|
|
|
|
|
|
|
|
|
|
|
b1 |
|
|
a1 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b2 |
|
|||
|
|
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||
am |
|
|
|
|
|
||||
|
|
|
bn |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
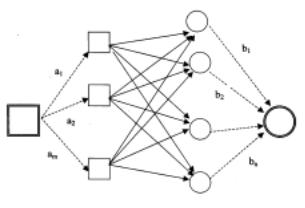
Для решения поставленной задачи воспользуемся весьма простой идеей.
Считая пропускные способности маршрутов транспортной сети скольугодно большими, построим вспомогательную сеть, дополнив исходную псевдовходом, из которого ведут дуги к поставщикам с пропускными способно-
стями ai (i = 1…m), и псевдовыхо-
дом, к которому ведут дуги от по-
5
требителей с пропускными способностями bj (j=1…n). В результате получаем сеть с одним входом и одним выходом, в которой осуществляется переброска R единиц груза от псевдовхода до псевдовыхода.
Выбираем минимальное из значений tij и строим т.н. допустимую сеть,
удаляя дуги со значениями tij , превышающими выбранное. В этой сети отыскиваем максимальный поток (алгоритм такого поиска рассмотрен выше). Если этот поток отвечает условиям задачи (его величина равна R), то выбранное время оптимально. В противном случае выбирается очередное наименьшее время, тем самым допустимая сеть расширяется и в ней вновь ищется максимальный поток.
Единственный недостаток такого решения в том, что придется оперировать с матрицами размерности m+n+2, в которой всего mn+m+n ненулевых элементов. Поэтому рассмотрим компактную схему поиска максимального потока, позволяющую работать с матрицами размерности m× n.
Пусть найден некоторый поток X в допустимой сети S, удовлетворяющий естественным условиям:
∑n |
X i j ≤ ai ( i = 1 .. m ) ; |
∑m |
X i j ≤ b j ( j = 1 .. n ) ; X i j ≥ 0 (i=1..m , j=1..n). |
j= |
1 |
i= 1 |
|
(поиск начального приближения для потока можно осуществлять любым методом, например, методом северо-западного угла).
Для строк i, в которых
|
|
|
|
∑n |
X i |
j |
< ai |
, |
|
|
|
|
(6) |
|
|
|
|
j= 1 |
|
|
|
|
|
|
|
|
|
сопоставим метки |
|
|
|
|
i = ai - ∑n |
|
|
|
|
|
|||
|
µ |
i = 0 |
, |
υ |
X i j . |
|
|
(7) |
|||||
|
|
|
|
|
|
|
|
j= 1 |
|
|
|
|
|
Выбираем отмеченные |
строки (например, |
i -ю) и отмечаем неотмеченные |
|||||||||||
столбцы j такие, что дуга (i j) |
S , |
метками |
|
|
|
|
|
|
|||||
|
|
λ j = i |
, |
ω |
j = |
υ i . |
|
|
|
(8) |
|||
Затем берем отмеченные столбцы (например, |
j - й) и |
неотмеченным |
|||||||||||
строкам i , в которых X i j |
> 0 , сопоставляем метки |
|
|
|
|
||||||||
|
|
µ i = |
j |
, υ |
i = |
|
min (ω |
j , Xi j |
) . |
|
(9) |
||
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
Повторяем процесс отмечания столбцов и строк до тех пор, |
пока |
не будет |
|||||||||||
отмечен "ненасыщенный" столбец j* , |
для которого |
|
|
|
|
||||||||
|
|
|
∑m X |
* |
< |
b * |
|
|
|
|
(10) |
||
|
|
|
i= |
1 |
i j |
|
j . |
|
|
|
|
||
Отыскиваем величину |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
∑m X |
|
|
|
|
|
|
Θ |
= min ( ω * |
,b * − |
i |
* ) |
, |
(11) |
||||||
|
|
|
|
|
j |
|
j |
|
i= 1 |
j |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
определяющую |
величину |
|
потока |
|
в найденном пути; |
поочередно добавляем |
||||||||||||||||||||||||||
и вычитаем Θ |
из значений X i j в цепочке |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
( |
i |
0 |
j* ) ( i |
0 |
j |
1 |
) ( i |
1 |
j |
1 |
) ( i |
1 |
j |
2 |
) ( i |
2 |
j |
2 |
) ...( i |
k-1 |
j |
k |
) ( i |
k |
j |
k |
) |
|||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
= |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 0 ) |
||
i0 |
= l * , j1 |
mi |
|
,i1 |
l j |
1 |
, j2 |
= mi |
, i2 |
= l j ,.. ,ik |
= l j |
k |
(mi |
|
||||||||||||||||||
|
|
|
j |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
k |
|
|
||||
и вновь продолжаем процесс отмечаний. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Если не удастся отметить |
ни одного из |
|
ненасыщенных столбцов, |
то пере- |
||||||||||||||||||||||||||||
страиваем сеть. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Очевидно, что для выбора начального времени разумнее отталкиваться не
от минимального из значений tij, а от максимального |
среди |
|
минимальных |
||||||||||||||||
времен в строках и столбцах матрицы T . |
|
|
|
|
|
|
|
|
|||||||||||
Пример1. Пусть задача определена следующими данными. |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Минимальные значения ti j в строках равны |
||||||||
T = |
1 |
|
13 |
|
17 |
18 |
18 |
|
1, 2, 1 и в столбцах 1 , 1 , 4 , 10. |
|
|
|
|||||||
2 |
|
18 |
|
10 |
10 |
10 |
|
Выбираем t*=10, строим вспомогательную |
|||||||||||
|
16 |
|
1 |
|
4 |
12 |
12 |
|
сеть по tij ≤ |
t* и отыскиваем в ней начальное |
|||||||||
|
11 |
|
9 |
|
13 |
7 |
B\A |
|
|||||||||||
|
|
|
|
приближение для потока методом северо- |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
западного угла. |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как |
найденный поток |
X |
не является |
|||||
|
|
11 |
|
|
|
|
|
18 |
|
|
|||||||||
o |
|
0 |
|
|
|
|
10 |
0 |
10 |
|
насыщающим, пытаемся |
его |
улучшить с ис- |
||||||
X = |
|
|
|
|
|
|
пользованием процесса |
отмечаний |
|
||||||||||
|
|
|
|
9 |
|
3 |
|
12 |
|
|
|||||||||
|
|
|
|
|
|
|
µ 1 = 0, υ 1 = 18 - 11 = 7; |
λ |
1 =1, ω 1 = υ 1 = 7. |
||||||||||
|
|
11 |
|
9 |
|
13 |
7 |
B\A |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
Дальнейшее |
отмечание |
невозможно |
и |
|||||
приходится расширить сеть, |
|
взяв t*=12 (появится возможность перевозки на |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
маршруте 1 – 4 , поток Xo′). |
|
|
|
|
|
|||
|
11 |
|
|
|
|
|
|
18 |
|
Очевидно, что это расширение ничего ново- |
|||||||||
Xo′= |
0 |
|
|
|
10 |
0 |
10 |
|
го не даст; берем t*=13 , поток |
X |
|
′′). |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
o |
|
|
|
|
|
|
|
9 |
|
3 |
0 |
12 |
|
Отталкиваясь от ранее выбранного потока, |
|||||||||
|
11 |
|
9 |
|
13 |
7 |
B\A |
|
пытаемся его улучшить. |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Продолжая процесс отмечаний, имеем |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
λ 2 = 1 , ω 2 = υ 1 = 7 ; |
|
||||||
|
11 |
|
0 |
|
|
|
|
18 |
|
|
|
||||||||
|
|
|
|
|
|
µ 3 |
= 2 , |
υ 3 = min(X3 2 , ω 2) = 7 ; |
|
||||||||||
Xo′′= |
0 |
|
|
|
10 |
0 |
10 |
|
|||||||||||
|
|
|
|
|
λ 2 = 3 , ω 4 = υ 3 = 7 . |
|
|||||||||||||
|
|
|
|
9 3 |
0 |
12 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
Так как |
отмечен ненасыщенный столбец, |
|||||||
|
11 |
|
9 |
|
13 |
7 |
B\A |
|
|||||||||||
|
|
|
|
отыскиваем |
цепочку [ X34 |
X32 |
|
X12 ] и |
кор- |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
ректируем ее на |
величину |
Θ |
= min (ω 4 |
,B4 ) |
||||
|
11 |
|
7 |
|
|
|
|
18 |
= 7. |
|
|
|
|
|
|
|
|
||
X1 = |
0 |
|
2 |
|
10 |
0 |
10 |
|
В итоге |
мы |
получаем |
насыщающий |
по- |
||||||
|
|
|
|
|
3 |
7 |
12 |
|
ток и можем утверждать, что |
минимальное |
|||||||||
|
11 |
|
9 |
|
13 |
7 |
B\A |
|
время транспортировки составляет 13 единиц. |
||||||||||

7
Пример 2. Рассмотрим задачу с данными, приведенными в таблице. Минимальные значения ti j в строках
10 |
13 |
17 |
18 |
10 |
25 |
и столбцах |
равны 10. Соответственно |
||||
T = 12 |
18 |
10 |
10 |
10 |
35 |
выбираем t*=10, строим вспомога- |
|||||
16 |
10 |
14 |
12 |
11 |
15 |
тельную сеть |
и отыскиваем |
в ней на- |
|||
|
17 |
10 |
10 |
13 |
19 |
25 |
чальное приближение X0. |
X0 не |
|
||
|
20 |
20 |
13 |
7 |
40 |
B\A |
Так как найденный поток |
яв- |
|||
|
|
|
|
|
|
|
ляется |
насыщающим, пытаемся |
его |
||
улучшить |
с использованием процесса отмечаний |
|||||||
|
|
|
|
|
|
|
µ 4 = 0, |
υ 4= 25 - 5 = 20; |
Xo = |
20 |
|
|
|
5 |
25 |
||
|
|
|
13 7 |
15 |
35 |
λ 2 =4, ω 2 =υ 4 = 20; λ 3 =4, ω 3 =υ 4 = 20; |
||
|
|
|
15 |
|
|
15 |
µ 3 = 2, |
υ 3=min( 20,15) = 15; |
|
|
5 |
0 |
|
25 |
µ 2 = 3, |
υ 2=min( 20,13) = 13; |
|
|
20 |
20 |
13 |
7 40 |
B\A |
λ 5 =2, ω 5 =υ 2 = 13. |
||
|
|
|
|
|
|
|||
Поскольку отмечен ненасыщенный столбец 5, находим величину коррекции θ =min (ω 5 =13, 40-5-15)=13, строим
цепочку [X43 |
X23 |
X25 ] и поочередно увеличиваем и уменьшаем элементы це- |
||||||||
|
|
|
|
|
|
|
|
|
почки на θ , получая поток X1. |
|
|
20 |
|
|
|
|
|
5 |
25 |
||
X1 = |
|
|
|
|
|
Выполняя процесс отмечаний, имеем |
||||
|
|
|
|
0 |
7 |
28 |
35 |
|||
|
|
|
µ 4 = 0, |
υ 4= 25 – 5-13 = 7; |
||||||
|
|
|
15 |
|
|
|
|
15 |
||
|
|
|
|
|
|
|
λ 2 =4, ω 2 =υ |
4 = 7; λ 3 =4, ω 3 =υ 4 = 7; |
||
|
|
|
5 |
|
13 |
|
|
25 |
||
|
|
|
|
|
|
|
|
|
µ 3 = 2, |
υ 3=min( 7,15) = 7. |
|
20 |
|
20 |
|
13 |
7 |
40 |
B\A |
||
|
|
|
|
|
|
|
|
|
Дальнейшее отмечание невозможно и |
|
приходится расширить сеть, взяв t*=11 (появится возможность перевозки на
маршруте 3 – 5 , поток X2). |
|
|
|
|
Продолжая процесс отмечаний, начатый |
||||||||||||
X2 = |
20 |
|
|
|
0 |
7 |
5 |
|
25 |
|
выше, получаем возможность отметить |
||||||
|
|
|
|
28 |
|
35 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ненасыщенный столбец |
|
|
|||
|
|
|
|
15 |
|
|
|
0 |
|
15 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
λ 5 =3, ω |
5 =υ |
3 = 7. |
|||||
|
|
|
|
5 |
|
13 |
|
|
|
25 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Здесь |
θ =min |
(ω 5 |
=7, |
40-5-28)=7, |
|
|
|
20 |
|
20 |
|
13 |
7 |
40 |
|
B\A |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
строим цепочку [X42 |
X32 |
X35 ] и в ре- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
зультате аналогичной корректуры полу- |
|||||
|
20 |
|
|
|
|
|
5 |
|
25 |
|
|
|
|
|
3 |
||
X3 = |
|
|
|
|
|
0 |
7 |
28 |
|
35 |
|
чаем насыщающий поток X . |
|||||
|
|
|
|
|
|
Соответственно можем |
утверждать, |
||||||||||
|
8 |
|
|
|
7 |
|
15 |
|
|||||||||
|
|
|
|
|
|
|
|
|
что минимальное |
время транспорти- |
|||||||
|
|
|
|
12 |
|
13 |
|
|
|
25 |
|
ровки составляет 11 единиц. |
|||||
|
20 |
|
20 |
|
13 |
7 |
40 |
|
B\A |
|
Оба приведенных |
примера показы- |
|||||
вают, что решение транспортной задачи по критерию “минимума времени транспортировки” достаточно просто (на первых порах могут возникнуть заминки при построении цепочки).
8
3. Задачи
Найти решение транспортных задач по критерию времени при следующих данных :
1. |
B= |
15 |
15 |
20 |
10 |
A= |
2. |
B= |
7 |
7 |
7 |
7 |
7 |
A= |
|||||
|
|
|
3 |
7 |
9 |
4 |
11 |
|
|
|
|
8 |
3 |
2 |
6 |
5 |
15 |
||
|
T= |
1 |
5 |
10 |
5 |
29 |
|
|
T= |
4 |
3 |
5 |
8 |
2 |
5 |
||||
|
|
|
4 |
1 |
2 |
8 |
10 |
|
|
|
|
5 |
6 |
3 |
8 |
2 |
7 |
||
|
|
|
7 |
3 |
6 |
5 |
10 |
|
|
|
|
4 |
4 |
7 |
5 |
4 |
8 |
||
3. |
B= |
|
|
|
|
|
A= |
4. |
B= |
|
|
|
|
|
|
|
A= |
|
|
|
30 |
45 |
70 |
90 |
|
12 |
8 |
5 |
6 |
|
|
||||||||
|
|
|
1 |
2 |
3 |
7 |
60 |
|
|
|
|
5 |
8 |
3 |
4 |
|
|
11 |
|
|
T= |
9 1 |
4 |
1 |
80 |
|
|
T= |
6 |
2 |
1 |
8 |
|
|
7 |
|
|||
|
|
|
6 |
3 |
1 |
7 |
40 |
|
|
|
|
0 |
9 |
10 |
5 |
|
|
4 |
|
|
|
|
2 |
1 |
5 |
4 |
90 |
|
|
|
|
5 |
6 |
4 |
7 |
|
|
3 |
|
5. |
B= |
|
|
|
|
A= |
6. |
B= |
|
|
|
|
|
|
A= |
|
|||
12 |
18 |
14 |
20 |
20 |
20 |
15 |
15 |
|
|
|
|||||||||
|
|
|
5 |
7 |
6 |
4 |
10 |
|
|
|
|
1 |
3 |
6 |
4 |
|
|
15 |
|
|
T= |
2 |
1 |
3 |
8 |
14 |
|
|
T= |
3 |
4 |
4 |
3 |
|
|
20 |
|
||
|
|
|
6 |
8 |
6 |
4 |
16 |
|
|
|
|
6 |
5 |
2 |
2 |
|
|
15 |
|
|
|
|
11 |
6 |
7 |
8 |
18 |
|
|
|
|
9 |
8 |
6 |
7 |
|
|
20 |
|
7. |
B= |
|
|
|
|
|
A= |
8. |
B= |
11 |
12 |
3 |
8 |
|
|
15 |
A= |
||
|
|
|
|
|
|
|
|
|
|
||||||||||
9 |
10 |
7 |
13 |
8 |
18 |
17 |
16 |
15 |
10 |
||||||||||
|
|
|
5 |
6 |
4 |
3 |
2 |
17 |
|
|
|
5 |
8 |
4 |
3 |
2 |
15 |
||
|
T= |
1 |
8 |
3 |
5 |
6 |
8 |
|
T= |
1 |
3 |
7 |
8 |
2 |
10 |
||||
|
|
|
4 |
3 |
7 |
8 |
6 |
5 |
|
|
|
6 |
4 |
5 |
1 |
7 |
5 |
||
|
|
|
3 |
2 |
1 |
8 |
5 |
14 |
|
|
|
8 |
3 |
4 |
9 |
5 |
20 |
||
9. |
B= |
|
|
|
|
|
A= |
10. |
B= |
|
|
|
|
|
A= |
||||
5 |
7 |
8 |
9 |
4 |
9 |
10 |
11 |
12 |
7 |
||||||||||
|
|
|
3 |
4 |
5 |
6 |
7 |
15 |
|
|
|
8 |
1 |
9 |
3 |
6 |
5 |
||
|
T= |
8 |
9 |
10 |
1 |
2 |
6 |
|
T= |
4 |
5 |
1 |
7 |
7 |
6 |
||||
|
|
|
3 |
2 |
7 |
4 |
5 |
7 |
|
|
|
3 |
6 |
2 |
4 |
3 |
7 |
||
|
|
|
3 |
4 |
2 |
1 |
6 |
8 |
|
|
|
2 |
7 |
8 |
5 |
1 |
8 |
||
11. |
B= |
|
|
|
|
A= |
12. |
B= |
|
|
|
|
|
|
A= |
|
|||
15 |
28 |
35 |
10 |
7 |
14 |
12 |
10 |
|
|
|
|||||||||
|
|
|
9 |
3 |
10 |
12 |
21 |
|
|
|
|
1 |
4 |
5 |
8 |
|
|
8 |
|
|
T= |
1 |
7 |
13 |
15 |
28 |
|
|
T= |
7 |
8 |
3 |
5 |
|
|
16 |
|
||
|
|
|
7 |
5 |
3 |
4 |
35 |
|
|
|
|
3 |
0 |
4 |
6 |
|
|
14 |
|
|
|
|
8 |
2 |
9 |
1 |
10 |
|
|
|
|
2 |
4 |
9 |
1 |
|
|
12 |
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
13. |
B= |
|
|
|
|
A= |
14. |
B= |
|
|
|
|
|
|
A= |
10 |
30 |
50 |
10 |
10 |
10 |
15 |
5 |
10 |
10 |
||||||
|
|
5 |
4 |
9 |
11 |
11 |
|
|
5 |
8 |
6 |
3 |
4 |
1 |
12 |
|
T= |
7 |
1 |
8 |
3 |
40 |
|
T= |
8 7 |
6 |
3 |
4 |
2 |
18 |
|
|
|
2 |
10 |
3 |
4 |
20 |
|
|
1 |
8 |
3 |
7 |
2 |
9 |
10 |
|
|
5 |
6 |
5 |
7 |
9 |
|
|
2 |
7 |
4 |
6 |
3 |
8 |
10 |
15. |
B= |
|
|
|
|
|
A= |
16. |
B= |
|
|
|
|
|
A= |
5 |
8 |
11 |
12 |
18 |
14 |
16 |
20 |
30 |
20 |
||||||
|
|
8 |
9 |
0 |
7 |
1 |
3 |
|
|
3 |
4 |
5 |
6 |
7 |
13 |
|
T= |
5 |
4 |
3 |
1 |
5 |
4 |
|
T= |
2 |
8 |
9 |
6 |
11 |
23 |
|
|
6 |
7 |
10 |
2 |
8 |
17 |
|
|
3 |
4 |
4 |
5 |
1 |
33 |
|
|
3 |
6 |
6 |
8 |
4 |
20 |
|
|
1 |
2 |
3 |
4 |
7 |
43 |
17. |
B= |
|
|
|
|
|
A= |
18. |
B= |
|
|
|
|
A= |
|
7 |
3 |
8 |
9 |
10 |
16 |
26 |
30 |
10 |
|
||||||
|
|
1 |
0 |
7 |
4 |
5 |
11 |
|
|
8 |
5 |
6 |
7 |
17 |
|
|
T= |
8 |
9 |
3 |
1 |
2 |
10 |
|
T= |
3 |
4 |
2 |
1 |
27 |
|
|
|
5 |
6 |
3 |
7 |
9 |
20 |
|
|
9 |
10 |
11 |
2 |
37 |
|
|
|
|
|
|
|
|
|
|
|
5 |
6 |
3 |
4 |
7 |
|
|
|
|
|
|
|
|
|
|
|
1 |
8 |
3 |
4 |
10 |
|
19. |
B= |
|
|
|
|
A= |
|
20. |
B= |
|
|
|
|
A= |
|
5 |
15 |
10 |
20 |
|
27 |
31 |
45 |
19 |
|
||||||
|
|
3 |
4 |
1 |
2 |
10 |
|
|
|
5 |
7 |
6 |
8 |
45 |
|
|
T= |
2 |
1 |
7 |
5 |
10 |
|
|
T= |
3 |
4 |
5 |
7 |
17 |
|
|
|
6 |
2 |
4 |
1 |
15 |
|
|
|
2 |
1 |
9 |
11 |
13 |
|
|
|
5 |
6 |
3 |
4 |
15 |
|
|
|
15 |
13 |
3 |
1 |
28 |
|
21. |
B= |
|
|
|
|
A= |
|
22. |
B= |
|
|
|
|
A= |
|
20 |
20 |
30 |
60 |
|
13 |
15 |
17 |
19 |
|
||||||
|
|
8 |
3 |
5 |
1 |
18 |
|
|
|
2 |
7 |
4 |
8 |
14 |
|
|
T= |
3 |
4 |
8 |
5 |
28 |
|
|
T= |
5 |
8 |
3 |
1 |
16 |
|
|
|
4 |
1 |
6 |
10 |
36 |
|
|
|
7 |
12 |
4 |
9 |
18 |
|
|
|
12 |
7 |
9 |
2 |
48 |
|
|
|
4 |
5 |
10 |
7 |
20 |
|
23. |
B= |
|
|
|
|
A= |
|
24. |
B= |
|
|
|
|
|
A= |
10 |
11 |
12 |
18 |
|
8 |
10 |
12 |
12 |
5 |
||||||
|
|
3 |
4 |
5 |
6 |
11 |
|
|
|
5 |
4 |
3 |
2 |
1 |
11 |
|
T= |
7 |
8 |
9 |
9 |
12 |
|
|
T= |
1 |
2 |
3 |
4 |
5 |
18 |
|
|
1 |
2 |
3 |
4 |
13 |
|
|
|
7 |
8 |
3 |
4 |
5 |
13 |
|
|
5 |
6 |
7 |
8 |
14 |
|
|
|
8 |
9 |
6 |
11 |
3 |
14 |
25. |
B= |
|
|
|
|
A= |
|
26. |
B= |
|
|
|
|
A= |
|
3 |
7 |
9 |
2 |
|
15 |
15 |
20 |
40 |
|
||||||
|
|
2 |
5 |
2 |
2 |
4 |
|
|
|
5 |
8 |
3 |
4 |
20 |
|
|
T= |
4 3 |
7 |
5 |
5 |
|
|
T= |
1 |
2 |
5 |
6 |
10 |
|
|
|
|
6 |
2 |
1 |
8 |
6 |
|
|
|
3 |
4 |
7 |
8 |
30 |
|
|
|
3 |
7 |
3 |
9 |
8 |
|
|
|
8 |
9 |
5 |
3 |
10 |
|
