А.Г. Изместьев Уравнивание нивелирной сети коррелатным способом
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Государственное образовательное учреждение высшего профессионального образования
"КУЗБАССКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ"
Кафедра маркшейдерского дела и геодезии
УРАВНИВАНИЕ НИВЕЛИРНОЙ СЕТИ КОРРЕЛАТНЫМ СПОСОБОМ
Методические указания к лабораторной работе № 6 по курсу "Математическая обработка результатов геодезических измерений" для студентов специальности 311100 "Городской кадастр"
Составитель А.Г. Изместьев
Утверждены на заседании кафедры Протокол № 57 от 22.01.03 Рекомендованы к печати учебно-методической комиссией специальности 311100 Протокол № 25 от 18.02.03
Электронная копия находится в библиотеке главного корпуса ГУ КузГТУ
Кемерово 2003
1
Лабораторная работа № 6
УРАВНИВАНИЕ НИВЕЛИРНОЙ СЕТИ КОРРЕЛАТНЫМ СПОСОБОМ
Цель работы: освоить методику уравнивания нивелирной сети коррелатным способом.
1. Задание: выполнить уравнивание измеренных превышений и определить отметки точек 1, 2, 3 согласно заданному варианту (табл. 1) и схеме сети; определить средние квадратические погрешности уравненной отметки точки 1 и уравненного значения разности отметок Н2 – Н3.
Таблица 1
Исходные данные
№ |
Названия |
Превы- |
Длина |
Превы- |
Длина |
Превы- |
Длина |
хо- |
ходов |
шение |
L, км |
шение |
L, км |
шение |
L, км |
дов |
|
h, м |
|
h, м |
|
h, м |
|
1 |
2-3 |
Вариант |
1 |
Вариант |
2 |
Вариант |
3 |
−2,639 |
6,4 |
−2,758 |
4,2 |
−5,689 |
7,0 |
||
2 |
2-4 |
+5,321 |
7,2 |
+4,396 |
7,3 |
+2,547 |
9,1 |
3 |
3-4 |
+7,992 |
3,5 |
+7,196 |
5,6 |
+8,287 |
6,3 |
4 |
3-5 |
+4,562 |
7,5 |
+6,205 |
8,2 |
+4,625 |
9,6 |
5 |
4-5 |
−3,455 |
4,5 |
−1,022 |
4,8 |
−3,703 |
5,8 |
6 |
4-1 |
+0,181 |
5,2 |
+1,102 |
6,0 |
+2,959 |
6,5 |
7 |
5-1 |
+3,624 |
6,4 |
+2,103 |
7,5 |
+6,629 |
8,8 |
|
|
|
|
|
|
|
|
2
Продолжение табл. 1
№ |
Названия |
Превы- |
Длина |
Превы- |
Длина |
Превы- |
Длина |
хо- |
ходов |
шение |
L, км |
шение |
L, км |
шение |
L, км |
дов |
|
h, м |
|
h, м |
|
h, м |
|
1 |
2-3 |
Вариант |
4 |
Вариант |
5 |
Вариант |
6 |
−8,236 |
8,6 |
−6,283 |
5,6 |
−8,243 |
8,4 |
||
2 |
2-4 |
+4,088 |
12,3 |
+3,102 |
6,9 |
+1,967 |
7,2 |
3 |
3-4 |
+12,371 |
7,1 |
+9,352 |
4,3 |
+10,169 |
6,3 |
4 |
3-5 |
+6,954 |
10,6 |
+5,628 |
7,8 |
+2,741 |
9,4 |
5 |
4-5 |
−5,441 |
9,0 |
−3,681 |
5,6 |
−7,396 |
7,8 |
6 |
4-1 |
+1,406 |
11,0 |
+2,451 |
4,3 |
+3,571 |
9,6 |
7 |
5-1 |
+6,829 |
9,8 |
+6,157 |
6,7 |
+11,003 |
8,0 |
|
|
|
|
|
|
|
|
1 |
2-3 |
Вариант |
7 |
Вариант |
8 |
Вариант |
9 |
−6,183 |
3,8 |
−2,791 |
7,2 |
−4,538 |
8,1 |
||
2 |
2-4 |
+2,547 |
6,0 |
+5,153 |
8,5 |
+3,263 |
7,5 |
3 |
3-4 |
+8,703 |
5,2 |
+7,891 |
4,8 |
+7,770 |
5,2 |
4 |
3-5 |
+3,446 |
7,3 |
+6,136 |
8,3 |
+4,574 |
8,0 |
5 |
4-5 |
5,232 |
4,8 |
−1,718 |
6,1 |
−3,234 |
4,3 |
6 |
4-1 |
+2,996 |
6,1 |
+0,412 |
7,2 |
+2,279 |
8,7 |
7 |
5-1 |
+8,258 |
6,8 |
+2,166 |
9,1 |
+5,528 |
7,4 |
1 |
2-3 |
Вариант |
10 |
Вариант |
11 |
Вариант |
12 |
−3,657 |
10,5 |
−4,927 |
6,9 |
−5,329 |
15,3 |
||
2 |
2-4 |
+4,729 |
12,8 |
+5,012 |
5,4 |
+2,671 |
13,9 |
3 |
3-4 |
+8,428 |
8,0 |
+9,913 |
4,0 |
+8,017 |
9,8 |
4 |
3-5 |
+5,543 |
11,6 |
+6,895 |
8,4 |
+2,559 |
14,5 |
5 |
4-5 |
−2,842 |
6,9 |
−3,044 |
5,6 |
−5,417 |
8,6 |
6 |
4-1 |
+0,768 |
10,1 |
+0,548 |
9,1 |
+2,820 |
14,5 |
7 |
5-1 |
+3,593 |
9,7 |
+3,620 |
7,3 |
+8,217 |
12,7 |
3
Продолжение табл. 1
№ |
Названия |
Превы- |
Длина |
Превы- |
Длина |
Превы- |
Длина |
хо- |
ходов |
шение |
L, км |
шение |
L, км |
шение |
L, км |
дов |
|
h, м |
|
h, м |
|
h, м |
|
1 |
2-3 |
Вариант |
13 |
Вариант |
14 |
Вариант |
15 |
−8,693 |
7,5 |
−7,659 |
6,2 |
−6,072 |
7,8 |
||
2 |
2-4 |
+4,767 |
8,2 |
+0,986 |
5,3 |
+2,693 |
6,2 |
3 |
3-4 |
+13,434 |
5,1 |
+8,671 |
4,5 |
+8,798 |
5,0 |
4 |
3-5 |
+9,547 |
6,7 |
+4,516 |
7,8 |
+3,626 |
9,0 |
5 |
4-5 |
−3,855 |
3,8 |
−4,198 |
5,4 |
−5,191 |
4,6 |
6 |
4-1 |
+0,773 |
9,0 |
+4,501 |
8,7 |
+2,807 |
7,1 |
7 |
5-1 |
+4,641 |
6,9 |
+8,673 |
7,6 |
+7,987 |
6,8 |
|
|
|
|
|
|
|
|
1 |
2-3 |
Вариант |
16 |
Вариант |
17 |
Вариант |
18 |
|
|
|
|
|
|
||
−4,568 |
9,1 |
−3,762 |
6,9 |
−6,072 |
7,8 |
||
|
|
|
|
|
|
|
|
2 |
2-4 |
+5,219 |
8,5 |
+3,275 |
6,0 |
+2,693 |
6,2 |
3 |
3-4 |
+9,832 |
6,2 |
+6,986 |
4,3 |
+8,798 |
5,0 |
4 |
3-5 |
+7,673 |
7,4 |
+2,514 |
7,0 |
+3,626 |
9,0 |
5 |
4-5 |
−2,187 |
4,6 |
−4,442 |
3,4 |
−5,191 |
4,6 |
6 |
4-1 |
+0,285 |
8,3 |
+2,284 |
8,1 |
+2,807 |
7,1 |
|
|
|
|
|
|
|
|
7 |
5-1 |
+2,461 |
6,7 |
+6,749 |
7,6 |
+7,987 |
6,8 |
|
|
|
|
|
|
|
|
1 |
2-3 |
Вариант |
19 |
Вариант |
20 |
|
|
−8,901 |
12,1 |
−4,249 |
10,1 |
|
|
||
2 |
2-4 |
+1,798 |
10,9 |
+5,391 |
9,4 |
|
|
3 |
3-4 |
+10,663 |
7,2 |
+9,600 |
5,8 |
|
|
4 |
3-5 |
+4,139 |
8,0 |
+5,740 |
7,2 |
|
|
5 |
4-5 |
−6,500 |
6,3 |
−3,886 |
4,1 |
|
|
|
|
|
|
|
|
|
|
6 |
4-1 |
+3,767 |
9,3 |
+0,166 |
8,9 |
|
|
|
|
|
|
|
|
|
|
7 |
5-1 |
+10,294 |
8,1 |
+3,993 |
7,3 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
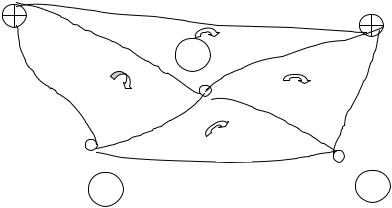
Схема нивелирной сети |
Ст.м. 1 (В) |
Гр.рп. 2(А) |
Н = 545,637 м |
Н = 540, 115 м |
6 |
1 |
IV |
2 |
|
|||
|
|
||
7 |
|
I |
1 |
III |
|
||
|
|
|
|
|
5 |
II 3 |
|
3 |
4 |
|
2 |
2.Содержание и последовательность выполнения работы
2.1.Вычертить схему нивелирной сети. Число полигонов (включая фиктивные) должно быть равно числу условных уравнений, т.е. r = n-k, где n – число ходов; k – число узловых (определяемых) точек. На схеме обозначить номера и направления ходов, направления подсчета невязок
вполигонах.
2.2.Составить систему условных уравнений вида
BV + W = 0, |
(2.1) |
где B – матрица коэффициентов; V – вектор поправок; W – вектор невязок.
2.3. Вычислить свободные члены по формуле
3
wi = ∑hi , (2.2)
i=1
где wj − невязка суммы превышений полигона; hi − превышение.
5
2.4. Составить оценочные функции. В оценку точности включить определение средних квадратических погрешностей уравненной отметки точки 1 и уравненного значения разности отметок точек 2 и 1.
F1 = HB - h6; F2 = H2 - H3 = - h4.
2.5. Вычислить веса превышений по формуле
Pi = 4Sкмi ,
где Si − длина хода.
2.6.Составить таблицы коэффициентов условных уравнений, оценочных функций и контрольных сумм. Знаки коэффициентов условных уравнений, равных ±1 и 0, определять по правилу: "+", если направление i-го хода совпадает с направлением подсчета невязок j-го полигона,
и"-", если наоборот.
2.7.Составить таблицу коэффициентов нормальных уравнений коррелат и коэффициентов, необходимых для вычисления обратных весов оценочных функций. Для этого можно использовать способ полигонов В.В. Попова, изложенный в лекции.
Контролем является выполнение равенств:
[taa] + [tab] + [tac] + [tad] = [tas]1 + F1 + F2 = [tas]2; |
(2.3) |
|
[tda] + [tdb] + [tdc] + |
[tdd] = [tds]1 + F1 + F2 = [tds]2, |
|
где ti – вес, равный 1/Рi; ai, bi, ci, di |
– коэффициенты условных уравне- |
|
ний. |
|
|
2.8. Решить нормальные уравнения по полной схеме Гаусса. Поря- |
||
док решения изложен в лекции. |
|
|
Осуществить контроль решения: |
|
|
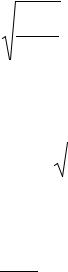
[tas]K1 + [tbs]K2 + [tcs]K3 + [tds]K4 + [w]=0; |
(2.4) |
|
[w54]= [tss54]= −[kw], |
|
|
6
где Ki – коррелата.
2.9. Вычислить поправки измеренных значений
vi = ti ai Ki + ti bi K2 + … + ti qi Kr. |
(2.5) |
|||
2.10. Вычислить уравненные значения превышений |
|
|||
h ур = hизм + v. |
|
|
(2.6) |
|
Подставить их в последнее условное уравнение для контроля. |
|
|||
2.11. Вычислить уравненные отметки точек |
|
|||
H j = Hисх ±hi . |
|
(2.7) |
||
2.12. Оценить точность по формулам |
|
|
|
|
µ = |
PV2 |
, |
(2.8) |
|
|
r |
|||
|
|
|
|
|
где µ − средняя квадратическая погрешность единицы веса;
m |
F |
= µ |
P−1 |
, |
(2.9) |
|
|
F |
|
|
|
|
1 |
|
|
|
|
где mF1 − средняя квадратическая погрешность функции F1;
mF2 = µ
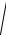PF−1 ,
где mF2 − средняя квадратическая погрешность функции F2.
7
3. Контрольный пример вычислений для варианта 5
Таблица 2
Исходные данные и результаты уравнивания
Номер хода |
Измеренное |
Длина хода, км |
Уравненное пре- |
|
превышение, м |
|
вышение, м |
1 |
−6,283 |
5,6 |
−6,2736 |
2 |
+3,102 |
6,9 |
+3,0751 |
3 |
+9,352 |
4,3 |
+9,3487 |
4 |
+5,628 |
7,8 |
+5,6470 |
5 |
−3,681 |
5,6 |
−3,7017 |
6 |
+2,451 |
4,3 |
+2,4469 |
7 |
+6,157 |
6,7 |
+6,1486 |
|
|
|
|
Составим условные уравнения. По замкнутым полигонам имеем:
h1 – h2 + h3 + w1 = 0;
−h3 + h4 – h5 + w2 = 0; h5 – h6 + h7 + w3 = 0.
По фиктивному полигону имеем
HA – HB + h2 + h6 + w4 = 0.
Вычислим свободные члены:
w1 = −6,283 – 3,102 + 9,352 = −33 мм; w2 = −9,352 + 5,628 + 3,681 = −43 мм; w3 = −3,681 – 2,451 + 6,157 = 25 мм;
w4 = 540,115 – 545, 637 + 3,102 + 2,451 = 31 мм.
Таким образом, условные уравнения имеют вид:
v1 – v2 + v3 – 33 = 0;
−v3 + v4 – v5 – 43 = 0; v5 + v7 – v6 + 25 = 0; v2 + v6 +31 = 0.
Составим оценочные функции
8
F1 = HB – h6; F2 = H2 – H3 = −h4.
Вычислим веса превышений.
|
|
|
|
|
|
|
|
|
Таблица 3 |
|
|
|
Коэффициенты условных уравнений |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
№ из- |
|
|
|
|
|
|
|
|
|
PV2 |
мере- |
P |
a |
b |
c |
d |
S1 |
F1 |
F2 |
S2 |
|
ния |
|
|
|
|
|
|
|
|
|
|
1 |
0,89 |
1 |
|
|
|
1 |
|
|
1 |
78,14 |
2 |
0,72 |
−1 |
|
|
1 |
0 |
|
|
0 |
521,77 |
3 |
1,16 |
1 |
−1 |
|
|
0 |
|
|
0 |
12,56 |
4 |
0,64 |
|
1 |
|
|
1 |
|
−1 |
0 |
231,53 |
5 |
0,89 |
|
−1 |
1 |
|
0 |
|
|
0 |
380,25 |
6 |
1,16 |
|
|
−1 |
1 |
0 |
−1 |
|
−1 |
19,28 |
7 |
0,75 |
|
|
1 |
|
1 |
|
|
1 |
52,92 |
W |
– |
−33 |
−43 |
25 |
31 |
– |
– |
– |
[PV2] |
=1296,45 |
Составим таблицы коэффициентов условных уравнений, оценочных функций контрольных сумм (табл. 3, 4).
Коэффициенты нормальных уравнений коррелат и коэффициенты для вычисления обратных весов оценочных функций приведены в табл. 5.
9
Таблица 4
Весовые коэффициенты
Номер |
t= |
1 |
|
ta |
tb |
tc |
td |
tS1 |
tF1 |
tF2 |
tS2 |
V, мм |
изме- |
|
|
||||||||||
|
P |
|
|
|
|
|
|
|
|
|
||
рения |
|
|
|
|
|
|
|
|
|
|
||
1 |
1,12 |
1,12 |
|
|
|
1,12 |
|
|
1,12 |
9,37 |
||
2 |
1,39 |
-1,39 |
|
|
1,39 |
0 |
|
|
0 |
-26,92 |
||
3 |
0,86 |
0,86 |
-0,86 |
|
|
0 |
|
|
0 |
- 3,29 |
||
4 |
1,56 |
|
1,56 |
|
|
1,56 |
|
-1,56 |
0 |
19,02 |
||
5 |
1,12 |
|
-1,12 |
1,12 |
|
0 |
|
|
0 |
-20,67 |
||
6 |
0,86 |
|
|
-0,86 |
0,86 |
0 |
0,86 |
|
-0,86 |
- 4,07 |
||
7 |
1,34 |
|
|
1,34 |
|
1,34 |
|
|
1,34 |
- 8,4 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
- |
|
|
8,37 |
12,19 |
-6,26 |
-11,0 |
- |
- |
- |
-[KW] |
=1298,24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 5
Коэффициенты нормальных уравнений
Коэффи- |
|
|
|
|
|
|
|
S2] |
циент |
a] |
b] |
c] |
d] |
S1] |
F1] |
F2] |
|
|
|
|
|
|
|
|
|
|
[ta |
3,37 |
−0,86 |
0 |
−1,39 |
1,12 |
0 |
0 |
1,12 |
|
|
|
|
|
|
|
|
|
[tb |
|
3,54 |
−1,12 |
0 |
1,56 |
0 |
−1,56 |
0 |
|
|
|
|
|
|
|
|
|
[tc |
|
|
−3,32 |
−0,86 |
1,34 |
0,86 |
0 |
2,2 |
|
|
|
|
|
|
|
|
|
[td |
|
|
|
2,26 |
0 |
−0,86 |
0 |
−0,86 |
|
|
|
|
|
|
|
|
|
[tF |
|
|
|
|
0 |
0,86 |
1,56 |
0 |
|
|
|
|
|
|
|
|
|
Нормальные уравнения решим по полной схеме Гаусса (табл. 6).