А.В. Бирюков Индуктивная статистика
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «КУЗБАССКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра высшей математики
ИНДУКТИВНАЯ СТАТИСТИКА
Методические указания к изучению соответствующего раздела программы курса математики для студентов
всех направлений
Составитель А. В. Бирюков
Утверждены на заседании кафедры Протокол № 1 от 25.08.02
Рекомендованы к печати учебнометодической комиссией специальности 290300 Протокол № 25 от 3.04.03
Электронная копия хранится в библиотеке главного корпуса ГУ КузГТУ
КЕМЕРОВО 2003
1
ВВЕДЕНИЕ
По определению А. Вальда статистика есть совокупность методов, которые дают возможность принимать оптимальные решения в условиях неопределенности. Если дискриптивная статистика ограничивается описанием полных совокупностей, то современная индуктивная или аналитическая статистика исследует только репрезентативную часть совокупности, называемую выборкой. Результат исследования выборки по индукции распространяется на всю генеральную совокупность.
Основными числовыми характеристиками выборки, содержащей N элементов
X1 , X 2 ,..., X N ,
являются выборочное среднее
X = ( X1 +... + X N ) / N
и выборочная дисперсия |
|
|
|
|
||
S 2 = (X1 − |
|
)2 |
+... + (X N − |
|
)2 |
(N −1). |
X |
X |
|||||
|
|
|
|
|
||
|
|
|
|
|
||
Число N называется объемом выборки, а число (N −1) – числом степеней свободы выборочной дисперсии. Все выборочные характеристики называют статистиками.
Если неизвестный генеральный параметр оценивается соответствующей статистикой с указанием интервала, которому он принадлежит с заданной вероятностью, то этот интервал называется доверительным интервалом, а заданная вероятность – доверительной вероятностью или надежностью утверждения. Разность между единицей и доверительной вероятностью называется уровнем значимости.
При проверке статистических гипотез возможны два ошибочных решения – отклонить верную гипотезу и принять неверную гипотезу. Вероятность первой ошибки равна уровню значимости.
Критерии, которые служат для проверки гипотез и не предполагают известным закон распределения случайной величины, называются непараметрическими. Непараметрическая статистика обладает тем преимуществом, что требует сравнительно простых вычислений. Поэтому ее методы называют «быстрыми».
2
1. ПРОВЕРКА ГИПОТЕЗ
При проверке гипотез будем предполагать уровень значимости равным 0,05. В этом случае надежность выводов составляет 95%.
2.1. Однородность выборки
Выборка называется однородной, если она не содержит ошибочных элементов. Ошибочный элемент может быть либо самый большой,
либо самый малый. Обозначим сомнительный элемент через X 0 . Тогда вопрос об его ошибочности решает статистика
C = X 0 − X S ,
где X – выборочное среднее, S – стандарт (корень квадратный из выборочной дисперсии).
Сомнительный элемент отбрасывается как ошибочный, если вычисленное значение статистики превосходит критическое. В табл.1 приведены критические значения статистики в зависимости от объема выборки N .
N |
|
|
|
|
|
Таблица 1 |
4 |
6 |
8 |
10 |
12 |
14 |
|
C |
1,7 |
2,0 |
2,2 |
2,3 |
2,4 |
2,5 |
N |
16 |
18 |
20 |
22 |
24 |
26 |
C |
2,5 |
2,6 |
2,6 |
2,7 |
2,7 |
2,7 |
2.2. Нормальность выборки
Выборка называется нормальной, если она извлечена из нормально распределенной генеральной совокупности. Проверка выборки на нормальность состоит в вычислении статистики
C = R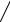 
S ,
где R – размах выборки, равный разности между наибольшим и наименьшим элементами.
Если вычисленное значение статистики принадлежит критическому интервалу
A < C < B ,
3
то выборку можно считать нормальной.
В табл. 2 приведены границы критического интервала в зависимости от объема выборки N .
N |
A |
|
N |
A |
Таблица 2 |
B |
B |
||||
7 |
2,4 |
3,2 |
40 |
3,7 |
5,2 |
8 |
2,5 |
3,4 |
50 |
3,8 |
5,4 |
9 |
2,6 |
3,6 |
60 |
4,0 |
5,5 |
10 |
2,7 |
3,7 |
80 |
4,2 |
5,7 |
16 |
3,0 |
4,2 |
100 |
4,3 |
5,9 |
20 |
3,2 |
4,5 |
200 |
4,8 |
6,4 |
30 |
3,5 |
4,9 |
500 |
5,4 |
6,9 |
2.3. Сравнение дисперсий
Для двух произвольных выборок с одинаковыми объемами N и
размахами R1 , R2 ( R1 > R2 ) статистика, принадлежащая Пиллаи, имеет вид
C = R1 
R 2 .
Если значение статистики не превосходит критическое (табл. 3), то дисперсии выборок отличаются друг от друга незначимо (т.е. случайно).
N |
|
|
|
|
Таблица 3 |
6 |
7 |
8 |
9 |
10 |
|
C |
2,3 |
2,1 |
2,0 |
1,9 |
1,8 |
Для двух нормальных выборок с дисперсиями S12 , S22 (S12 > S22 ) можно применить более мощный критерий Фишера со статистикой
C = S 12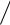 
S 22 .
Если это отношение дисперсий больше критического, то различие между дисперсиями значимо (неслучайно). В табл. 4 приведены критические значения для случая, когда выборки имеют одинаковый объем
N .
Таблица 4
N −1 |
10 |
15 |
20 |
30 |
40 |
C |
3,0 |
2,4 |
2,1 |
1,8 |
1,7 |
4
Если имеется M нормальных выборок одинакового объема N , то сравнение их дисперсий можно провести по критерию Хартли со статистикой
C = max S 2 min S 2 , |
равной отношению наибольшей дисперсии к наименьшей. Если это отношение превосходит критическое значение (табл. 5), то дисперсии от-
личаются значимо. |
|
|
|
|
Таблица 5 |
M , N |
|
|
|
|
|
10 |
15 |
20 |
30 |
60 |
|
3 |
4,8 |
3,5 |
3,0 |
2,4 |
1,8 |
4 |
5,7 |
4,0 |
3,3 |
2,6 |
2,0 |
5 |
6,3 |
4,4 |
3,5 |
2,8 |
2,0 |
6 |
6,9 |
4,7 |
3,8 |
2,9 |
2,1 |
7 |
7,4 |
5,0 |
3,9 |
3,0 |
2,2 |
8 |
7,9 |
5,2 |
4,1 |
3,1 |
2,2 |
9 |
8,3 |
5,4 |
4,2 |
3,2 |
2,3 |
10 |
8,7 |
5,6 |
4,4 |
3,3 |
2,3 |
2.4. Сравнение средних
Для двух произвольных выборок с одинаковыми объемами N ,
выборочными средними X1 , X 2 и размахами R1 , R2 вопрос о сравнении средних решает статистика Лорда
C = 2 X1 − X 2 
(R1 + R2 ).
Если найденное значение статистики превосходит критическое (табл. 6), то различие между средним значимо.
N |
|
|
|
|
|
Таблица 6 |
3 |
4 |
5 |
6 |
7 |
8 |
|
C |
1,27 |
0,83 |
0,61 |
0,50 |
0,43 |
0,37 |
N |
9 |
10 |
11 |
12 |
13 |
14 |
C |
0,33 |
0,30 |
0,28 |
0,26 |
0,24 |
0,23 |
N |
15 |
16 |
17 |
18 |
19 |
20 |
C |
0,22 |
0,21 |
0,20 |
0,19 |
0,18 |
0,17 |
Для M выборок одинакового объема со средними
X1 > X 2 > ... > X M
5
имеет статистику Диксона
C = X1 − X 2 
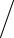
X1 − X M .
Если значение статистики превосходит критическое (табл. 7), то наибольшее среднее значимо отличается от остальных. Аналогичным образом решается вопрос относительно наименьшего среднего, когда
X1 < X 2 <... < X M
|
|
|
|
|
Таблица 7 |
M |
3 |
4 |
5 |
6 |
7 |
C |
0,94 |
0,76 |
0,64 |
0,56 |
0,51 |
2.5. Сравнение выборок
Для двух выборок одинакового объема N проверяется гипотеза: обе выборки извлечены из одной и той же генеральной совокупности. Вопрос решает критерий Вилкоксона.
Обе выборки объединяем в одну совокупность и располагаем элементы по возрастанию, помечая (например, штрихом) элементы одной из выборок. В объединенной совокупности элементы нумеруем в порядке возрастания. Номер элемента называется его рангом. Одинаковым по величине элементам присваиваем средний в их группе ранг.
Далее подсчитываем суммы рангов элементов каждой выборки и находим величины
|
|
C |
1 |
= N 2 |
+ 0,5N(N +1)− D |
, |
|
||
|
|
|
|
|
|
1 |
|
||
|
|
C2 |
= N 2 +0,5N(N +1)− D2 . |
|
|||||
Искомая статистика равна наименьшему из чисел C1 ,C2 |
т.е. |
||||||||
|
|
|
|
C = min |
(C 1 , C 2 |
). |
|
|
|
Если найденное значение статистики больше критического (табл. |
|||||||||
8), то сформулированная гипотеза верна. |
|
|
Таблица 8 |
||||||
N |
|
|
|
|
|
|
|
|
|
5 |
6 |
|
7 |
8 |
9 |
10 |
11 |
12 |
|
C |
4 |
7 |
|
11 |
15 |
21 |
27 |
34 |
42 |
N |
13 |
14 |
|
15 |
16 |
17 |
18 |
19 |
20 |
C |
51 |
61 |
|
72 |
83 |
96 |
109 |
123 |
138 |
6
Аналогичным образом решается задача для M выборок с объемами N . В этом случае решение дает статистика
C = |
12 (D12 + ... DM2 ) |
− 3(MN +1). |
MN 2 (MN +1) |
Если найденное значение статистики меньше критического (табл. 9), то все выборки принадлежат одной и той же генеральной совокупности.
|
|
|
|
|
|
Таблица 9 |
M −1 |
2 |
3 |
4 |
5 |
6 |
7 |
C |
6,0 |
7,8 |
9,5 |
11 |
13 |
14 |
M −1 |
8 |
9 |
10 |
11 |
12 |
13 |
C |
16 |
17 |
18 |
20 |
21 |
22 |
M −1 |
14 |
15 |
16 |
17 |
18 |
19 |
C |
24 |
25 |
26 |
28 |
29 |
30 |
M −1 |
20 |
21 |
22 |
23 |
24 |
25 |
C |
31 |
33 |
34 |
35 |
36 |
37 |
Приведем пример сравнения двух выборок по критерию Вилкоксона. Имеются выборки: 1) 1, 1, 3, 4, 5; 2) 1, 2, 6, 7, 8. Элементы объединенной совокупности
1, 1, 1`, 2`, 3, 4, 5, 6`, 7`, 8` |
|
имеют ранги 2, 2, 2, 4, 5, 6, 7, 8, 9, 10. При этом C1 =18 , |
C2 = 7 . Иско- |
мая статистика C = 7 больше критического значения, |
которое при |
N = 5 равно 4. Следовательно, обе данные выборки принадлежат одной генеральной совокупности.
3. КОРРЕЛЯЦИЯ
Рассмотрим две случайные величины X и Z , которые из некоторых априорных соображений будем считать связанными друг с другом. Отвлекаясь от истинного характера этой взаимосвязи, остановимся лишь на близости этой зависимости к линейной, называемой корреляцией.
3.1. Коэффициент корреляции
Пусть имеются результаты одновременного наблюдения за двумя случайными величинами
7
(X k , Z k ), k =1,2,...N .
Вычислим статистику
C = (XZ − X Z )
S 1 S 2 ,
называемую выборочным коэффициентом корреляции. Здесь XZ - среднее произведение, а S1 и S2 – выборочные стандарты.
Эта статистика может принимать значения в интервале от -1 до +1. Если найденное значение превосходит критическое (табл. 10), то корреляция между случайными величинами значима.
N |
|
|
|
|
Таблица 10 |
6 |
8 |
10 |
15 |
20 |
|
C |
0,71 |
0,63 |
0,58 |
0,48 |
0,42 |
N |
30 |
40 |
50 |
70 |
90 |
C |
0,35 |
0,30 |
0,27 |
0,23 |
0,20 |
3.2. Ранговая корреляция
Пусть, как и прежде, имеются пары наблюдений
(X k , Zk ), k =1,2,...N .
Значения Xk и Zk независимо друг от друга расположим по воз-
растанию и ранжируем, приписывая ранги 1, 2, 3 и т.д. в порядке возрастания элементов выборок. Разность рангов у соответствующих друг
другу элементов Xk и Zk обозначим через Ek . Далее вычислим статистику Спирмена
C = 1 − 6(E12 + ... + EN2 )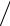
N (N 2 −1).
Корреляция признается значимой, если найденное значение статистики превосходит критическое (табл. 11).
N |
|
|
|
|
|
Таблица 11 |
6 |
8 |
10 |
12 |
14 |
16 |
|
C |
0,77 |
0,60 |
0,55 |
0,50 |
0,46 |
0,42 |
N |
18 |
20 |
22 |
24 |
26 |
28 |
C |
0,40 |
0,38 |
0,36 |
0,34 |
0,33 |
0,32 |
8
3.3. Адекватность регрессии
Если при проверке гипотезы о корреляции оказалось, что корреляция значима, то правомерно искать линейную зависимость между X и Z , называемую регрессией или регрессионной моделью. Используя метод наименьших квадратов, найдем эту модель в виде
Z = Z +W (X − X ),
где угловой коэффициент регрессии равен
W = (XZ − X Z )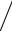
(X 2 − X 2 ).
Здесь X , Z – выборочные средние; XZ - среднее произведение;
X 2 – средний квадрат; X 2 – квадрат среднего.
Для проверке адекватности найденной модели необходимо найти две дисперсии – остаточную дисперсию S 2 , характеризующую точ-
ность модели, и дисперсию воспроизводимости S02 , характеризующую
уровень шума, т.е. совокупное влияние случайных факторов. Для вычисления последней необходимо иметь дублирующие (параллельные) наблюдения, т.е. значения Z при фиксированном значении X . Диспер-
сия параллельных наблюдений равна S02 .
Для вычисления остаточной дисперсии найдем сумму квадратов разностей между экспериментальными и вычисленными по модели
значениями Z . Разделив эту сумму на N −2 , где N – число пар на-
блюдений (объем выработки), получим остаточную дисперсию S 2 . Если при сравнении по какому-либо критерию (Пиллаи или Фи-
шера) окажется, что различие между дисперсиями S 2 и S02 незначимо, то найденная регрессионная модель адекватна.
4. ФАКТОРНЫЙ АНАЛИЗ
Рассмотрим некоторый сложный процесс с выходным параметром X . Таким процессом является, например, работа какого-либо предприятия, эффективность которой характеризуется выходным параметром – себестоимостью выпускаемой продукции.
На вариацию значений выходного параметра влияет множество различных факторов. Из некоторых априорных соображений (напри-
9
мер, из предыдущего опыта) выделим из множества факторов основную группу, подлежащую изучению. Ограничимся случаем, когда основная группа состоит из двух факторов F , G . Кроме них на выходной параметр оказывает влияние множество случайных факторов. Поэтому общая дисперсия значений выходного параметра является суммой факторных дисперсий и дисперсии случайности, т.е.
S 2 = S12 + S 22 + S 02 .
Задача факторного анализа состоит в представлении общей дисперсии в виде такой суммы, а также в оценке силы влияния каждого фактора. Рассмотрим последовательно факторный анализ с одним и двумя основными факторами.
4.1. Однофакторный анализ
Для конкретности допустим, что фактор F варьируется на трех уровнях и на каждом уровне имеется по три параллельных на-
блюдения. Тогда соответствующая матрица значений выходного параметра имеет вид
X11 |
X 21 |
X 31 |
X12 |
X 22 |
X 32 |
X13 |
X 23 |
X 33 |
Здесь первый индекс у элемента матрицы соответствует уровню фактора. Введем следующие обозначения:
U1 ,U2 ,U3 – сумма элементов в столбцах матрицы;
Q – сумма квадратов всех элементов матрицы;
Q1 = (U12 +U 22 +U 32 )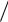
3 ;
P – квадрат суммы всех элементов матрицы, деленный на 9; SF2 – вспомогательная дисперсия.
Тогда имеют место следующие формулы:
S02 =(Q −Q1 ) 6 ; |
SF2 =(Q1 −P) 2. |
Если различие между дисперсиями SF2 и S02 , проверяемое по како- му-либо критерию, оказывается значимым, то исследуемый фактор