
В.М. Волков Математика и математика в экономике. Контрольные задания №3, 4 и методические указания для студентов заочной формы обучения экономических специальностей 1 курса (2 семестр)
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ГОСУДАРСТВЕННОЕ УЧРЕЖДЕНИЕ КУЗБАССКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИ-
ВЕРСИТЕТ
Кафедра прикладной математики
МАТЕМАТИКА И МАТЕМАТИКА В ЭКОНОМИКЕ
Контрольные задания № 3, 4 и методические указания для студентов заочной формы обучения экономических специальностей 1 курса ( 2 семестр )
(в том числе сокращённые сроки обучения)
Составитель В.М. Волков
Утверждены на заседании кафедры Протокол № 5 от 4.03.01 Рекомендованы к печати учебнометодической комиссией ИЭФ Протокол № 3 от 6.03.01
Электронная копия находится в библиотеке главного корпуса ГУ КузГТУ
Кемерово 2001
1
Контрольные работы № 3,4 составлены в соответствии с программой курса высшей математики для студентов-заочников. В составлении работ и методических указаний к ним принимали участие преподаватели: В.М.Волков, Е.А.Волкова, В.А.Гоголин, О.А.Зубанова, И.А.Ерма-кова, В.И.Немов, В.А.Похилько, Е.В.Прейс, С.М.Швыдко.
Номера задач контрольных работ студент должен выбрать по таблице «Выбор номеров контрольных задач» следующим образом:
найти строку, соответствующую первой букве фамилии; найти столбец, соответствующий последней цифре шифра;
на пересечении найденных строки и столбца взять номера задач контрольных работ № 3,4.
Контрольные работы, выполненные не по своему варианту, возвращаются непроверенными.
ПРОГРАММА 1 КУРСА (2 СЕМЕСТР )
1.Дифференциальное исчисление функции одной переменной
1.1.Производная функции, её геометрический и физический смысл. Правила дифференцирования. Логарифмическое дифференцирование. Производные функций, заданных неявно и параметрически.
Правило Лопиталя.
1.2.Дифференциал функции. Применение дифференциала к приближённым вычислениям.
1.3.Производные и дифференциалы высших порядков.
1.4.Условия возрастания и убывания функции. Точки экстремума. Необходимый и достаточный признаки существования экстремума.
1.5.Теорема о функции, непрерывной на замкнутом интервале. Отыскание наибольшего и наименьшего значений функции, непрерывной на замкнутом интервале. Применение теории экстремума к решению задач.
1.6.Выпуклость, вогнутость графика функции. Точки перегиба. Необходимый и достаточный признаки существования точек перегиба.
1.7.Асимптоты графика функции и способы их отыскания. Общая схема исследования функции и построения её графика.

|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
Выбор номеров задач контрольных работ |
|
|
|
||||
|
|
|
|
|
|
|
6 |
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
7 |
8 |
9 |
|
|
|
|
|
|
|
|
7 37 74 |
|
|
|
А,В, |
1 31 80 |
2 32 79 |
3 33 78 |
4 34 77 |
5 35 76 |
6 36 75 |
8 38 73 |
9 39 72 |
10 40 71 |
|
Д |
110 130 |
100 150 |
101 131 |
120 130 |
91 141 |
110 140 |
111 121 |
100 150 |
101 131 |
120 130 |
|
|
|
|
|
|
|
17 47 64 |
|
|
|
Б,Ё,З |
11 41 70 |
12 42 69 |
13 43 68 |
14 44 67 |
15 45 66 |
16 46 66 |
18 48 63 |
19 49 62 |
20 50 61 |
|
|
109 129 |
99 149 |
102 132 |
119 129 |
92 142 |
109 139 |
112 122 |
99 149 |
102 132 |
119 129 |
|
|
|
|
|
|
|
27 57 74 |
|
|
|
Г,Ж, |
21 51 80 |
22 52 79 |
23 53 78 |
24 54 77 |
25 55 76 |
26 56 75 |
28 58 79 |
29 59 72 |
30 60 71 |
|
И,Л |
108 128 |
98 148 |
103 133 |
118 128 |
93 143 |
108 138 |
113 123 |
98 148 |
103 133 |
118 128 |
|
|
|
|
|
|
|
7 54 84 |
|
|
|
К |
1 60 90 |
2 59 89 |
3 58 88 |
4 57 87 |
5 56 86 |
6 55 85 |
8 53 83 |
9 52 82 |
10 51 81 |
|
|
107 127 |
97 147 |
104 134 |
117 127 |
94 144 |
107 137 |
114 124 |
97 147 |
104 144 |
117 127 |
|
|
|
|
|
|
|
17 43 66 |
|
|
|
М,Н, |
11 49 70 |
12 48 61 |
13 47 62 |
14 46 63 |
15 45 64 |
16 44 65 |
18 50 67 |
19 42 68 |
20 41 69 |
|
О |
106 126 |
96 146 |
105 135 |
116 126 |
95 145 |
106 136 |
115 125 |
96 146 |
105 135 |
116 126 |
|
|
|
|
|
|
|
27 37 76 |
|
|
|
П,Ы |
21 31 80 |
22 32 71 |
23 33 72 |
24 34 73 |
25 35 74 |
26 36 75 |
28 38 77 |
29 39 76 |
30 40 79 |
|
|
105 125 |
95 145 |
106 136 |
115 125 |
96 146 |
105 135 |
116 126 |
95 145 |
106 136 |
115 125 |
|
|
|
|
|
|
|
7 54 86 |
|
|
|
С,У, |
1 60 90 |
2 59 81 |
3 58 82 |
4 57 83 |
5 56 84 |
6 55 85 |
8 53 87 |
9 52 88 |
10 51 89 |
|
Е |
104 124 |
94 144 |
107 137 |
114 124 |
97 147 |
104 134 |
117 127 |
94 144 |
107 137 |
114 124 |
|
|
|
|
|
|
|
17 44 66 |
|
|
|
Р,Т, |
11 50 70 |
12 49 61 |
13 48 62 |
14 47 63 |
15 46 64 |
16 45 65 |
18 43 67 |
19 42 68 |
20 41 69 |
|
Ф |
103 123 |
93 143 |
108 138 |
113 123 |
98 148 |
103 133 |
118 128 |
93 143 |
108 138 |
113 123 |
|
|
|
|
|
|
|
27 34 76 |
|
|
|
Х,Ц, |
21 40 80 |
22 39 71 |
23 38 72 |
24 37 73 |
25 36 74 |
26 36 75 |
28 33 77 |
29 32 78 |
30 31 79 |
|
Ш |
102 122 |
92 142 |
109 139 |
112 122 |
99 149 |
102 132 |
119 129 |
92 142 |
108 139 |
112 122 |
|
|
|
|
|
|
|
7 57 86 |
|
|
|
Ч,Щ, |
1 51 90 |
2 52 81 |
3 53 82 |
4 54 83 |
5 55 84 |
6 56 85 |
8 58 87 |
9 59 88 |
10 60 89 |
|
Э,Ю, |
101 121 |
91 141 |
110 140 |
111 121 |
100 150 |
101 131 |
120 130 |
91 141 |
110 140 |
111 121 |
Я |
|
|
|
|
|
|
|
|
|
|

2. Функции нескольких переменных 2.1.Понятие функции нескольких переменных. Область определения.
Непрерывность.
2.2. Частные производные первого порядка. Полный дифференциал функции, его применение к приближённым вычислениям.
2.3.Касательная плоскость к поверхности. Частные производные высших порядков.
2.4.Экстремум функции двух переменных. Наибольшее и наименьшее значения функции двух переменных.
2.5.Градиент. Производная функции двух переменных по направле-
нию.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К КОНТРОЛЬНЫМ РАБОТАМ
Контрольная работа № 3
В данную контрольную работу включены задачи дифференциального исчисления функции одной переменной [1, гл.6].
Для решения задач № 1-30 необходимо изучить литературу [1, гл.6, п.п.1-3]. Особое внимание следует обратить на правило дифференцирования сложной функции. Например, y = tg3 2x сложная функция, так как она может быть представлена в виде композиции элементарных функций. Задана степенная функция y = u3 , её аргумент u = tgv явля-
ется тригонометрической функцией, аргумент v которой в свою очередь является функцией от x: v = 2x . По правилу дифференцирования
сложной функции имеем
y′x = y′u u′v v′x = 3u2 cos12 v 2.
Подставляя вместо u, v их выражения через x, получим
y′ = 3 tg2 |
2x |
1 |
2 |
= |
6tg2 2x |
. |
|
|
|||||
x |
|
cos2 2x |
|
|
cos2 2x |
|
|
|
|
|
|
Пример. Найти дифференциал функции y =  e2x − 4 − ln2 3x . Решение. Дифференциал функции равен dy = y′ dx . Найдём произ-
e2x − 4 − ln2 3x . Решение. Дифференциал функции равен dy = y′ dx . Найдём произ-
водную, применяя правила дифференцирования разности функций и сложной функции, получим

4
|
|
|
|
1 |
|
′ |
|
′ |
|
|
|
|
− |
1 |
|
|
|
|
|
(e2x |
|
|
− ((ln 3x)2 ) |
1 (e2x |
− 4) |
2 e2x |
2 − 2ln 3x |
3 |
|||||||||
dy = |
− 4)2 |
dx = |
|
dx = |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
2x |
− 2ln 3x |
|
|
|
|
|
|
|
|
|
|
|
|
|||
= |
|
dx. |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
e2x − 4 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример. Найти дифференциал функции y = |
x5−x 2 |
. |
|
|
||||||||||||||
cos2 x |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение. Так как функция представляет собой частное двух функ- |
||||||||||||||||||
ций, то при нахождении производной применяем правило дифференцирования частного двух функций и при нахождении производной функции в числителе используем правило дифференцирования произ- ведения функций. Получаем
|
|
|
|
|
5−x |
2 |
+ x |
5−x |
2 |
) |
′ |
2 x − (cos2 x) |
′ |
x5 |
|
2 |
|
|
|
|
|
(x)′ |
|
|
cos |
|
−x |
|
|
|
|||||||
dy = |
|
|
|
|
( |
|
|
|
|
|
|
|
|
dx = |
||||
|
|
|
|
|
|
|
cos4 x |
|
|
|
|
|
||||||
|
[5−x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
+ x5−x 2 |
ln 5(− 2x)]cos2 x − 2cosx(− sin x)x5−x 2 |
||||||||||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx = |
|
|
|
|
|
|
|
|
|
|
cos4 x |
|
|
|
|
|
|||
= |
5−x 2 (cosx − 2x2 ln 5 cosx + 2x sin x) |
dx. |
|
||
|
cos3 x |
|
При решении задач № 1-30 (п. г)) следует использовать метод логарифмического дифференцирования.
Пример. Найти дифференциал функции y = (x2 + 7)arcsin x .
Решение. Так как основание и показатель являются функциями, то предварительно прологарифмируем данную функцию
ln y = arcsin x ln(x2 + 7).
Дифференцируем полученное равенство по переменной x
(ln y)′ = (arcsin x ln(x2 + 7))′.
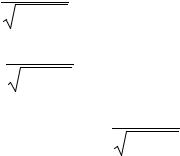
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
1 |
y′ = |
1 |
ln(x2 |
+ 7)+ arcsin x |
|
|
1 |
|
2x. |
|
|
|
|
|||
y |
1 − x2 |
x2 + 7 |
|
|
|
|
|
|||||||||
|
|
1 |
ln(x2 |
+ 7)+ arcsin x |
|
1 |
|
|
|
|
|
|
|
|
||
y′ = y |
|
|
|
|
2x . |
|
|
|
|
|||||||
1 − x2 |
x |
2 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
+ 7 |
|
|
|
|
|
|||||
dy = (x2 + 7)arcsin x |
1 |
ln(x2 + 7)+ arcsin x |
|
2x |
|
dx. |
||||||||||
1 − x2 |
x |
2 |
7 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|||
Для решения задач № 31-60 следует использовать литературу [1,
гл.6, п.2; 2, гл.6, п.2].
Пример. Для функции y = ln(sin 3x) найти значения производных
dy |
|
и |
|
d2y |
при x = |
π |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
dx |
|
|
dx2 |
6 |
1 |
|
|
|
|
|
|
|
|
cos 3x 3 |
|
|
|
|||||||||||||||
|
|
|
|
|
dy |
|
|
|
|
|
(sin 3x)′ |
|
|
|
|
|||||||||||||||||
|
|
Решение. |
= y′ |
= |
|
|
= |
= 3ctg3x . |
||||||||||||||||||||||||
|
|
dx |
sin 3x |
sin 3x |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−1 |
|
|
|
|
|
||
y |
|
|
|
d |
dy |
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
) |
|
|
9 |
|
|
||||||
d |
= |
|
= y′′ |
= (3ctg3x) |
= |
3 |
|
3 |
= − |
|
. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
dx2 |
|
dx |
|
sin2 |
3x |
sin2 |
3x |
|||||||||||||||||||||||||
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
dy |
|
|
|
|
|
= |
|
|
|
3 |
|
π |
|
= |
3ctg |
π |
= 0 . |
|
|
|
|
|
|
|
|
|
||||||
dx |
|
|
π |
|
3ctg |
6 |
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
x= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d2y |
|
|
|
π = − |
|
|
|
9 |
|
|
|
= −9 . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
dx2 |
x= |
|
|
2 |
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
6 |
|
|
sin |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для решения задач №61-90 необходимо знать, что наибольшее и наименьшее значения функции на замкнутом интервале могут достигаться в критических точках, принадлежащих интервалу, или на границах интервала.
Пример. Найти наибольшее и наименьшее значения функции f (x)= 13 x3 − 52 x2 − 6x + 9 на отрезке [0,8].
Решение. Найдём критические точки, для этого производную функции приравняем к нулю f ′(x)= x2 − 5x − 6 = 0. Корни этого уравнения
x1 = −1; x2 = 6 . Отрезку [0,8] принадлежит только точка x2 = 6 . Най-

6
дём значения функции в данной критической точке и на концах интер-
вала f (6)= −45; f (0)= 9; f (8)= −28 |
1 . |
|
3 |
Итак, наибольшее значение функции равно 9 и достигается в точке x = 0. Наименьшее значение функции равно -45 и достигается в точке x = 6.
При решении задач № 91-120 труднее всего записать выражение оптимизируемой функции по указанным свойствам.
Пример. Закрытый бак имеет форму цилиндра. При данном объёме V каковы должны быть радиус основания и высота бака, чтобы расход материала на его изготовление был наименьшим.
Решение. Оптимизируемая функция - полная поверхность цилиндра
S = Sбок + 2Sосн = 2πrh + 2πr2 .
Это функция двух переменных r и h. Выразим одну переменную через другую, используя условие, что объём цилиндра должен остаться по-
стоянным, равным V . V = πr2h , отсюда h = πVr2 . Подставим это вы-
ражение в оптимизируемую функцию S , получим S = 2πr πVr2 + 2πr2 ,
S = 2rV + 2πr2 . Теперь функция S записана как функция одной пере-
менной r . Задача сводится к исследованию функции S(r) на экстремум
(минимум) [1, гл.6, п.7; 2, гл.7, п.2].
Так как функция определена на открытом промежутке (0, ∞), то она
может достигать наименьшего значения только в критических точках |
||
этого промежутка. Найдём производную и приравняем её к нулю |
||
S′(r)= − 2V + 4πr = |
2(2πr3 − V) |
. |
|
||
r2 |
r2 |
|
S′(r)= 0 2πr3 − V = 0 r = 3 2Vπ .
Покажем, что в этой критической точке функция S(r) достигает минимума. Найдём S′′(r):
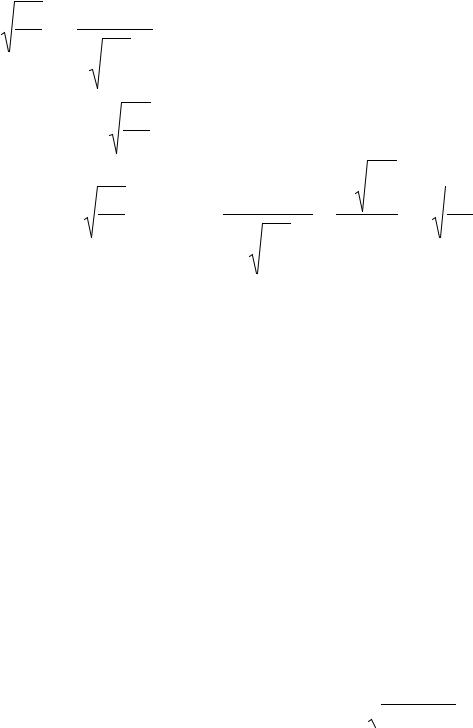
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
S′′(r)= |
( |
S′(r) |
) |
′ |
= |
|
− |
2V |
′ |
= |
4V |
+ 4π, |
|
|
|
||||||||
|
|
r2 |
+ 4πr |
|
r3 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
V |
|
|
= |
|
4V |
|
+ 4π = 12π f 0 , |
|
|
|
|
|
|
|
||||||||
S′′ 3 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
2π |
|
|
|
|
V |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то есть при r = |
3 |
V |
функция S(r) |
|
имеет минимум. Определим высоту |
||||||||||||||||||
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
V |
|
|
|
|||
|
|
|
|
|
|
|
V |
|
|
|
|
V |
|
|
|
V3 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 23 V . |
||||||
бака при r = 3 |
|
|
h = |
|
|
|
|
2π |
|||||||||||||||
|
|
|
|
|
= |
|
|||||||||||||||||
|
|
|
|
|
|
2π |
|
|
|
|
|
V |
|
2 |
π |
V |
|
2π |
|||||
|
|
|
|
|
|
|
|
|
|
|
π 3 |
|
|
|
2π |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|||
В задачах № 121-150 требуется провести полное исследование указанных функций и построить их графики. Эти вопросы освещены в следующей литературе [1, гл.6, п.8; 2, гл.7, п.2].
При исследовании целесообразно придерживаться следующей схемы:
1)найти область определения функции, вычислить предельные значения на её границе, найти уравнения вертикальных и наклонных асимптот, если они существуют. Найти точки пересечения графика с осями координат;
2)с помощью первой производной найти интервалы возрастания и убывания функции, её экстремумы;
3)с помощью второй производной определить интервалы выпуклости и вогнутости графика функции и точки перегиба.
Рекомендуется построение графика функции проводить поэтапно параллельно с исследованием по указанной схеме.
Пример. Построить график функции y = 3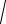 x3 + 3x2 .
x3 + 3x2 .
Решение. 1. Функция определена при всех x (− ∞, ∞) и непрерыв-
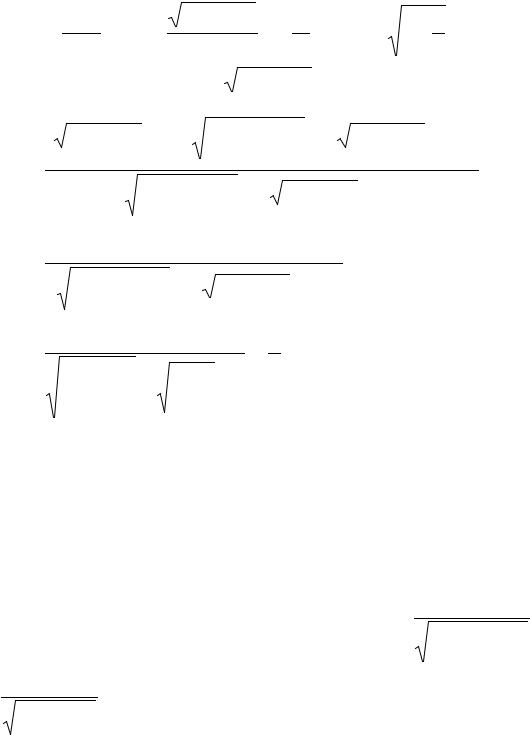
на в области определения, следовательно, нет вертикальных асимптот. Найдём уравнение наклонной асимптоты y = kx +b , где
8
k = lim |
f (x) |
|
|
|
|
|
3 x3 |
+ 3x2 |
∞ |
|
= lim |
3 1 |
+ |
3 |
= 1, |
||||||||||||||||||||||
|
|
|
x |
|
|
= lim |
|
x |
|
= |
|
|
|
x |
|||||||||||||||||||||||
x→±∞ |
|
|
|
) |
|
|
x→±∞ |
|
|
|
∞ |
|
|
|
x→±∞ |
|
|
|
|
|
|||||||||||||||||
x→±∞( |
f |
( |
x |
− kx |
) |
|
x→±∞( |
3 x3 + |
3x2 |
− x |
) |
|
|
{ |
|
|
|
} |
|
|
|
|
|||||||||||||||
b = lim |
|
|
|
|
|
= |
lim |
|
|
= |
|
∞ − ∞ |
|
= |
|
|
|||||||||||||||||||||
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
( |
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
x |
3 |
+ 3x |
2 |
|
|
|
|
x |
3 |
+ 3x |
2 |
|
2 |
+ x |
3 |
|
x |
3 |
+ 3x |
2 |
+ x |
2 |
|
|
|||||||||||
= lim |
|
|
|
|
− x 3 |
|
|
|
|
|
|
|
|
|
|
|
= |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(x3 |
+ 3x2 )2 + x3 |
x3 + 3x2 + x2 |
|
|
|
|
|
|
||||||||||||||||||
x→±∞ |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
x3 + 3x |
2 − x3 |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
(x3 |
+ 3x2 )2 + x3 x3 + 3x2 + x |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
x→±∞ |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
= 3 |
= 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x→±∞ |
|
|
|
|
|
|
|
3 |
2 |
|
|
|
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 + |
|
+ 3 |
1 + |
+ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Получили уравнение наклонной асимптоты y = x +1. Функция пересекает ось ординат при y = 0 и ось абсцисс при x = −3 и x = 0.
Функция не обладает свойствами чётности, нечётности и периодичности.
2. Определим интервалы возрастания и убывания функции и её экстремумы, для чего находим первую производную
|
|
x |
3 |
+ 3x |
2 |
) |
1 |
′ |
= |
1 |
( |
x |
3 |
+ 3x |
2 |
) |
− |
2 |
( |
3x |
2 |
+ 6x |
) |
= |
x2 + 2x |
= |
|
|
|
3 |
|||||||||||||||||||||||||
y′ = |
|
|
3 |
|
|
|
|
|
3 (x3 + 3x2 )2 |
||||||||||||||||||
|
( |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||
= |
x + 2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3 |
( |
|
|
) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x x + 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
y′ = 0 |
при x1 = −2 |
и производная не существует при x2 = −3, x3 = 0 . |
|||||||||||||||||||||||||
Эти критические точки разбивают область определения на интервалы |
||
(− ∞,−3); |
(− 3,−2); |
(− 2,0); (0, ∞). |
Внутри каждого интервала знак производной сохраняется. Чтобы определить знак производной на каждом интервале, выбираем в каждом из них по одной точке и вычисляем значение производной в этих точках. Например, в интервале (− ∞,−3) возьмём точку x = −4 ,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
тогда y′(− 4)= |
− 4 + 2 |
|
|
f 0 , следовательно, функция на интервале |
||||||||||||||||||||
|
|
|
|
3 |
( |
) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
− 4 − |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
(− ∞,−3) возрастает. На интервале (− 3,−2) функция возрастает, так |
||||||||||||||||||||||||
как y′(− 2,5) |
|
= − 2,5 + 2 f 0. На интервале (− 2,0) функция убывает, так |
||||||||||||||||||||||
|
|
|
|
3 |
− 2,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
y′(−1)= |
|
−1 + 2 |
|
|
|
|
|
|
|
|
|
(0, ∞) функция возрастает, так |
||||||||||
как |
|
3 − 4 p 0. |
|
|
На интервале |
|||||||||||||||||||
как |
y′(1)= 1 + 2 f 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
3 16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Составим для наглядности таблицу изменения знаков производной |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x |
(− ∞,−3) |
|
-3 |
(− 3,−2) |
|
|
|
-2 |
|
(− 2,0) |
|
|
0 |
(0, ∞) |
||||||||||
y′ |
|
+ |
|
не суще- |
|
|
|
+ |
|
|
|
0 |
|
- |
|
|
|
|
не суще- |
+ |
||||
|
|
|
|
ствует |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ствует |
|
|||
y |
возрас- |
|
нет экст- |
возрас- |
макси- |
убыва- |
|
|
мини- |
возрас- |
||||||||||||||
|
тает |
|
ремума |
тает |
|
мум |
|
ет |
|
|
мум |
тает |
||||||||||||
ymax (− 2)= 3 |
|
≈ 1,6; |
ymin (0)= 0. |
|
|
|
|
|
|
|
|
|
|
|||||||||||
4 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
3. Определим интервалы выпуклости , вогнутости, точки перегиба |
|||||||||||||||||||||||
графика функции, для чего найдём вторую производную: |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
′ |
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
y′′ = |
(x + 2)(x3 + 3x2 )− |
3 = (x3 + 3x2 )−3 + |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
2 |
|
|
− |
5 |
|
|
|
|
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
3 (3x2 |
+ 6x)= − |
, |
|
||||||||||||
|
|
|
|
|
+ (x + 2) − |
3 |
(x3 + 3x2 ) |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 x4 |
(x + 3)5 |
|
|||||
которая не равна нулю для любого конечного x. Поэтому точками перегиба могут быть те точки, в которых y′′ не существует, то есть
x1 = −3; x2 = 0 . Определим знак второй производной в каждом из ин-
тервалов, на которые найденные критические точки разбивают область определения, и составим таблицу изменения знаков второй производной
