
В.М. Волков Математика и математика в экономике. Программа, контрольные задания и методические указания
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
КУЗБАССКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ
МАТЕМАТИКА И МАТЕМАТИКА В ЭКОНОМИКЕ
Программа, контрольные задания и методические указания для студентов заочной формы обучения специальностей 060400 – «Финансы и кредит»
060500 – «Бухгалтерский учет, анализ и аудит» 060800 – «Экономика и управление на предприятиях» 061000 –«Государственное и муниципальное управление» (сокращенные сроки обучения)
Составители В.М. Волков Е.А. Волкова В.А. Гоголин Е.Н. Грибанов И.А. Ермакова
Утверждено на заседании кафедры Протокол № 1 от 30.08.2000
Рекомендовано к печати учебно-методической комиссией специальности 060500 Протокол №1 от 28.09.2000
Электронная копия находится в библиотеке главного корпуса КузГТУ
Кемерово 2000
1
Введение
Программа, задания контрольных работ и методические указания составлены в соответствии со стандартами Министерства образования РФ и с учетом особенностей программ Кузбасского государственного технического университета для студентов экономических специальностей, обучающихся по ускоренной форме подготовки. Контрольные работы № 1,2,3 выполняются в первом семестре, № 4,5,6 – во втором. Для выполнения контрольных работ необходимо изучить теоретический материал в соответствии с рекомендуемой литературой и ссылкой на источник, которая указана при разборе заданий. Программа курса по математике является также списком теоретических вопросов, предлагаемых на экзаменах.
Выбор своего варианта в каждом задании определяется двумя последними цифрами зачетной книжки – числом десятков и числом единиц. К каждой из этих цифр следует прибавить 1. Таким образом, получаются два числа m и n, задающие значения параметров в каждом задании, соответствующих вашему варианту. Например, если последние цифры 25, то m=3, n=6; если последние цифры 09, то m=1, n=10. На титульном листе выполненных по своему варианту контрольных работ следует указать номер зачетной книжки.
ПРОГРАММА 1 семестр
1. Линейная алгебра и аналитическая геометрия
1.1. Элементы теории определителей
1.2. Системы линейных уравнений
1.3. Формулы Крамера
1.4. Метод Гаусса
1.5. Линейные операции над матрицами
1.6. Умножение матриц. Обратная матрица
1.7. Решение систем линейных уравнений в матричной форме
1.8. Векторы. Линейные операции над ними
1.9. Линейная независимость векторов. Базис
1.10. Уравнения прямой на плоскости
1.11. Графическое решение систем линейных неравенств
1.12. Прямая и плоскость в пространстве
2.Введение в математический анализ. Дифференциальное исчисление
2
2.1. Предел функции
2.2.Бесконечно малые и бесконечно большие функции
2.3.Способы раскрытия неопределенностей
2.4.Непрерывность и точки разрыва функции
2.5.Асимптоты
2.5.Производная
2.6.Дифференциал
2.7.Правила дифференцирования
2.7.Условия монотонности и существования экстремума функции
2.8.Выпуклость, вогнутость и точки перегиба графика функции
2.9.Исследование поведения функций и построение графиков
3.Функции нескольких переменных
3.1. Частные производные
3.2.Частные дифференциалы и полный дифференциал
3.3.Производная по направлению. Градиент
3.4.Экстремумы функций двух переменных
2семестр
4.Интегральное исчисление. Дифференциальные уравнения
4.1.Неопределенный интеграл, его свойства
4.2.Основные методы интегрирования
4.3.Интегрирование дробно-рациональных функций
4.4.Задачи, приводящие к понятию определенного интеграла
4.5.Определенный интеграл, его свойства
4.6.Формула Ньютона-Лейбница
4.7.Геометрические приложения определенного интеграла
4.8.Несобственные интегралы
4.9.Дифференциальные уравнения. Общее и частное решения
4.10.Дифференциальные уравнения первого порядка
4.11.Линейные уравнения второго порядка с постоянными коэффициентами
5.Теория вероятностей
5.1. Алгебра событий
5.2.Классическое определение вероятности
5.3.Вероятность суммы и произведения событий
5.4.Формула Бернулли
5.5.Дискретные случайные величины. Законы распределения
5.6.Непрерывные случайные величины. Законы распределения
5.7.Числовые характеристики случайных величин
3
6. Элементы математической статистики
6.1. Выборочная и генеральная совокупности
6.2.Точечная оценка параметров распределения генеральных совокупностей
6.3.Интервальная оценка параметров распределения
6.4.Критерий согласия Пирсона
6.5.Парная линейная регрессия
6.6.Коэффициент корреляции
Контрольная работа № 1 Линейная алгебра и аналитическая геометрия
1. Проверить систему линейных уравнений на совместность и решить ее двумя методами: а) методом Гаусса; б) по формулам Крамера
[1, c.4-12, c.18-23]. |
|
||||
|
x + |
ny + mz = |
n − m |
||
|
2x + |
|
nz = |
n |
|
|
|
||||
|
3x + ny + mz = 3n − m |
||||
|
|||||
Пример: |
|
|
|
||
|
x − 3y + |
z = |
3 |
|
|
|
2x + |
y − |
3z = |
1 |
|
|
|
||||
|
3x + |
2 y = 6. |
|
||
|
|
||||
Для проверки системы на совместность вычисляем определитель системы, составленный из коэффициентов при неизвестных
|
|
1 |
− 3 |
1 |
|
= 34. Т.к. ∆≠ 0, то система совместна. |
|
|
|||||
∆ = |
|
2 |
1 |
− 3 |
|
|
|
|
3 |
2 |
0 |
|
|
а) Решаем систему методом Гаусса.
Из 2-го уравнения вычтем 1-е уравнение, умноженное на 2. Из 3- го уравнения вычтем 1-е, умноженное на 3. Получим систему
|
x − 3y + z = 3 |
||
|
7 y − |
5z = |
− 5 |
|
|||
|
11y − |
3z = |
− 3. |
|
|||
4
Исключаем y из 3-го уравнения. Для этого 2-е уравнение умножим на 11, 3-е – на 7 и вычтем из 3-го уравнения 2-е. Получим систему
|
x − 3y + |
z = |
3 |
|
7 y − 5z = − |
5 |
|
|
|||
|
34z = |
34. |
|
|
|
||
В обратном порядке находим из 3-го уравнения z = 1, затем из 2- го уравнения y = 0 и из 1-го уравнения х = 2.
Решение системы: x = 2, y = 0, z = 1. б) Решаем систему по формулам Крамера.
Определитель системы ∆ =34. Вычисляем дополнительные определители, полученные заменой каждого из столбцов определителя сис-
темы столбцом правых частей: |
|
|||||||||||||||
|
|
|
3 |
− 3 |
1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|||||||||||
∆ x = |
|
1 |
1 |
− 3 |
|
= 54 + |
2 − 6 + 18 = |
68, |
||||||||
|
|
|
6 |
2 |
0 |
|
|
|
|
|||||||
|
|
|
|
1 |
3 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
∆ y = |
|
2 1 |
− 3 |
|
= − 27 + 12 − 3 + 18 = 0, |
|||||||||||
|
|
|
|
3 |
6 |
|
0 |
|
|
|
|
|
|
|
|
|
∆ z = |
|
1 |
− 3 |
3 |
|
= 6 − 9 + |
12 − 9 − 2 + |
36 = 34. |
||||||||
|
|
|||||||||||||||
|
2 |
1 |
|
1 |
|
|||||||||||
|
|
3 |
2 |
6 |
|
|
|
|
|
|
|
|
||||
Находим решение по формулам Крамера:
|
x = ∆ x / ∆ = 68 / 34 = 2, |
|
y = ∆ y / ∆ = 0 / 34 = 0, |
|
|
|
z = ∆ z / ∆ = 34 / 34 = 1. |
|
2.Элемент aij матрицы А равен номинальному месячному окладу
i- го работника в j – й месяц. Элемент bij матрицы В равен авансу, выдаваемому i – му работнику в j – й месяц. Районный коэффициент равен K. Найти матрицу окончательных выплат С [1, c.12-17].
1 |
+ m / 5 |
1+ n / 5 |
(n + m) / 5 |
|
|
m / 5 |
n / 5 |
m / 5 |
|
|||
|
1 |
+ m / 4 |
1+ n / 4 |
(n + m) / 4 |
|
, |
|
m / 4 |
0 |
n / 4 |
|
, K=1+m/20. |
А = |
|
В = |
|
|||||||||
|
1 |
+ m / 3 |
1+ n / 3 |
(n + m) / 3 |
|
|
|
m / 3 |
n / 3 |
m / 3 |
|
|
|
|
|
|
|
|
|||||||
Пример.
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
3 |
5 |
2 |
|
|
|
1 |
2 |
0 |
|
|
|
|
2 |
4 |
3 |
|
, |
|
0 |
1 |
1 |
|
, |
К=1,3. |
А= |
|
В= |
|
|||||||||
|
4 |
5 |
6 |
|
|
|
2 |
2 |
1 |
|
|
|
|
|
|
|
|
|
|
Матрица окончательных выплат находится из матричного уравнения:
|
|
3 |
5 2 |
|
1 |
2 |
0 |
|
|
1,3 3 − 1 1,3 5 − 2 |
1,3 2 − 0 |
|
|||||
|
|
|
2 |
4 3 |
|
− |
|
0 |
1 |
1 |
|
= |
|
1,3 2 − 0 1,3 4 − 1 |
1,3 3 − 1 |
|
= |
С=КА–В=1,3 |
|
|
|
|
|
||||||||||||
|
|
|
4 |
6 5 |
|
|
|
2 |
2 |
1 |
|
|
|
1,3 4 − 2 1,3 6 − 2 |
1,3 5 − 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2,9 |
4,5 2,6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2,6 |
4,2 2,9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
3,2 |
5,8 5,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3. Заданы матрица прямых затрат А и товарный вектор b для экономической системы из двух предприятий. Определите вектор плана
[1, c.17-18].
A = |
|
M / 20 |
0,35 |
|
|
|
, |
b = |
|
2m + |
3n |
||
|
|
|
|
|
|
|
|
|
|
. |
|||
|
|
0,2 |
|
N / 20 |
|
|
|
|
|
3m + |
|
||
|
|
|
|
|
|
|
|
2m. |
|||||
|
|
Пример. |
|
|
|
|
|
|
|
|
|
||
A = |
|
0,2 |
0,4 |
|
b |
= |
|
11 |
|
|
|
||
|
|
|
, |
|
|
. |
|
|
|
||||
|
|
0,1 |
0,6 |
|
|
|
|
|
19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Находим матрицу |
|
|
|
1 |
0 |
|
|
0,2 |
|
0,4 |
|
|
0,8 |
− 0,4 |
|
||||||||||
Е – А = |
|
|
|
|
− |
|
|
|
= |
|
|
|
. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
|
0,1 |
|
0,6 |
|
|
− 0,1 |
0,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Вычисляем определитель этой матрицы |
|
|
|
|
|
|
|||||||||||||||||||
∆ = |
|
− |
0,8 |
− |
0,4 |
|
= |
0,28. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
0,1 |
|
0,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Строим обратную матрицу |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
( Е – А )-1 |
|
|
1 |
|
0,4 |
0,4 |
|
|
1,43 |
1,43 |
|
|
|
|
|
||||||||||
= |
|
|
|
|
≈ |
|
|
|
|
|
|
. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
0,28 |
|
0,1 |
0,8 |
|
|
0,36 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
2,86 |
|
|
|
|
|
||||||||||||
Находим вектор плана |
|
|
|
|
11 |
|
42,9 |
|
|
|
|
||||||||||||||
X = (E − |
A) |
|
|
|
|
|
|
1,43 1,43 |
|
|
|
|
|
||||||||||||
− 1 b = |
|
|
|
|
|
|
= |
|
|
. |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
0,36 2,86 |
|
|
|
19 |
|
|
58,3 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
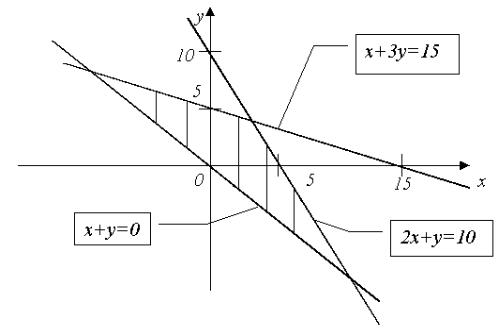
4. Построить на плоскости область, соответствующую системе неравенств [1, c.46-51].
6
|
mx + ny |
|
|
|
≤ mn |
|
|
|
||||
|
( m |
− n )x + ( − 1)n y ≤ m − n |
|
|
||||||||
|
|
|
||||||||||
|
|
n |
|
|
1) |
m |
my ≤ 0 |
|
|
|
||
|
( − 1) x + ( − |
|
|
|
|
|||||||
|
Пример: |
|
|
|
|
|
|
|
|
|||
|
2х + у ≤ |
10 |
|
|
|
|
|
|||||
|
|
х + |
3у ≤ |
15 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||||
|
|
х + |
у ≥ |
0. |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||||
|
Строим прямые, являющиеся границами области: |
|||||||||||
|
2х + у = 10, х + 3у = 15, х + у = 0. |
|||||||||||
|
х 0 5 |
|
|
|
х 0 |
15 |
х |
0 5 |
||||
|
у 10 |
0 |
|
|
|
у 5 |
|
0 |
у |
0 -5 |
||
|
Выделяем части плоскости (полуплоскости), которые соответст- |
|||||||||||
вуют |
знакам неравенств. |
Для этого подставляем координаты произ- |
||||||||||
вольной точки в неравенства и проверяем их знак. Так для точки О(0;0) 1-е и 2-е неравенства выполняются, поэтому все точки плоскости, лежащие по одну сторону от прямых вместе с точкой О являются решением 2-х первых неравенств. Выполнение третьего неравенства нельзя проверить координатами точки О, т.к. получаем 0=0. Выбираем другую точку, например (0;5). Для него 3-е неравенство выполняется. Поэтому соответствующая полуплоскость лежит выше 3-ей прямой. Находим пересечение полуплоскостей и получаем область, соответствующую системе неравенств (на рисунке она заштрихована).
7
Контрольная работа № 2 Введение в математический анализ Дифференциальное исчисление
|
1. Найти пределы [1,68-77]. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
а) |
lim |
|
(m − |
2n)x3 + nx2 + |
(m − n) x |
, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
m + nx − |
(2m − |
n)x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
x→ |
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
б) |
lim |
x3 − |
nx2 − |
( − |
1)m mx + |
( − 1)m nm |
, |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
x2 + ( m − n )x − mn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
x→ |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
в) lim ln(1+ |
( − 1)n |
|
2mxn − |
nxm ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
x→ |
0 |
|
|
|
|
|
nxn + |
mxm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Примеры: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
a) lim |
|
|
2x3 |
− 4x2 + 1 |
= |
|
∞ |
|
2x3 − 4x2 + 1 ~ |
2x3 , 3 |
− 2x − |
x3 ~ − x3 |
= |
|||||||||||||||||||
|
|
|
3 − |
2x − x3 |
|
|
∞ |
= |
||||||||||||||||||||||||
|
x→ |
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= |
lim |
|
2x3 |
= |
− 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
− |
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
x→ |
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
lim |
|
|
|
x2 − 4 |
|
|
|
|
0 |
|
|
lim |
( x |
− 2 )( x + 2 ) |
= lim |
|
x + 2 |
|
4. |
|
|||||||||||
б) |
|
|
|
|
|
|
|
= |
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
= |
|
|||||||
|
|
|
|
|
|
|
|
|
( x |
− 2 )( x − 1) |
|
x − 1 |
|
|||||||||||||||||||
|
x→ |
2 x2 − |
3x − 2 |
|
0 |
|
x→ |
2 |
x→ 2 |
|
|
|
||||||||||||||||||||
в) |
lim |
ln(1 |
− |
x3 ) |
= |
|
0 |
= |
ln(1− x3 ) ~ − |
x3 |
= |
lim |
− |
x3 |
= |
|
− |
lim x = |
0. |
|||||||||||||
|
|
|
x2 |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
x→ |
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
x→ 0 x2 |
|
|
|
x→ 0 |
|
||||||
|
2. Найдите точки разрыва функции. Сделайте чертеж [1, c.77-81]. |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
(− 1)m mx2 , x ≤ 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
y = |
|
(− 1)n nx + (− 1)n + (− 1)m ,0 " x ≤ m, |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
(− |
1) |
m |
/(m − x), x ! m. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
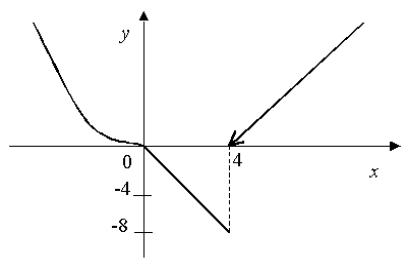
Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
3x2 ,x ≤ 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
y = |
|
− 2x,0 " x ≤ 4; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
x |
− |
4,x ! 4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
8
На интервалах (–∞ ;0), (0;4), (4;+∞ ) функция непрерывна. Исследуем поведение функции в точках х=0 и х=4.
lim |
y = |
lim |
3x2 = |
0 = y( 0 ). lim |
y = |
lim − |
2x = |
0. |
||
x→ 0− 0 |
|
x→ 0− 0 |
|
x→ |
0+ 0 |
x→ |
0+ 0 |
|
|
|
В точке х=0 функция непрерывна. |
|
|
|
|
|
|
||||
lim |
y = |
lim |
− 2x = |
− 8 = y( 4 ). |
lim |
y = |
lim |
x − |
4 = 0. |
|
x→ 4− 0 |
|
x→ 4− 0 |
|
|
x→ |
4+ 0 |
|
x→ 4+ 0 |
|
|
В точке х=4 функция имеет разрыв 1-го рода.
3.Исследуйте поведение функций и постройте их графики [1, c. 81-
100].
|
а) |
y = ( − 1)n xn+ 2 + ( − 1)m( n + 2 )xк / k + ( n − m ), |
|
|
|||||||||
|
|
|
1 |
|
( − 1)m + ( − 1)n |
|
|
|
|||||
|
|
|
|
|
|
|
|||||||
|
k = |
1+ |
|
|
, |
|
|
||||||
|
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) y = ( − 1)m x2 + n . |
|
|
|
|||||||||
|
|
|
|
( − 1)n xк − |
m |
|
|
|
|||||
|
Примеры: а) у=5х4-4х5+1. |
|
|
||||||||||
Область определения функции (–∞ ;+∞ ). |
|
|
|||||||||||
lim y = |
|
lim ( 5x4 − 4x5 + 1) = |
lim ( − 4x5 ) = #∞ . |
|
|
||||||||
x→ |
±∞ |
x→ |
±∞ |
|
|
x→ ±∞ |
|
|
|||||
Функция непрерывна. Вертикальных асимптот нет. |
|
|
|||||||||||
Находим наклонные асимптоты у=kх+b. |
|
|
|||||||||||
k = |
lim |
y |
= |
lim |
5x4 − |
4x5 + 1 |
= |
lim ( 5x3 − 4x4 + 1/ x ) = |
lim − |
4x4 = −∞ . |
|||
|
|
|
|||||||||||
|
x→ ∞ |
x |
x→ ∞ |
x |
x→ ∞ |
x→ ∞ |
|
||||||
|
Следовательно, наклонных асимптот нет. |
|
|
||||||||||
|
Устанавливаем |
области |
монотонности и находим |
экстремумы |
|||||||||

9
функции:
у′=20х3-20х4=0, х3-х4=0, х3(1-х)=0.
х1=0, х2=1 – критические точки на экстремум.
Определяем знаки производной на интервалах и соответственно области монотонности:
Т.о. ymin( 0 ) = 1, ymax(1) = 2.
Исследуем график функции на выпуклость, вогнутость и находим точки перегиба: y′′=(20x3–20x4)′=60x2–80x3=0,
3х2 – 4х3 = 0; х1 = 0, х2 = 3/4 – критические точки на перегиб. Определяем знаки второй производной на интервалах, а по ним -
области выпуклости и вогнутости графика: Т.о. х2 =3/4 – точка перегиба, у(3/4) = 1,6.
Составляем таблицу характерных точек функции и по ней строим ее график:
х |
-∞ |
0 |
3/4 |
1 |
+∞ |
у |
+∞ |
1 |
1,6 |
2 |
-∞ |
• |
|
y |
|
|
|
|
|
|
(+∞ ) |
|
|
|
|
||
|
|
|
|
|
|
||
|
|
2 |
• |
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
• |
|
|
|
|
(– ∞ |
) |
0 |
3/4 |
1 |
(+∞ |
) |
x |
|
|
|
|
|
|
||
|
|
(– ∞ |
) |
|
|
|
• |
|
|
|
|
|
|
|
|
