В.М. Волков Математика и математика в экономике. Программа, контрольные работы №4, 5, 6 и методические указания для студентов 2 курса заочной формы обучения

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

КУЗБАССКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра прикладной математики

МАТЕМАТИКА И МАТЕМАТИКА В ЭКОНОМИКЕ

Программа, контрольные работы № 4,5,6 и методические указания для студентов 2 курса заочной формы обучения специальностей 060400, 060500, 060800

Составитель В.М.Волков

Утверждены на заседании кафедры Протокол № 5 от 06. 04. 01

Рекомендованы к печати учебнометодической комиссией специальности 060400 Протокол № 3 от 19. 04. 01

Электронная копия находится в библиотеке главного корпуса КузГТУ

Кемерово 2001

1

Контрольные работы № 4,5,6 составлены в соответствии с программой курса высшей математики для студентов-заочников инженерно- экономических специальностей. В составлении работ и методических указаний к ним принимали участие преподаватели: В.М.Волков, Е.А.Волкова, О.С.Георгинская, В.А.Гоголин, И.А.Ермакова.

Номера задач контрольных работ студент должен выбрать по таблице «Выбор номеров контрольных задач» следующим образом:

найти строку, соответствующую первой букве фамилии; найти столбец, соответствующий последней цифре шифра зачётной книжки;

на пересечении найденных строки и столбца взять номера задач контрольных работ № 4,5,6.

Контрольные работы, выполненные не по своему варианту, возврааются непроверенными.

ПРОГРАММА курса «Высшая математика» для инженерно-

экономических специальностей (2 курс)

1. Функции нескольких переменных

1.1.Понятие функции нескольких переменных. Областьопределения. Непрерывность.

1.2.Частные производные первого порядка. Полный дифференциал функции, его применение к приближённым вычислениям.

1.3.Касательная плоскость к поверхности. Частные производные высших порядков.

1.4.Экстремум функции двух переменных. Наибольшее и наименьшее значения функции двух переменных.

1.5.Градиент. Производная функции двух переменных по направле-

нию.

2. Неопределённый интеграл

2.1.Первообразная (неопределённый интеграл), её свойства. Таблица интегралов.

2.2.Непосредственное интегрирование. Интегрирование по частям и подстановкой.

2.3.Использование таблиц (справочников) неопределённых инте-

гралов.

3. Определённый интеграл

2

Выбор номеров задач контрольных работ

3

3.1.Задачи, приводящиеся к понятию определённого интеграла.

3.2.Определённый интеграл как предел интегральных сумм.

3.3.Основные свойства определённого интеграла.

3.4.Производная интеграла по переменному верхнему пределу. Формула Ньютона-Лейбница.

3.5.Приложение определённого интеграла к вычислению площадей плоских фигур, длин дуг кривых, объёмов тел вращения.

4.Криволинейные интегралы

4.1.Задачи, приводящиеся к криволинейным интегралам.

4.2.Определение криволинейных интегралов по длине дуги и по координатам, их основные свойства и вычисление.

4.3.Приложение интегралов к вычислению масс неоднородных линий и работы переменной силы.

5.Обыкновенные дифференциальные уравнения

5.1.Задачи, приводящиеся к дифференциальным уравнениям. Основные определения.

5.2.Дифференциальные уравнения первого порядка. Задача Коши. Теорема существования и единственности решения задачи Коши.

5.3.Интегрирование простейших типов дифференциальных уравнений: с разделяющимися переменными, однородных и линейных.

5.4.Дифференциальные уравнения второго порядка. Задача Коши. Уравнения, допускающие понижение порядка.

5.5.Линейные дифференциальные уравнения с постоянными коэффициентами.

5.6.Применение дифференциальных уравнений для решения задач физики и механики.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К КОНТРОЛЬНЫМ РАБОТАМ

Контрольная работа №4

Для решения данной контрольной работы следует проработать литературу по теме «Функции нескольких переменных» [2, гл. IX, с. 4- 24, с. 31-38, с. 41-44; 6, гл. I, с. 9-16, гл. YI, с. 248-251; 7, гл. YIII, с. 208221].

4

При решении задач 1-30, если функция двух переменных задана только аналитическим выражением, то под областью определения понимают совокупность всех точек плоскости OXY, в которых аналитическое выражение определено и принимает действительные значения. Например, для функций z = ϕ(x,y), где ϕ(x,y) - некоторая функция двух

переменных, выполнены условия:

1)z = (a ) область определения D : ϕ(x,y)≠ 0 ;

ϕx,y

2)z = 2n ϕ(x,y) область определения D : ϕ(x,y)≥ 0,n f0 - целое;

3)z = lnϕ(x,y) область определения D : ϕ(x,y)f0 ;

4)z = arcsinϕ(x,y) область определения D : ϕ(x,y)≤1 .

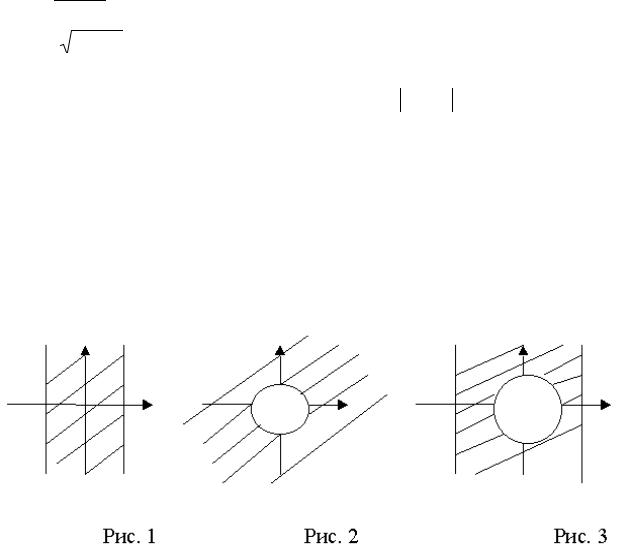
Областью определения первого слагаемого является часть плоскости, выделенная штриховкой на рис.1.

Второе слагаемое определено при x2 + y2 −1 f0 x2 + y2 f1. Изобра-

зим штриховкой область определения второго слагаемого на чертеже

(рис. 2).

Область определения нашей функции есть пересечение областей определения слагаемых функции (рис. 3). Точки линий x = −2, x = 2 при-

надлежат области определения, а точки окружности x2+y2 =1 не принадлежат области определения.

5

Для решения задач 31-60 нужно уметь находить частные производные первого и второго порядка [2, гл. IX, с. 1217; 6, гл. YI, с. 253256; 7, гл. YIII, с. 209210].

Пример. Показать, что функция z = x2 sin yx удовлетворяет уравне-

нию ∂2z = ∂2z .

∂x∂y ∂y∂x

Решение. Найдём частные производные функции z = x2 sin yx перво-

го порядка. Рассматривая y как постоянную величину, получим частную производную функции z по x :

Рассматривая x как постоянную величину, получим частную производную функции z по y :

Найдём вторые частные производные:

Подставим частные производные второго порядка в заданное уравнение

cos yx + yx sin yx = cos yx + yx sin yx .

Получили тождество, то есть функция z удовлетворяет заданному уравнению.

При решении задач 61-90 во втором пункте нужно использовать приложения полного дифференциала к приближённым вычислениям

[2, гл. IX, с. 2021; 6, гл. YI, с. 264-266; 7, гл. YIII, с. 219221].

6

Пример. Дана функция z = x2 + xy − y и две точки A(1,2) и B(1,03;1,98). Требуется: 1) вычислить значение z1 в точке B; 2) вычислить приближённое значение z1 функции в точке B, исходя из значения z0 функ-

ции в точке A и заменив приращение функции при переходе от точки A к точке B дифференциалом; 3) оценить в процентах относительную погрешность, получающуюся при замене приращения функции её дифференциалом; 4) составить уравнение касательной плоскости к поверхно-

сти z = x2 + xy − y в точке C(1,2,z0 ).

Решение. 1. z1 = z(B)= (1,03)2 +1,03 1,98 −1,98 =1,1203 .

2. Используем формулу

f (x0 + ∆x,y0 + ∆y)≈ f (x0 ,y0 )+ fx′(x0 ,y0 )∆x + fy′(x0 ,y0 )∆y . Положим x0 =1, x0 + ∆x =1,03, y0 = 2, y0 + ∆y =1,98. Тогда

∆x = 0,03; ∆y = −0,02 .

Для заданной функции вычисляем частные производные

f (x0 ,y0 )= f (1,2)= z0 =1 + 2 − 2 =1.

Следовательно:

z1 = f (x0 ,y0 )+ fx′(x0 ,y0 )∆x + fy′(x0 ,y0 )∆y =1 + 4 0,03 + 0 (− 0,02)=1,12 .

3. Относительную погрешность определяем по формуле

4. Используем уравнение касательной плоскости:

fx′(x0 ,y0 )(x − x0 )+ fy′(x0 ,y0 )(y − y0 )− (z − z0 )= 0

к поверхности z = f (x,y). Подставляем в уравнение касательной плоско-

сти все данные, найденные в п. 2, получим

4(x −1)+ 0(y − 2)− (z −1)= 0 или 4x − z − 3 = 0 .

Для решения задач 91 –120 следует знать, что функция, непрерывная в ограниченной замкнутой области, достигает наибольшего и наименьшего значений или в критических точках, лежащих внутри, или на границе области, или в угловых точках границы области [2, гл. IX, с. 4147; 6, гл. YI, с. 266-275; 7, гл. YIII, с. 221-225].

7

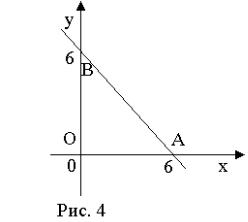
Пример. Функция z = x2 − 2xy − y2 + 4y задана в треугольнике, ограниченном прямыми x = 0; y = 0; x + y = 6 .Найти наибольшее и наимень-

шее значения функции z .

Решение. Построим заданную область (рис. 4). Найдём критические точки внутри области, пользуясь необходимым условием существова-

ния экстремума z′x = 0,

z′y = 0.

z′x = 2x − 2y,

z′y = −2x − 2y + 4.

Решаем систему двух уравнений с двумя неизвестными

которая лежит внутри области. Значение функции в этой точке z1 =1 − 2 −1 + 4 = 2. Исследуем функцию

z = x2 − 2x 0 − 0 + 4 0 = x2 , то есть является функцией одной переменной. Определим критические точки z′x = 2x, 2x = 0, x = 0 . Получаем точку

является функцией одной переменной. Определим критические точки

лежит отрезку, вычисляем z4 = z(M3 )= −14 . Найдём значения функции в угловых точках A(6,0); B(0,6) (в точке О значение уже вычислено).

z5 = z(A)= 36 − 0 − 0 + 0 = 36, z6 = z(B)= 0 − 0 − 36 + 24 = −12 .

Из полученных значений z1 = 2,z2 = 0,z3 = 4,z4 = −14,z5 = 36,z6 = −12 выбираем наибольшее и наименьшее. Получаем

8

zнаиб = z(A)= 36, zнаим = z(M3 )= −14 .

При решении задач 121 –150 нужно использовать понятия скалярного поля, производной по заданному направлению и градиента функции

[2, гл. IX, с. 3138; 6, гл. YIII, с. 343-348].

Например, для определения градиента функции z = 5x2y − 7xy2 + 5xy в точке A(1,2) нужно найти значения частных производных в этой точке.

Для нахождения производной в точке А по направлению вектора a = −2 ri + rj найдём направляющие косинусы вектора a = −2 ri + rj

Согласно определению производной функции вдоль заданного направ-

Контрольная работа №5

Для вычисления неопределённых интегралов № 1-30 необходимо проработать литературу: [1, гл.7, с. 285-312; 3, гл.5, с. 253-286; 6, гл.4,

с. 154-183; 7, гл.9, с. 225-286], где содержатся практические рекомендации по данной теме.

Для выполнения задания 1-30 (пункт а) нужно из таблицы интегралов выбрать такой, к которому можно свести данный интеграл.

9

Например, при вычислении

Согласно этой формуле подводим под знак дифференциала основание степени. Так как d(5x + 2)= 5dx, то умножим и разделим интеграл на 5,

то есть

При вычислении интегралов в пункте б применяются методы под-