Добавил:

fench Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Кузбасский государственный технический университет

Предмет:

Высшая математика

Файл:

В.М. Волков Математика. Контрольные работы №1, 2, 3 и методические указания к ним для студентов-заочников инженерно-технических спецальностей

.pdf

Скачиваний:

230

Добавлен:

19.08.2013

Размер:

411.8 Кб

Скачать

☆

1 / 51 2 3 4 5 > Следующая >>>

Министерство образования Российской Федерации Государственное учреждение

Кузбасский государственный технический университет

Кафедра прикладной математики

МАТЕМАТИКА

Контрольные работы №1, 2, 3 и методические указания к ним для сту- дентов-заочников инженерно-технических специальностей

Составители В. М. Волков Е. А. Волкова В. А. Гоголин Е.Н. Грибанов Т.И. Кургузкина Е. В. Прейс

Утверждены на заседании кафедры

Протокол № 5 от 04.03.02

Рекомендованы к печати учебно-методической комиссией специальности 090200 Протокол № 11 от 29.03.02

Электронная копия хранится в библиотеке главного корпуса ГУ КузГТУ

Кемерово 2002

ВВЕДЕНИЕ

Данные контрольные работы составлены в соответствии с методическими указаниями по математике, разработанными учебнометодическим управлением по высшему образованию, и с учетом особенностей учебных программ специальностей, по которым обучаются в ГУ Кузбасский государственный технический университет. Контрольные работы №1, 2, 3 выполняют в первом семестре. Номера задач контрольной работы определяют по табл. 1. В первом столбце студент находит первую букву своей фамилии, в первой строке таблицы отмечает последнюю цифру шифра своей зачетной книжки и берет номера, находящиеся на пересечении строки (с первой буквой фамилии) и столбца (с последней цифрой шифра). Например, студент А.И.Петров имеет шифр зачетной книжки 82-458. Буква “ П “ находится в шестой строке, последняя цифра “8” попадает в девятый столбец, на их пересечении записаны номера 29, 39, 78, 106 и 136. Студент А.И. Петров в каждой контрольной работе выполняет задания под данными номерами.

ПРОГРАММА

1.ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ

ИАНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ

1.Определители второго и третьего порядков, их свойства. Определители n-го порядка. Метод Крамера решения систем линейных урав-

нений.

2.Векторы. Линейные операции над векторами. Проекция вектора на ось. Направляющие косинусы и длина вектора.

3.Скалярное произведение и его свойства. Длина вектора и угол между двумя векторами в координатной форме. Условие ортогональности двух векторов. Механический смысл скалярного произведения.

4.Векторное произведение двух векторов и его свойства. Условие коллинеарности двух векторов.

5.Смешанное произведение векторов. Геометрический смысл.

6.Уравнения линий на плоскости. Различные формы уравнения прямой на плоскости. Угол между прямыми. Расстояние от точки до прямой.

Выбор номеров задач контрольных работ

Начальная					Последняя цифра шифра
буква	0	1	2	3		4	5	6	7	8	9
фамилии	0	1	2	3		4	5	6	7	8	9
фамилии
А В Д	1, 31, 80,	2,32,79,	3,33,78,	4,34,76,		5,35,76,	6,36,75,	7,37,74,	8,38,73,	9,39,72,	10,40,71,
А В Д	110, 130	100,150	101,131	120,130		91,141	110,140	111,121	100,150	101,131	120,130
Б Е З	11,41,70,	12,42,69,	13,43,68,	14,44,67,		15,45,66,	16,46,65,	17,47,64,	18,48,63,	19,49,62,	20,50,61,
Б Е З	109,129	99,149	102,132	119,129		92,142	109,139	112,122	99,149	102,132	119,129
Г Ж И Л	21,51,80,	22,52,79,	23,53,78,	24,54,77,		25,55,76,	26,56,75,	27,57,74,	28,58,73,	29,59,72,	30,60,71,
Г Ж И Л	108,128	98,148	103,133	118,128		93,143	108,138	113,123	98,148	103,133	118,128
К	1,60,90,	2,59,89,	3,58,88,	4,57,87,		5,56,86,	6,55,85,	7,54,84,	8,53,83,	9,52,82,	10,51,81,
К	107,127	97,147	104,134	117,127		94,144	107,137	114,124	97,147	104,144	117,127
	107,127	97,147	104,134	117,127		94,144	107,137	114,124	97,147	104,144	117,127
М Н О	11,49,70,	12,48,61,	13,47,62,	14,46,63,		15,45,64,	16,44,65,	17,43,66,	18,42,67,	19,41,68,	20,42,69,
М Н О	106,126	96,148	105,135	116,126		95,145	106,136	115,125	96,146	105,135	116,126
П Ы	21,31,80,	22,32,71,	23,33,72,	24,34,73,		25,35,74,	26,36,75,	27,37,76,	28,38,77,	29,39,79,	30,40,79,
	105,125	95,145	106,136	115,125		96,146	105,135	116,126	95,145	106,136	115,125
С У Е	1,60,90,	2,59,81,	3,58,82,	4,57,83,		5,56,84,	6,55,85,	7,54,86,	8,53,87,	9,52,88,	10,51,89,
С У Е	104,124	94,144	107,137	114,124		97,147	104,134	117,127	94,144	107,137	114,124
Р Т Ф	11,50,70,	12,49,61,	13,48,62,	14,47,63,		15,46,64,	16,45,65,	17,44,66,	18,43,67,	19,42,68,	20,41,69,
Р Т Ф	103,123	93,143	108,138	113,123		98,148	103,133	118,128	93,143	108,138	113,123
Х Ц Ш	21,40,80,	22,39,71,	28,38,72,	24,37,73,		25,36,74,	26,35,75,	27,34,76,	28,33,77,	29,32,78,	30,31,79,
Х Ц Ш	102,122	92,142	109,139	112,122		99,149	102,132	119,129	92,142	108,139	112,122
Ч Щ Э	1,51,90,	2,52,81,	3,53,82,	4,54,83,		5,55,84,	6,56,85,	7,57,86,	8,58,87,	9,59,88,	10,60,89,
Ю Я	101,121	91,141	110,140	111,121		100,150	101,131	120,130	91,141	110,140	111,121

7.Кривые второго порядка, их геометрические свойства и канонические уравнения.

8.Уравнения плоскости и прямой в пространстве. Угол между плоскостями. Угол между прямыми. Угол между прямой и плоскостью.

9.Полярные координаты на плоскости.

2.ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ.

1.Функция. Область ее определения. Способы задания. Основные элементарные функции, их свойства и графики.

2.Числовые последовательности. Предел числовой последовательности. Существование предела монотонной ограниченной последовательности.

3.Предел функции в точке. Предел функции на бесконечности.

4.Непрерывность функции в точке.

5.Бесконечно малые и их свойства. Сравнение бесконечно малых.

6.Точки разрыва.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ

КОНТРОЛЬНАЯ РАБОТА №1

В первую контрольную работу включены задачи по линейной и векторной алгебре, аналитической геометрии. По каждому разделу изучаемых тем даются ссылки с указанием страниц. Ссылки даны на несколько учебников, пользоваться можно любым из них. Приведены рекомендации по преодолению наибольших трудностей, которые встречаются при решении задач.

1. При решении задач №1-60 необходимо использовать знания линейной алгебры [1, гл.5, п 2-3].

x + 3y - z = 2

Для системы линейных уравнений 2x + 4z =1

x + y + 3z = 3

определитель, составленный из коэффициентов при неизвестных, равен:

	1	3	−1	=1	0	4	-3	2	4	+(-1)	2	0	=1(0-4)-3(6-4)-1(2-0)=-12


∆ =	2	0	4
	1	1	3		1	3		1	3		1	1
	1	1	3

[2, гл.3, п 1, с. 69-72]. Так как определитель системы отличен от нуля, то для ее решения можно воспользоваться формулами Крамера [2, гл.3, п 2, с. 78-81; 5, с. 138-141]. Получим решение системы:

			2	3	−1																1		2	−1
			2	3	−1																1		2	−1
			1	0	4																2		1	4
x=	∆x	=	3 1 3			= −	18	= −1,5			;				y =		∆y			=	1 3			3	=	−18	=1,5	;

	∆			−12			12											∆					−12			−12
	∆			−12			12											∆					−12			−12
												1	3		2
												1	3		2
												2	0		1
							z =		∆z	=		1	1		3	=			−	12	=1 .

									∆			−12							−	12
									∆			−12							−	12
									x1 + x2 + x3 − 2x4 =1 ,
	Для решения системы								x		1	− x	2	− 2x			4		= −1			,
									x			+ 5x		2	+ 3x				3	− 2x		4	=	5 ,
											1			2					3			4

у которой число уравнений не равно числу неизвестных, удобнее применить метод Гаусса [3, гл. 2, п 7, с.83-88; 4, с. 23-25; 6, с. 101104]. Приведем систему к треугольному виду. Можно записывать только матрицу коэффициентов:

1	1	1	−2 1	1	1	1	− 2 1		1	1	1	− 2 1
1	−1 0		−2 −1 ~ 0		− 2 −1		0	− 2 ~ 0		− 2 −1		0	− 2 .
1	5	3	−2 5	0	4	2	0	4	0	0	0	0	0

Последняя матрица соответствует системе двух уравнений с четырьмя

неизвестными:	x1 + x2 + x3 − 2x4 =1 ,
	− 2x2 − x3 = −2 .

Примем за свободные неизвестные x3 и x4 , перенесем их в правую часть уравнения и получим общее решение системы:

	x2 =1 − 1 x3	,
	2
x1	=1 + 2x4 − x3 − x2	= 2x4	−	x3	.

Придавая x3 и x4			2
	разные значения, получим множество реше-

ний системы. Теория исследования систем m линейных уравнений с n

неизвестными изложена в [3, гл. 2, п 7; 5, с. 181-190; 6, с.97-100].

2. Для решения задач № 61-90 необходимо проработать литературу: [3, гл.2, п.4, 4, с. 39, задача 4; 6, с.155-161].

Например, векторы a ={1, 2, 3}, b ={0, 4, 5}, c={6, 7, 8} образуют базис в трехмерном пространстве, потому что определитель, со-

ставленный из их координат:	1	0	6	= −15 , отличен от нуля. Любой
ставленный из их координат:	2	4	7	= −15 , отличен от нуля. Любой
	3	5	8

вектор этого пространства можно выразить через данные векторы a , b ,

c . Разложим вектор e = {−1, − 2, − 6} в базисе a, b, с: e = λ1 a + λ2 b + λ3 c . Это равенство векторов равносильно системе трех уравнений с тремя

неизвестными λ1 , λ2 , λ3 :

−1 =1λ1 + 0λ2 + 6λ3 ,− 2 = 2λ1 + 4λ2 + 7λ3 ,− 6 = 3λ1 + 5λ2 + 8λ3 .

Решение системы, которое может быть найдено по формулам Краме-

ра, λ1	= −5,8, λ2	=1, λ3 = 0,8 и есть координаты вектора e в бази-
се a,	b, с, т.е.	e = −5,8a + b + 0,8c .

3. В задачах № 91-120 в пункте первом нужно найти длину ребра Α1 Α2 . Ее следует определять как длину вектора [2, с. 90, 5, с.102, 6,

с.47].		Α1 (1, 2, 3), Α2 (4, 6, 8).
Пусть известны координаты точек		Α1 (1, 2, 3), Α2 (4, 6, 8).
Найдем координаты вектора	Α1 Α2 ={3,	4, 5}. Тогда его длина
Α1 Α2 = 32	+ 42 + 52 =	50 = 7,07 .

При определении угла между ребрами Α1 Α2 и Α1 Α4 (пункт 2) нужно воспользоваться понятием скалярного произведения векторов

[3, гл.2, п.5, п.3; 2, с.96; 5, с. 99] и определить угол

между векто-

рами Α1 Α2 и

Α1 Α4 , имеющими общее начало. Например,

даны три

вершины Α1 (1, 2,

3), Α2 (4,

8),

Α4 (−1, 9

0).

Определим

координаты

векторов

Α1 Α2 ={3, 4, 5},

Α1 Α4 ={− 2, 7, 3}.

Косинус угла α между векторами:

cos α =

Α1 Α2

Α1 Α4

3(−2) + 4 7 + 5(−3)

= 0,126 .

Α1 Α2

Α1 Α4

(−2)2

+ 72 + (−3)2

7,07

7,87

α = arccos 0,126 ≈ 830 .

Углом между ребром

Α1 Α4

и гранью Α1 Α2 Α3

(пункт 3) являет-

ся угол ϕ

между вектором

Α1 Α4

и его проекцией на плоскость

Α1 Α2 Α3 (рис.1).

Угол ϕ

следует находить через угол α

(α = 900 −ϕ),

образованный

вектором

Α1 Α4

и вектором нормали

N к грани

А1 А2 А3 . Так как вектор N перпендикулярен векторам Α1 Α3

и Α1 Α2 ,

то N = Α1 Α3 Α1 Α2 , и для

его определения

необходимо изучить тему

“ Векторное

произведение “ [3, гл. 2, п.5, п.5].

Например,	даны	Α1 (1, 2, 3),
Α2 (4, 6, 8),	Α3 (− 5, − 7, − 2),
Α4 (−1, 9, 0).	Координаты	векторов

	Α1 Α4		={− 2, 7, − 3},				Α1 Α2 ={3, 4, 5},
	Α1 Α3		={− 6, − 9,			− 5}.	Тогда
			i	j	k

N = Α1 Α2 × Α1 Α3 =			3	4	5	= 25i −15 j − 3k ,
		− 6		− 9	− 5

cos α =	(- 2)25 + 7(−15) + (−3)(−3)							= −0,634
	(− 2)2 + 72 + (− 3)2			252	+ (−15)2 + (− 3)2
Следовательно,	α ≈1290 и ϕ ≈ 900			−1290	= −390 .

В п. 4 при определении площади грани Α1 Α2 Α3 нужно использовать

геометрический смысл векторного произведения [1, с. 100, 2, с.51-52, 3, с.136, 7, с.189].

Α1

Α2Α3

В нашем примере

Α1 Α2 ={3,

5}, Α1

Α3 ={− 6, − 9, − 5}

Α1 Α2 × Α1 Α3

={25,

−15,

− 3}.

Тогда

Α1 Α2 × Α1 Α3

= 252 + (−15)2 + (− 3)2

≈ 29,2 ,

SΑ1Α2Α3 ≈14,6.

Для определения объема пирамиды (п.5) следует изучить тему “Смешанное произведение этих векторов “ [2, гл.3, п.3, с.102-103; 6, с.5253; 7, с.194].

Возьмем векторы Α1 Α2 ={3, 4, 5}, Α1 Α3 ={− 6, − 9, − 5},

Α1 Α4 ={− 2, 7, − 3}.

Составим смешанное произведение этих векторов

	3	4	5
Α1 Α2 Α1 Α3 Α1 Α4 =	− 6	− 9	− 5	= −146 ≠ 0
	− 2	7	− 3

Объем пирамиды, построенной на этих векторах, равен

V =	1	Α1 Α2 Α1 Α3 Α1 Α4	V =		−146	≈ 24,3 .



	6			6
	6			6

При решении задач № 91-120 п. 6,7,8 используют некоторые разделы аналитической геометрии.

Так, при составлении уравнения прямой Α1 Α2 используют кано-

нические уравнения прямой в пространстве, проходящей через две данные точки [2, гл.4, п.2, с.142; 5, с.117, 119; 6, с.62; 7, с.228].

Например, пусть Α1 (1, 2,

2), Α2 (4, 6,

8), тогда уравнение пря-

мой Α1 Α2 будет иметь вид

x - 1

y − 2

z − 3

или

x −1

y − 2

z −

4 - 1

6 − 2 8 − 3

Составляя уравнение плоскости Α1 Α2 Α3 , используем формулу уравнения плоскости, проходящей через данную точку М0 (x0 y0 z0 )

перпендикулярно данному вектору:

N ={A, В, С}: A(x - x0 )+ B(y − y0 )+ C(z − z0 )= 0 .

Это рассмотрено в [2, с.130-131; 5, с. 107-111; 7, с.199, 200, 205].

Причем за точку М0

можно взять любую из точек Α1 , Α2 , Α3 .

Мы

возьмем Α1 (1, 2,

3).

Вектор

N ={25,

−15,

− 3}

найден выше

(см.

п.3).

Α1 Α2 Α3 имеет вид

25(x - 1)−15(y − 2)− 3(z − 3)= 0

Уравнение плоскости

или

25x −15 y − 3z +14 = 0.

Для составления уравнения высоты, опущенной из

вершины Α4 на грань Α1 Α2 Α3 , необходимо исполь-

зовать канонические уравнения прямой в про-

странстве

x - x0

y − y0

z − z0

, проходящей через

точку

M0 (x0 ,

y0 ,

z0 ),

параллельно

вектору

S ={m,

p} [3, гл. 4, п.2, 4].

В нашем случае вместо точки

Μ0 возьмем точку А4 ,

а вместо S

возьмем вектор N , т.к. S и

N коллинеарны.

Уравнение высоты имеет вид

x +1

y − 9

−15

− 3

3. Для решения задач № 131-140 необходимо знать, что работа,

совершаемая равнодействующей F

двух постоянных сил

при перемещении тела на прямолинейном участке AB ,

равна скаляр-

ному

произведению вектора силы

на вектор перемещения

AB.

Например,

сила

F1 = i − 2 j + 3k,

F2 = 4i + 5 j − 6k ,

точки

A(0, −1, − 4), B(7, 8, 9).

= 5i + 3 j − 3k , вектор AB ={7,

13}.

Равнодействующая

F = F1 + F2

Вычисляем работу:

A = F AB = 5 7 + 3 9 + (− 3)13 = 23.

В задачах № 121-130 момент равнодействующей F двух сил,

приложенных в точке A относительно точки B ,

нужно находить как

векторное произведение

AB × F [2, гл. 3, п. 3, с. 96, 100; 6, с. 51-52].

Пусть F1 = −i + 3 j − 4k,

= 2i + 8k , точки A(2, 5,

− 8),

B(4,

− 3).

Тогда

F = F1 + F2 = i + 3 j + 4k,

AB ={− 6,

− 5,

5}.

Определяем момент силы F относительно точки B :

Μ = momB F = AB × F =	i	j	k	= i	− 5	5	− j	− 6	5	+ k	− 6	− 5
	i	j	k
	− 6	− 5	5										=
	1	3	4		3	4		1	4		1	3
	1	3	4

= −35i + 29 j −13k.

Величина (модуль) этого вектора Μ = 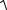(− 35)2 + 292 + (−13)2 = 47,3 . Определяем направляющие косинусы вектора Μ :

cos α =	− 35	= −0,74	cos β =	29	= 0,614	cos γ =	−13	= −0,275 .
	47,3			47,3			47,3

В задачах №141-145 линейную скорость V нужно определять с помощью векторного произведения. Например, угловая скорость ω = 3j , точка A(4, 0, − 7), O(0, 0, 0) - начало координат. Опреде-

ляем вектор OA ={4,				0, − 7}, тогда линейная скорость
	i	j	k
	i	j	k
V =ω ×OA =	0	3	0	= −21i −12k.
	4	0	− 7

При решении задач № 146-150 следует воспользоваться следующей теоремой: для компланарности трех векторов a, b, c необхо-

димо и достаточно, чтобы их смешанное произведение равнялось нулю:

a ×b ×c = 0.

Контрольная работа №2 В контрольную работу № 2 включены задачи на построение ли-

ний и областей на плоскости. Линии и границы областей задаются в декартовых и полярных координатах.

1 / 51 2 3 4 5 > Следующая >>>

Соседние файлы в предмете Высшая математика