
Е.А. Волкова Теория вероятностей иматематическая статистика. Программа, методические указания и контрольные работы №7, 8 для студентов экономических специальностейзаочной формы обучения
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
КУЗБАССКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КАФЕДРА ПРИКЛАДНОЙ МАТЕМАТИКИ
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
И
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Программа, методические указания и контрольные работы №7, 8 для студентов экономических специальностей
заочной формы обучения
Составители: Е.А.Волкова О.С.Георгинская И.А.Ермакова Э.Ф.Золотарева О.А.Зубанова Л.Е.Мякишева Е.В.Прейс Т.К.Скадина
Утверждено на заседании кафедры Протокол № 4 от 23.11.99 Рекомендовано к печати учебно-методической комиссией специальности 060500 Протокол №3 от 17.04.2000 Электронная копия находится в
библиотеке главного корпуса КузГТУ
Кемерово 2000
1
Введение
Настоящее пособие составлено в соответствии с методическими указаниями по высшей математике, разработанными учебнометодическим управлением по высшему образованию, и с учетом особенностей учебных программ, по которым обучаются студенты в Кузбасском государственном техническом университете. Пособие содержит программу, методические указания и контрольные задания по теории вероятностей и математической статистике (контрольные работы №7 и 8). Назначение его – дать индивидуальные контрольные задания и помочь студентам в решении практических задач.
При его составлении участвовали преподаватели кафедры Л.Е. Мякишева, Т.К.Скадина, Э.Ф.Золотарева, О.А. Зубанова, Е.А. Волкова, Е.В.Прейс, О.С.Георгинская, И.А.Ермакова.
Выбор варианта индивидуального задания по теории вероятностей (контрольная работа № 7) осуществляется по табл.1: номера задач варианта находятся на пересечении строки, определяемой по первой
букве фамилии студента, и столбца, определяемого по последней циф- |
|
ре шифра. |
|
Номер варианта индивидуального задания студента по статистике |
|
(контрольная работа № 8) определяется как |
целая часть (Е) числа |
к = 0,4 (m+n), где m – последняя цифра шифра, |
n – номер первой бук- |
вы фамилии в алфавите |
|
А |
Б |
В |
Г |
|
Д |
|
Е |
|
Е |
|
Ж |
З |
|
И |
|
К |
|
Л |
|
М |
Н |
О |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
П |
Р |
С |
Т |
У |
Ф |
Х |
Ц |
Ч |
Ш |
Щ |
Ы |
|
Э |
Ю |
Я |
|||||||
16 |
17 |
18 |
19 |
|
20 |
|
21 |
|
22 |
|
23 |
24 |
25 |
|
26 |
|
27 |
28 |
29 |
30 |
||
Например, Юрин Ю.П. (шифр ЭУз – 98276) выполняет в контрольной работе № 7 номера: 6, 21, 41, 49, 61 (пересечение 6 строки и 6 столбца таблицы № 1) и вариант 14 (к = Е[0,4 (6 + 29)] = E(14,0) = 14 ) контрольной работы № 8.
2
Таблица 1
Первая |
|
|
|
Последняя цифра шифра |
|
|
|
||||
буква |
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
0 |
||
фамилии |
|||||||||||
А З |
1 27 |
14 25 |
5 22 |
14 21 |
5 28 |
11 21 |
1 30 |
5 23 |
8 19 |
10 16 |
|
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
||
И Ц |
49 70 |
57 69 |
50 68 |
58 67 |
51 66 |
59 65 |
52 64 |
60 63 |
53 62 |
46 61 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 26 |
2 23 |
15 20 |
6 29 |
15 22 |
6 16 |
12 24 |
2 17 |
6 17 |
9 25 |
|
Ч Б |
41 |
42 |
43 |
44 |
45 |
31 |
32 |
33 |
33 |
35 |
|
П Р |
50 75 |
58 74 |
51 73 |
59 72 |
52 71 |
60 70 |
53 69 |
46 68 |
54 67 |
47 66 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Э С |
14 24 |
9 19 |
3 30 |
1 24 |
7 17 |
1 25 |
7 18 |
13 18 |
3 24 |
7 26 |
|
36 |
37 |
36 |
39 |
40 |
41 |
42 |
43 |
44 |
45 |
||
В К |
51 65 |
59 64 |
52 69 |
60 62 |
53 61 |
46 75 |
54 74 |
47 73 |
55 72 |
48 71 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 18 |
15 16 |
10 24 |
14 18 |
12 26 |
8 16 |
2 19 |
8 23 |
14 27 |
4 19 |
|
Л Т |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
|
Ш Г |
52 61 |
60 62 |
53 63 |
46 64 |
54 65 |
47 66 |
55 67 |
48 68 |
56 69 |
49 70 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 17 |
5 25 |
1 19 |
2 27 |
5 30 |
3 20 |
9 22 |
3 28 |
9 18 |
15 20 |
|
Д М |
41 |
42 |
43 |
44 |
45 |
31 |
32 |
33 |
34 |
35 |
|
У Щ |
53 75 |
46 74 |
54 73 |
47 72 |
55 71 |
48 70 |
56 69 |
49 68 |
57 67 |
50 66 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Ю Е |
2 26 |
9 20 |
6 28 |
2 29 |
12 21 |
6 21 |
4 29 |
10 17 |
4 21 |
10 24 |
|
36 |
37 |
38 |
39 |
40 |
41 |
42 |
45 |
44 |
45 |
||
Н Ф |
54 71 |
47 72 |
55 73 |
48 74 |
56 75 |
49 61 |
57 62 |
50 65 |
58 64 |
51 65 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 27 |
12 29 |
10 28 |
7 22 |
13 20 |
13 30 |
7 16 |
11 22 |
12 23 |
13 25 |
|
Х Ж |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
|
О Я |
55 70 |
48 69 |
56 68 |
49 67 |
57 66 |
50 65 |
58 64 |
51 63 |
59 62 |
52 16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3
Программа
1.Теория вероятностей
1.Основные понятия теории вероятностей: испытание, событие, вероятность.
2.Статистическое, классическое и геометрическое определение вероятности.
3.Алгебра событий (сложение и умножение событий). Противоположные события.
4.Теоремы сложения и умножения вероятностей и следствия из них.
5.Теорема о полной вероятности события. Формула Байеса.
6.Повторные независимые испытания. Формулы Бернулли, Пуассона, Муавра-Лапласа.
7.Понятие случайной величины, их типы. Законы распределения вероятностей дискретной случайной величины (табличный, графический).
8.Функция распределения вероятностей случайной величины, ее свойства. Плотность вероятностей случайной величины, ее свойства.
9.Числовые характеристики случайной величины: математическое ожидание, дисперсия, среднее квадратическое отклонение.
10.Основные законы распределения случайных величин: нормальный, равномерный, показательный, биномиальный.
11.Закон больших чисел. Теоремы Бернулли и Чебышева. Центральная предельная теорема Ляпунова.
2.Математическая статистика
1.Генеральная совокупность и выборка. Вариационный ряд. Гистограмма и полигон частот. Эмпирическая функция распределения.
2.Числовые характеристики вариационного ряда: выборочное среднее, выборочная дисперсия и среднее квадратическое отклонение.
3.Доверительная вероятность, доверительные интервалы для выборочного среднего и среднего квадратического отклонения.
4.Понятие о критериях согласия. Проверка гипотез о теоретическом законе распределения, о равенстве средних и дисперсий генеральных совокупностей.
5.Элементы теории линейной регрессии и корреляции.
6.Понятие о нелинейной и множественной регрессии. Корреляционное отношение, коэффициенты парной корреляции.
4
Методические указания к контрольной работе по теории вероятностей
При определении вероятности события в задачах 1-15 по классической формуле P( A ) = mn ([1] гл. 1; [2] гл. 1) расчет числа исходов ис-
пытания (m и n) часто осуществляется с помощью элементов комбинаторики: перестановок, размещений и сочетаний.
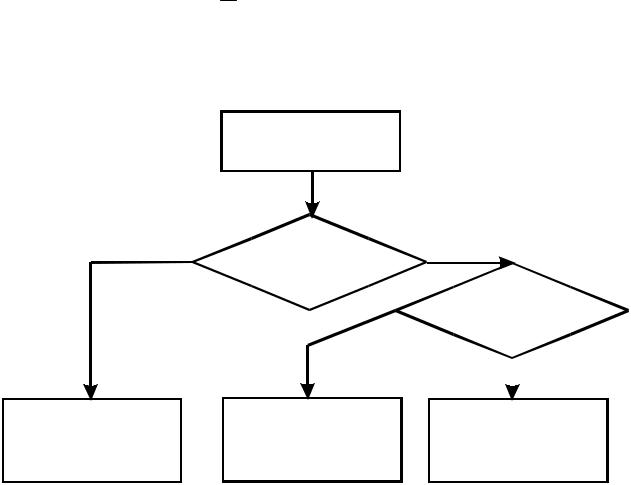
Выбор вида соединения удобно проводить по блок-схеме:
Соединения из n элементов по k
да |
Все ли элементы |
|
входят |
|
а |
|
д |
Перестановки Размещения
Pn = n!= n (n− 1)...3 2 1 |
Ak |
= |
n ! |
|
(n − k)! |
||||
n |
|
|||
|
|
|
нет
Важен ли порядок элементов?
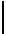 нет Сочетания
нет Сочетания
Cnk = |
n! |
|
|
k!(n − k)! |
|||
|
|||
Пример 1. Имеется пятитомное собрание сочинений. Сколькими способами можно:
1)расставить книги на полке;
2)выбрать из них любые три тома;
3)выбрать и расставить на полке три тома?
Решение. В первом случае имеем дело с упорядоченным множеством из 5 элементов, т.е. в соединение входят все элементы. При этом на первое место можно поставить любой из пяти элементов (книг), на второе – любой из оставшихся четырех элементов, на третье – из трех, на четвертое – из двух, на пятое остается один элемент. Таким образом, число способов расстановки книг на полке равно 5·4·3·2·1 = 5! = 120 - числу перестановок из всех пяти имеющихся элементов (P5 = 5!).
5
Во втором случае, выбирая три книги из пяти, мы имеем дело с соединениями, отличающимися друг от друга хотя бы одним элементом (порядок не важен) - это сочетания из пяти элементов по три. Их число равно
C53 = |
5! |
|
= |
5 4 3! |
= 10. |
||
|
|
|
|
||||
3! 2! |
3! 2! |
||||||
|
|
|
|||||
А в последнем случае при расстановке трех книг на полке внутри каждой тройки книг учитываем все возможные перестановки из трех элементов (Р3) и общее число соединений, отличающихся либо элементом, либо их порядком, – это есть размещения из пяти элементов по
три, т.е. |
|
5! |
|
|
|
A3 = |
|
|
= 3 4 5 = 60 . |
||
(5 |
− 3) ! |
||||
5 |
|
||||
|
|
|
|
||
Пример 2. Найти вероятности того, что номера трех томов, выбранных поочередно из данных пяти, будут идти в возрастающем порядке.
Решение. Обозначим через A интересующее нас событие. Число (n) всех возможных нумераций трех книг из пяти определяется по фор-
муле для числа размещений n = A53 = 60 . Число же тех нумераций, которые дают только возрастание томов без учета перестановок внутри
каждой тройки, определяется |
|
по |
|
формуле для числа сочетаний |
||||||
m = C53 = 10 . Отсюда P( A) = |
m |
|
= |
10 |
= |
|
1 |
. |
||
n |
|
|
60 |
|
6 |
|||||
|
|
|
|
|||||||
При нахождении вероятностей сложных событий в задачах 16-30 следует пользоваться теоремами сложения, умножения и следствиями из них ([1] гл.2-4; [2] гл. 2).
Пример 3. Два стрелка делают по одному выстрелу. Вероятность поражения мишени первым стрелком равна 0,8, а вторым – 0,7. Найти вероятности попадания в мишень обоими стрелками; поражения мишени хотя бы одним стрелком.
Решение. Пусть событие A – попадание в мишень первым стрелком, B – вторым. Тогда событие C, заключающееся в одновременном поражении мишени обоими стрелками, является произведением событий А и В (С = А·В). Эти события происходят независимо друг от друга. Поэтому вероятность их произведения определяется по формуле
P(А·В) = Р(А) Р(В) и равна P(С) =Р(А·В) = 0,7·0,8 = 0,56.
6
Рассмотрим теперь событие D – поражение цели хотя бы одним стрелком. Оно заключается в поражении мишени либо первым стрелком, либо вторым, либо обоими вместе. Это событие является суммой исходных событий, т.е. D = А + В. События А и В являются совместными, т.к. могут происходить в одном и том же испытании. Поэтому следует воспользоваться формулой Р(А+В) = Р(А) + Р(В) – –Р(А·В).
Получим Р(D) = Р(А+В) = 0,7 + 0,8 - 0,7 0,8 = 0,94.
Пример 4. Пластмассовые заготовки для деталей поступают с пресса №1, выпускающего 50% всей продукции, с пресса №2, выпускающего 30%, и с пресса №3, дающего 20%. При этом доля нестандартной продукции у первого пресса 0,10, у второго – 0,05, а у третьего
– 0,02. Наудачу взятая заготовка оказалась стандартной. Определить вероятность того, что она поступила с первого пресса.
Решение. Событие А – взятая заготовка стандартная. Она могла быть изготовлена прессом №1 (гипотеза Н1), прессом №2 (гипотеза Н2) или прессом №3 – Н3. Вероятности этих гипотез соответственно равны Р(Н1)=0,5; Р(Н2)=0,3; Р(Н3)=0,2. Событие А может произойти с событием Н1 с условной вероятностью PH1 (A) = 1- 0,1 = 0,9 . Аналогично имеем
условные вероятности: |
|
|
PH2 (A) = |
1 − 0,05 = 0,95; |
PH3( A) = 1 − 0,02 = 0,98. |
Тогда полная |
вероятность события А, определяемая по формуле |
|
P( A) = ∑3 P(H j ) PHj ( A),
j = 1
равна P(A) = 0,5 0,9 + 0,3 0,95 + 0,2 0,98 = 0,931.
Для нахождения вероятности РА(Н2) – того, что заготовка изготовлена первым прессом, при условии, что она стандартная, применим
формулу Байеса: |
|
P(H j ) PH j (A) |
|
|||||
|
|
|
|
PA (H j ) = |
, |
|||
|
|
|
|
|
|
|||
|
|
|
P(A) |
|||||
|
|
|
|
0,5 0,9 |
|
|
||
получаем P |
(H |
1 |
) = |
≈ 0,483. |
|
|||
|
|
|||||||
A |
|
0,931 |
|
|
|
|
||
|
|
|
|
|
|
|
||
Аналогично можно найти условные вероятности гипотез Н1 и Н3. |
||||||||
При этом должно выполняться условие PA (H1 ) + |
PA (H 2 ) + PA (H3 ) = 1. |
|||||||

7
Для решения задач №30-45 следует знать условия, к которым применимы формулы Бернулли, Пуассона, локальная и интегральная теоремы Муавра-Лапласа ([1], гл. 5, 6 §5; [2], гл. 3, 4 §1).
Пример 5. Монету подбрасывают 5 раз. Найти вероятность того, что герб выпадет ровно 2 раза.
Число повторных независимых испытаний – подбрасываний монеты n = 5 – мало. Вероятность выпадения герба в одном испыта-
нии p = 12 , вероятность противоположного события – выпадения циф-
ры: q = 1 − |
p = |
1 |
. Тогда вероятность выпадения двух гербов (к = 2) сле- |
||||||||||||||||||||
2 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
P |
(к) = |
C к pк qn − к |
: |
|
|
|
|||||||
дует определять по формуле Бернулли |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
1 2 |
|
1 3 |
n |
|
|
|
n |
|
|
|
|
|
|
||||
|
|
|
|
C 2 |
|
|
|
5! |
|
|
1 |
|
|
4 5 |
|
5 |
|
||||||
|
|
P (2) = |
|
|
|
|
|
|
= |
|
|
|
|
|
= |
|
= |
|
|
. |
|||
|
|
|
|
3! 2! |
32 |
|
2 32 |
16 |
|||||||||||||||
|
|
5 |
5 |
|
2 |
|
2 |
|
|
|
|
|
|
||||||||||
Пример 6. В городе каждая десятая машина – иномарка. За час по центральной улице проезжает 900 машин. Какова вероятность того, что иномарки составляют среди них не более 90 машин.
Решение. Число независимых испытаний n = 900 – велико, а веро-
ятность появления иномарки p = 101 не близка к нулю. В этих условиях
используют приближенные формулы Муавра – Лапласа. Так как нас интересует вероятность появления события не более 90 раз, то приме-
ним интегральную формулу P(к1, к2 ) ≈ |
|
Ф(х2 ) − |
Ф(х1) , получим |
||||||||||||||||||
P900 ( не более 90) = |
|
P900 (0,90) = |
P900 (0 ≤ |
|
|
|
k ≤ |
90) ≈ |
Ф(х2 ) − Ф(х1), где |
||||||||||||
x = к1 − np = |
0 − |
900 |
|
1 |
|
|
|
|
|
|
|
|
− |
90 = |
|
||||||
10 |
|
|
|
|
= |
|
− 30, |
||||||||||||||
1 |
|
npq |
100 |
1 |
|
|
9 |
|
|
|
|
|
|
3 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
10 |
|
10 |
|
|
1 |
|
|
|
|
|
|||||||
|
|
к2 − np |
|
90 − 900 |
|
|
0 |
|
|
||||||||||||
x2 |
= |
= |
10 |
|
= |
= |
0. |
||||||||||||||
npq |
100 |
|
1 |
|
|
|
|
9 |
|
3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
10 |
|
10 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
По прил. 1 определим значения функции Лапласа Ф(0) = 0, Ф(–30) = –Ф(30) = – 0,5 (функция Лапласа нечетная Ф(–х) = – Ф(х) и при x > 5
Ф(х) = 0,5).

8
Итак, Р900(не более 90) = 0 + 0,5 = 0,5.
Пример 7. Учебник издан тиражом 10000 экземпляров. Вероятность его неправильной брошюровки равна 0,0001. Найти вероятность того, что тираж содержит две бракованные книги.
Решение. Так как число испытаний n = 10000 – велико, а вероятность p = 0,0001 близка к нулю, то используем формулу Пуассона. Для
этого определим параметр λ |
= np = 1 и вычислим |
||||||
P |
(2) = |
λ кe− λ |
= |
12 e− 1 |
= |
1 |
≈ 0,18. |
|
|
|
|||||
10000 |
|
к! |
2! |
|
2e |
||
|
|
|
|||||
Закон распределения дискретных случайных величин, их числовые характеристики (задачи №46-60) рассмотрены в гл. 6-8 [1], гл.4 [2],
гл.11 [3].
При составлении закона распределения случайной величины для нахождения вероятностей возможных значений можно использовать основные теоремы и формулы теории вероятностей.
Пример 8. Рабочий обслуживает два станка. В течение смены первый станок потребует внимания рабочего с вероятностью 0,2, второй – с вероятностью 0,3. Составить закон распределения числа станков, потребовавших внимания рабочего в течение смены. Вычислить его числовые характеристики.
Решение. Дискретная случайная величина Х – число станков, потребовавших внимания рабочего. Обозначим событие Аi – внимание потребовал i-й станок, тогда, Ai – i-й станок не потребовал внимания
рабочего. Итак, Р(А1) = 0,2, P( A1) = 1 – Р(А1) = 0,8, Р(А2) = 0,3, P(A2 ) = =1 – Р(А2) = 0,7.
Определим вероятность того, что случайная величина Х примет возможные значения 0, 1, 2:
P( X = 0) = P( |
|
1 |
|
|
|
|
2 ) = P( |
|
1) P( |
|
1) = |
0,8 0,7 = |
0,56; |
|
|||||||||||||
A |
A |
A |
A |
||||||||||||||||||||||||
P( X = 1) = P( A1 |
|
|
|
2 + |
|
1 A2 ) = P( A1 |
|
2 ) + P( |
|
1 |
|
2 ) = |
|||||||||||||||
A |
A |
A |
A |
A |
|||||||||||||||||||||||
= P( A1)P( |
|
2 ) + P( |
|
1)P( A2 ) = |
0,2 0,7 + |
0,8 0,3 = |
0,14 + 0,24 = 0,38; |
||||||||||||||||||||
A |
A |
||||||||||||||||||||||||||
P( X = 2) = P( A1) P( A2 ) = 0,2 0,3 = 0,06. |
|
|
|
|
|||||||||||||||||||||||
Составим закон распределения: |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
Х |
|
0 |
|
|
1 |
|
2 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
Р |
|
|
|
|
0,56 |
|
|
0,38 |
|
|
0,06 |
|
|
|
||||||||||

9
Контроль: ∑3 |
pi = |
0,56 + 0,38 + |
|
0,06 = 1. |
|
|
|
|||
|
|
i = 1 |
|
|
|
|
|
|
|
|
Вычислим основные числовые характеристики: |
||||||||||
математическое ожидание М(Х), |
|
|
|
|
||||||
М (Х ) = |
∑3 |
xi |
pi = |
0 0,56 + 1 0,38 + 2 0,06 = |
0,5, |
|
||||
|
i= 1 |
|
|
|
|
|
|
|
|
|
дисперсию D(Х) = М(Х2) - (М(Х))2. Для этого составим закон распреде- |
||||||||||
ления квадрата случайной величины Х: |
|
|
||||||||
|
|
Х2 |
|
0 |
|
1 |
|
4 |
|
|
М(Х2) = |
|
Р |
|
0,56 |
|
0,38 |
|
0,06 |
|
|
0·0,56 + 1·0,38 + 4·0,06 = 0,62, |
|
|
|
|||||||
D(Х) = 0,62-(0,5)2 = 0,37. |
|
|
|
|
||||||
Среднее квадратическое отклонение: |
|
|
||||||||
σ ( X ) = |
D(Х ) = |
|
0,37 ≈ 0,61. |
|
|
|
|
|||
В ряде задач на повторные независимые испытания вычисление вероятностей возможных значений случайной величины и ее числовых характеристик упрощается.
Пример 9. Каждый из трех независимо работающих приборов регистрирует уровень шума, превышающий установленную норму с вероятностью 0,9. Составить закон распределения числа приборов, зарегистрировавших шум, превышающий норму. Вычислить его числовые характеристики.
Решение. Случайная величина Х – число приборов, зарегистрировавших превышение уровня шума, может принимать четыре значения (к = 0, 1, 2, 3); соответствующие вероятности найдем по формуле Бер-
нулли при n = 3; p = 0,9; q = 1– p = 0,1; к = 0, 1, 2, 3.
P(X = 0) = P3(0) = C30p0q3 = 0,001, P(X = 1) = P3(1) = C31p1q2 = 0,027, P(X = 2) = P3(2) = C32p2q1 = 0,243, P(X = 3) = P3(3) = C33p3q0 = 0,729.
Запишем закон распределения случайной величины:
|
0 |
|
|
1 |
|
2 |
|
3 |
|
0,001 |
|
|
0,027 |
|
0,243 |
|
0,729 |
Контроль: ∑3 |
pi = |
0,01+ 0,027 + |
0,243 + 0,729 = |
1. |
||||
|
i = 1 |
|
|
|
|
|
|
|
