Добавил:

fench Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Кузбасский государственный технический университет

Предмет:

Высшая математика

Файл:

Е.Н. Грибанов Высшая математика. Контрольные работы №4, 5, 6 и методические указания к ним для студентов-заочников инженерно-технических специальностей

.pdf

Скачиваний:

Добавлен:

19.08.2013

Размер:

382.82 Кб

Скачать

☆

1 / 51 2 3 4 5 > Следующая >>>

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

КУЗБАССКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра прикладной математики

ВЫСШАЯ МАТЕМАТИКА

Контрольные работы № 4, 5, 6 и методические указания к ним для студентов-заочников инженерно-технических специальностей

Составители: Е.Н. Грибанов В.А. Похилько З.П. Бадяева Э.Ф. Золотарёва В.И. Немов

Утверждены на заседании кафедры Протокол № 2 от 29.02.00 Рекомендованы к печати учебнометодической комиссией специальности 060400 Протокол № 5 от 10.03.2000 Электронная копия находится в библиотеке главного корпуса КузГТУ

Кемерово 2001

- 1 -

ВВЕДЕНИЕ

Данные контрольные работы составлены в соответствии с методическими указаниями по высшей математике, разработанными учебнометодическим управлением по высшему образованию, с учетом особенностей учебных программ специальностей, по которым обучаются в Кузбасском государственном техническом университете. Контрольные работы № 4, 5, 6 выполняют во втором семестре. Номера задач контрольной работы определяют по таблице. В первом столбце студент находит первую букву своей фамилии, в первой строке таблицы - последнюю цифру номера зачётной книжки и берёт номера, находящиеся на пересечении строки (с первой буквой фамилии) и столбца (с последней цифрой шифра). Например, студент А. И. Петров, имеет номер зачётной книжки 98438. Буква «П» находится в шестой строке, последняя цифра «8» попадает в девятый столбец, на их пересечении записаны номера 29; 39; 78; 106; 136. Студент А.И. Петров в каждой контрольной работе выполняет задания под данными номерами.

ПРОГРАММА КУРСА

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

1. Понятие производной. Физический и геометрический смысл производной.

2.Производная суммы функций, произведения и частного.

3.Производная сложной функции, производная обратной функ-

ции.

4.Производные основных элементарных функций.

5.Нахождение производной от неявной функции и с помощью предварительного логарифмирования.

6.Производные высших порядков.

7.Дифференциал функции и его применение.

8.Производная от параметрически заданной функции. ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНЫХ

9.Условия возрастания и убывания функции. Точки экстремума. Необходимое условия экстремума. Достаточные признаки существования экстремума. Отыскание наибольшего и наименьшего значения функций непрерывных на замкнутом промежутке или на открытом интервале.

- 2 -

10. Исследование функции на экстремум с помощью производной второго порядка. Исследование функции на выпуклость и вогнутость. Точки перегиба. Асимптоты кривых. Общая схема построения графика функции.

ВЕКТОРНАЯ ФУНКЦИЯ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО 11. Векторная функция скалярного аргумента. Первая и вторая

производная, их механический смысл.

12. Параметрические уравнения кривой на плоскости и в пространстве.

ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ 13. Функции нескольких переменных. Область определения. Пре-

дел функции, непрерывность.

14. Частные производные. Полный дифференциал и его геометрический смысл.

15. Касательная плоскость и нормаль к поверхности.

16. Частные производные и полные дифференциалы высших порядков.

17. Экстремум функции нескольких переменных. Необходимые условия. Достаточные условия.

18. Наибольшее и наименьшие значения функции двух переменных в замкнутой области. Условный экстремум.

- 3 -

Выбор номеров задач контрольных работ

Началь-			Последняя цифра шифра зачётной книжки
ная бук-			Последняя цифра шифра зачётной книжки
ная бук-
ва фами-	0	1	2	3	4	5	6	7	8	9
лии	0	1	2	3	4	5	6	7	8	9
лии

	1, 31, 80,	2, 32, 79,	3, 33,78,	4, 34, 76,	5, 35, 76,	6, 36, 75,	7, 37, 74,	8, 38, 73,	9, 39, 72,	10,40,71,
А, В, Д	110, 130.	100, 150.	101, 131.	120, 130.	91, 141.	110, 140.	111, 121.	100, 150.	101, 131.	120, 130.

	11,41,70,	12,42,69,	13,43,68,	14,44,67,	15,45,66,	16,46,65,	17,47,64,	18,48,63,	19,49,62,	20,50,61,
Б, Е, З	109, 129.	99, 149.	102, 132.	119,129.	92, 142.	109, 139.	112, 122.	99, 149.	102, 132.	119, 129.
	21,51,80,	22,52,79,	23,53,78,	24,54,77,	25,55,76,	26,56,75,	27,57,74,	28,58,73,	29,59,72,	30,60,71,
Г, Ж, И, Л	108, 128.	98, 148.	103, 133.	118, 128.	93, 143.	108, 138.	113, 123.	98, 148.	103, 133.	118, 128.
	1, 60, 90,	2, 59, 89,	3, 58, 88,	4, 57, 87,	5, 56, 89,	6, 55, 85,	7, 54, 84,	8, 53, 83,	9, 52, 82,	10,51,81,
К	107, 127.	97, 147.	104, 134.	117, 127.	94, 144.	107, 137.	114, 124.	97, 147.	104, 144.	117, 127.
	11,49,70,	12,48,61,	13,47,62,	14,46,63,	15,45,64,	16,44,65,	17,43,66,	18,42,67,	19,41,68,	20,42,69,
М, Н, О	196, 126.	96, 148.	105, 135.	116, 126.	95, 145.	106, 136.	115, 125.	96, 146.	105, 135.	116, 126.
	21,31,80,	22,32,71,	23,33,72,	24,34,73,	25,35,74,	26,36,75,	27,37,76,	28,38,77,	29,39,78,	30,40,79,
П, Ы	105, 125.	95, 145.	106, 136.	115, 125.	96, 146.	105, 135.	116, 126.	95, 145.	106, 136.	115, 125.
	1, 60, 90,	2, 59, 81,	3, 58, 82,	4, 57, 83,	5, 56, 84,	6, 55, 85,	7, 54, 86,	8, 53, 87,	9, 52, 88,	10,51,89,
С, У	104, 134.	94, 144.	107, 137.	114, 124.	97, 147.	104, 134.	117, 127.	94, 144.	107, 137.	114, 124.
	11,50,70,	12,49,61,	13,48,62,	14,47,63,	15,46,64,	16,45,65,	17,44,66,	18,43,67,	19,42,68,	20,41,69,
Р, Т, Ф	103, 123.	93, 143.	108, 138.	113, 123.	98, 148.	103, 133.	118, 128.	93, 143.	108, 138.	113, 123.
	21,40,80,	22,39,71,	23,38,72,	24,37,73,	25,36,74,	26,35,75,	27,34,76,	28,33,77,	29,32,78,	30,31,79,
Ц, Х, Ш	102, 122.	92, 142.	109, 139.	112, 122.	99, 149.	102, 132.	119, 129.	92, 142.	108, 139.	112, 122.
Ч, Щ, Э,	1, 51, 90,	2, 52, 81,	3, 53, 82,	4, 54, 83,	5, 55, 84,	6, 56, 85,	7, 57, 86,	8, 58, 87,	9, 59, 88,	10,60,89,
Ю, Я	101, 121.	91, 141.	110, 140.	11, 121.	100, 150.	101, 131.	120, 130.	91, 141.	110, 140.	111, 121.

- 4 -

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ

Контрольная работа № 4 В данную контрольную работу включены задачи дифференциаль-

ного исчисления функции одной переменной. По каждой изучаемой теме приведены ссылки с указанием страниц. Ссылки даны на несколько учебников, пользоваться можно любым из них.

Для решения задач № 1-30 необходимо проработать литературу: [1, гл. VI, § I, п. 8, 14; 2 гл. III, § 1-15, § 20; 4, гл. VI, § 1, 3], выписать и выучить таблицу производных основных элементарных функций и правила дифференцирования. Особое внимание следует обратить на правило дифференцирования сложной функции [1, гл. VI, § 1, п. 11, с 221-223; 3, с 63; 4, с 221]. Очень важно научиться правильно представлять слож-

ную функцию цепочкой элементарных функций. Например, y = tg2 2x - это сложная функция. Представим её в виде цепочки элементарных

функций. Рассуждаем так: задана степенная функция y = u2 . Сложной она считается потому, что её аргумент u сам является функцией (тригонометрическойu = tgv ) и опять сложной, т. к. её аргумент v есть линей-

ная функция v =

2x . Итак,

мы получили цепочку элементарных функ-

ций: y =

u2 , u =

tgv , v =

2x. Найдём производную данной функции. По

правилу дифференцирования сложной функции,

′

′ ′

имеем yx =

yuux , где

′

= (u

2 ′

′

v ( 2x)

′

x =

2x .

= uv vx

= yu uv

vx , т. е.

)u (tgv)

cos2 v

x ,

Подставляя

вместо

их

выражения

через

получаем

y′x

= 2tg2x

2 = 4

tg2x

cos2

cos2 2 x

Рассмотрим другой пример. Функцию y = e(2 x 2 +

3) можно представить

как y = eu, где u = 2x2 + 3, тогда

y′x = (eu)′x =

(eu)′u u′x =

eu(

2x2 +

′x =

e2 x2 + 3 4x . Функцию

y =

ln(sin3x)

можно представить цепочкой y =

ln u , где u =

sinv ,

v =

3x . Тогда:

3cos3x

′

′ ′

= (lnu) u( sinv)

v( 3x)

cosv =

= 3ctg3x .

= yuuvvx

sin3x

- 5 -

Если заданы сумма, произведение или частное функций, то нужно обратится к правилам дифференцирования [3, § 7 с. 77-79; [5], гл.VI, § 1, с. 217-219]. Например, для определения производной функции

y =

ctg4 x + ln 2x −

x2 следует применить правила: (u ± v)′x =

u′x ± v′x

и (c u)′x =

c u′x . Тогда:

′

((ctgx) 4 )x′ +

y′x

ctg

4 x

′ +

(ln 2x) x′ − (x

2 ) x

(2x)′

−

2x =

ctg3 x

4 ctg

3 x

−

− 2 x =

−

− 2x.

2 x

3 sin2 x

sin2 x

Для определения производной функции y =

sin3 x cos(x2 ) применим

правило дифференцирования произведения двух функций:

(u v)′x =

u′x

v +

u v′x . Тогда:

y′x =

(sin3 x)′ cos(x2 )+

sin3 x (cos(x2 ))′

= 3sin2 x (sin x)′ cos(x2 )+

sin3 x (−

sin(x2))( x2)

′

= 3 sin2 x cos x cos(

x2)

sin3 x(−

sin( x)2 )2x =

3 sin2 x cos x cos(x2 )−

2 x sin3 x sin(x2 ).

−

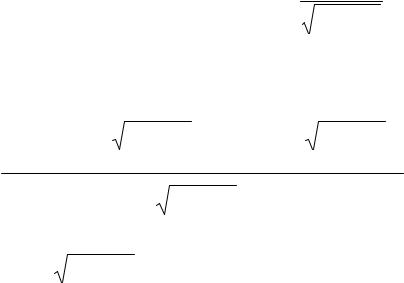
Для определения производной функции y =

применим прави-

e2 x

u ′

u′ v −

u v′

ло дифференцирования частного двух функций:

′

− 1

e2 x +

3 −

−

e2 x

+ 3

Тогда: y′

2 x

+ 3

− 1 ′

e2 x

+ 3 − ln

− 1

(e2 x + 3)−

(e2 x + 3)′

− 1

e2 x + 3

- 6 -

e2 x +

3 − ln

− 1

2e2 x

−

2 e2 x + 3

e2 x + 3

При решении задач № 1-30 (пункт г) изучите литературу [1, гл. VI,

§3, п.1, с. 232-234; 2, § 12, c. 88].

Пример: Найти дифференциал функции y = (x2 + 7)arcsin x . Ис-

пользуем формулу: dy =

y′xdx . При определении y′x нельзя воспользо-

ваться ни производной степенной функции (xn )′, ни производной пока-

зательной функции (a x )′, так как здесь и основание, и показатель степени - переменные величины. Поэтому предварительно прологарифмиру-

ем данную функцию и используем свойство

lnab = b lna . Получаем

ln y = ln(x2 +

7)arcsin x =

arcsin x ln(x2 + 7). Продифференцируем это ра-

венство по x , тогда: (ln y)′ y =

(arcsin x ln(x2 +

7))′x или

y′x =

(arcsin x)′x ln(x2 +

7)+

arcsin x(ln(x2 +

7))′x отсюда следует:

ln(x 2 +

7)+

y′x

arcsin x

2 x

или

x 2 +

1 − x 2

ln(x2 + 7)

2x arcsin x

y′x

= y

1−

= (x2 +

arcsin x

7) + 2 x arcsin x

ln(x

1−

Окончательно получаем

dy = (x2 +

arcsin x

ln(x

+ 2 x arcsin x dx .

1−

+ 7

задачах № 1-30 (пункт д) функция задана неявно уравнением

F (x; y)

= 0. Для нахождения производной следует дифференцировать

все члены уравнения по

x , не забывая,

что

y есть функция от x , [1,

гл. VI, § 1, п. 15, с. 225-227; 2, § 11, с. 85; 3, с. 75].

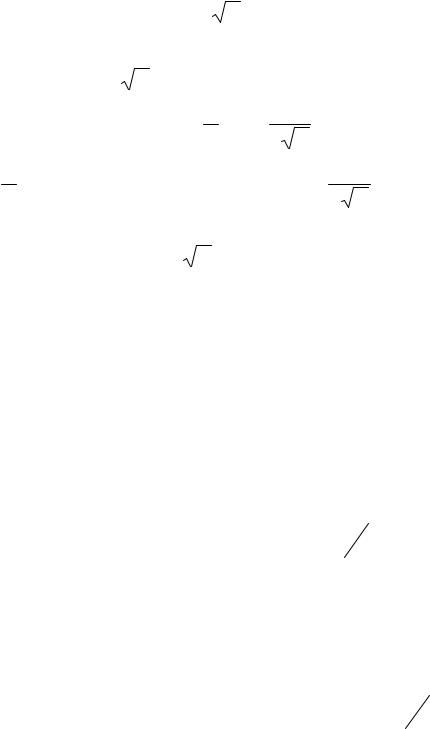
- 7 -

Пример. Найти производную y′x от неявной функции, заданной

выражением: cos5x2 ln y +

x +

y3 =

Решение. Продифференцируем заданное выражение получим:

(cos5x2 ln y)′x + (

x)′x +

(y3 )′x =

0 или

− sin5x

10x ln y

cos5x

y′x

3 y

y′x

0 отсюда

2 x

cos5x

+ 3 y

ln y

0 или

y′x

− 10x sin5x

10x sin5x2 ln y −

y′x =

cos5x2

3 y2

При решении задач № 31-60 (пункт а) рекомендуется использовать

литературу [1, гл. VI, § 1, п. 1, п.11, п. 14, § 2, п. 1, § 4, п. 2; 5, гл. VI,

§ 2]. Для того, чтобы найти значения производных

d 2 y

в задан-

ной точке

x0 , найдём сначала производные,

а затем подставим задан-

ные значения.

d 2 y

Пример. Найти

при x0 =

и y = ln sin3x .

dx2

Решение. Найдём

(ln sin3x)

′ =

cos3x 3 =

3ctg3x и

d 2 y

sin3x

(3ctg3x)′

−

3 =

−

dx2

sin2

sin2 3x

Теперь найдём значения производных при x

. Получаем

3 ctg

3ctg

0 и

											- 8 -
d 2 y						= −		9		= −	9			= − 9 .
d 2 y								9			9
dx	2			π			sin2		π		sin	2 π
		x0	=					3
													2
									6
					6				6

Для решения задач № 31-60 (пункт б) изучите дифференцирование функций заданных параметрически [1, гл. VI, § 4, п. 2; 3, гл. II, § 10; 4,

гл. VI, § 4].

Пример. Найти первую и вторую производные функции, заданной

параметрически

, и вычислить их значения при t0

arcsint

Решение. Найдём

′

= (arcsint

′

;

1− (t 2 )2

1− t 4

′

ln5 2. Тогда:

yt′

1− t 4

. Следо-

xt =

xt′

2 52t ln5

1− t 4

52t

ln5

вательно

0,5

≈

0,06. Для нахождения

d 2 y

1− 0

,54 52 0,5 ln5

′′

′

′′

используем формулу

ytt

xt −

xtt

. Найдём

′

(xt )

′

t 1−

−

1−

′′

′

(2t)

t =

ytt =

( yt )

1− t 4

1−

2 1− t 4 − 2t

− 4t3

2(1− t 4) + 4t

2(1+ t 4)

2 1− t

;

1− t 4

(1− t 4 )32

′′

′

2t ′

2 2t

(2ln5 5

) t

= 2 ln5(5 ) t = 2 ln5 5 2 ln5 = (2ln5) 5 .

xtt =

(xt ) t =

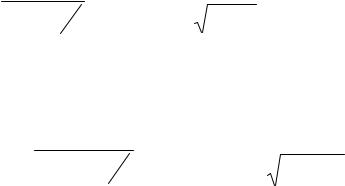
Тогда

- 9 -

2(1+

t 4 )

52t 2ln5 −

(2ln5)2 52t

(1− t 4)3

d 2 y

1− t 4

dx2

(2 ln5 52t )3

Подставив заданное значение, получим

2(1+ 0,54 )

52 0,5

2 ln5 −

0,5

(2ln5) 2 52 0

− 0,54)32

d 2 y

1− 0,54

≈ − 0,004.

dx2

(2ln5 52 0,5)3

t =

Для решения задач № 61-90 необходимо изучить литературу: [1,

гл. VI, § 5, п. 2-4; 4, гл. VI, § 5].

Пример. Дано уравнение движения точки

e3t

+ (t 2 −

определим скорость и ускорение

r (t) =

sint ) j +

2arctgt k ,

точки в момент t0 = 0 .

Решение. Траектория точки есть годограф её радиуса-вектора r (t) ,

sin t ;2arctgt}, т. е. линия определяемая параметрическими

r = {e3t ;t 2 −

x =

y =

t 2 − sin t

(1)

уравнениями

2arctgt

z =

исходя из ме-

Скорость v и ускорение w движения точки определяем,

ханического смысла первой и второй производных векторной функции

скалярного

аргумента

[4,

гл.

VI,

с.

224;

с.

202]. Тогда

! !

′

3t ′ !

′

v = r

)

i + (t

−

sin t)

j +

(2arctgt)

k =

(t)

e3t

(2t −

cos t)

3 i

k ;

t 2

′′

3t ″

″

w = r

)

i +

−

sint )

j +

(2arctgt)

k =

(t) =

′

(3e

)

(2t −

cos t)

′

j +

k =

i +

(2 +

sint) j +

t 2

1 / 51 2 3 4 5 > Следующая >>>

Соседние файлы в предмете Высшая математика