Эконометрика УМП Каверина - 2011для эк и мен

НЕГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ВОСТОЧНАЯ ЭКОНОМИКО-ЮРИДИЧЕСКАЯ ГУМАНИТАРНАЯ АКАДЕМИЯ (Академия ВЭГУ)»

Кафедра «Управления и информатики»

УТВЕРЖДАЮ Проректор по учебной работе и инновационному развитию

__________ Р.Ф. Габидуллин «_____ »____________20___ г.

ЭКОНОМЕТРИКА

Учебно-методическое пособие

Составитель: к.ф.-м.н., доцент И.А. Каверина

Уфа 2011

Составитель: Каверина Ирина Александровна, кандидат физикоматематических наук, доцент.

Рецензент: Краснов Сергей Викторович, доктор технических наук, профессор, ВУиТ.

Пособие разработано в соответствии с государственным образовательным стандартом дисциплины «Эконометрика». Содержит необходимые сведения теоретического характера из разделов: регрессионный анализ, система одновременный уравнений, анализ временных рядов. Приводятся решения типовых примеров и задачи для самостоятельного решения. Рекомендуется для студентов очной и заочной форм обучения по направлению подготовки 080100 экономика (квалификация (степень) «бакалавр»).

Учебно-методическое пособие обсуждено и рекомендовано к изданию решением кафедры «Управления и информатики» протокол № 2 от « 28 » октября 2011 г.

Зав. кафедрой «Управления и информатики»

А.А. Руденко

Одобрена научно-методическим советом института «____»______________200 г., протокол №___

ВОСТОЧНАЯ ЭКОНОМИКО-ЮРИДИЧЕСКАЯ ГУМАНИТАРНАЯ АКАДЕМИЯ (Академия ВЭГУ), 2011

2

	Оглавление
Оглавление.........................................................................................................................................		3
1.	Построение уравнения регрессии.........................................................................................	4
2 Пример линейной регрессии..................................................................................................		6
3.	Системы эконометрических уравнений..............................................................................	13
4.	Проблема идентификации...................................................................................................	15
5.	Методы оценки параметров структурной формы модели.................................................	16
6.	Пример идентификации структурной модели....................................................................	17
7.	Моделирование одномерных временных рядов.................................................................	21
8.	Автокорреляция уровней временного ряда........................................................................	21
9. Алгоритм построения аддитивной или мультипликативной модели.................................		22
10.	Пример аддитивной модели временного ряда..................................................................	24
Вопросы к экзамену (зачету) ...................................................................................................		32
Таблица 1. Распределение Стьюдента.........................................................................................		35
Таблица 2. Распределение Фишера.............................................................................................		36

3

1. Построение уравнения регрессии

Постановка задачи. По имеющимся данным n наблюдений за совместным изме-

нением двух параметров x и y {(xi,yi), i=1,2,...,n} необходимо определить анали-

тическую зависимость yx f (x),	наилучшим образом описывающую данные на-
блюдений.
Линейная регрессия yx	a b x. Параметры а и b находятся из

следующей системы нормальных уравнений метода МНК:

a n b x y;

a x b x2 x y.

Можно воспользоваться готовыми формулами, которые вытекают из этой системы:

a

y

b

x

,

b

cov

x, y

,

(1)

2

x

______

____

где cov x,y y x

y

x

– ковариация

признаков x

и

y, x2 x2

x

2 –

дисперсия признака x и

1

x,

1

y,

______

1

y x,

____

1

x2 .

x

y

y x

x2

n

n

n

n

Парабола второй степени yx a b x c x2

приводится к линейному ви-

ду с помощью замены:

x x , x2 x

2

. В результате приходим к двухфакторному

1

уравнению y

x

a b x c x , оценка параметров которого при помощи МНК

1

2

приводит к системе следующих нормальных уравнений:

n

b x c x

2

y;

a

x

b x2 c x3 x y;

(2)

a

x2 b x3 c x4 x2 y.

a

4

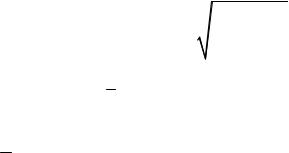
Тесноту связи изучаемых явлений оценивает линейный коэффициент

парной корреляции rxy

для линейной регрессии (–1 ≤ rxy ≤ 1)

r

b

x

cov x, y

,

xy

y

x y

и индекс корреляции xy

для нелинейной регрессии (0 ≤ xy ≤ 1)

2

xy

1

ост

,

2

y

где y2

1

y

y

2

–

общая

дисперсия результативного признака y,

n

ост2 1n y yx 2 – остаточная дисперсия.

Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака у характеризует коэффициент детерминации R2 rxy2

(для линейной регрессии) или индекс детерминации R2 xy2 (для нелинейной регрессии).

По коэффициенту (индексу) детерминации R2 можно судить о работоспособности (качестве) модели.

Правило 1. Если R2 0,75, то от модели следует отказаться. Если R2 0,75, то модель может использоваться для прогнозов.

Правило 2. Из двух моделей лучше та, у которой коэффициент детерминации больше.

Для оценки качества построенной модели можно также использовать среднюю ошибку аппроксимации:

yi

yx

1

n

1

n

A

Ai

100%.

i

n

n

y

i 1

i 1

i

Построенное уравнение регрессии считается удовлетворительным, если значение

A не превышает 10 %.

5

В экономических исследованиях широкое применение находит такой показатель, как коэффициент эластичности, вычисляемый по формуле

Ex(y) y' x y

Эластичность функции показывает приближенно, на сколько процентов изменится функция y f (x), при увеличении независимого аргумента x на 1%.

Для линейной функции y a b x производная равна y' b. Поэтому, для линейной зависимости между признаками коэффициент эластичности равен:

Ex(y) b x y

Средний коэффициент эластичности для линейной зависимости рассчитывается по формуле:

Ex (y) b x . y

2 Пример линейной регрессии

Задание I. Исследуется зависимость дохода Y от расходов на продукты питания X (в условных денежных единицах) по10 домохозяйствам.

Таблица 2.1

№ домохозяйства	Доход, Y	Расход на продукты питания, X
1	26	14
2	33	13
3	42	15
4	47	14
5	48	16
6	49	18
7	49	19
8	51	19
9	52	18
10	53	19

Требуется построить и проанализировать уравнение парной линейной

регрессии.

1. Постройте диаграмму рассеяния (поле корреляции) для результативного

признака Y и факторного признака X (таблица 2.1).

6

2. Рассчитайте уравнение парной линейной регрессии yx a b x и

сделайте оценки:

а) оцените тесноту связи с помощью коэффициента корреляции и коэффициента детерминации;

б) дайте с помощью среднего коэффициента эластичности оценку связи

фактора с результатом;

в) оцените качество уравнения с помощью средней ошибки аппроксимации;

г) оцените с помощью F - критерия Фишера для уровня значимости 0,05

статистическую надежность результатов регрессионного моделирования;

д) оцените с помощью

t- критерия

Стьюдента

для уровня значимости

0,05 статистическую значимость

коэффициента

регрессии

и

коэффициента

корреляции;

n

2

n

2

n

2

е) проверьте тождество

(yi y)

)

.

(yxi y)

(yi yxi

i 1

i 1

i 1

ж) используя графики отклонений (xi,ei) сделайте предположение о наличии гетероскедастичности.

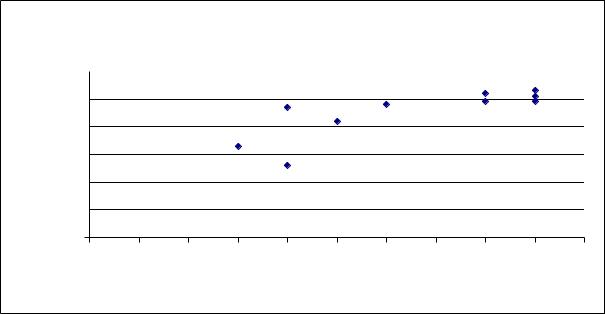
Решение. 1. При изучении зависимости между признаками графический метод подбора вида уравнения регрессии достаточно нагляден.

				Поле корреляции
	60
Y	50
	40
,
Доход	30
	20
	10
	0
	10	11	12	13	14	15	16	17	18	19	20
				Расход на продукты питания, X
			Рисунок 1.1 – Поле корреляции

7

Изобразим зависимость дохода Y домохозяйства от расходов на продукты питания X графически точками (xi,yi) координатной плоскости XOY , где xi -

расходы на продукты питания i- го домохозяйства, yi - его доходы, i 1,2,..,10

(рисунок 1.1). Такое изображение статистической зависимости называется полем корреляции. По расположению эмпирических точек можно сделать предположе-

ние о виде наличии линейной зависимости между переменными X и Y .

2. Для расчета параметров уравнения линейной регрессии, а также всех тре-

буемых показателей построим расчетную таблицу 1.1.

Таблица 1.1

1

2

3

4

5

6

7

8

9

10

11

				x						y				x2				y2								y x					y	x					(y					y		)2	(	y		y	)2	(y y	)2	A
				i								i		i						i							i i												i								xi			i	xi	i
																																i
1			14						26					196			676									364			37,62											361						54,41				135,11		44,71
2			13						33					169			1089									429			34,67											144						106,64				2,80		5,07
3			15						42					225			1764									630			40,57											9						19,59				2,03		3,39
4			14						47					196			2209									658			37,62											4						54,41				87,91		19,95
5			16						48					256			2304									768			43,52											9							2,18			20,03		9,32
6			18						49					324			2401									882			49,43											16						19,59				0,18		0,87
7			19						49					361			2401									931			52,38											16						54,41				11,40		6,89
8			19						51					361			2601									969			52,38											36						54,41				1,89		2,70
9			18						52					324			2704									936			49,43											49						19,59				6,63		4,95
10			19						53					361			2809									1007			52,38											64						54,41				0,39		1,18
Сумма			165					450					2773				20958									7574			450,00								708,00									439,62				268,38		99,03
Среднее			16,5						45				277,3				2095,8									757,4																										9,90
s2			5,05 70,80
s			2,25					8,41
Из таблицы 1.1 имеем:
																												2095,8;
		16,5;									45;				x2		277,3;										y2														757,4;
	x							y																														y x
	n							2							n										2
(yi				y)						708;										y)						439,62;
															(yxi
	i 1														i 1
	n																			1						n			1			n					y y
(yi										2															Ai												i			xi
				yxi				)				268,38;					A																											100% 9,90;
																					n									n									y
	i 1																								i 1							i 1							i
несмещенные оценки дисперсий:
			____
sx2 x2							x		2			277,3 16,52 5,05;																	sx				5,05						2,25;

8

____

s2y y2

y

2

2095,8 452 70,8; sy

8,41;

70,8

оценки параметров регрессии:

b

cov x, y

757,4 16,5 45

2,950;

a

y

b

x

45 2,950 16,5 3,683.

sx2

5,05

Итак, уравнение парной линейной регрессии имеет вид:

yx 3,683 2,950 x. (1)

Подставляя в уравнение (1) значения xi (ячейки столбца 2 таблицы 1.1),

найдем теоретические значения yxi (столбец 7 таблицы 1.1).

Полученное уравнение регрессии позволяет сделать вывод, что при увели-

чении расходов в домохозяйстве на 1 у.е., доходы домохозяйства увеличиваются в среднем на 2,950 у.е.

а) Тесноту линейной связи между признаками оценивает выборочный

коэффициент корреляции. По формуле

r b	sx	2,950	2,25	0,788.
xy	sy		8,415

Согласно количественной оценке тесноты линейной связи между признаками (таблица 1.2), между расходами на продукты домохозяйства и его доходами наблюдается сильная линейная связь.

Таблица 1.2 – Количественные критерии оценки тесноты линейной связи

Величина коэффициента корреляции r																Характер связи
	r		0,3													практически отсутствует
0,3							r						0,5			слабая
0,5						r						0,7				умеренная
0,7									r						1	сильная

Одной из наиболее эффективных оценок адекватности (соответствия)

регрессионной модели, мерой качества уравнения регрессии, является

коэффициент детерминации, определяемый по формуле:

9

	n
R2	(yxi			y		)2		439,62
	i 1									0,621.
	n
							708
	(yi		y		)2
	i 1
Это означает, что вариация							зависимой			переменной Y – дохода

домохозяйства – на 62,1% объясняется изменчивостью переменной X - расходами

на продукты питания, и на 37,9% объясняется изменчивостью других, неучтенных в модели факторов.

Коэффициент детерминации для линейной связи между признаками можно

вычислить иначе: R2 rxy2 0,7882 0,621. Получился тот же самый результат.

Такая проверка является контролем правильности выполнения арифметических

действий и выбора используемых формул.

Отметим, что чем ближе R2 к единице, тем лучше регрессия

аппроксимирует эмпирические данные, тем теснее наблюдения примыкают к

линии регрессии. Если		R2 1, то эмпирические точки		(xi, yi ) лежат на линии
регрессии и между переменными			X и Y существуют линейная функциональная
зависимость. Если	R2	0, то	вариация зависимой	переменной полностью

обусловлена воздействием неучтенных в модели переменных, и линия регрессии параллельна оси абсцисс.

б) Средний коэффициент эластичности равен:

Ex(y) b x 2,950 16,5 1,082. y 45

Полученное значение среднего коэффициента эластичности показывает, что при увеличении расходов на продукты питания на 1% от своего среднего значения x 16,5, доходы домохозяйства увеличиваются, соответственно, на

1,082% от своего среднего значения y 45.

в) Средняя ошибка аппроксимации является одной из оценок адекватности регрессионной модели, мерой качества уравнения регрессии.

Из таблицы 1.1 имеем A 9,90%. Полученное значение A говорит об удовлетворительной средней ошибке аппроксимации, не выходящей за

10