И.А. Паначев Рабочая программа, контрольные работы и методические указания по их выполнению для студентов заочной формы обучения (сокращенные сроки обучения на базе среднего проф. образования)

40

Полярный момент инерции относительно начала координат (полюса) (рис. 10.2) равен:

Iρ = ∫	ρ 2 dF.	(10.15)
F

Если через полюс проведена система взаимно перпендикулярных осей Х, Y, то ρ2 = х2 + y2 (рис. 10. 2) и, следовательно:

Iρ = Ix + Iy.

Центробежный момент инерции площади поперечного бруса относительно осей Х и Y (рис. 10.2.) равен:

Ixy = ∫X Y dF.

F

(10.16)

сечения

(10.17)

Осевые и полярные моменты инерции всегда положительны, а центробежный в зависимости от положения сечения относительно осей координат может быть положительным, отрицательным или равным нулю.

Центробежный момент инерции фигуры относительно осей, включающих хотя бы одну ось симметрии, равен нулю.

В самом общем случае переход от любой старой к любой новой системе координат может рассматриваться как два последовательных преобразования:

1) путём параллельного переноса осей координат Х, Y в новое положение X′, Y′

I

n

+ a

2F ),

(10.18)

x

′

= ∑(I

xi

i=1

i

i

I

n

+ b

2F ),

(10.19)

y

′

= ∑(I

yi

i=1

i

i

I

n

+a

b F ),

(10.20)

′

′ = ∑(I

x y

i=1

xiyi

i

i i

где Ixi, Iyi, Ixiyi – моменты инерции относительно центральных осей каждой из составляющих простейших фигур Fi; Ix′, Iy′, Ixy′ – моменты

инерции относительно новых осей; ai, bi – соответственно расстояния

от старых осей Х и Y до параллельных им новых осей Х′и Y′, которые в формулы (10.18), (10.19) и (10.20) входят со своими знаками;

					41
2) путём поворота осей на угол α								(10.21)
Iy′ = IxSin2α+IyCos2α+IxySin2α,								(10.22)
I	′ ′ = 0,5(I	x	− I	y	)Sin2α + I	xy	Cos2α.	(10.23)
	x y

10.4. Положение главных осей и величина главных моментов инерции

	Угол поворота одной из главных осей				относительно оси Х можно
	найти по формуле		2Ixy
	tg2α0	= −		.
			Ix −Iy		(10.24)

Положительный угол α0 откладывается против часовой стрелки, а отрицательный – по ходу.

Значения главных моментов инерции IU, IV можно найти по формуле

	IU,V = Imax,min =	Ix +Iy	±	1	(Ix −Iy )2	+4 I2xy .	(10.25)
		2		2

Ось максимумов всегда составляет меньший угол с той из осей (Х или Y), относительно которой осевой момент инерции имеет большее значение.

10.5. Последовательность (алгоритм) определения положения главных центральных осей инерции и величин главных центральных моментов инерции

10.5.1.В произвольной системе координат по формулам (10.11) и (10.12) определяем положение центра тяжести для составных (сложных) сечений, разбивая их на простые.

10.5.2.Через центр тяжести сечения проводим вспомогательные

центральные оси ХС и YC, параллельные осям системы координат простых фигур.

10.5.3.Затем по формулам (10.18), (10.19) и (10.20) определяем осевые и центробежные моменты относительно центральных осей ХС и YC.

42

10.5.4.По формуле (10.24) определяем угол α0 , характеризующий положение главных центральных осей инерции, и по формуле (10.25)- величину главных центральных моментов инерции.

10.5.5.После вычисления величин IU и IV рекомендуется проверить соблюдение равенства: +IV = IXc +IYc , (10.26)

а также равенство нулю центробежного момента инерции по фор-

муле (10.23).

10.6. Пример Для заданного на рис. 10.3 поперечного сечения, состоящего из

двутавра и равнобокого уголка, требуется: 1) определить положение центра тяжести; 2) найти осевые и центробежные моменты инерции относительно случайных осей, проходящих через центр тяжести (ХС и YC); 3) определить направление главных центральных осей (U и V); 4) вычертить сечение в масштабе 1 : 2 и указать на нём все размеры в числах и все оси, если дано: двутавр №22, уголок 90×90×7.

Решение Из сортамента выбираем необходимые данные. Для уголка равно-

бокого по ГОСТ 8509-72 b = 90 мм, d = 7	мм, z0 = 2,47 см,	F1 =
12,28 см2, Ix1 = Iy1 = 94,3 см4, Imax = 149,67	см4, Imin = 38,94 см4.

43

Для двутавра по ГОСТ 8239-72 h = 220 мм, b = 110 мм, d = 5,7 мм, F2 = 30,6 см2, Ix2 = 2550 см4, IY2 = 157 см4.

10.6.1. Проводим вспомогательную систему осей координат (Х, Y). Начало координат целесообразно расположить в центре тяжести какойлибо из фигур, например двутавра (чтобы сократить объём вычислений). Определяем координаты центра тяжести С всей фигуры в системе осей Х и Y:

Xc =

∑SYi

=

F1X1 + F2X2

= − 2,47 12,28

= −0,707см,

∑F

F

+ F

12,28 + 30,6

i

1

2

Yc =

∑Sxi

=

F1Y1 +F2Y2

=

13,47 12,28

=

3,86см,

12,28 +30,6

∑F

F +F

i

1

2

где

Y1 = h2 + Z0 = 222 +2,47 =13,47см, Y2 = 0,

X1 = −Z0 = −2,47см, X2 = 0.

Через центр тяжести С (рис. 10.4) проводим центральные оси ХС и YC параллельно проведённым ранее собственным осям уголка и дву-

тавра (Х1, Y1, Х2, Y2).

В системе координат центральных осей ХС и YC координаты центров тяжести уголка и двутавра определяем из выражения

ai = Yi − Yc , bi = Xi − Xc.

Данные сводим в табл. 11.

				Таблица 11
Точка	хi, см	yi, см	ai, см	bi, см
О1	- 2,47	13,47	9,61	- 1,76
О2	0	0	- 3,86	0,707

44

10.6.2. Вычисляем осевые и центробежные моменты инерции всего сечения:

Ixc = ∑(Ixi + ai2Fi ) = Ix1 + a12F1 + Ix2 + a22F2 =

=169,4 +9,612 12,28 + 2550 + (−3,86)2 30,6 = 4309,4см4 ,

Iyc = ∑(Iy1 + bi2F) = Iy1 + b12F1 + Iy2 + b22F2 =

=169,4 + (−1,76)2 12,28 +157 + 0,7072 30,6 = 305,46см4 ,

Ixcyc = ∑(Ixiyi + aibi Fi ) = Ix1y1 + a1b1F1 + Ix2y2 + a2b2F2 =

= 55,37 +9,61 (−1,76) 1228 + 0 + (−3,86) 0,707 30,6 = −236,19cм.

Рис. 10.4. Определение положения главных центральных осей инерции

45 Ix1y1 = 0, для равнобокого уголка

Ix1y1 =	Imax −Imin	=	149,67		−38,94	=55,37см	4	.
	2			2

Для неравнобокого уголка

Ixy = ±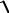 (Ix − Iu ) (I y − Iu ).

Знак центробежного момента инерции уголка определяем по следующему правилу (рис. 10.5.):

10.6.3. Находим угол α0 наклона главных центральных осей U и V относительно центральных осей ХС и YC:

	tg 2α0	= −	2I xcyc		=	2(−236,19)	= 0,1179,
			I xc	− I yc		4309,4 − 305,46

2α0 = arctg0,1179,

2α0 = 6o42′, α0 = 3o21′.

Поскольку угол α0 положительный, главная центральная ось U откладывается относительно оси ХС против часовой стрелки, а так как Ixc > Iyc, то ось U является осью, относительно которой момент инерции будет максимальным.

10.6.4. Вычисляем главные моменты инерции

	Imax,min =	Ixc + Iyc	±	1	(Ixc − Iyc )2 + 4 I2xcyc ,
		2		2

						46
Imax =Iu =	4309,4 +305,46		+		1	(4309,4 −305,46)		2	+4(−236,19)		2	= 4323,3см			4	,
	2				2
Imin = Iv =	4309,4 +305,46	−		1		(4309,4 −305,46)	2		+4(−236,19)	2		= 291,6см	4	.
	2			2

10.6.5. Проверка

Ixc + Iyc = Iu + Iv , 4309,+305,46 = 4323,3 + 291,6,

4614,86 = 4614,9.

Iuv = 0,5(Ixc −Iyc )sin 2α0 +Ixc cos2α0 =

=0,5(4309,4 −305,46)sin(6o42′) −236,19cos(6o42′) =

=234,63 −234,58 = 0.

11.ИЗГИБ ПРЯМЫХ БРУСЬЕВ

11.1. Общие понятия о деформации изгиба Изгиб представляет собой такую деформацию, при которой в попе-

речных сечениях стержня возникают изгибающие моменты, т.е. внутренние моменты, плоскость действия которых перпендикулярна плоскости поперечного сечения стержня.

Изгиб называется чистым, если изгибающий момент является единственным внутренним усилием, возникающим в поперечном сечении стержня.

В случае, когда в поперечном сечении наряду с изгибающим моментом возникает поперечная сила, изгиб называется поперечным.

Если плоскость действия сил (силовая плоскость) проходит через одну из центральных главных осей поперечного сечения стержня, изгиб называется простым или плоским (применяется также название прямой изгиб).

11.2. Определение внутренних усилий при изгибе На основании метода сечений можно записать, что:

а) поперечная сила Q в любом произвольном сечении балки численно равна алгебраической сумме проекций на плоскость сечения (ось Y) всех внешних сил, действующих по одну сторону от сечения :

Q = ∑Piy(пр) = ∑Piy(лев) ,	(11.1)

47

б) изгибающий момент в любом произвольном сечении балки численно равен алгебраической сумме моментов (вычисленных относительно центра тяжести сечения) внешних сил, действующих по одну сторону данного сечения :

М = ∑mx (Pi )(пр)

= ∑mx (Pi )(лев).

(11.2)

11.3. Правило знаков для изгибающих моментов и поперечных сил

Поперечная сила считается положительной, если равнодействующая внешних сил слева от сечения направлена снизу вверх, а справа – сверху вниз (рис. 11.1,а), и отрицательной – в противоположном случае

(рис. 11.1,б).

Рис.11.1. Правила знаков поперечной силы при изгибе

Изгибающий момент в сечении балки считается положительным, если равнодействующий момент внешних сил слева от сечения направлен по часовой стрелке, а справа – против часовой стрелки (рис.11.2,а), и отрицательным – в противоположном случае (рис. 11.2,б)

Рис.11.2. Правило знаков изгибающего момента при изгибе

Из рис. (11.2) следует более удобное для запоминания правило знаков изгибающих моментов. Изгибающий момент считается положи-

48

тельным, если в рассматриваемом сечении балка изгибается выпуклостью вниз (рис. 11.2,а) и наоборот.

11.4. Построение эпюр поперечных сил и изгибающих моментов Построение эпюр Q и М выполняют в следующем порядке.

11.4.1. Определяют опорные реакции с помощью уравнений статики, например :

	∑Piz = 0,	(11.3)
	∑mA (Pi ) = 0,

где Z – ось балки; А, В – любые точки, лежащие на оси Z.

11.4.2.Балка разбивается на n участков. Границами участков будут сечения, в которых меняется характер нагрузки. Это сечения, где приложена сосредоточенная сила, пара сил, начинает или кончает действовать распределённая нагрузка.

11.4.3.Для каждого участка по формулам (11.1) и (11.2) составляют

вобщем виде выражения Q и М в зависимости от текущей координаты

Z.

11.4.4.Для характерных сечений определяют значения Q и М. Эта операция может быть выполнена без составления выражений (11.1), (11.2). В этом случае для построения эпюр Q и М используют правила контроля эпюр, основанные на дифференциальных зависимостях :

dQ	= −q,	dM	= Q.	(11.4)
dZ		dZ

11.4.5. С помощью значений Q и М, полученных в п.11.4.4, строят эпюры этих усилий.

11.5.Подбор сечения

11.5.1.На основании эпюры М определяем опасное сечение. Опасным сечением будет сечение, где изгибающий момент дости-

гает максимального значения по абсолютной величине │М│мак. 11.5.2. Определяют расчётный момент сопротивления сечения из-

гибу:				M				(11.5)
W	=					мак .
xp
				[σ]
11.5.3. Подбирают размеры сечения из условия
Wx ≥ Wxp ,								(11.6)

49

а) для прокатных профилей – по сортаменту; б) для непрокатных профилей – методом последовательных при-

ближений или путём выражения Wx сечения через некоторый параметр размеров сечения по формуле

W	= Ix .			(11.7)
x		Yмак

11.6. Пример

Для заданных двух схем балок (рис.11.3) написать выражения Q и М для каждого участка в общем виде, построить эпюры Q и М, найти

ММАК и подобрать:

а) для схемы (а) деревянную балку круглого поперечного сечения

[σ] = 8 МПа;

б) для схемы (б) стальную балку двутаврового поперечного сечения при

[σ] = 160 МПа.

11.6.1. Схема а. Для балки, приведённой на рис. 11.3,а, построить

эпюры Q и М методом уравнений, если дано: Р1 = 30 кН, Р2 = 20 кН, m1 = 15 кН.м, q1 = 5 кН/м, а = 2 м.

Решение А. Отбрасываем связи, заменив их действия реакциями, и составля-

ем уравнения равновесия (рис. 11.4,а), используя формулы (11.3).

∑mв = −Ya 2a +2m1 +2q1 a 1,5a +2P2 a −P1 a = 0, −Ya 4 +30 +10 2 3 +40 2 −30 2 = 0,

Ya = 27,5кН,