В.Д. Богатырев Моделирование течения жидкости при действии силы тяжести

1

ВВЕДЕНИЕ

Физические процессы, изучаемые горной наукой, отличаются большой сложностью и описываются системами дифференциальных уравнений, а также начальными и граничными условиями с большим числом переменных. Найти решения таких задач довольно трудно. Поэтому на практике большое значение приобретает применение методов физического моделирования и опытных исследований, с помощью которых можно получить численные значения искомых переменных, а затем подобрать уравнения, описывающие результаты опытов.

Для изучения влияния на процесс какой-либо одной величины остальные следует сохранять неизменными, однако из-за большого числа переменных добиться этого часто очень сложно. Кроме того, при этом нужно быть уверенным, что результаты, получаемые с помощью какойлибо установки (модели), можно перенести и на другие аналогичные процессы (образец). Эти проблемы позволяет решить теория подобия.

С помощью теории подобия ряд размерных физических величин можно объединить в безразмерные комплексы. При этом число этих комплексов меньше числа исходных величин. Эти комплексы можно рассматривать как новые переменные. В результате введения в уравнения, описывающие исследуемый процесс, безразмерных комплексов число величин под знаком искомой функции значительно сокращается, что упрощает изучение физического процесса. Таким образом, теория

подобия и, в частности, данная лабораторная работа являются теоретической базой эксперимента и практически необходимы при теоретических исследованиях.

3

Уравнения движения (1) и неразрывности (2) могут быть записаны и в векторной форме:

уравнение движения

Краевые условия в данной задаче могут содержать только скорость, которая задается на границе в виде уравнения, выражающего скорость как функцию координат точек границы. Если рассматривается течение жидкости внутри какого-либо аппарата, то границами потока следует считать его входное сечение, где имеют место управляемые краевые условия и поверхности твердых стенок, где существуют неуправляемые граничные условия. В случае неподвижных стенок V=0. Поскольку это условие автоматически соблюдается и в модели и в натурном образце, то задание краевых условий сводится лишь к заданию скорости на входном сечении изучаемого объекта. Приведем рассматриваемые уравнения и граничные условия к безразмерному виду. Для этого выберем масштабы приведения, в качестве которых целесообразно принимать величины, входящие в граничные условия. Для линейных величин выберем какой-либо характерный размер l0, например гидравлический радиус для скорости V0 . После масштабных преобразований

( x = l0X; y = l0Y; z = l0Z; v = V0V; ν =ν0N; p = p0P; g = g0G; ρ = ρ0R )

и подстановки новых значений в уравнения (1) и (2) получим соотношения между величинами, при которых уравнения (1) и (2), а также граничные условия будут приведены к безразмерному виду. Будем иметь

Из условий (5) можно получить три уравнения связи, которые содержат шесть масштабов. Следовательно, любые три из них, имеющие независимые размерности, можно выбрать, например l0, ρ0, g0, а остальные три определить из уравнений связи (5):

Используя соотношения (6), можно записать выражения для безразмерных величин, например безразмерный коэффициент вязкости

4

а ускорение свободного падения G = 1.

Из выражений (5) и (7) следует, что осуществление требования

Nм = Nн при условии, что жидкость в модели и образце одна и та же, возможно только тогда, когда размеры образца и модели одинаковы,

т.е. l0м = l0н, только в этом случае будут соблюдаться равенства по скоростям граничных условий в модели и образце.

2.3. Течение при отсутствии влияния силы тяжести

Этот процесс характеризуется отсутствием свободных поверхностей, т.е. имеет место напорное течение. В данном случае влиянием сил тяжести можно пренебречь по сравнению с влиянием остальных сил, действующих на элементарную частицу жидкости. На основании анализа дифференциальных уравнений (1) и (2) и граничных условий при отсутствии в уравнениях параметра g получим систему уравнений связи

Используя уравнения (8), можно показать, что для достижения подобия нужно на границах модели обеспечить распределение скорости V, тождественно одинаковое с тем, которое имеется в образце. Обычно результаты опытов при рассмотрении данного вида течения жидкости обрабатывают для установления эмпирических законов движения, переходя к усредненным по сечению значениям скоростей и давлений, и заменяют их значения критериями подобия Eu и Re для усредненных величин, т.е. получают зависимости вида

Eu=ψ( Re).

2.4. Вязкостный режим течения

Этот процесс характеризуется исчезающе малым влиянием инерционных сил по сравнению с влиянием сил трения и давления. В данном случае на основании анализа уравнений:

движения –

− gradP + µ 2V = 0 ;

неразрывности –

divV = 0

и граничных условий –

Vг = ϕ(lг);

5

получаем одно уравнение связи

P0 = µ0V0 , l0 l02

используя которое можно установить подобие двух потоков.

Для осуществления подобия необходимо на границах модели обеспечить распределение скорости V, тождественно одинаковое с тем, которое имеется в образце. Отсюда следует, что подобие может быть осуществлено независимо от размеров модели.

2.5. Инерционный режим течения

В этом случае силы трения настолько малы, что их влиянием по сравнению с влиянием сил инерции и давления на режим течения можно пренебречь. Уравнения значительно упрощаются:

движения –

VgradV = ρ1 gradP ;

неразрывности –

divV = 0

и граничных условий –

Vг = ϕ(lг).

После приведения уравнений к безразмерному виду получаем одно уравнение связи

V02 = P0 .

l 0

Следовательно, условия подобия будут те же, что и при вязкостном течении. Условие подобия может быть достигнуто независимо от размеров физической модели, которая, разумеется, должна быть геометрически подобна образцу.

Таким образом, при физическом моделировании гидродинамических процессов, механизм которых для нас недостаточно ясен, необходимо соблюдать динамическое подобие, как показано в примере.

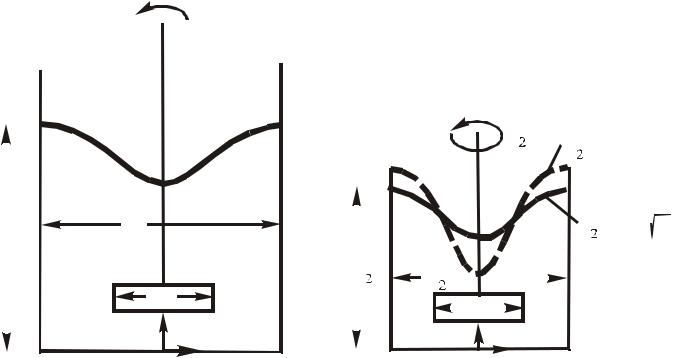
6

3. ПРИМЕР. Моделирование глубины центральной воронки в сосуде с мешалкой

Найти глубину центральной воронки при стационарном движении жидкости в большом резервуаре без отражательных перегородок (рис.1), заполненном маслом, как функцию скорости мешалки. Сделать это предполагается путем проведения модельных опытов в геометрически подобном сосуде меньших размеров. Поэтому определите условия, при которых следует осуществлять модельные испытания, чтобы обеспечить правильность предсказания результатов.

N1

Рис.1

Решение. Структура потоков в аппарате настолько сложна, что не допускает выполнения точных расчетов. Следовательно, нужно использовать методы теории подобия и анализа размерностей. Форма центральной воронки для любого сосуда с мешалкой будет одна и та же при одинаковых безразмерных уравнениях и безразмерных граничных условиях, описывающих течение. Дифференциальные уравнения (движения и неразрывности) мы уже рассмотрели. Граничные условия следующие:

7

Здесь S1(r, z) и S2(r, z) – поверхности воронки в большом и малом сосудах; Р0 – атмосферное давление. Можно также написать, что скорость относительно всех движущихся твердых поверхностей на этих поверхностях равна нулю.

Однако, указанных выше условий достаточно, чтобы наглядно показать метод, который собираемся применить. Пусть процесс протекает стационарно и начальные условия не нужны. В качестве стандартного линейного размера выберем диаметр турбинной мешалки D, а в качестве стандартного значения скорости – величину DN, равную произведению диаметра мешалки на скорость ее вращения в оборотах в единицу времени. Числа Рейнольдса и Фруда в данном случае принимают соот-

Теперь нетрудно убедиться, что для того, чтобы картины течения в двух сосудах с мешалками были подобны, должны выполняться следующие соотношения:

Первые два соотношения в (9) характеризуют условия геометрического подобия. Очевидно, что чем детальнее описание поверхности с нулевой скоростью, тем больше мы должны иметь таких геометрических соотношений. На практике могут оказаться существенными даже относительная шероховатость внутренних поверхностей резервуара и размеры головок болтов. Два последних соотношения в (9) устанавли-

8

вают требуемые соотношения между масштабными коэффициентами. Поскольку на практике менять гравитационное поле невозможно, из последнего соотношения (9) следует, что

Мы пришли к результату, что в данном случае динамическое подобие не может быть достигнуто при использовании в обоих сосудах одной и той же жидкости. Надо, чтобы в меньшем сосуде применялась менее вязкая жидкость. При линейных размерах малого аппарата, составляющих половину размеров большого аппарата, кинематическая вязкость в нем должна соответствовать кинематической вязкости масла

в большом аппарате, умноженной на 1 8 ≈ 0,35.

4. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Произвести разбор и усвоить изложенный материал. Выполнить по аналогии анализ подобия физической модели по натурному образцу на предложенном примере.

5. ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ ПО ГИДРОДИНАМИЧЕСКИМ РАСЧЕТАМ

На основании теории размерностей и подобия получена зависимость объема жидкости, протекающей через поперечное сечение трубы в единицу времени, от основных определяющих параметров:

где Р1 и Р2 – давление на входе и выходе из трубы соответственно; l – длина трубы; R – внутренний (гидравлический) радиус трубы; µ – динамическая вязкость жидкости или газа; С – коэффициент формы трубы (круглая, прямоугольная и т.д.).

Уравнение (10) справедливо для ламинарного (безвихревого) движения вязкой жидкости.

Пусть есть опытные данные по течению воды в трубе круглого се-

чения: Р1–Р2=5мПа; l=50 м; R=1м; Q=0,04м3/c. Определить для тех

же условий величины расходов для жидкостей или газов в вариан-

9

тах, указанных в таблице. Необходимые данные (динамическая вязкость) взять из справочников по физике.

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

1.Седов Л.И. Методы подобия и размерности в механике. – М.:

Наука, 1967. – 428 с.

2.Гухман А.А. Введение в теорию подобия. – М.:Высш. шк., 1973.

–296 с.