
6. Численное дифференцирование
Задача численного дифференцирования состоит в приближенном вычислении производной функции у=f(x) по заданным в конечном числе точек значениям этой функции.
6.1. Вычисление производной по ее определению
Пусть функция у=f(x) определена в окрестности точки х0 и имеет производную в этой точке, т.е. существует предел отношения приращения функции у к приращению аргумента х при х →0:
![]() (х0)=
(х0)=![]() (х0)=
(х0)=![]() ,
х=х-х0,
у=f(x0+х)-f(x0). (6.1)
,
х=х-х0,
у=f(x0+х)-f(x0). (6.1)
Значение производной в точке х0 можно получить, переходя к переделу в (6.1) по последовательности целых чисел п и полагая, например х=(х)п=(х)0/ап, (х)0 – некоторое начальное приращения аргумента, а – некоторое число (a>1), п =0, 1, …. Тогда значение производной в точке х0 можно записать:
![]() (х0)=
(х0)=![]() (х0)=
(х0)=![]() ,
(у)п=f(x0+(х)п)-f(x0), (6.2)
,
(у)п=f(x0+(х)п)-f(x0), (6.2)
отсюда
![]() (х0)
(х0)![]() . (6.3)
. (6.3)
Если функция у=f(x) в окрестности точки х0 имеет непрерывную производную до второго порядка включительно, то точность приближения производной соотношением (6.2) можно установить, воспользовавшись формулой Тейлора
![]() ,
,
Тогда
![]() .
.
И окончательно имеем
![]() ,
,
![]() . (6.4)
. (6.4)
При практических вычислениях производной с заданной точность удобно пользоваться формулой
![]() . (6.5)
. (6.5)
Пример 1. Вычислить производную функции y=sin x в точке х0=π/3 с точность ε=10-3 (π/3 =1,047198…).
Положим (х)=0,1; а=10; (х)п=0,1∙10-п, откуда
![]() .
.
Определим приближенное значение производной:
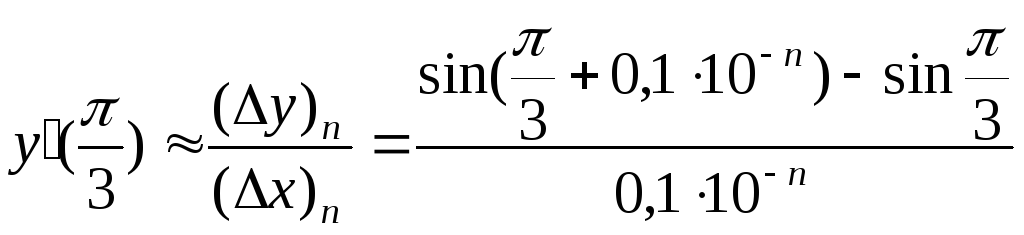 ;
п=0, 1, 2, …
;
п=0, 1, 2, …
Найдем отношения аппроксимирующие производную:
![]() 0,45590189;
0,45590189;
![]() 0,49566158;
0,49566158;
![]() 0,03975969;
0,03975969;
![]() =0,49956690;
=0,49956690;
![]() =0,00390532;
=0,00390532;
![]() =0,49995670;
=0,49995670;
![]() =0,00038979390
< ε.
=0,00038979390
< ε.
Итак,
начиная с третьего приближения, в
соответствии с оценкой (6.3), получаем
искомое приближение производной данной
функции
![]() с точностью, не менее чем заданная
ε=10-3.
с точностью, не менее чем заданная
ε=10-3.
6.2. Конечно-разностный аппроксимации производных
Пусть на отрезке [a, b] введена сетка h={xi=a+ih, i=0, 1, …, n, nh=b-a}, где h – шаг сетки, и определены значения функции уi=f(xi) функции у=f(x) в точках сетки. Выражения для первой производной функции в точке xi с помощью отношения конечных разностей можно записать следующим образом:
а) аппроксимация с помощью разностей вперед – правых разностей
![]() (хi)
(хi)![]() ,
хi=хi+1-хi=h,
уi=
yi+1-yi,
,
хi=хi+1-хi=h,
уi=
yi+1-yi,
![]() (хi)
(хi)![]() ,
i= 0, 1, …, n-1; (6.6)
,
i= 0, 1, …, n-1; (6.6)
Данное соотношение не позволяет вычислить производную в точке xn=b.
б) аппроксимация с помощью разностей назад – левых разностей
![]() (хi)
(хi)![]() ,
хi=хi-хi-1=h,
уi=
yi-yi-1,
,
хi=хi-хi-1=h,
уi=
yi-yi-1,
![]() (хi)
(хi)![]() ,
i= 1, …, n; (6.7)
,
i= 1, …, n; (6.7)
Данное соотношение не позволяет вычислить производную в точке x0=а.
в) аппроксимация с помощью центральных разностей (в этом случае рассматриваются три точки хi+1, хi, хi-1)
![]() (хi)
(хi)![]() ,
хi=хi+1-хi-1=2h,
уi=
yi+1-yi-1;
,
хi=хi+1-хi-1=2h,
уi=
yi+1-yi-1;
![]() (хi)
(хi)![]() ,
i= 1, …, n-1 (6.8)
,
i= 1, …, n-1 (6.8)
Аппроксимация с помощью центральных разностей представляет собой среднее арифметическое соотношений (6.6) и (6.7) в точках {xi}, i= 1, …, n-1. Кроме того, оно не позволяет вычислить значения производной в крайних точках интервала x0=а и xn=b.
Для функции у=f(x), имеющей непрерывную производную до второго порядка включительно, погрешность аппроксимации производных разностями вперед (6.6) и назад (6.7) в точке xi имеет один и тот же порядок О(h).
Рассмотрим левую разность
![]() .
.
По формуле Тейлора
![]() ,
,
следовательно
![]() .
.
Погрешность
![]() =
=![]() ;
[xi-h,
xi]
или [xi,
xi+h],
возникает при замене дифференциального
выражения
;
[xi-h,
xi]
или [xi,
xi+h],
возникает при замене дифференциального
выражения
![]() разностным yx,i
и называется погрешностью аппроксимации.
разностным yx,i
и называется погрешностью аппроксимации.
Погрешность
аппроксимации центральными разностями
(6.8) для функции у=f(x),
имеющей непрерывную производную до
третьего порядка включительно, имеет
порядок О(h2):
![]() ,[xi-h,
xi+h],
т.е. центральная разность аппроксимирует
производную более точно.
,[xi-h,
xi+h],
т.е. центральная разность аппроксимирует
производную более точно.
Приближенное значение производной второго порядка в точке xi выражается через значения функции уi+1, уi, уi-1. Для этого представим вторую производную с помощью правой разности
![]() ,
,
а производные первого порядка - с помощью левых разностей
![]()
![]() ,
,
![]()
![]() ,
,
тогда
![]() ,
i= 1, …, n-1 (6.9)
,
i= 1, …, n-1 (6.9)
Погрешность
последней аппроксимации имеет порядок
О(h2),
![]() ,
[xi-h,
xi+h]
для у=f(x),
имеющей непрерывную производную до
четвертого порядка включительно на
отрезке [a, b].
Формула (6.9) позволяет вычислить значения
второй производной только во внутренних
точках отрезка
,
[xi-h,
xi+h]
для у=f(x),
имеющей непрерывную производную до
четвертого порядка включительно на
отрезке [a, b].
Формула (6.9) позволяет вычислить значения
второй производной только во внутренних
точках отрезка
