Анализ данных отчеты Катков / Практическая работа №1

Министерство образования и науки

Государственное образовательное учреждение высшего профессионального образования

«Сибирский государственный индустриальный университет»

ОЦЕНКА ЗАКОНА РАСПРЕДЕЛЕНИЯ ПО ЭКСПЕРИМЕНТАЛЬНЫМ ДАННЫМ

Методические материалы к выполнению практической работы №1 по дисциплине «Анализ и обработка данных» для студентов, обучающихся по специальности 080801 Прикладная информатика (в управлении)

Новокузнецк

2010

УДК 519.24: 681.3

О

Рецензент доктор технических наук, профессор кафедры информационных

технологий в металлургии СибГИУ С.Н. Калашников

О 37 Оценка закона распределения по экспериментальным данным: метод. указ. / Сост.: Т.В. Кораблина; Сиб. гос. индустр. ун-т. – Новокузнецк: СибГИУ, 2010 – 26 с.

Изложены основные теоретические и практические подходы и алгоритмы для оценки закона распределения случайной величины по экспериментальным данным.

Предназначены для студентов специальностей 080801 – Прикладная информатика (в управлении).

СОДЕРЖАНИЕ
ВВЕДЕНИЕ................................................................................................	4
Оценка закона распределения случайной величины на основе
опытных данных........................................................................................	6
1. Задача определения закона распределения случайной величины
по статистическим данным....................................................................	7
Задание 1 ...............................................................................................	16
2. Задача проверки правдоподобия гипотез.......................................	17
Задание 2 ...............................................................................................	20
ПРИЛОЖЕНИЕ.......................................................................................	21
СПИСОК ЛИТЕРАТУРЫ.......................................................................	26

3

ВВЕДЕНИЕ

Ряды данных временные, пространственные и пространственновременные являются объектами анализа уже достаточно давно. Так, скалярным временным рядом называется последовательность из L чисел, представляющих собой значения некоторой динамическое переменной x(t) с постоянным шагом ∆t в моменты времени x(ℓ)=x[t(ℓ)], причем t(ℓ)=t(0)+(ℓ 1)∆t; ℓ – номер отсчета временного ряда, ℓ=0, 1, 2, …, L. Ряды данных являются основным результатом экспериментов, как натурных, так и модельных.

Необходимость анализа и исследования одномерных и многомерных рядов наблюдений возникает в самых разнообразных областях науки и техники, таких, как экономика, медицина, биология, радиотехника, радиофизика, геофизика, физика атмосферы и океана, акустика, астрономия. В течении длительного времени к анализу рядов данных подходили с позиции математической статистики. Использовался соответствующий математический аппарат, включающий понятия последовательностей случайных величин, случайных процессов, статистических моделей. Были также выделены две основные задачи анализа рядов [1].

1. Задача идентификации. При ее решении делается попытка ответить на вопрос, каковы параметры системы, породившей данный временной ряд. Параметры могут быть различными – статистические распределения, параметры статистических моделей, спектральные свойства и т.п. Эти параметры могут помочь идентифицировать систему, т.е. отличить ее от других. Такие задачи могут возникать, например, в медицине, технической диагностике и других областях, где

4

необходимо отличить норму от различных патологий, не разрушая систему, а используя доступные измерению характеристики.

2. Задача прогноза. Она состоит в том, чтобы по данным наблюдений предсказать будущие значения параметров системы или всей системы в целом.

Именно статистика предложила первые подходы к решению этих задач. Математическая статистика – это наука, предметом которой является разработка методов регистрации, описания и анализа статистических экспериментальных данных, полученных в результате наблюдения массовых случайных явлений [2].

С приложениями анализа временных рядов тесно связаны такие понятия теории вероятностей и математической статистики, как

функция плотности вероятности, среднее, дисперсия и ряд других.

Пусть имеется несколько одинаковых генераторов шума, с выходом всех этих генераторов связывают вероятностную функцию плотности f(х, t), имеющую следующие характеристики. Вероятность того, что в определенный момент t0 выход q-го генератора сигналов xq(t0) лежит в интервале между значениями а и b, определяется интегралом

b
P{a ≤ xq (t0 ) < b} = ∫ f (x,t0 )dx .	(1)

a

Математическое ожидание любой функции от х, обозначаемое М[g(x)] (где g(x) – та функция, ожидание которой ищется), определяется следующим образом:

В частности, истинные или множественные,	(2)
	среднее и диспер-
сия задаются формулами
∞
m(t0 ) = ∫x(t0 ) f (x,t0 )dx	(3)
−∞
∞
d(t0 ) = ∫[x(t0 ) − m(t0 )]2 f (x,t0 )dx	(4)

−∞

Стандартным отклонением называют положительное значение квадратного корня из дисперсии.

Если случайный процесс является стационарным, то параметры т(t0) и d(t0) не зависят от времени, т.е. для произвольных t0 и t1

т(t0)= т(t1)= т, d(t0)= d(t1) = d.

Допущение об эргодичности позволяет заменить усреднение по ансамблю усреднением по времени. В примере с генераторами шума

5

все генераторы были совершенно одинаковыми, поэтому знания лишь одной случайной функции отдельного генератора было бы достаточно, чтобы по выходу одного из них определить статистические параметры для всех. Так, выражение для среднего можно заменить уравнением

m		= lim	1	∞ x(t)dt ,	(5)
	х	P→∞ 2P −∞∫

в котором временное усреднение ведется по одной траектории процесса. Подобное выражение для дисперсии имеет вид

d		= lim	1	∞[x(t) −m]2 dt = M (x2 ) −M 2	(x)	(6)
	х	P→∞ 2P −∞∫

Как сказано выше, свойство эргодичности позволяет заменять усреднения по множеству реализаций случайного процесса усреднениями по времени.

Выбор методов сбора и обработки данных наблюдений над случайными процессами зависит от того, какое явление представляет изучаемый процесс, и от целей, которые достигаются обработкой. В общем случае можно выделить пять основных этапов:

1)сбор данных;

2)регистрация;

3)подготовка;

4)оценивание основных свойств;

5)анализ.

Основное внимание при выполнении лабораторных работ будет уделено выполнению четвертого и пятого этапов.

Оценка закона распределения случайной величины на основе опытных данных

При сборе данных об объектах или системах различной природы чаще всего не известны вообще или известны только приблизительно законы их развития и функционирования, кроме того на измеряемые значения какого-либо параметра действуют различные факторы, они могут быть искажены нежелательными шумами, что приводит к определенным ошибкам при вычислениях параметров данных временного ряда. Поэтому отсчеты исследуемого ряда данных x(ℓ), ℓ=1, 2, …, L можно рассматривать как возможные значения некоторой случайно величины Х. В теории вероятностей дается следующее определение случайной величины. Случайная величина – это величина, кото-

6

рая в результате опыта, может принять то или иное значение, причем заранее неизвестно – какое именно. Случайная величина считается описанной полностью, если задан ее закон распределения. Закон распределения случайной величины – это всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.

При оценке закона распределения случайной величины ставятся следующие задачи:

Задача определения закона распределения случайной величины по статистическим данным.

Задача проверки правдоподобия гипотез.

Задача определения неизвестных параметров распределения.

1. Задача определения закона распределения случайной величины по статистическим данным

Пусть имеется ряд данных, отсчеты которого будем рассматривать как значения случайной величины Х, закон распределения которой неизвестен. Требуется определить этот закон. Одним из способов обработки имеющегося ряда данных – первичного статистического материала, является построение статистической функции распределе-

ния. Статистической функцией распределения F*(x) случайной вели-

чины Х называется частота события Х<х в данном статистическом материале:

F*(x)=P*(X<x)

(7)

Для нахождения значения статистической функции распределения при данном х следует посчитать число значений, в которых величина Х приняла значение, меньше чем х, и разделить на общее число L имеющихся значений случайной величины.

Статистической функцией распределения любой случайной величины представляет собой прерывную ступенчатую функцию, скачки которой соответствуют наблюденным значениям случайной величины и по величине равны частотам этих значений.

При увеличении объема ряда данных L, согласно теореме Бернулли, при любом х частота события X<x приближается к вероятности этого события. Следовательно, при увеличении L статистическая функция распределения F*(x) приближается к подлинной функции распределения F(x) случайной величины Х.

Построение статистической функцией распределения решает задачу описания экспериментального материала, но часто бывает более

7

удобно – в смысле наглядности – пользоваться статистическими характеристиками распределения, аналогичными плотности распределения случайной величины f(x). Для большей наглядности статистического материала строится так называемый «статистический ряд», а затем гистограмма.

Алгоритм ее построения следующий:

1.Диапазон изменения случайной величины х делится на q интервалов длины h;

2.Подсчитывается количество попаданий mi величины х в i-й ин-

тервал; i=1, 2, …, q;

3.Определяется частота попаданий величины х в i-й интервал

	ϕi =	mi	(8)
		L
			1.
	где L – объем исследуемой выборки; ∑

Таблица 1, в которой приведены интервалы в порядке их расположения вдоль оси абсцисс и соответствующие частоты называется

статистическим рядом.

Таблица 1 – Статистический ряд

Ii		[x1, x2]		[x2, x3]	…		[xi, xi+1]		…	[xq, xq+1]
φi		φ1		φ2			φi			φq
Ii	–	обозначение		i-го интервала; [xi, xi+1] – его границы;
	4. Строится столбиковая диаграмма, по оси абсцисс откладывается
значение величины х, а по оси ординат								– частота попадания величи-
ны в соответствующий интервал (рисунок 1).
		Например, если бросать кубик L раз и считать, сколько выпало
единиц – m1,			двоек – m2 и т.д., то если L достаточно велико, то вели-
чины φi будут стремиться к соответствующим вероятностям
					lim ϕ	(L) = p =1/ 6 .				(9)
					L→∞ i		i
		Аналогичным образом дело обстоит и для непрерывной величи-
ны					limϕi(L) = pq (h),					(10)
					L→∞

где рi(h) вероятность того, что случайная величина x попадет в i-й интервал длины h. Пусть у≡(i –1)ε+ε/2 – середина этого интервала. Зафиксируем точку у и будем уменьшать величину h. Мы будем получать вероятности р(у, h). Рассмотрим предел

8

	lim	p( p,h)	= p(y) ,	(11)
		h
	h→0

который будем называть плотностью вероятности. Другими словами, вероятность того, что величина х принадлежит интервалу длины h, с серединой в точке у, равна р(у)·h.

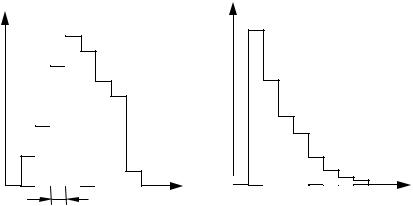
φi	φi
x	x
h
а)	б)

Рисунок 1 – Гистограммы для рядов данных

Визуальный анализ построенной гистограммы позволяет сделать предположение о том, какому закону распределения подчинена случайная величина. Так сравнивая гистограммы на рисунке 1 с теоретическими кривыми, приведенными на рисунках 2 – 7, можно видеть, что гистограмма на рисунке 1а схожа с нормальным распределением, а на рисунке 1б похожа на кривую экспоненциального распределения. Однако такое визуальное сравнение позволяет лишь предположить, какое теоретическое распределение наилучшим образом описывает экспериментальное, и не дает достаточных оснований, чтобы окончательно принять некоторую выдвинутую гипотезу. Аналитические выражения наиболее часто встречающихся законов распределения приведены ниже.

Равномерное распределение (рисунок 2):

1		приa ≤ x ≤ b
			(12)
f (x) = b −a
		при x < a, x > b
0

где ,

∞, ∞ – параметры.

9

Нормальное распределение или закон Гауса (рисунок 3):

1

−

(x−mx )2

2σ 2

∞

∞

f (x) = σ π e

где mx – математическое2ожидание; ,

σ – среднеквадратическое отклонение.

Экспоненциальное распределение (рисунок 4):

где λ – параметр, 0 < λ ≤f1.(x)=λe-λx,

0,∞

x [0,1],

β-распределение (рисунок 5):

где α, β > 0 – параметры,f (x) =

xα−1(1− x)β −1

,

B(α,β)

1

B(α,β) = ∫xα−1(1− x)β−1 dx – β-функция.

0

γ-распределение (рисунок 6):

−

x

e

f (x) = x

k

−1

θ

,

x [0,

∞)

Γ(k)θk

где k, θ > 0 – коэффициенты,

∞

Γ(k) = ∫xk −1e−x dx – γ-функция.

0

Распределение Пуассона (рисунок 7):

f (x) = e−λλk	, k={0, 1, 2, …}
k!

где λ > 0 – математическое ожидание.

Рисунок 2 – Равномерное распределение

10

(13)

(14)

(15)

(16)

(17)