DM.III

§ 11. Планарность графов

Для одного и того же графа можно построить различные геометрические реализации. В некоторых приложениях на реализации графов накладываются определенные ограничения, как это происходит, например, при разработке монтажных плат в радиоэлектронике. Микросхему, нанесенную на плоскую поверхность изоляционного материала способом травления или печати, можно рассматривать как геометрическую реализацию графа электрической цепи. Проводники на такой плате не изолированы, поэтому они не должны пересекаться. Возникает естественная задача: выяснить, можно ли изобразить на плоскости граф микросхемы так, чтобы на чертеже не было пересекающихся ребер. Если такое изображение построить не удается, печать микросхемы придется вести на нескольких платах. В этом случае важно найти наименьшее число возможных пересечений ребер графа электрической цепи при его изображении на плоскости и определить наименьшее количество плат, которое потребуется для печати микросхемы. Аналогичные задачи возникают при проектировании автомобильных трасс и железнодорожных путей, где также нежелательны развязки и переезды.

1. Укладки графов. Напомним понятие простой кривой. Пусть – трехмерное пространство или двумерная плоскость.

Простой незамкнутой кривой в U называется непрерывная кривая, соединяющая две различные точки в U и не имеющая точек самопересечения. Такая кривая гомеоморфна^ отрезку, т.е. непрерывно деформируется в отрезок.

Простой замкнутой кривой в U называется непрерывная самонепересекающаяся кривая, концевые точки которой совпадают. Такая кривая гомеоморфна окружности, т.е. непрерывно деформируется в окружность.

Плоским графом называется граф, вершины которого являются точками плоскости, а ребра – простыми кривыми, соединяющими соответствующие вершины так, что никакие два ребра не имеют общих точек, кроме инцидентной им обоим вершины.

Граф, изоморфный плоскому графу, называется планарным. Такой граф можно изобразить на плоскости так, что его ребра будут пересекаться только в вершинах. На рис. 137 показано, что полный граф является планарным.

Е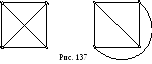 сли существует отображение вершин и ребер графа соответственно в точки и простые кривые плоскости , при котором различным вершинам соответствуют различные точки, а кривые, соответствующие различным ребрам, пересекаются только в точках, соответствующих концам этих ребер, то говорят, что граф укладывается на плоскости. Образ графа при таком отображении будем называть его правильной плоской укладкой. Аналогично определяется укладка графа в трехмерное пространство.

Оказывается, в трехмерном пространстве возможна геометрическая реализация любого конечного графа и даже графа со счетными множествами вершин и ребер. Более того, справедлива

Теорема 3.11.1. В трехмерном пространстве укладываются все те графы, множества вершин и ребер которых находятся во взаимно однозначных соответствиях с некоторыми подмножествами множества действительных чисел.

Следствие. Любой конечный граф или граф со счетным числом элементов имеет геометрическую реализацию в трехмерном пространстве.

Поэтому конечные графы, которые мы условились рассматривать, можно всегда наглядно представлять в виде пространственных геометрических графов.

Задача 11.1. Доказать, что любой простой конечный граф имеет укладку в пространство, ребра в которой являются прямолинейными отрезками.

Решение. Пусть простой граф имеет n вершин и m ребер (). Так как каждая пара вершин такого графа инцидентна не более чем одному ребру, то . Поставим в соответствие каждой вершине графа точку пространства так, чтобы эти точки находились в общем положении, т.е. никакие четыре из них не лежали в одной плоскости. Тогда любые две прямые, соединяющие пары из четырех различных точек, являются скрещивающимися и не имеют общих точек. Каждому ребру графа поставим в соответствие отрезок прямой, соединяющий соответственные точки пространства. Ясно, что граф, состоящий из n выбранных точек и m выбранных отрезков, является искомой укладкой графа .

Любой конечный граф можно каким-либо образом изобразить на плоскости, но не означает, что он укладывается на плоскость. В подавляющем большинстве случаев такое изображение будет «неправильным», т.е. некоторые ребра будут иметь пересечения в точках не являющихся вершинами графа. В общем случае, для заданного абстрактного графа не так-то просто решить проблему планарности, т.е. ответить на вопрос, изоморфен ли он плоскому графу.

Впервые критерий планарности графов в 1927 году доказал наш соотечественник Л.С.Понтрягин, но это доказательство не было опубликовано. В 1930 году тот же критерий был заново переоткрыт и опубликован польским математиком К.Кура-товским. Два года спустя еще один критерий планарности находит американский математик Х.Уитни. К настоящему времени получено еще несколько других критериев.

Перед рассмотрением этих критериев заметим, что можно рассматривать аналогичные задачи об укладке графов в различные геометрические пространства, в частности, об укладке графов на произвольных двумерных поверхностях. Еще одним направлением, имеющим важные практические приложения, является исследование вложений графов в другие графы. Подобные задачи возникают, например, в теории кодирования и при проектировании конечных автоматов.

2. Грани плоского графа. Теорема Эйлера. Рассмотрим конечный связный плоский граф . Область плоскости графа, ограниченная его ребрами и не содержащая внутри себя ни вершин, ни ребер, называется гранью^. Одна из граней плоского графа является внешней. Будем обозначать множество граней плоского графа через F, а для самого графа использовать обозначение .

Плоский граф на рис. 139 имеет 7 граней, грань f₃ является внешней. В этом примере грань f₁ ограничена всего одним ребром, грани f₆ и f₇ – двумя, f₂ и f₅ – тремя, f₄ – четырьмя, а внешняя грань f₃ ограничена 12 ребрами.

Примечание. Несмотря на кажущееся различие между внутренними и внешней гранями, их можно рассматривать как равноправные. Действительно, можно указать такое изоморфное отображение, при котором плоский граф G перейдет в плоский граф G, а внешняя грань графа G – во внутреннюю грань графа G. Для построения такого отображения обычно используется стереографическая проекция.

Основополагающим результатом в теории плоских графов является следующая теорема Эйлера.

Теорема 3.11.2. Пусть – связный плоский граф, имеющий вершин, ребер и граней. Тогда имеет место следующее равенство:

(3.11.1)

(формула Эйлера для плоского графа).

Доказательство. Будем удалять в заданном плоском графе ребра до тех пор, пока не получим суграфа, являющегося его остовым деревом. Каждое удаление ребра будет уменьшать количества граней и ребер на единицу, а величина будет оставаться неизменной. Следовательно, эта величина будет одинаковой как у исходного графа, так и у его остового дерева. Но у дерева и , поэтому . ■

Следствие 1. Для любого связного сферического графа справедлива формула Эйлера (3.11.1).

Действительно, при помощи отображения, обратного стереографической проекции, любой связный сферический граф отображается на связный плоский граф, для которого выполняется равенство (3.11.1).

Следствие 2. Для любого простого многогранника^ справедлива формула Эйлера (3.11.1).

Для доказательства этого факта можно деформировать поверхность многогранника в сферу (например, «раздуть») и применить формулу Эйлера для полученного сферического графа.

3. Двойственность плоских графов. Пусть на плоскости задан связный плоский граф G. Говорят, что грань h графа G инцидентна ребру а, если ребро а принадлежит границе грани h. Две грани графа называются смежными, если они инцидентны одному и тому же ребру.

Граф называется двойственным для плоского графа G, если выполняются два следующих условия:

1) каждой грани h графа G соответствует единственная вершина графа ;

2) если вершины и в соответствуют граням h₁ и h₂ в G, то каждому ребру а графа G, инцидентному граням h₁ и h₂, соответствует единственное ребро графа , инцидентное вершинам и .

Ясно, что двойственный граф существует для любого плоского графа G. Геометрически он может быть реализован следующим образом. В каждой грани графа G выберем по точке (залитые точки на рис. 142). Если ребро а в графе G инцидентно двум граням h₁ и h₂, то соответствующие точки и в соединим ребром (эти ребра изображены пунктирными линиями), пересекающим ребро а, и не пересекающим другие ребра графа G.

Заметим, что если ребро а графа G не принадлежит никакому циклу (т.е. является перешейком), то в графе ему соответствует петля (рис. 143).

Из определения двойственного графа следует, что граф , двойственный плоскому графу G, также является плоским. Более того, если построить двойственный граф для графа, двойственного графу G, то получится граф, изоморфный исходному графу G.

Пусть и – два взаимно двойственных плоских графа. Тогда имеют место следующие очевидные равенства:

.

П римечание. Два изоморфных плоских графа могут иметь неизоморфные двойственные графы. Так, графы G₁ и G₂ на рис. 144 изоморфны, но двойственные им графы и не изоморфны.

Действительно, граф имеет две вершины степени 5 и две вершины степени 3, а граф имеет две вершины степени 4, одну вершину степени 3 и одну вершину степени 5. Приведенный пример свидетельствует о том, что строение двойственного графа для заданного плоского абстрактного графа G существенно зависит от способа его геометрической реализации. Более того, можно показать, что если граф G₂ получается из графа G₁ при помощи непрерывной деформации плоскости, то граф , двойственный G₁, будет изоморфен графу , двойственному G₂. Очевидно, что графы G₁ и G₂, приведенные на рис. 144, не переводятся один в другой при помощи непрерывной деформации плоскости, поэтому двойственные им графы не изоморфны.

4. Графы из многоугольников. Плоский связный граф G называется графом из многоугольников, если каждая его грань ограничена не менее чем тремя ребрами, и каждое ребро является инцидентным двум граням. Так, например, плоский граф, изображенный на рис. 145, является графом из многоугольников. Граф на рис. 146 таковым не является по следующим причинам: во-первых, в нем есть петля, ограниченная одним ребром и грань, ограниченная двумя ребрами, во-вторых, одно из ребер графа является перешейком и, значит, инцидентным всего одной грани (внешней).

Т ак как граф из многоугольников не может иметь петель, параллельных ребер и перешейков, то его можно определить иначе: графом из многоугольников называется простой связный граф без перешейков.

Для плоских графов без перешейков любое ребро всегда инцидентно двум граням. Для таких графов (в частности, для графов из многоугольников) справедлива следующая теорема, двойственная теореме 3.1.1.

Теорема 3.11.3. В любом плоском графе без перешейков количество граней, ограниченных нечетным числом ребер, – четно.

Доказательство. Обозначим через количество ребер, ограничивающих грань h. Так как по условию теоремы каждое ребро графа инцидентно ровно двум его граням, то сумма всех ребер, ограничивающих все грани, равна удвоенному числу ребер графа:

. (3.11.2)

Сумма, входящая в левую часть формулы (3.11.2), есть четное число, поэтому в нее может входить лишь четное число нечетных слагаемых. ■

Следствие. Сумма всех ребер, ограничивающих все грани плоского графа без перешейков, равна удвоенному числу его ребер.

Теорема 3.11.4. Любой плоский граф, степень каждой вершины которого не меньше трех (в частности, любой выпуклый многогранник), содержит грань, ограниченную менее чем шестью ребрами.

Для графов из многоугольников справедливы следующие свойства.

1º. Для любого графа из многоугольников имеет место неравенство:

. (3.11.3)

Действительно, для любой грани h рассматриваемого графа можно записать . Следовательно, используя формулу (3.11.2), получим: .

2º. Для любого графа из многоугольников справедливо неравенство:

. (3.11.4)

В самом деле, из формулы Эйлера для плоского графа следует, что . Подставляя найденное для f выражение в неравенство (3.11.3), последовательно получим:

.

Графы из многоугольников, каждая грань которых ограничена одним и тем же числом ребер (т.е. для каждой грани h), называются графами из r-угольников. Граф, двойственный графу из r-угольников, является однородным графом степени r.

Для графа из r-угольников справедливы следующие равенства, вытекающие из формул (3.11.2) и (3.11.1):

, (3.11.5)

. (3.11.6)

Граф из треугольников называется плоской триангуляцией. Для плоской триангуляции неравенства (3.11.3) и (3.11.4) трансформируются в равенства. Поэтому число ребер и число граней плоской триангуляции с вершинами вычисляются по формулам:

, (3.11.7)

. (3.11.8)

Важность этого класса плоских графов демонстрирует следующая теорема.

Теорема 3.11.5. Любой простой плоский граф, содержащий не менее трех вершин, является суграфом некоторой плоской триангуляции с тем же числом вершин.

Задача 11.4. Доказать, что существует ровно пять типов правильных многогранников.

Решение. Простой многогранник является топологически правильным, если из каждой его вершины выходит одинаковое количество ребер, и все его грани ограничены одинаковым числом ребер. Это означает, что степень каждой вершины соответствующего плоского графа такого многогранника равна постоянному числу , а степень каждой вершины двойственного графа также равна постоянному числу .

Используя формулы (3.1.1) и (3.11.2), можно записать: или Подставляя эти выражения в формулу Эйлера (3.11.1), получим, что .Последнее равенство можно записать в виде: . Следовательно,

, .

Так как количества ребер, граней и вершин выражаются натуральными числами, то приходим к неравенству

,

которое можно переписать в виде

.

Это неравенство дает всего пять решений для и , каждому из которых соответствует один тип правильного многогранника (см. табл. 11).

					Многогранник
3	3	4	6	4	тетраэдр
3	4	8	12	6	октаэдр
3	5	20	30	12	икосаэдр
4	3	6	12	8	гексаэдр (куб)
5	3	12	30	20	додекаэдр

Табл. 11

5. Критерии планарности. В учебной литературе при рассмотрении критериев планарности графов стало традицией начинать изложение с двух следующих задач:

1. Можно ли соединить дорожками 5 домов так, чтобы дорожки не пересекались, и каждая пара домов была соединена одной дорожкой?

2 . В трех домах живут трое враждующих соседей, каждый из которых ходит за водой в один из трех колодцев. Можно ли протоптать тропинки от каждого дома к каждому колодцу таким образом, чтобы пути соседей не пересекались?

Очевидно, что первая задача моделируется с помощью полного графа (рис. 147), вторая – с помощью полного двудольного графа (рис. 148), а чтобы ответить на поставленные в задачах вопросы, нужно выяснить, являются ли эти графы планарными. Согласно определению планарного графа необходимо выяснить, существует ли геометрическая реализация этих графов, являющаяся плоским графом. Докажем, что в обеих задачах ответ на вопрос – отрицательный.

Полный граф имеет вершин и ребер. Если бы этот граф был плоским, для него выполнялось бы неравенство (3.11.4) . Однако . Поэтому граф не является плоским и поэтому – планарным.

В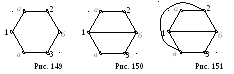 о второй задаче попытаемся изобразить граф на плоскости так, чтобы его ребра пересекались только в общих вершинах. На любой такой геометрической реализации графа должен быть представлен цикл 1, а, 2, б, 3, в; изобразим этот цикл в виде выпуклого шестиугольника (рис. 149). Цикл-шестиугольник имеет две грани – внутреннюю и внешнюю.

Осталось изобразить ребра (1, б), (2, в) и (3, а). Любое из этих ребер можно провести либо во внутренней грани, либо во внешней. Если, например, ребро (1, б) изобразить во внутренней грани (рис. 150), то ребро (2, в) придется проводить во внешней грани (рис. 151). Но тогда оставшееся ребро (3, а) невозможно нарисовать так, чтобы оно не пересекало уже нарисованных ребер. Следовательно, граф также не является планарным.

Таким образом, доказана

Теорема 3.11.6. Графы и не являются планарными.

Рассмотренные графы играют важную роль при распознавании планарных графов. Их часто называют графами Понтрягина-Куратовского, по имени математиков, впервые доказавших необходимый и достаточный признаки планарности графов. Прежде чем познакомиться с этим критерием планарности, введем понятие гомеоморфных графов.

Гомеоморфизм графов определяется с помощью понятия измельчения графа. Напомним, что граф называется измельчением (подразбиением) графа , если его можно получить из графа в результате последовательного применения операции измельчения ребер.

Очевидно, что свойство планарности сохраняется, если некоторое ребро графа разбить на два введением новой вершины второй степени, или, наоборот, заменить два ребра, инцидентных одной вершине второй степени, одним ребром, удалив эту вершину.

Два графа и называются гомеоморфными, если у них существуют изоморфные измельчения. Иными словами, два графа являются гомеоморфными (или изоморфными с точностью до вершин второй степени), если заменой некоторых их ребер простыми цепями графы преобразуются в изоморфные графы.

Например, графы на рис. 152 гомеоморфны. Измельчения ребер, позволяющие установить этот гомеоморфизм, показаны на рис. 153.