DM.III

§ 9. Подмножества множества вершин графа

1. Доминирующие множества вершин. Покрытия. Пусть – произвольная вершина графа . Множество вершин графа , смежных , называется окружением этой вершины и обозначается . Аналогично определяется понятие окружения любого подмножества множества вершин . А именно, окружением подмножества в графе называется подмножество вершин , определяемое как

.

Н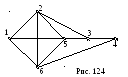апример, для графа на рис. 124 окружение подмножества есть .

Подмножество называется доминирующим множеством для графа , если каждая не принадлежащая вершина является концом некоторого ребра, другой конец которого лежит в . Другими словами, подмножество называется доминирующим, если его окружение есть .

Доминирующее множество графа называется минимальным, если оно не содержит подмножеств, являющихся доминирующими множествами этого графа. Минимальное доминирующее множество, содержащее наименьшее возможное число элементов, называется наименьшим доминирующим множеством. Число вершин, входящих в наименьшее доминирующее множество графа , называется числом доминирования; обозначим его .

Для графа на рис. 124: , , – его доминирующие множества. При этом множество не является минимальным, т.к. . Множества , не имеют собственных подмножеств, являющихся доминирующими множествами графа, поэтому они являются минимальными доминирующими множествами графа . В графе нет доминирующих множеств, состоящих менее чем из двух вершин. Поэтому для рассматриваемого графа .

Доминирующие множества часто возникают в задачах, связанных с настольными играми. Многие из таких игр можно представить с помощью графов, в которых вершины соответствуют позициям, а ребра – ходам. В таком графе доминирующее множество – такое множество позиций, из которых за один ход можно попасть во все остальные позиции.

Задача 9.1. Расставить на шахматной доске минимальное число ферзей так, чтобы они держали под боем каждую клетку доски.

Ферзь может ходить на любое число клеток по горизонтали, вертикали и диагонали. Поэтому он одновременно угрожает всем клеткам, лежащим на горизонтали, вертикали и диагоналях, на пересечении которых расположен. Клетки доски примем за вершины графа, две клетки связаны ребром, если ферзь, поставленный на одну из клеток, угрожает другой. На языке введенных понятий в задаче требуется найти наименьшее доминирующее множество. Оказывается, для решения задачи достаточно 5 ферзей (одно из возможных решений показано на рис. 125). Следовательно, для графа этой задачи .

Задача 9.2. Во время научной конференции выяснилось, что один из четырех ее любых участников встречался ранее с тремя остальными. Доказать, что среди любых четырех участников конференции всегда можно найти такого, который встречался ранее со всеми участниками конференции.

Решение. Сопоставим участникам конференции вершины графа , и вершины, соответствующие ранее встречавшимся участникам, соединим ребром. Из условия задачи следует, что число вершин этого графа не меньше 4. Требуется доказать, что .

При решении подобных задач удобно перейти к графу , являющемуся дополнением графа . В графе ребрами соединяются только вершины, соответствующие не встречавшимся ранее участникам конференции. Сама исходная задача эквивалентна задаче:

Пусть среди () вершин графа нельзя найти четыре такие, каждая из которых была бы соединена по меньшей мере с одной из трех остальных вершин. Доказать, что тогда среди любых четырех вершин графа найдется такая, которая не соединена ребром ни с одной из остальных вершин.

Случай, когда граф является безреберным, очевиден. Если граф имеет всего одно ребро, то из всех его вершин, за исключением, быть может, двух, не будет выходить ни одного ребра и среди любых четырех вершин найдется такая вершина, из которой не выходит ни одного ребра. Поэтому естественно считать, что в графе всегда найдутся по крайней мере два ребра и . Далее, если предположить, что эти два ребра несмежны, то их концы не будут удовлетворять условию задачи. Следовательно, ребра и должны быть смежными. Наконец, в графе может быть только одно ребро , имеющее по крайней мере один общий конец с ребрами и . Действительно, если предположить противное, снова получим противоречие с условием задачи.

Возможны три случая: 1) ребро инцидентно общему концу ребер и (рис. 126); 2) ребро инцидентно одному из несовпадающих концов ребер и (рис. 127); 3) ребро соединяет несовпадающие концы ребер и (рис. 128).

П ервый случай отпадает, т.к. существование вершины, из которой выходит 3 ребра противоречит условию. Во втором случае каждая из вершин соединена по меньшей мере с одной из трех остальных вершин, что снова противоречит условию. Таким образом, остается случай, представленный на рис. 128. Тем самым доказано, что какие бы четыре вершины мы ни выбрали, среди них обязательно найдется по крайней мере одна, не соединенная ребрами ни с какой другой вершиной графа. Это означает, что в графе найденная вершина, наоборот, будет соединена ребрами со всеми остальными вершинами, т.е. .

Теорема 3.9.1. Число доминирования графа , имеющего вершин, удовлетворяет неравенству

, (3.9.1)

где – наибольшая из степеней вершин графа.

Доказательство. Пусть – наименьшее доминирующее множество графа . Объединение вершин из и вершин, смежных с ними, есть множество всех вершин графа. Поэтому

.

Следовательно, неравенство (3.9.1) верно. ■

Для графа на рис. 124 множества , являются покрытиями. Если из покрытия удалить вершину 1, оставшееся множество вершин по-прежнему будет покрытием графа , значит, это покрытие не является минимальным. Покрытие – минимальное и, кроме того, наименьшее. Следовательно, .

Легко проверить, что , , , а для графа, имеющего две компоненты связности и : .

2. Независимые множества вершин. Груды и клики графа. При решении задач с помощью графов приходится также определять максимальное число попарно несмежных вершин; в этом случае полезны следующие понятия.

Пусть – граф без петель. Множество вершин графа называется независимым (или грудой графа), если никакие две вершины из этого множества не смежны. Другими словами, груда графа – безреберный подграф этого графа, не являющийся его суграфом. Множество вершин графа называется зависимым, если в нем хотя бы две вершины соединены ребром. Множество вершин графа называется полностью зависимым, если каждая пара его вершин соединена ребром. Очевидно, что вершины полностью зависимого множества являются вершинами полного подграфа графа .

Груду графа, содержащую m вершин, кратко называют его m-грудой. Груду графа , имеющую наибольшее число вершин среди всех его груд, называют наибольшей грудой или наибольшим независимым множеством графа. Число вершин, содержащихся в наибольшей груде графа, называется вершинным числом независимости (или неплотностью) этого графа и обозначается .

Очевидно, что , , , а для графа, имеющего две компоненты связности и : .

Задачей об отыскании наибольшей груды графа является следующая известная шахматная задача.

Теорема 3.9.2. В графе , имеющем вершин и ребер, вершинное число независимости удовлетворяет неравенствам

, , (3.9.2)

где – наибольшая, а – наименьшая из степеней вершин графа.

Доказательство. Пусть – наибольшая груда графа . Первое неравенство доказывается аналогично неравенству (3.9.1). Для доказательства второго неравенства заметим, что из каждой вершины графа выходит не менее ребер. Поскольку никакие две вершины в наибольшей груде не смежны, то . Откуда вытекает доказываемое неравенство. ■

Задача 9.5. Городская администрация решила расположить городские аптеки на перекрестках города так, чтобы на любых двух соседних перекрестках находилось не более одной аптеки. Для этой цели было запланировано выделение средств на оборудование 40 аптек. Известно, что в городе 150 участков улиц между перекрестками и на каждом перекрестке сходится не менее четырех улиц. Можно ли сэкономить средства городского бюджета, оборудовав менее 40 аптек, не нарушая при этом начальные требования по их расположению?

Решение. Рассмотрим граф , вершинами которого служат перекрестки, а ребрами – участки улиц между ними. По условию на каждом перекрестке сходится не менее четырех улиц, поэтому . Поскольку нельзя располагать аптеки на соседних перекрестках, то перекресткам, на которых будут располагаться аптеки, должно соответствовать независимое множество вершин графа. В силу теоремы 3.9.2 , поэтому в городе можно установить не более 37 аптек и тем самым добиться экономии бюджетных средств.

Рассмотрим связь между числами доминирования, покрытия и вершинным числом независимости графа.

Теорема 3.9.3. Независимое множество вершин графа является наибольшей грудой тогда и только тогда, когда оно доминирующее.

Доказательство. Пусть – наибольшая груда графа , тогда в не может быть вершин, не соединенных ребром с вершинами из . Действительно, если такая вершина существовала, наибольшей грудой было бы множество , что противоречит условию. Поэтому – доминирующее множество.

Обратно, пусть – независимое доминирующее множество вершин. Тогда любая вершина из соединена по крайней мере с одной вершиной из . Следовательно, независимое множество является наибольшим. ■

Следствие. Вершинное число независимости не может быть меньше числа доминирования, т.е.

. (3.9.3)

Теорема 3.9.4. Подмножество множества вершин графа является наименьшим покрытием тогда и только тогда, когда множество остальных вершин графа является наибольшей грудой этого графа, т.е.

, (3.9.4)

где – число ребер графа.

Доказательство. По определению множество является грудой графа тогда и только тогда, когда в графе нет ребер, оба конца которых содержатся в . Поэтому один конец каждого ребра лежит в , т.е. – покрытие . Поскольку для любой груды , то наименьшему покрытию соответствует наибольшая груда и наоборот. ■

Задача 9.6. Автоинспекция для наблюдения за порядком на улицах города собирается установить телекамеры на его перекрестках. Каждая телекамера контролирует перекресток, на котором она установлена, все улицы, выходящие из этого перекрестка, включая и соседние перекрестки. Сколько нужно установить телекамер, если в городе 75 перекрестков, а наибольшее число телекамер, которые можно установить так, чтобы ни одна из них не наблюдала за другой, равно 30?

Решение. Вновь рассмотрим граф , вершинами которого служат перекрестки, а ребрами – участки улиц между ними. Искомое число телекамер будет равно числу покрытия графа . По условию , . Следовательно, .

В тех случаях, когда, наоборот, требуется найти наибольшее число попарно смежных вершин графа, вводится понятие клики. Клика – полностью зависимое множество вершин графа. Клика, содержащая r вершин, называется r-кликой.

Клику графа , имеющую наибольшее число вершин среди всех его клик, называют наибольшей кликой графа , а число ее вершин, обозначаемое , – плотностью этого графа.

Пусть – дополнение графа порядка до полного графа . Как было отмечено в § 3 этой главы, две несовпадающие вершины смежны в тогда и только тогда, когда они не смежны в . Поэтому кликам графа в его дополнении соответствуют груды и наоборот. Из определений неплотности и плотности графа следует, что и .

Ч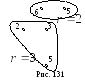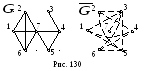тобы продемонстрировать изложенное, рассмотрим граф на рис. 130 и его дополнение .

На рис. 131 даны примеры груд графа , из них 3-груда, образованная вершинами 2, 3, 5, является наибольшей, поэтому неплотность этого графа равна 3.

Н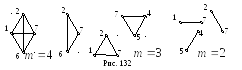 а рис. 132 приведены примеры клик графа , наибольшей из которых является клика, покрывающая граф и содержащая вершины 1, 2, 7, 6. Поэтому плотность графа равна 4.

Наконец, на рис. 133 показаны максимальная груда и одна из максимальных клик графа . Видим, что и .

З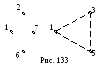аметим, что поиски в произвольных графах доминирующих множеств, покрытий, наибольших груд и клик являются важными и сложными задачами, которые часто возникают в различных прикладных задачах. Для решения этих задач используются различные алгоритмы перебора, а в некоторых случаях – их улучшенные варианты.

§ 10. Двудольные графы. Паросочетания

1. Покрывающие и независимые множества ребер. Паросочетания. Реберное покрытия графа определяется по аналогии с вершинным. Пусть имеется граф . Множество ребер графа называется реберным покрытием графа, если каждая вершина графа является концевой для некоторого ребра из множества .

Покрытие называется минимальным, если после удаления из него любого ребра оно перестает быть покрытием. Реберное покрытие графа , содержащее наименьшее число ребер среди всех его реберных покрытий, называется наименьшим, а число его ребер – числом покрытия.

Легко проверить, что:

1) , , где , – циклы с четным и нечетным числом вершин соответственно;

2) , ;

3) .

Паросочетанием (или независимым множеством ребер) в графе называется подмножество ребер из , в котором каждая пара ребер не имеет общей вершины. Другими словами, паросочетание – произвольное множество попарно несмежных ребер графа.

Паросочетание называется максимальным, если к нему нельзя добавить ни одного ребра так, чтобы полученное множество ребер осталось паросочетанием. Паросочетание графа , содержащее наибольшее число ребер среди всех его паросочетаний, называется наибольшим, число его ребер называется реберным числом независимости этого графа и обозначается .