
DM.III.6n
.doc
![]() ,
называется взвешенным
центром
этого графа и т.д.
,
называется взвешенным
центром
этого графа и т.д.
Примечание.
При определении взвешенного графа мы
ограничились весовыми функциями,
принимающими неотрицательные
действительные значения. В некоторых
приложениях приходиться рассматривать
весовые функции
![]() ,
,
![]() ,
где
,
где
![]() ,
,
![]() – произвольные множества. Наиболее
часто встречаются взвешенные графы
– произвольные множества. Наиболее
часто встречаются взвешенные графы
![]() и орграфы
и орграфы
![]() ,
у которых
,
у которых
![]() .
.
§ 8. Экстремальные задачи
во взвешенных графах
Как отмечалось, наиболее часто областью приложений взвешенных графов являются дискретные экстремальные задачи. С помощью взвешенных графов исследуются не только различные сети коммуникаций, но и электрические схемы, структурные формулы химических соединений, сетевые графики и т.п. Алгоритмам решения подобных задач посвящена многочисленная учебная и научная литература. Поэтому ограничимся описанием алгоритмов решения наиболее типичных задач, важных для приложений.
1.
Максимальный
поток в сети.
Понятия сети и потока в сети возникают
в приложениях взвешенных графов к
анализу систем транспортировки каких-либо
продуктов (электроэнергии, нефтепродуктов,
товаров и т.п.) из одного пункта в другой.
Рассмотрим, например, систему трубопроводов,
по которой перекачиваются нефтепродукты.
Такую систему можно интерпретировать
с помощью связного взвешенного графа,
за вершины которого приняты узловые
пункты системы, а за дуги – трубы между
ними. Каждая труба имеет определенную
пропускную способность, а величина
потока в трубе не может превышать ее
пропускной способности. Пусть нефть
перекачивается из пункта
![]() в пункт
в пункт
![]() .
Естественно потребовать, чтобы при
перекачке не было утечки нефтепродуктов,
т.е. считать, что поток, входящий в любую
вершину, отличную от
.
Естественно потребовать, чтобы при
перекачке не было утечки нефтепродуктов,
т.е. считать, что поток, входящий в любую
вершину, отличную от
![]() и
и
![]() ,
равен потоку, исходящему из нее. Опираясь
на эту интерпретацию, можно ввести
следующие понятия.
,
равен потоку, исходящему из нее. Опираясь
на эту интерпретацию, можно ввести
следующие понятия.
Пусть
![]() – связный орграф. Полюсом
орграфа
– связный орграф. Полюсом
орграфа
![]() называется вершина с нулевой степенью
исхода либо с нулевой степенью захода.
В транспортных системах полюсам
соответствуют начальные и конечные
пункты транспортировки продукта. Поэтому
полюсы с нулевой степенью захода
естественно называть источниками,
а полюсы с нулевой степенью исхода –
стоками.
называется вершина с нулевой степенью
исхода либо с нулевой степенью захода.
В транспортных системах полюсам
соответствуют начальные и конечные
пункты транспортировки продукта. Поэтому
полюсы с нулевой степенью захода
естественно называть источниками,
а полюсы с нулевой степенью исхода –
стоками.
Каждой
дуге
![]() орграфа
орграфа
![]() поставим в соответствие определенный
вес
поставим в соответствие определенный
вес
![]() ),
т.е. положительное число, которое будем
называть пропускной
способностью этой
дуги.
),
т.е. положительное число, которое будем
называть пропускной
способностью этой
дуги.
Полученный
указанным образом взвешенный
ориентированный связный граф с полюсами
назовем сетью
и будем обозначать
![]() .
.
Поскольку
анализ сети более чем с двумя полюсами
легко свести к анализу сети с двумя
полюсами, рассмотрим только двухполюсные
сети, в которых один из полюсов
![]() является источником,
а другой
является источником,
а другой
![]() – стоком.
Для этих вершин
– стоком.
Для этих вершин
![]() ,
,
![]() .
Вершины
.
Вершины
![]() сети, отличные от
сети, отличные от
![]() и
и
![]() ,
будем называть проходными
или внутренними.
,
будем называть проходными
или внутренними.
Потоком
в сети
![]() называется функция
называется функция
![]() ,
удовлетворяющая следующим требованиям
(условия
допустимости потока):
,
удовлетворяющая следующим требованиям
(условия
допустимости потока):
(1)
![]() для каждой дуги
для каждой дуги
![]() (величина
потока через дугу
(величина
потока через дугу
![]() не должна превышать ее пропускную
способность);
не должна превышать ее пропускную
способность);
(2)
![]() для всех вершин
для всех вершин
![]() ,
отличных от источника
,
отличных от источника
![]() и слива
и слива
![]() (закон
сохранения потока).
Здесь
(закон
сохранения потока).
Здесь
![]() – множество всех дуг, входящих в вершину
– множество всех дуг, входящих в вершину
![]() ,
а
,
а
![]() – множество всех дуг, исходящих из нее.
– множество всех дуг, исходящих из нее.
Число
![]() называется величиной
потока,
проходящего через вершину
называется величиной
потока,
проходящего через вершину
![]() .
.
Теорема
3.8.1. Для
любого фиксированного потока
![]()
![]() .
.
Доказательство.
Пусть
![]() – подмножество множества
– подмножество множества
![]() ,
содержащее источник
,
содержащее источник
![]() ,
но не содержащее сток
,
но не содержащее сток
![]() ,
а
,
а
![]() .
Для любой проходной вершины
.
Для любой проходной вершины
![]() согласно закону сохранения потока имеем
согласно закону сохранения потока имеем
![]() .
Поэтому, проведя суммирование по вершинам
множества
.
Поэтому, проведя суммирование по вершинам
множества
![]() ,
получим
,
получим
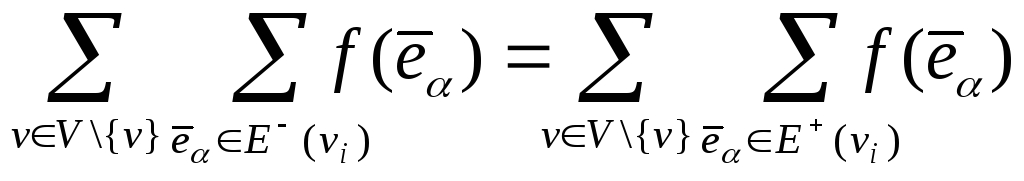
или
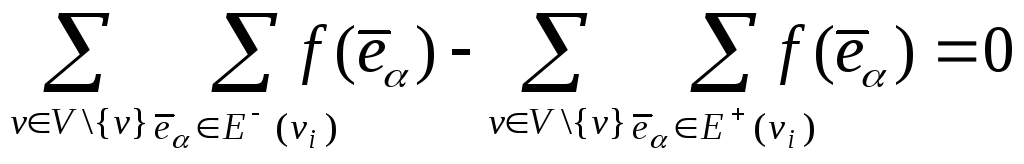 .
.
Включая
в эти суммы поток через вершину
![]() ,
будем иметь
,
будем иметь
![]() .
(3.8.1)
.
(3.8.1)
Множество
всех дуг, у которых начало лежит в
![]() ,
а конец – в
,
а конец – в
![]() ,
обозначим через
,
обозначим через
![]() ,
а множество всех дуг с началом в
,
а множество всех дуг с началом в
![]() и концом в
и концом в
![]() – через
– через
![]() .
Очевидно, что в том случае, когда начальная
и конечная вершины дуги
.
Очевидно, что в том случае, когда начальная
и конечная вершины дуги
![]() лежат в
лежат в
![]() ,
слагаемое
,
слагаемое
![]() входит в обе суммы, стоящие в левой части
равенства (3.8.1). Если в этой разности
привести подобные члены, такие слагаемые
взаимно уничтожатся, т.е.
входит в обе суммы, стоящие в левой части
равенства (3.8.1). Если в этой разности
привести подобные члены, такие слагаемые
взаимно уничтожатся, т.е.
![]() .
.
Таким образом,
![]() .
.
Возьмем
в качестве множества
![]() множество
множество
![]() ,
тогда
,
тогда
![]() ,
а
,
а
![]() – поток, вливающийся в
– поток, вливающийся в
![]() .
Так как для потока, вытекающего из
.
Так как для потока, вытекающего из
![]() ,
имеем
,
имеем
![]() ,
то
,
то
![]() ,
,
и, значит,
![]() .
.
Итак,
![]() .
■
.
■
Величину
![]() называют величиной
потока
называют величиной
потока
![]() ,
будем обозначать ее
,
будем обозначать ее
![]() .
.
Следствие.
Пусть
![]() – подмножество
множества
– подмножество
множества
![]() ,
содержащее источник
,
содержащее источник
![]() ,
но не содержащее сток
,
но не содержащее сток
![]() ,
а
,
а
![]() .
Тогда
.
Тогда
![]() .
.
С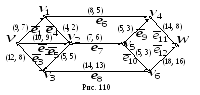 етью
является ориентированный взвешенный
граф на рис. 110. Первый элемент упорядоченной
пары чисел, стоящей над каждой дугой,
обозначает пропускную способность
дуги, а второй – поток через нее. Например,
для вершины
етью
является ориентированный взвешенный
граф на рис. 110. Первый элемент упорядоченной
пары чисел, стоящей над каждой дугой,
обозначает пропускную способность
дуги, а второй – поток через нее. Например,
для вершины
![]() имеем:
имеем:
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
Значит,
величина потока
![]() через вершину
через вершину
![]() равна 11. Так как
равна 11. Так как
![]() ,
,
![]() ,
,
то
величина самого потока
![]() равна 24.
равна 24.
Поток
![]() в сети
в сети
![]() называется максимальным,
если
называется максимальным,
если
![]() для любого допустимого потока
для любого допустимого потока
![]() в этой сети.
в этой сети.
Чтобы
найти поток
![]() в сети
в сети
![]() ,
который при заданных значениях пропускных
способностей дуг имеет максимальную
величину, введем понятие сечения сети.
,
который при заданных значениях пропускных
способностей дуг имеет максимальную
величину, введем понятие сечения сети.
Сечением
![]() сети
сети
![]() называется множество дуг, при удалении
которых сеть становится несвязной,
причем полюсы попадают в разные компоненты
связности.
называется множество дуг, при удалении
которых сеть становится несвязной,
причем полюсы попадают в разные компоненты
связности.
Очевидно,
что каждый путь, выходящий из источника
![]() и входящий в слив
и входящий в слив
![]() ,
проходит хотя бы через одну дугу сечения.
,
проходит хотя бы через одну дугу сечения.
Сечение называется простым, если при удалении любой его дуги оно перестает быть сечением.
Для
сети на рис. 110 простым сечением будет,
например, сечение
![]() .
.
В
симметризации
![]() орграфа
орграфа
![]() с множеством вершин
с множеством вершин
![]() и множеством дуг
и множеством дуг
![]() ,
которая, очевидно, будет связным графом,
дуге
,
которая, очевидно, будет связным графом,
дуге
![]() соответствует ребро
соответствует ребро
![]() ,
а простому сечению – простой разрез.
,
а простому сечению – простой разрез.
Пусть
![]() – множество вершин той компоненты
связности, в которой лежит источник
– множество вершин той компоненты
связности, в которой лежит источник
![]() ,
тогда
,
тогда
![]() ,
и
,
и
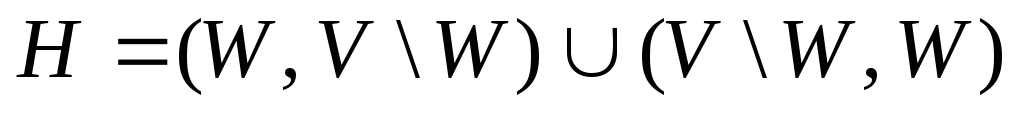 .
.
Если
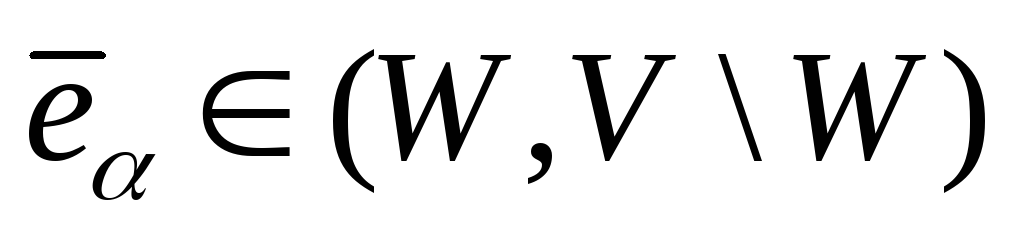 ,
т.е. направление дуги
,
т.е. направление дуги
![]() совпадает с направлением потока, то
соответствующее ей ребро
совпадает с направлением потока, то
соответствующее ей ребро
![]() назовем прямым.
Если дуга
назовем прямым.
Если дуга
![]() ,
соответствующее ей ребро
,
соответствующее ей ребро
![]() назовем обратным.
назовем обратным.
Как было доказано, любой простой разрез разбивает граф ровно на две компоненты связности. Аналогичная теорема имеет место и для простых сечений.
Теорема
3.8.2. Если
в сети
![]() удалить все дуги простого сечения
удалить все дуги простого сечения
![]() ,
то сеть распадется ровно на две компоненты
связности, одна из которых содержит
источник
,
то сеть распадется ровно на две компоненты
связности, одна из которых содержит
источник
![]() ,
а вторая – сток
,
а вторая – сток
![]() .
.
Введем для простого сечения понятия пропускной способности и величины потока.
Пропускной
способностью простого сечения
![]() называется число
называется число
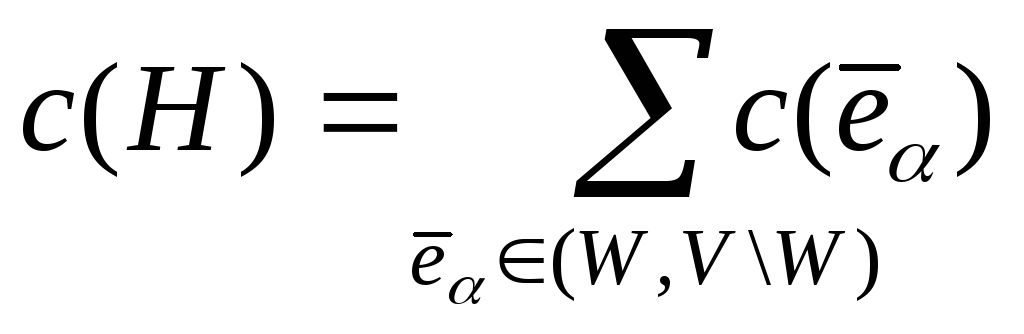 .
.
Величиной
потока
![]() в простом сечении
в простом сечении
![]() называется разность
называется разность
 .
.
Простое
сечение
![]() (рис. 110) имеет пропускную способность
(рис. 110) имеет пропускную способность
![]() ,
,
а величина потока через это сечение
![]() .
.
Величина
потока через сечение
![]() ,
дуга
,
дуга
![]() которого имеет направление, противоположное
направлению потока, вычисляется так:
которого имеет направление, противоположное
направлению потока, вычисляется так:
![]() .
.
Простое
сечение
![]() сети
сети
![]() называется минимальным,
если его пропускная способность не
больше пропускной способности любого
другого сечения
называется минимальным,
если его пропускная способность не
больше пропускной способности любого
другого сечения
![]() этой сети:
этой сети:
![]() .
.
Теорема
3.8.3. Пусть
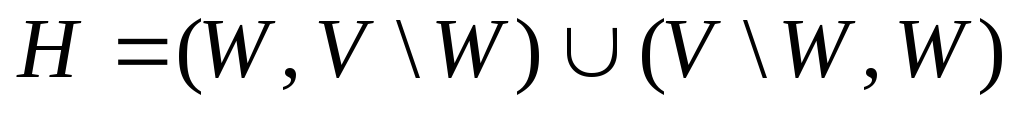 – простое сечение сети
– простое сечение сети
![]() ,
где
,
где
![]() – подмножество множества
– подмножество множества
![]() ,
содержащее
,
содержащее
![]() ,
но не содержащее
,
но не содержащее
![]() .
Тогда
.
Тогда
![]()
для
любого потока
![]() .
.
Доказательство. Имеем
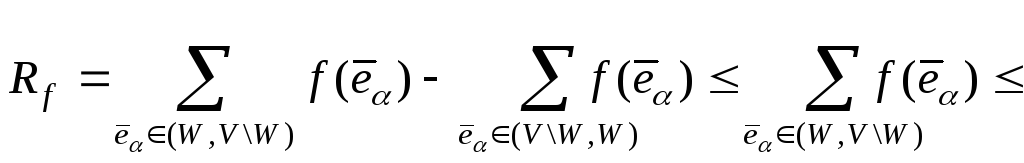
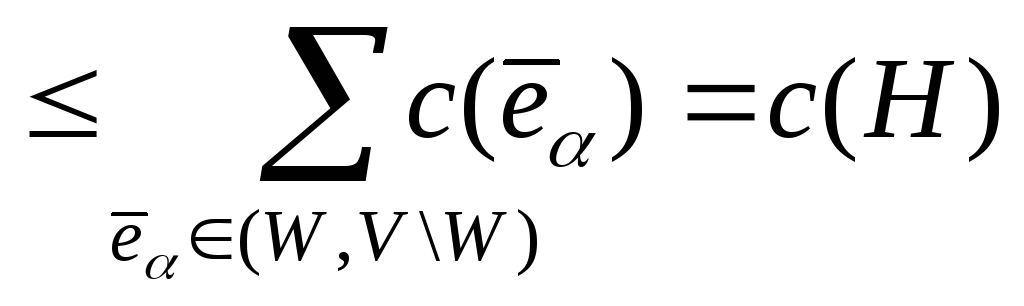 .
■
.
■
Следствие
1. Для
некоторого потока
![]() и простого сечения
и простого сечения
![]() сети
сети
![]() равенство
равенство
![]() имеет место тогда и только тогда, когда
имеет место тогда и только тогда, когда
![]() для всех
для всех
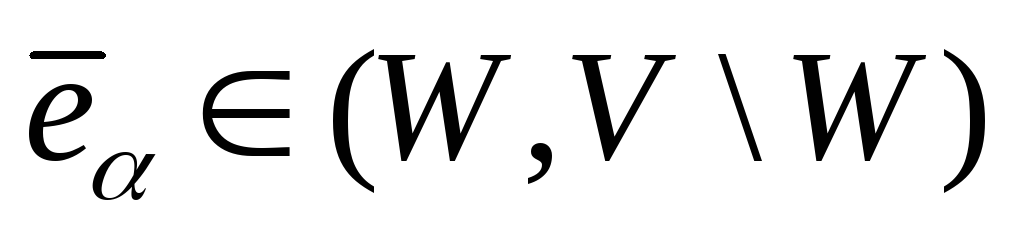 и
и
![]() для всех
для всех
![]() .
.
Следствие
2. Если
для некоторого потока
![]() имеет место равенство
имеет место равенство
![]() ,
то
,
то
![]() – максимальный поток, а
– максимальный поток, а
![]() – минимальное сечение.
– минимальное сечение.
Докажем, что в любой сети можно создать поток максимальной величины.
Теорема
3.9.4
(Форд–Фалкерсон).
Максимальный
поток
![]() в сети
в сети
![]() такой, что
такой, что
![]() ,
,
существует.
Доказательство. Приведем конструктивное доказательство сформулированной теоремы. Это позволит сразу указать алгоритм построения минимального сечения и определения соответствующего максимального потока.
Пусть
в сети
![]() с источником
с источником
![]() и стоком
и стоком
![]() задан некоторый допустимый поток
задан некоторый допустимый поток
![]() .
Построим с помощью него простое сечение
.
Построим с помощью него простое сечение
![]() сети, используя следующие процедуры.
сети, используя следующие процедуры.
Шаг
1. Положим
![]() .
.
Шаг
2. Если в
![]() существует вершина
существует вершина
![]()
![]() такая, что
такая, что
![]() или
или
![]() для некоторой вершины
для некоторой вершины
![]()
![]() ,
то включить
,
то включить
![]() в
в
![]() .
Повторять шаг 2 до тех пор, пока это
возможно.
.
Повторять шаг 2 до тех пор, пока это
возможно.
В
результате придем к одному из следующих
случаев:
1)
![]() ,
2)
,
2)
![]() .
Рассмотрим эти случаи.
.
Рассмотрим эти случаи.
Случай
1. Если
![]() ,
то в соответствии с шагом 2 для всех дуг
,
то в соответствии с шагом 2 для всех дуг
![]() будет иметь место равенство
будет иметь место равенство
![]() ,
а для всех дуг
,
а для всех дуг
![]() выполняться равенство
выполняться равенство
![]() .
Поэтому в силу следствия 1 предыдущей
теоремы поток
.
Поэтому в силу следствия 1 предыдущей
теоремы поток
![]() будет максимальным, а построенное
сечение
будет максимальным, а построенное
сечение
![]() – минимальным.
– минимальным.
Случай
2. Если
![]() ,
то в симметризации
,
то в симметризации
![]() ,
полученной в результате стирания
ориентации дуг орграфа
,
полученной в результате стирания
ориентации дуг орграфа
![]() ,
существует цепь, соединяющая
,
существует цепь, соединяющая
![]() с
с
![]() и удовлетворяющая свойствам:
и удовлетворяющая свойствам:
![]() для
каждого прямого ребра
для
каждого прямого ребра
![]() ,
,
![]() для
каждого обратного ребра
для
каждого обратного ребра
![]() .
.
Такую
(![]() )-цепь
называют аугментальной
(увеличивающей).
)-цепь
называют аугментальной
(увеличивающей).
Для прямых ребер аугментальной цепи вычислим величину
![]() ,
,
а для обратных ребер – величину
![]() .
.
Найдем
![]() .
Прибавим
.
Прибавим
![]() к значениям потока на всех прямых ребрах
аугментальной цепи, и вычтем
к значениям потока на всех прямых ребрах
аугментальной цепи, и вычтем
![]() из значений потока на всех обратных
ребрах. В результате получим новый
допустимый поток
из значений потока на всех обратных
ребрах. В результате получим новый
допустимый поток
![]() ,
величина которого на
,
величина которого на
![]() больше, чем величина исходного потока
больше, чем величина исходного потока
![]() .
.
С
помощью шагов 1, 2 аналогичным образом
для потока
![]() найдем новое сечение сети и произведем
следующее увеличение величины потока
в сети и т.д. Поскольку пропускные
способности дуг – конечные величины,
а общая величина потока увеличивается,
наступит момент, когда дальнейшее
наращивание потока станет невозможным,
т.е.
найдем новое сечение сети и произведем
следующее увеличение величины потока
в сети и т.д. Поскольку пропускные
способности дуг – конечные величины,
а общая величина потока увеличивается,
наступит момент, когда дальнейшее
наращивание потока станет невозможным,
т.е.
![]() .
А это означает, что будет найден
максимальный поток и построено
соответствующее ему минимальное сечение.
■
.
А это означает, что будет найден
максимальный поток и построено
соответствующее ему минимальное сечение.
■
Следствие 1. Если величина потока в сети равна сумме пропускных способностей дуг, выходящих из источника, то этот поток является максимальным.
Следствие 2. Если величина потока в сети равна сумме пропускных способностей дуг, входящих в сток, то этот поток максимальный.
Вытекающий из приведенного доказательства алгоритм поиска максимального потока в сети и соответствующего ему минимального сечения (в той или иной его модификации) называют алгоритмом Форда–Фалкерсона.
В
основе названного алгоритма лежит
последовательное увеличение потока в
сети с помощью построения аугментальных
цепей от
![]() к
к
![]() .
Алгоритм «запускают» с произвольного
допустимого потока (обычно, нулевого).
Вершинам орграфа
.
Алгоритм «запускают» с произвольного
допустимого потока (обычно, нулевого).
Вершинам орграфа
![]() присваиваются метки, показывающие,
вдоль каких дуг и на сколько может быть
увеличен поток. Затем выбирают некоторую
аугментальную цепь, поток через дуги
этой цепи увеличивают до максимально
допустимой величины, а после этого все
метки в вершинах стирают. Вновь полученный
поток выбирается в качестве исходного
для следующего шага. Процесс продолжается
до тех пор, пока такие потоки можно
построить.
присваиваются метки, показывающие,
вдоль каких дуг и на сколько может быть
увеличен поток. Затем выбирают некоторую
аугментальную цепь, поток через дуги
этой цепи увеличивают до максимально
допустимой величины, а после этого все
метки в вершинах стирают. Вновь полученный
поток выбирается в качестве исходного
для следующего шага. Процесс продолжается
до тех пор, пока такие потоки можно
построить.
Уточним,
как помечаются вершины. Пусть
![]() – вершина сети. Если поток вдоль дуги
– вершина сети. Если поток вдоль дуги
![]() может быть увеличен, то вершине
может быть увеличен, то вершине
![]() припишем метку
припишем метку
![]() ,
если же поток может быть уменьшен, –
метку
,
если же поток может быть уменьшен, –
метку
![]() ;
;
![]() – величина дополнительного потока,
который может проходить от
– величина дополнительного потока,
который может проходить от
![]() к
к
![]() .
.
Рассмотрим действие алгоритма на конкретном примере.
Задача 8.1. Найти максимальный поток и соответствующее ему минимальное сечение для сети на рис. 110.
Решение.
1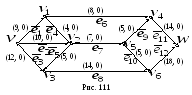 .
Возьмем нулевой поток в качестве
исходного (рис. 111); вершине
.
Возьмем нулевой поток в качестве
исходного (рис. 111); вершине
![]() присвоим метку
присвоим метку
![]() .
.
2.
Присвоим метки вершинам
![]() ,
,
![]() и
и
![]() ,
смежным с вершиной
,
смежным с вершиной
![]() .
Вершина
.
Вершина
![]() при этом получит метку
при этом получит метку
![]() ,
вершина
,
вершина
![]() – метку
– метку
![]() ,
а вершина
,
а вершина
![]() – метку
– метку
![]() .
.
