DM_Mnozhestva (1)

ЧАСТЬ I. МНОЖЕСТВА, СООТВЕТСТВИЯ, ОТНОШЕНИЯ
1. Операции над множествами
Запись x A означает, что элемент x принадлежит множеству A . Если x		не является эле-
ментом множества А , то пишут x A. Два множества A и	B считаются равными,	если они состоят
из одних и тех же элементов. Будем писать А В , если А и	В равны и А В в противном случае.
Множество называется пустым и обозначается , если оно не содержит элементов.
Будем говорить, множество А включено во множество В , и писать А В , если каждый эле-
мент множества А является элементом множества В . В этом случае А называется		подмножеством
множества В . Считается, что для любого А справедливо включение А.

Если А В и А В , то будем писать А В и говорить, что множество А строго включено во множество В или множество А является собственным подмножеством множества В .

Семейство всех подмножеств данного множества А обозначается P A .

Мощностью конечного множества А будем называть число его элементов. Мощность множества (не обязательно конечного) А обозначается А .

Объединением множеств А и В называется множество

А В х х А или х В .

Пересечением множеств А и В называется множество

А В х х А и х В .

Разностью множеств А и В называется множество

А \ В х х А и х В .

Если все рассматриваемые множества являются подмножествами некоторого универсального множества U , то разность U \ A называется дополнением А и обозначается A .

Симметрической разностью множества А и В называется множество А В А \ В В \ А .

Будем говорить, что множества А и В находятся в общем положении, если существуют такие элементы a, b, c , что a A и a B , b B и b A, c A и c B , иначе говоря, эти множества не являются подмножествами друг друга и пересекаются.

Задание 1.1. Для универсального множества U 5, 4, 3, 2, 1,1, 2,3, 4, 5 , множества А , за-

данного списком, и для В , являющегося множеством корней уравнения x4 x3 x2 x 0. 1. Найти множества: A B , B A, A \ B , B \ A , A B , B , C A B A .

1

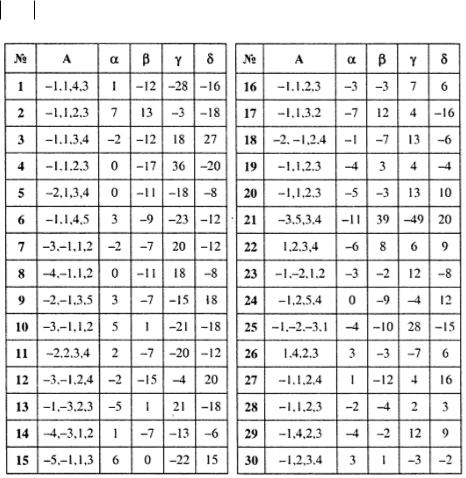
2. Выяснить, какая из пяти возможностей выполнена для множества А и С : А C , или C A , или

АС , или А С , или А и C находятся в общем положении.

3.Найти P B и P B .

Пример решения задания 1.1.

Решим задание 1.2 для А 1, 2, 3, 4 и уравнения x4 7x3 6x2 32x 32 0 .

Решение. Сначала найдём множество B корней данного уравнения. Подбором устанавливаем,

что корнем исходного многочлена	x4 7x3 6x2 32x 32 является 1; поделив этот многочлен на
х 1, получим многочлен x3 6x2	32 . Также подбором устанавливаем, что 2	является корнем
многочлена x3 6x2 32 и делим	этот многочлен на x 2 . Получим многочлен	x2 8x 16 . Его

корни совпадают и равны 4.
Итак, множество B найдено,			B 2, 1,	4 . Теперь решаем пункты 1-3 данного задания.
1. A B 4, 2,1,3,4 , B A 2, 1 ,				A \ B 4, 3 , B \ A 4 , A B 4, 3, 4 ,
		5, 4, 3, 1,2,3,5 , C A B A 4, 3, 4 1, 2, 3, 4 4 1, 2 2,1,4 .
	B
2. Так как 4 A и 4 C ,			4 C и 4 A , 1 A C , то множества А и C находятся в об-
щем положении.

2

3. P B , 2 , 1 , 4 , 2,1 , 2, 4 , 1, 4 , 2, 1, 4 . Видим, что P B содержит 8 эле-

ментов, т.е. P B 8 .

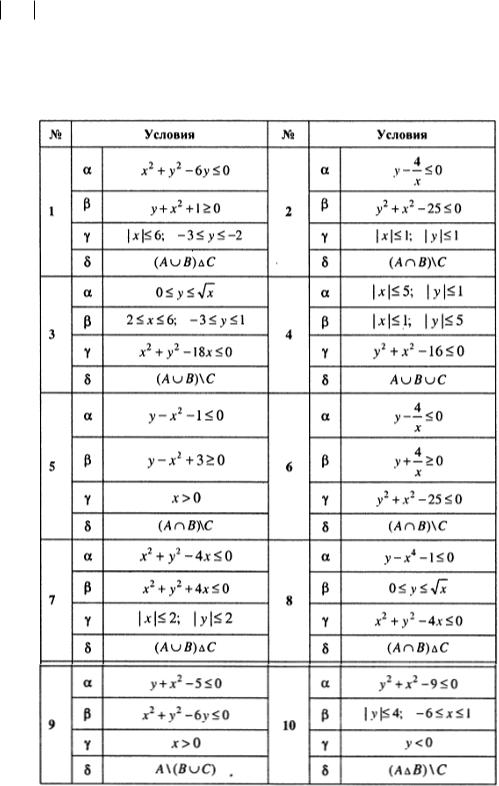
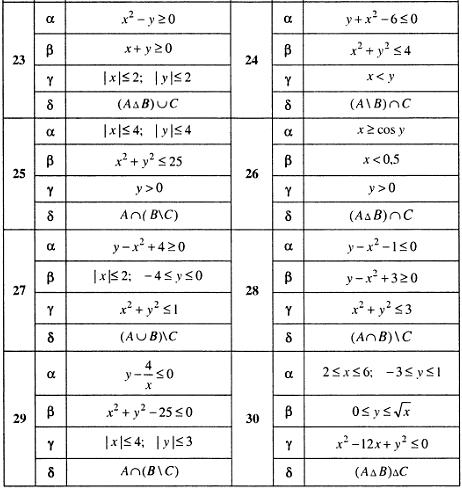
Задание 1.2. Пусть A, B и С – множество точек плоскости, координаты которых удовлетворяют условиям α, β и γ соответственно. Изобразите в системе координат x0 y множество D , полученное из множества A, B и C по формуле δ .

3

4

Пример решения задания 1.2.

Пусть A, B и С множество точек плоскости, координаты которых удовлетворяют условиям

x 2 y , x2 y2 4 и		x		2;		y		2 соответственно. Изобразите в системе координат xOy множе-
ство D , полученное из множеств A, B и C по формуле A \ B C .
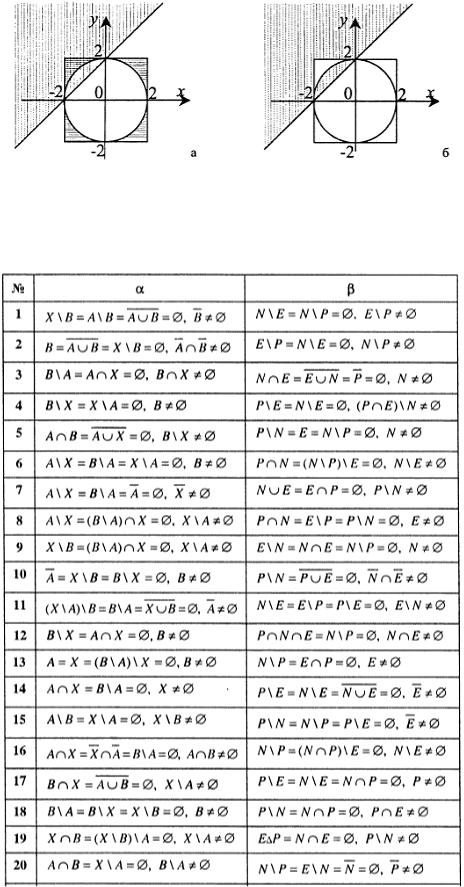
Решение. Множество B представляет из себя множество точек круга радиуса 2 с центом в
начале координат, включающего границу, А множество точек плоскости, расположенных выше и на

прямой y x 2 , и C множество точек, лежащих внутри и на границе квадрата			x		2 ;		y		2 .
Отметим горизонтальной штриховкой множество B C , а	вертикальной		–		множество A
(рис.1, а)
Удалив из области, помеченной вертикальной штриховкой, точки области, помеченной гори-
зонтальной штриховкой, мы получим множество точек, образующих	D . Изобразим результат, отме-
тив точки множества D вертикальной штриховкой (рис. 1, б).

5

	Рис. 1
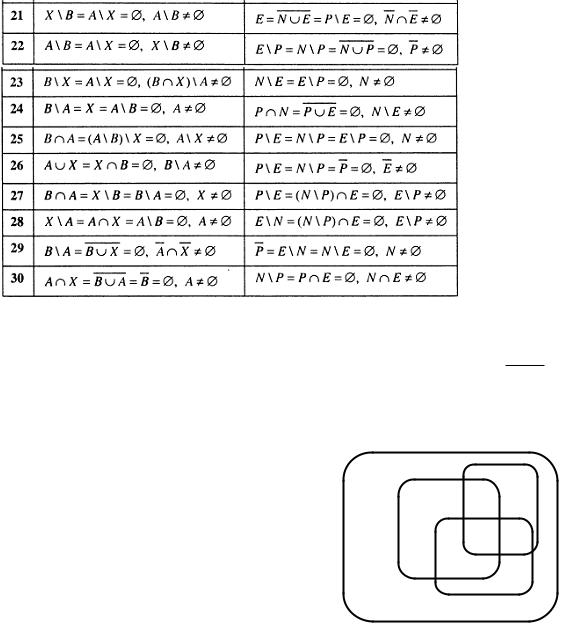
Задание 1.3.
1.	Существуют ли множества А, В, Х такие, что выполняется набор условий α ?
2.	Существуют ли множества N, E, P такие, что выполняется набор условий β ?

6

Пример решения задания 1.3.

1. Существуют ли множества А, В, Х такие, что выполняется набор условий: А В ,

X A , В \ А ?

Решение. Изобразим множества А, В, Х в виде прямоугольников, расположенных на плоскости в общем положении, и поставим в каждой области, на которые плоскость разбита прямоугольниками, по одному символу: символ 4, например, обозначает список всех элементов, попавших во множества А и В , но не попавших в Х и т.д. Теперь составим множества А, В, Х и универсальное множество U (рис.2):

U 1, 2,	3, 4, 5, 6, 7,8 , A 1, 2, 4, 5 ,
B 4, 5,	6, 7 ,	X 2, 3, 5, 7 .

U		В
А	4	6
1	5
		7
	2
8		3 Х

Рис. 2

Изменим множества А, В, Х так, чтобы выполнились условия нашего задания.

			, следует, что множество U \ A B не должно содержать элементов,
Из того, что		А В
т.е. из U удаляем 8	и 3. Чтобы выполнилось условие X A , нужно удалить элементы списков 1,
4, 7. Тогда получится,			что множества А, В, Х и U	имеют следующий вид: A 2,5 X ,
B 5, 6 , U 2, 5, 6 .			Заметим, что для этих множеств	B \ A 6 .

Если под символами 2, 5 и 6 будем понимать соответствующие числа, то мы получим конкретный пример множества А, В, Х , для которых выполнены все условия заданного набора требований.

2. Существуют ли множества N, E, P такие, что выполняется набор условий:

E \ N P \ E , P \ N ?

7

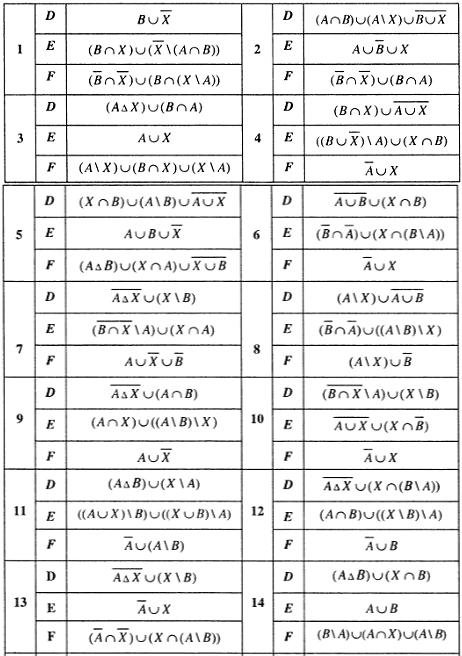
Решение. Попробуем построить множества N, E, P так же, как мы это делали в п. 1. Пусть N 1, 2, 4, 5 , E 4, 5, 6, 7 , P 2, 3, 5, 7 . Чтобы выполнялось условие E \ N , удаляем элементы списков 6, 7. Для выполнения условия P \ E удаляем элементы из списков 2, 3. Но тогда множество P \ N не будет содержать элементов. Итак, мы показали, что этот набор условий противоречив, т.е. не существует множеств N, E, P таких, что выполнены условия упражнения.

Задание 1.4. Выяснить взаимное расположение множеств D, E, F , если А, В, Х – произвольные подмножества универсального множества U .

8

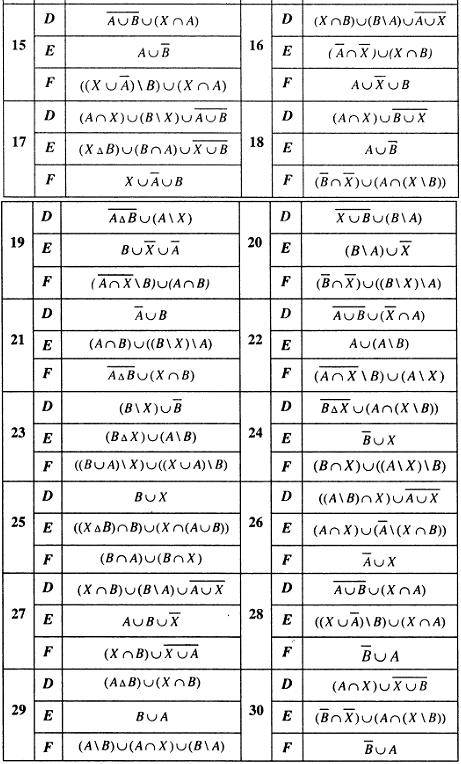
Пример решения задания 1.4.

Выяснить взаимное расположение множеств:

D B \ X A \ B ,	E A \ B \ X ,	F A B , если А, В, Х – произвольные подмножества уни-
версального множества U .
Решение. Возьмём множества		А, В, Х , находящиеся в общем положении: А 1, 2, 4, 5 ,
		9

B 4, 5, 6, 7 ,	X 2, 3, 5, 7 . В нашем случае, как и при решении задания 1.3,				цифры обозначают
соответствующие списки переменных. Тогда В \ Х 4, 6 ,				А \ В 1, 2 ,	A \ B \ X 1, 2, 5 ,
A B 1, 2, 4, 5, 6, 7 , B \ X A \ B 1, 2, 4, 6 , т.е.
	D 1, 2, 4, 6 , E 1, 2, 5 ,		F 1, 2, 4, 5, 6, 7 .
Итак, видим, что включения		D F и E F	выполняются для произвольных множеств
А, В, Х .
Если символы 1, 2, 4, 5, 6, 7		обозначают соответствующие числа, имеем, что 4 D и 4 E ,

5 E и 5 D , 1 D E , т.е. множества D и E могут находиться в общем положении.

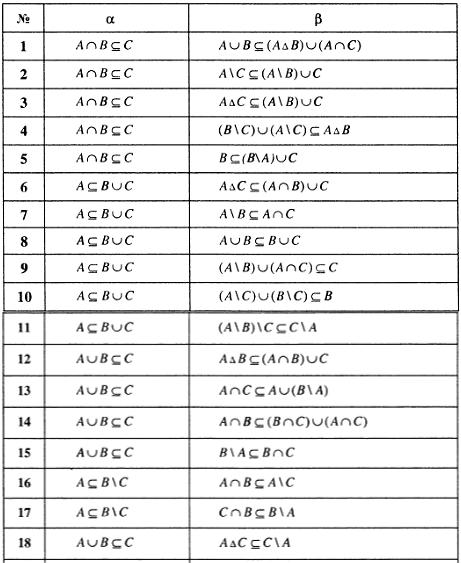
Задание 1.5. Проверить, что для любых множеств А, В, С выполнение включения α влечёт выполнение включения β .

10