Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тольяттинский государственный университет

Предмет:

Теоретические основы электротехники

Файл:

Лекция по электростатике

.pdf

Скачиваний:

Добавлен:

28.05.2015

Размер:

467.81 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

Глава 1. ЭЛЕКТРОСТАТИКА

§ 1. Электрический заряд и его свойства. Закон Кулона.

Все тела в природе способны электризоваться, т.е. приобретать электрический заряд.

Электрический заряд обозначается q. Измеряется в системе единиц СИ в кулонах [q]=Кл.

Электрический заряд частицы является одной из основных, первичных её характеристик. Ему присущи следующие фундаментальные свойства:

1.Электрический заряд существует в 2-х видах: положительный и отрицательный. Заряды одного знака отталкиваются, разных знаков - притягиваются.

2.Электрический заряд квантуется, то есть может принимать только определённые дискретные значения. Заряд всех элементарных частиц одинаков по абсолютной величине (элементарный заряд е=1,6 10-19 Кл) или равен нулю. Всякий заряд q образуется совокупностью элементарных зарядов: q Ne .

3.Электрический заряд является релятивистки инвариантным: его величина не зависит от системы отсчёта, а значит, не зависит от того, движется он или покоится.

4.Суммарный заряд электрически изолированной системы не может изменяться.

Это утверждение носит название закона сохранения электрического заряда.

В учении об электричестве вводится понятие точечного заряда.

Точечным зарядом называется заряженное тело, размерами которого можно пренебречь по сравнению с расстоянием от этого тела до других заряженных тел.

В электричестве понятие точечного заряда играет такую же роль, как материальная точка в механике.

Закон, которому подчиняется сила взаимодействия точечных зарядов, был установлен в 1785 г. Кулоном.

Закон Кулона: Сила взаимодействия двух неподвижных точечных зарядов пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между ними:

F k

r 2

где k

– коэффициент пропорциональности,

системе

единиц СИ:

=9 109 м/Ф,

8,85 10 12 Ф/м - электрическая постоянная.

В векторном виде закон Кулона:

где

- единичный

r 2

вектор.

Кулоновская сила направлена по прямой, соединяющей взаимодействующие заряды:

§ 2. Электрическое поле. Напряженность поля.

Взаимодействие между зарядами осуществляется через поле. Любой заряд изменяет свойства окружающего его пространства - создает в нем электрическое поле. Это поле проявляет себя в том, что помещенный в какую-либо его точку другой заряд испытывает действие силы.

Электрическое поле - вид материи, посредством которого осуществляется взаимодействие между электрическими зарядами.

Электростатическое поле - поле, созданное неподвижными зарядами. Исследуем поле, создаваемое неподвижным точечным зарядом q, с помощью

точечного пробного заряда qпр. Поместим qпр на расстоянии r от q. По закону Кулона на qпр действует сила:

				q


F	qпр


		k			2	.
			r

	На разные пробные заряды будут действовать разные силы: q'пр -
	... Но отношение		будет одним и тем же, и зависит лишь от q и
F		F / qпр

это отношение можно взять за характеристику поля:

E .

qпр

F ; q"пр - r. Значит,

Напряженность – есть векторная физическая величина, численно равная силе, действующей на единичный точечный заряд, находящийся в данной точке поля. Напряженность является силовой характеристикой электрического поля.

Направление вектора напряженности совпадает с направлением силы. Единица напряженности в системе СИ [E]=B/м.

Вектор напряженности направлен радиально от точечного заряда, если он положительный и радиально к заряду, если он отрицательный:

Для поля точечного заряда, как следует из предыдущих формул, модуль вектора напряженности находится по формуле:

EТЗ	1	q	k	q	.

	4 0 r 2		r 2
	4 0 r 2		r 2
	2

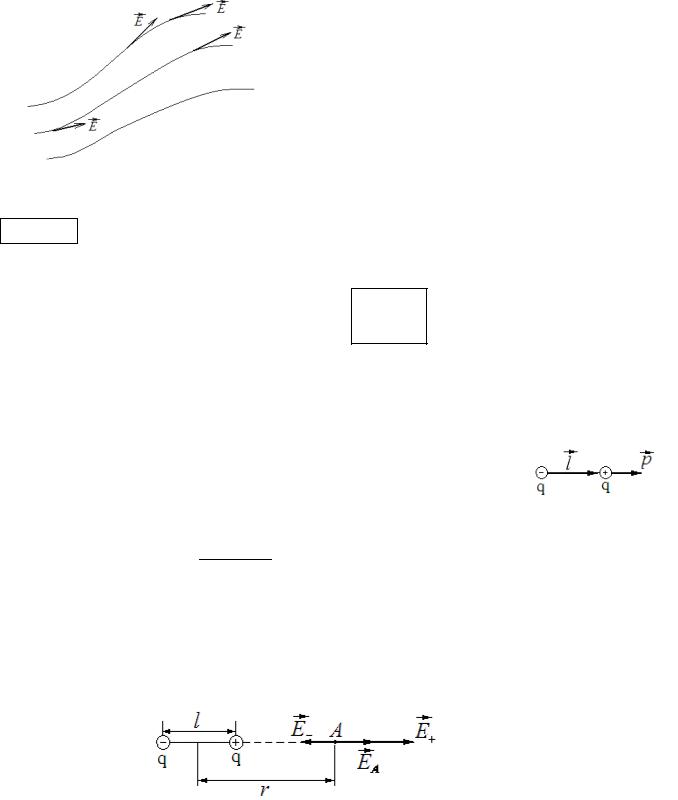
Графически электростатические поля изображают при помощи силовых

линий (линий напряженности E ).

Силовой линией называется воображаемая линия, касательные к которой в каждой точке

совпадают с вектором напряженности E . Силовые линии электростатического поля нигде кроме заряда не начинаются и не заканчиваются. Густота силовых линий характеризует числовое значение напряженности.

Электростатическое поле называется однородным, если вектор

напряженности в любой точке пространства постоянен по величине и направлению

E const .

Принцип суперпозиции (наложения) полей: напряженность поля системы зарядов равна векторной сумме напряженностей полей, которые создавал бы

каждый из зарядов системы в отдельности: E Ei .

§ 3. Электрический диполь.

Электрический диполь - система двух равных по модулю разноименных точечных зарядов (+q, -q), расстояние l, между которыми значительно меньше расстояния до рассматриваемых точек поля.

Вектор, направленный по оси диполя от отрицательного заряда к положительному и равный расстоянию между ними,

называется плечом диполя l .

Вектор, совпадающий по направлению с плечом диполя и равный произведению заряда q на плечо, называется электрическим моментом диполя или

дипольным моментом:

Электростатическое поле диполя можно рассчитать, применив принцип

суперпозиции,

согласно

которому напряженность поля диполя в

произвольной

точке:

E E E ,

где

E , E

- напряженности полей,

создаваемых

соответственно положительным и отрицательным зарядами.

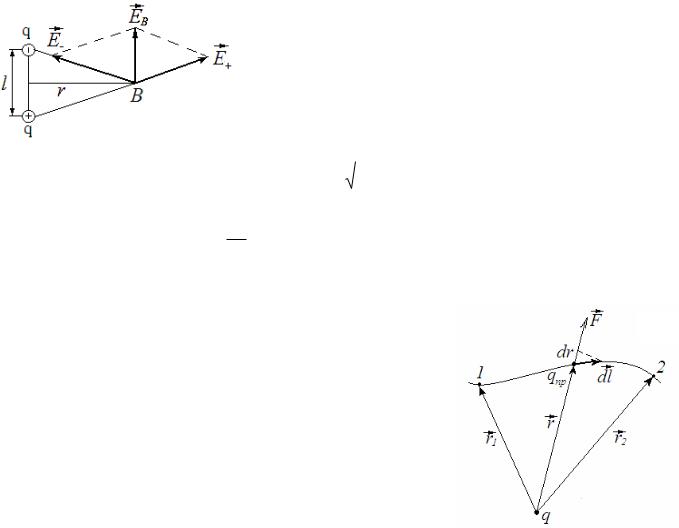
3.1. Расчет напряженности поля на продолжение оси диполя.


По принципу суперпозиции:	EA E E . Из рисунка видно, что модуль

результирующей напряженности:				EA E E .
Обозначим расстояние от точки А до середины плеча за r, тогда:
E	1	q	,	E	1	q	,

	4 0	r l / 2 2			4 0	r l / 2 2

r l / 2

E A

r l / 2

l / 2 2

4 0

r l / 2 2 r l / 2 2

0 r l / 2 2

Из определения диполя:

r , тогда:

q r 2

rl l 2 / 4 r 2 rl l 2 / 4

q 2l

1 2 p

4 0

r l / 4 2

4 0 r 3

3.2. Расчет напряженности поля на перпендикуляре, восстановленном к оси диполя из его середины.

Подставим значение Е+:

	EB	1 q

		4 0 r 2

Обозначим за r - -расстояние от точки В до середины плеча диполя. Точка В равноудалена от зарядов,

поэтому: E E

4 0 r 2 l / 2 2

4 0 r 2

Из

подобия

равнобедренных

треугольников

( q q B, BEB E ) получим:

, откуда

EB E

r 2 l / 2 2

4 0 r 3

§ 4. Потенциал

Рассмотрим поле неподвижного заряда q. Будем перемещать в этом поле точечный заряд qпр из точки 1 в точку 2 вдоль произвольной траектории. При этом

будет совершаться работа.

При перемещении заряда qпр												на dl			совершается
										Fdl cos Fdr .
элементарная работа:						dA Fdl				Fdl cos Fdr .
Из рисунка dr dl cos .
Работа при перемещении из точки 1 в точку 2:
2	2 qqпр			dr			qqпр		r2 dr			1		qqпр		qqпр
A12 Fdr
		4				4						4
		4	0	r	2	4				r	2	4	0		r	r
1	1		0	r				0 r		r			0		1	2
									1

Отсюда видно, что работа не зависит от траектории движения заряда qпр, а определяется только начальным и конечным положением. Следовательно,

электростатическое поле - потенциально, а электростатические силы - консервативны.

Работа консервативных сил равна убыли потенциальной энергии:

A12 Wп Wп1 Wп2 .

Это приводит к выражению потенциальной энергии заряда qпр:

W	1	qqпр	.
W			.
п	4 0	r
	4 0	r

Разные заряды обладают в одной и той же точке поля разной потенциальной

энергией: q	пр	W , q		W		, … Однако отношение W / q	пр	одно и то же.
	пр	п	пр		п	п	пр
Таким образом, вводится еще одна характеристика ЭСП, которая получила
название потенциал:				Wп	.
название потенциал:				qпр	.
				qпр

Потенциал – есть скалярная физическая величина, численно равная потенциальной энергии, которой обладал бы в данной точке поля единичный положительный заряд. Потенциал является энергетической характеристикой электростатического поля.

В системе единиц СИ потенциал измеряется в вольтах [φ]=В.

Тогда выражение для потенциальной энергии и работу можно записать через

потенциал:		Wп q		.
	A12 Wп Wп1 Wп2 q 1 q 2 q( 1 2 )							.
Потенциал поля точечного заряда:			ТЗ		1	q	.
Потенциал поля точечного заряда:			ТЗ		4 0	r	.
					4 0	r

§ 5. Циркуляция вектора напряженности ЭСП

Вернемся к работе по перемещению заряда в электростатическом поле. Если будем перемещать заряд по замкнутой траектории, то А=0. Это можно выразить

через замкнутый интеграл:

	A dA Fdl			qEdl	q Edl 0
		l	l	l	l

Так как заряд q не равен нулю, то нулю равен интеграл: Edl =0.
						l

Интеграл вида: Edl		- называется циркуляцией вектора напряженности E .
	l

Тогда: Edl	Edl cos El dl 0 .
l	l		l

Для ЭСП циркуляция вектора напряженности E						вдоль произвольной

замкнутой траектории равна нулю.

Отсюда следует, что линии напряженности ЭСП не могут быть замкнутыми.

§ 6. Связь напряженности E с потенциалом φ

Одну и ту же точку электростатического поля мы можем охарактеризовать либо напряженностью, либо потенциалом. Значит, между ними должна существовать связь.

Чтобы найти эту связь, воспользуемся выражением работы. Рассмотрим только ось X. Пусть заряд q переместился параллельно оси X, вследствие чего его координата x получила приращение dx. При этом силы поля совершат работу:

2	2		2	2
A12 dA		Fdl	qEdl	qEx dx .
1	1		1	1

С другой стороны эта работа должна быть равна убыли потенциальной энергии:

1 2

A12 Wп Wп1 Wп2 q( 1 2 ) qd qd .

2 1

Приравняем эти выражения. Равенство интегралов обуславливает равенство

их подынтегральных выражений: Exdx d . Из этого следует: Ex .

Производная по x, вычисленная при условии, что координаты у и z остаются постоянными, называется частной производной.

Аналогично можно записать выражения для компонент напряженности по

осям у и z: E y , Ez .

y z

Представим вектор напряженности E через его компоненты:

grad

E E

Вектор с компонентами		,		,		, где φ - скалярная функция координат
Вектор с компонентами		,		,		, где φ - скалярная функция координат
	x		y
	x		y		z

x, y, z, называется градиентом функции φ.

Градиент функции можно представить с помощью оператора Гамильтона или оператора набла.


		i			j			k	- оператор Гамильтона или оператор набла.

	x		y				z
						grad

Таким образом				E						.

Напряженность поля равна градиенту потенциала со знаком «-». Знак минуса

показывает, что вектор E							направлен в сторону убывания потенциала.
Выберем произвольное									направление l. По аналогии можно записать:

El - проекция вектора напряженности на произвольное направление l равна

взятой с обратным знаком производной φ по l, т.е. скорости убывания потенциала при перемещении вдоль направления l.

Эквипотенциальной поверхностью называется воображаемая поверхность, все точки которой имеют одинаковый потенциал.

Уравнение эквипотенциальной поверхности: φ(x, y, z)=const.

Для	эквипотенциальной поверхности		справедливо			утверждение: вектор

напряженности E перпендикулярен эквипотенциальной поверхности. Докажем это.
При перемещении по		эквипотенциальной	поверхности			на dl потенциал не
изменится,	т.е. d 0 . Согласно равенства:		El		проекция Еl=0. Из этого
изменится,	т.е. d 0 . Согласно равенства:		El	l	проекция Еl=0. Из этого
				l

следует, что сам вектор		E перпендикулярен эквипотенциальной поверхности.

§ 7. Поток вектора напряженности. Теорема Гаусса.

Густота силовых линий характеризует числовое значение напряженности. Условились, что число силовых линий, пронизывающих единицу

поверхности, перпендикулярной линиям

вектора E , должно быть равно модулю вектора напряженности.

Тогда число линий напряженности, пронизывающих элементарную площадку

dS, нормаль которой n образует угол α c

вектором E равно:

EdS EdS cos En dS dФE .

Величина dФE называется потоком вектора напряженности через площадку dS.

En - проекция вектора	E на нормаль к площадке dS.
Для произвольной поверхности S поток вектора напряженности находится
через интеграл:
		ФE dФ
		ФE dФ	EdS .
		S
Для произвольной замкнутой поверхности S поток вектора напряженности
находится через замкнутый интеграл:

		ФE dФ EdS	En dS .
		S	S
Поток вектора		зависит от выбора направления нормали
Поток вектора	E	зависит от выбора направления нормали		n . За

положительное направление нормали принимается внешняя нормаль, т.е. нормаль,

направленная наружу области, охватываемой поверхностью.
Понятие	потока	вектора			напряженности
используется в теореме Гаусса (немецкий ученый), которая
применяется для	расчета напряженности				поля			системы

зарядов. Эта теорема определяет поток вектора								E через
произвольную замкнутую поверхность.
Рассмотрим	точечный		заряд		q.			Выберем
произвольную замкнутую поверхность в виде сферы
радиуса r, чтобы заряд находился в центре этой сферы.
	En dS	q		4 r 2		q
Поток вектора напряженности E равен: ФE							.

	S	4 0 r 2				0

Эта формула справедлива для произвольной замкнутой поверхности любой формы. Выберем произвольную форму замкнутой поверхности, с зарядом q внутри.

Возьмем одну из линий напряженности. Она то входит, то выходит из поверхности.

Поток считается	положительным, если	линия		выходит из	поверхности, и
			E

отрицательным - если линия E входит в поверхность. Нечетное число пересечений
при вычислении	потока сводится к	одному	пересечению.		Если замкнутая

поверхность

не

охватывает заряд,

то

поток

сквозь

нее

равен

нулю, т.к. число линий

входящих в поверхность равно числу

линий выходящих из нее.

Рассмотрим

произвольную

поверхность,

окружающую

электрических зарядов.

По принципу суперпозиции:

E Ei ,

тогда: Ф

EdS

S i1

i1 S

i1 0

Теорема Гаусса: Поток вектора напряженности ЭСП в вакууме через произвольную замкнутую поверхность равен

алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на электрическую постоянную:

	1	N
ФE		qi	.
	0
		i1

Вобщем случае, когда заряды размазаны с некоторой объемной плотностью

dVdq , то суммарный заряд: qi dV . Тогда теорема Гаусса запишется:

	V	En dS	1 dV .
ФE EdS		En dS	1 dV .

S		S	0 V

Для тел, имеющих протяженные размеры, используются понятия:

dVdq - объемная плотность заряда – заряд, приходящийся на единицу объема;

dSdq - поверхностная плотность заряда - заряд, приходящийся на единицу

площади;

dqdl - линейная плотность заряда - заряд, приходящийся на единицу длины.

§ 8. Применение теоремы Гаусса к расчету полей.

8.1. Равномерно заряженная бесконечная плоскость.
Бесконечная	плоскость	заряжена	с
постоянной поверхностной		плотностью
заряда +σ. Линии напряженности
			E
перпендикулярны плоскости и направлены
от нее в обе стороны.
В качестве	замкнутой	поверхности

выберем цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна.

Полный поток через цилиндр: ФЕ=Фбок+Фосн1+Фосн2 Так как образующие цилиндра параллельны линиям напряженности, то поток

вектора E сквозь боковую поверхность цилиндра равен нулю. Площади оснований

равны. Проекция вектора E на основание: Еn=Е. Тогда полный поток: ФЕ=2ЕS.

Заряд, заключенный внутри цилиндра q S . По теореме Гаусса: 2ES S .

Отсюда напряженность поля равномерно заряженной бесконечной плоскости:

Eпл .

2 0

Видно, что напряженность не зависит от длины цилиндра, т.е. на любом расстоянии от плоскости одинакова. Таким образом, поле равномерно заряженной бесконечной плоскости однородно.

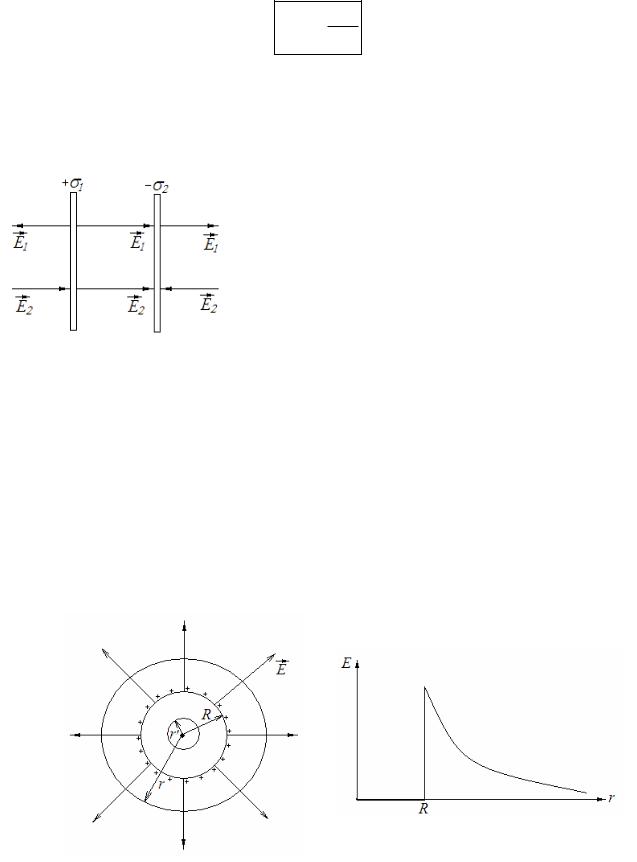
8.2. Поле двух бесконечных параллельных разноименно заряженных плоскостей.

						Плоскости					заряжены с						поверхностной
			плотностью:						1 , 2						.		Результирующее
			поле найдем, как суперпозицию полей,
			создаваемых						каждой						из		плоскостей					в
																				1
																				1
			отдельности: E E1										E2 ,			где	E1				-
			отдельности: E E1										E2 ,			где	E1		2 0		-
																			2 0
			напряженность поля первой плоскости,															E2				2

																					2 0
																					2 0
- напряженность поля второй плоскости.
	Как видно из рисунка поля слева и справа от плоскостей вычитаются, т.к.
												0 .
E1	E2 , поэтому результирующая напряженность									E		0 .

	В области между плоскостями векторы								E1		и			E2 сонаправлены и равны по
величине, поэтому результирующая напряженность:
	E E E	2			1			2								.



	1			2 0			2 0		2 0					2 0	0
				2 0			2 0		2 0					2 0	0

Поле сосредоточено между плоскостями и является в этой области

однородным.

8.3. Поле равномерно заряженной сферической поверхности радиуса R.

Благодаря равномерному распределению заряда q по поверхности сферы, поле

обладает сферической симметрией. Поэтому линии вектора E направлены радиально.

Выделим мысленно сферу радиуса r, имеющую общий центр с заряженной сферой. Если r>R, то внутрь попадает весь заряд q и по теореме Гаусса:

Ф		E 4 r 2	q	откуда E	1	q	.
	E		0		4 0
						r 2

Если замкнутая поверхность не содержит внутри зарядов r <R, то поле равно нулю. Вне поверхности поле убывает с расстоянием r, подобно полю точечного заряда.

Eсферывне	1	q	при r R;

	4 0	r 2

Eсферывнутри 0			при r <R.

8.4. Поле объемно заряженного шара.

Шар заряжен равномерно с объемной плотностью ρ. Поле вне шара подобно

точечному заряду:

4 0 r 2 . Внутри шара выберем сферу радиуса r

<R. Заряд,

попадающий

внутрь

этой

сферы

V 3 r

По

теореме Гаусса:

E4 r

3 r

. Отсюда напряженность:

4 0

3 0

. Учитывая, что

, получим: E

r .

3 0

4 0

Таким образом, поле вне шара как у точечного заряда, а внутри шара изменяется линейно с расстоянием r .

Eшаравне	1	q	при r R;	Eшаравнутри	1	q	r	при r >R.
	4 0	r 2			4 0	R3

8.5. Поле равномерно заряженного с линейной плотностью

бесконечного цилиндра

1 / 21 2 > Следующая >>>