Arkhiv_ZIP_-_WinRAR / Модуль 2_4 Формулы пр

ОСНОВНЫЕ ПОНЯТИЯ И ФОРМУЛЫ

I. Векторная алгебра

Вектор - направленный отрезок.

Векторы коллинеарными, если лежат на одной прямой, либо на параллельных прямых.

Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.

a b - два вектора равны, если они коллинеарны, имеют одинаковую длину и направление.

Линейные операции над векторами

Суммой a b двух векторов a и b называется вектор, идущий из начала вектора a в конец вектора b при условии, что начало вектора b приложено к концу вектора a (правило треугольника).

Свойства:

1˚. a b b a

2˚. a b c a b c

3˚. a 0 a

4˚. Для каждого вектора a существует противоположный ему вектор a a, такой, что

a a 0.

Разностью векторов a и b будет вектор a b , идущий из конца вектора b к концу вектора a.

Произведение a вектора a на

вещественное число обладает свойствами: 5˚. a b a b

6˚. a a a

7˚. a a

8˚. 1 a a

Линейная зависимость векторов. Геометрические критерии линейной зависимости

Линейной комбинацией векторов a1, a2, ..., an называют выражение:

152

			n		,
1a1	2a2 ... nan iai
			i 1
где 1, 2, ..., n - произвольные действительные числа.
Система векторов a1, a2, ..., an		называется		линейно зависимой, если

существуют действительные числа 1, 2, ..., n , такие, что хотя бы одно из них отлично от нуля, и выполняется равенство:

a		a	...	a	n	0.	(*)
1 1	2	2	n

В противном случае, т.е. если линейная комбинация (*) обращается в ноль только при всех i 0, i 1, ..., n, то система векторов называется линейно

независимой.

Если векторы линейно зависимы, то любой вектор может быть выражен в виде линейной комбинации остальных.

Геометрические критерии линейной зависимости

Система двух ненулевых векторов a1, a2 линейно зависима тогда, и только тогда, когда векторы коллинеарны.

Система трех векторов a1, a2, a3 линейно зависима тогда и только тогда, когда векторы компланарны.

Базис и координаты

Базисом в пространстве называются три некомпланарных вектора, взятые в определенном порядке.

Базисом на плоскости будем называть два неколлинеарных вектора на этой плоскости, взятые в определенном порядке.

Базисом на прямой будем называть любой ненулевой вектор этой прямой.

Каждый вектор может быть разложен по базису в пространстве и это разложение единственно.

Коэффициенты разложения вектора по базису называются координатами

вектора в данном базисе и в каждом базисе определяются однозначно: d a b c = , , .

При сложении двух векторов d1 и d2 их координаты (относительно любого базиса) складываются. При умножении вектора d1 на любое число все его координаты умножаются на это число.

Системой координат в пространстве называют совокупность базиса a, b, c и

некоторой точки, называемой началом координат.

Вектор OM , идущий из начала координат в точку M , называется радиусвектором точки M .

153

Координатами точки M , , называются координаты вектора OM .

Таким образом, координаты радиус-вектора OM и координаты точки M совпадают.

Ортонормированный базис. Декартова прямоугольная система координат

Пусть в качестве базиса выбраны три взаимно перпендикулярных вектора с длинами, равными единице.

Обозначения: i, j,k , i = j = k 1

Такой базис называется ортонормированным (ОНБ). Векторы i, j, k называются базисными ортами. Зафиксируем точку О – начало координат и отложим от

нее векторы i, j, k . Полученная система координат называется прямоугольной декартовой. Координаты любого вектора в этом базисе называются декартовыми координатами вектора:

Z

	z		M
	k	j	Y
	0
			y
	x i

X

a x,	y,z x i y j z k

Прямые линии, проведенные через начало координат по направлениям

базисных векторов, называются координатными осями: i – порождает OX ; j

– порождает OY ; k– порождает OZ . Координаты точки М (вектора OM ) в декартовой системе координат по осям OX , OY , OZ называются соответственно абсциссой, ординатой и аппликатой.

Декартовы прямоугольные координаты x, y, z вектора a равны проекциям

этого вектора на оси Ox, Oy, Oz соответственно; другими словами,

x npOX a

a

cos , y npOY a

a

cos , z npOZ a

a

cos .

Здесь ,

, – углы, которые составляет вектор a с координатными осями Ox,

Oy, Oz

соответственно, при этом

cos ,

cos ,

cos

называются

направляющими косинусами вектора a.

Вектор

a0

a

cos ,cos ,cos представляет собой

вектор

единичной

a

длины данного направления, или орт данного направления. Для направляющих косинусов справедливо соотношение:

cos2 cos2 cos2 1.

Проекция вектора a на ось l A B равна

154

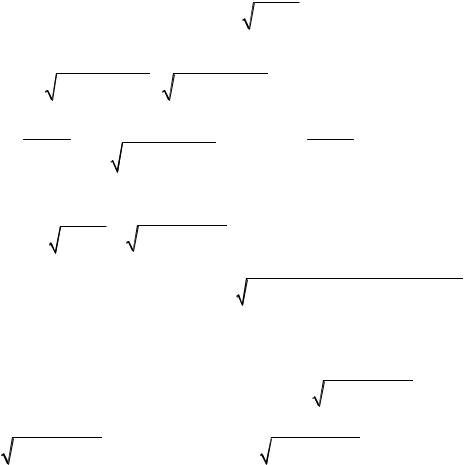
прl a

a

cos

a

cos(a, l0 ), где l0

- орт оси l.

Скалярным произведением двух векторов называется число, равное

произведению длин этих векторов на косинус угла между ними:

a b a,b a b

a

b

cos(a, b).

Если a x1,

y1, z1 ,

b x2,

y2, z2 ,

то a b x1x2

y1 y2

z1z2 .

Алгебраические и геометрические свойства:

1°. a b b a .

2°. a b a b a b

a

a c .

3°. a b c a c b c ,

b c a b

4°. a a 0, если a 0, и a a 0, если a 0.

5°. a a

a

a

cos a,a

a

2 cos0o

a

2 ;

a

a a

.

a b

x x y y

2

z z

2

6°. cos a, b

1

2

1

1

.

a

b

x12 y12 z12

x22 y22 z22

(a,b )

axbx

ayby azbz

a b

7°. прba =

a

прb a

,

прab

.

b

bx2 by2 bz2

a

8°. a b:

a

0 - условие перпендикулярности.

b

2

a

a a

9°. a x,

y,

z ,

x2 y2 z2

- длина вектора.

10°. A x, y,

z ,

B x ,

,

y ,

z

(AB)

AB

(x x )2

(y y )2 (z z )2

–

1

1

1

2

2

2

1

2

1

2

1

2

расстояние между двумя точками.

x

11°. Направляющие косинусы вектора: cos cos(a,i)

,

x2 y2

z2

y

z

cos cos(a, j)

, cos cos(a,k)

;

x2 y2 z2

x2 y2 z2

cos2 α + cos2 β + cos2

= 1

Упорядоченная тройка некомпланарных векторов a1, a2 , a3, приведенных к одному началу, называется правой, если из конца третьего вектора a3

155

кратчайший поворот первого вектора a1 ко второму a2 виден совершаемым против часовой стрелки. В противном случае тройка называется левой.

a3	a3
a2		a2
a1	a1
правая	левая
При перестановке местами двух соседних векторов ориентация тройки
меняется.
Если тройки a b c, b c a, c a b - правые, то a c b ,		c b a, b a c - левые.
При круговой (циклической) перестановке векторов ориентация тройки не
меняется.
Векторным произведением вектора a	на вектор	b называется вектор

c a, b a b a b , удовлетворяющий следующим трем требованиям:

1). Длина вектора c

равна произведению длин векторов a и b на синус

sin a,b .

угла между ними, т.е.

c

a

b

a b

2). Вектор c ортогонален к каждому из векторов a и b , т.е. c

перпендикулярен плоскости, в которой лежат векторы a и b .

3). Вектор c направлен так, что тройка a b c является правой.

Алгебраические и геометрические свойства:

1°. a b

b a .

2.

a b

a b .

3.

a b c

a c

b c .

4. a a 0 для любого вектора a.

5. S

пар

=

a b

6.

[a

b]

0

a коллинеарен b .

Если a x1,

y1,

z1 , b x2,

y2, z2 ,

c

a

b

y z

2

z y

2

, z x

2

x z

2

,

x y

2

y x

,

1

1

1

1

1

1 2

c

i

j

k

x

y

z

.

a b

1

1

1

x2

y2

z2

156

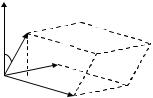
k k

0,

k,

i i

j j

i j j i

i k

k i

j,

j k

k j

i.

Если a x1,

y1, z1

и b x2,

y2,

z2 коллинеарны, то

x1

y1

z1

.

x2

y2

z2

Смешанное

произведение

некомпланарных

векторов

abc

b

c по

a

абсолютной величине равно объему параллелепипеда, построенного на этих векторах, приведенных к одному началу.

abc положительно, если тройка a, b , c правая и отрицательно, если она левая.

Если же векторы a, b , c компланарны, то a b c равно

x1

y1

z1

0.

нулю: abc

x2

y2

z2

x3

y3

z3

c

a

c a b ,

a b

c b

bac acb cba abc.

c

a

a

c

a b

c b

b

a

θ

c

0

b

смешанное произведение зависит от порядка сомножителей, но не зависит от того, какие сомножители связаны первичным знаком векторного произведения.

Если a xi

y j

z k ,

b x2i y2 j z2k , c x i y

j z k , то

1

1

1

3

3

3

x1

y1

z1

.

abc

x2

y2

z2

x3

y3

z3

II. Аналитическая геометрия в пространстве

Плоскость в пространстве

1.

Ax By Cz D 0

- общее уравнение плоскости в декартовой системе

A2 B2 C2

0

координат ;

2.

- уравнение плоскости, проходящей

A(x x0 ) B(y y0 ) C(z z0 ) 0

через заданную точку (x0 , y0 ,z0 ) и перпендикулярной вектору n {A,B,C};

157

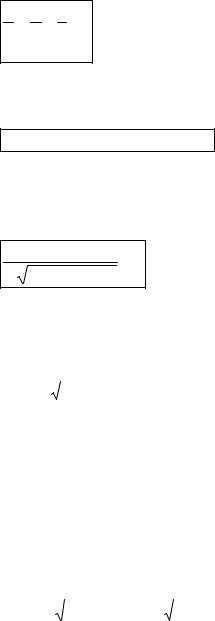
yz

3.a b c 1 - уравнение плоскости, отсекающей на осях координат ox, oy,

abc 0

oz отрезки a, b и c соответственно;

4. xcos ycos zcos p 0 - нормальное уравнение плоскости, где р – расстояние от начала координат до плоскости, а единичный вектор, перпендикулярный плоскости, имеет координаты {cosα,cosβ,cosγ};

5.	Ax By Cz D 0		- нормальный вид общего уравнения плоскости
		A2 B2 C2

(знак нормирующего множителя противоположен знаку D);

6.

d

Ax0

By0 Cz0

D

- расстояние от точки (x0 , y0 ,z0 ) до плоскости,

A2 B2

C2

заданной общим уравнением;

7.

x x1

y y1

z z1

- уравнение плоскости, проходящей через три

x2 x1

y2 y1

z2

z1

0

x3 x1

y3 y1

z3

z1

не лежащие на одной прямой;

точки (xi , yi ,zi )

(i=1,2,3),

8.

cos

A1 A2 B1B2 C1C2

- угол

между плоскостями

A2 B2 C2

A2

B2

C2

1

1

1

2

2

2

Ai x Bi y Ci z Di

0

(i 1,2) ;

9.

A1

B1

C1

-

необходимое и достаточное

условие параллельности

A2 B2 C2

плоскостей Ai x Bi y Ci z 0

(i 1,2);

10.

- необходимое и достаточное условие

A1A2 B1B2

C1C2 0

перпендикулярности плоскостей Ai x Bi y Ci z 0

(i 1,2);

158

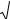
11.

d

D1 D2

-

расстояние между

двумя параллельными

A2 B2

C2

плоскостями Ax By Cz D1

0 и Ax By Cz D2

0.

Прямая в пространстве

12.

A x B y C z D 0

- общее уравнение

прямой как линии

1

1

1

1

A2 x B2 y C2 z D2 0

пересечения двух параллельных плоскостей;

13.

x x0

y y0

z z0

- канонические

уравнения прямой,

l

m

n

проходящей через точку (x0 , y0 ,z0 ) и имеющей направляющий вектор с

компонентами {l,m,n};

mx ly ly0 mx0 0

14.

ny0 0-

уравнения прямой

в

виде проекций на

ny mz mz0

nx lz lz0 nx0 0

координатные плоскости;

x x0

lt

15.

mt

- параметрические уравнения прямой, проходящей

y y0

nt

z z0

через точку (x0 , y0 ,z0 ) и имеющей направляющий вектор с компонентами

{l,m,n};

	l B1C2 B2C1
16.	m C1A2			C2 A1	- соотношения между компонентами направляющего
	n A B		2	A B
		1		2 1

	вектора прямой и координатами общего уравнения прямой;
17.			x x1		y y1		z z1		- канонические	уравнения прямой,
							z2 z1
			x2 x1		y2 y1					(i=1,2);
	проходящей через точки с координатами (xi , yi ,zi )

159

18.

cos

l1l2

m1m2 n1n2

- косинус угла

между прямыми

l2

m2

n2

l2

m2

n2

1

1

1

2

2

2

x x0

y y0

z z0

(i=1,2), проходящими через точку (x0 , y0 ,z0 );

li

mi

ni

19.

l1

m1

n1

-

условие

параллельности

двух

прямых

l2 m2

n2

x xi

y yi

z zi

(i=1,2);

li

mi

ni

20.

-

условие перпендикулярности двух прямых

x xi

l1l2 m1m2

n1n2

0

y yi

z zi

(i=1,2);

li

21.

mi

ni

x x1

y y1

z z1

x x2

y y2

z z2

Прямые: L1 :

l1

m1

n1

и

L2 :

l2

m2

n2

лежат в

одной плоскости, если

x2 x1

y2 y1

z2 z1

l1

m1

n1

0

l2

m2

n2

-

Прямая и плоскость в пространстве

22.

уравнение

пучка

A1x B1 y C1z D1 (A2 x B2 y C2 z D2 ) 0

плоскостей, проходящих через прямую, заданную общим уравнением

A1x B1y C1z D1 0A2x B2 y C2z D2 0.

x x0 lt1

y y0 mt1

23.

z z

0

nt , где

- координаты точки пересечения прямой

1

t

Ax0 By0 Cz0 D

1

Al Bm Cn

x x0

y y0

z z0

и плоскости Ax By Cz D 0;

l

n

m

160

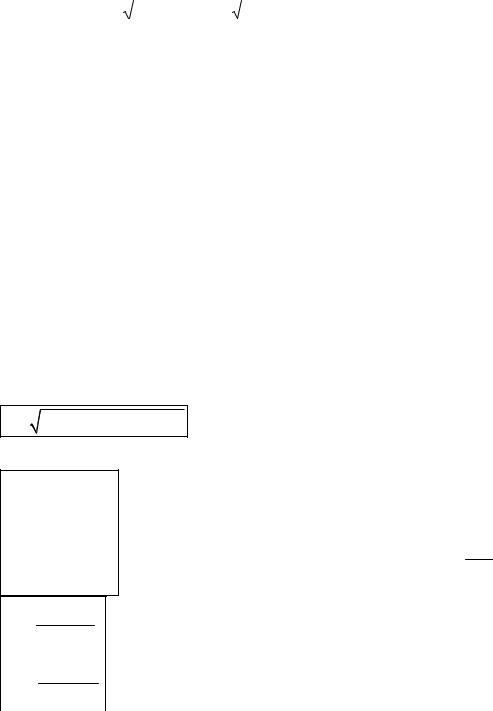
24.

sin

Al Bm Cn

- синус угла между

прямой

A2 B2 C2 l2 m2 n2

x x0

y y0

z z0

и плоскостью Ax By Cz D 0;

l

m

n

25.

-

условие

параллельности

прямой

Al Bm Cn 0

x x0

y y0

z z0

и плоскости Ax By Cz D 0;

l

m

n

26.

A

B

C

-

условие

перпендикулярности

прямой

n

l m

x x0

y y0

z z0

и плоскости Ax By Cz D 0.

l

m

n

III. Аналитическая геометрия на плоскости

Прямая на плоскости

1. d (x	2	x )2	(y	2	y )2
		1			1

		x x
	x	1	2	,
		1
2.		y1	y2
	y				,
		1
	1

x x1 x2 ; 2

3. y y1 y2

				2
		x1	y1	1
4.		x2	y2	1	0
		x3	y3	1

-расстояние между точками A(x1,y1) и

B(x2,y2);

-координаты точки С(x,y), которая делит отрезок, соединяющий точки A(x1,y1) и

B(x2,y2), в отношении AC ;

CB

-координаты середины отрезка АВ;

-условие принадлежности трёх точек

(x1,y1), (x2,y2), (x3,y3) одной прямой;

161