Reshenie tip priemov po matematike_ochnaya

РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ

РАСЧЕТНО–ГРАФИЧЕСКАЯ РАБОТА №1

1.Привести уравнения данных гармонических колебаний

у= 4sin 3x −3cos 3x

к виду у = Asin(ωx +ϕ).

Найти амплитуду А, фазу ϕ , период гармоники и построить ее график. Решение. Привести уравнения данных гармонических колебаний

у = 4sin 3x −3cos3x

к виду

у = Asin(ωx +ϕ),

где

А =

а2 +b2

– амплитуда,

ϕ = arctg b ,

sin ϕ =

b

, cosϕ

=

a

и

T =

2π

– период колебания.

A

ω

a

A

В нашем случае:

3

3

4

−

sin ϕ = −

, cosϕ =

, откуда ϕ

при-

А = 42 + (−3)2 , ϕ = arctg

4

и

5

5

надлежит 4 четверти и ϕ = −arctg 3

= −36,90

, T =

2π

=1200 . Тогда

у = 5sin(3x −36,90 ) ,

4

3

T =1200 .

От графика

функции

y = sin x

перейдем к

графику

функции

у = 5sin(3x −36,90 ) с помощью следующей цепочки преобразований:

y = sin x,

y

2

= sin 3x,

y

3

= 5sin 3x,

y = 5sin 3(x −12,30 ),

1

то есть к нашей функции у = 5sin(3x −36,90 ) .

Построение:

1.

Строим одну волну синусоиды y1

= sin x .

2.

Строим

график функции

y2 =sin3x , которая имеет

период

T=1200 (то есть сжимаем функцию y1 в три раза).

3.Увеличивая ординаты графика y2 в 5 раз, получаем график функ-

ции y3 =5sin 3x .

4.Сдвигаем график функции y3 на 12,30 вправо вдоль оси Ох.

у

5

1		1200		132,30
0	12,30	600		1800	3600	х
		у2=sin3x			у1=sinx
		у3=5sin3x	у=5sin(x–12,30)

44

хr	2. Даны векторы е1 = {1;2;1}, е2 = {− 2;3;−1}, е3 = {1;−1;24}				и
	= {1;8;−1}. Показать, что векторы е , е	2	, е образуют базис трехмерного
	1		3
пространства, найти разложение и координаты вектора хr в этом базисе.
Полученную систему линейных уравнений решить тремя методами:
	а) через определители (формулы Крамера),
	б) через обратную матрицу,
	в) методом Гаусса (через расширенную матрицу).			, еr
	Решение. Составим определитель из координат векторов еr				, е и
			1	2	3

вычислим его, разложив по элементам первой строки:

	1	2		1			3	−1						−2 −1			−2 3
	−2 3 −1				=1					− 2						+1		=
	1	−1		2			−1	2						1	2		1 −1
= 6 −1− 2(−4 +1) +(2 −3) =10 ≠ 0,
значит,			векторы				еr , еr , еr				образуют базис трехмерного пространства и
							1	2	3
вектор хr можно разложить по векторам базиса
		хr	= х1еr1 + х2еr2 + х3еr								,
где х1 , х2 ,				х3 – координаты вектора х в базисе {е1, е2 , е3}.
		Перейдем к матричной записи полученного векторного уравнения
			1		1			−			2				1
						2			3
			8	= х1			+	х2					+ х3		−1 .
						1			−		1
		−1													2

Используя свойства матриц и действия над ними, получим систему линейных уравнений относительно неизвестных х1, х2 , х3 :

х1 − 2х2 + х3 =1,2х1 +3х2 − х3 = 8,х1 − х2 + 2х3 = −1.

а) Решение полученной системы линейных уравнений через определители.

Находим главный определитель системы уравнений:

		1	− 2	1
∆ =		2	3	−1		=10 ≠ 0,
		1	−1	2

следовательно, данная система уравнений имеет единственное решение, которое находим по формулам Крамера:

x =

∆1

,

х

=

∆2

,

х

=

∆3

,

∆

1

∆

2

∆

3

45

где ∆i (i =1,2,3) получается путем замены i-го столбца свободными чле-

нами.

Вычислим определители ∆1, ∆2 , ∆3 .

	1				− 2			1
∆1 =	8				3			−1			= 6 −8 − 2 −(−3 +1−32) = 30,
	−1				−1			2
			1		1			1										1		− 2		1
∆2 =			2	8 −1						= 0, ∆3 =								2	3			8			= −20 .
			1		−1			2										1		−1		−1
Находим			x		=	30		= 3; х				2	=		0	= 0;				х	3	=	− 20			= −2.
				1	10									10								10
Ответ:				x1 = 3;				х2 = 0;							х3 = −2.

б) Решение системы через обратную матрицу.

Обозначим через А матрицу коэффициентов при неизвестных, Х – матрицу-столбец неизвестных Х1, Х2, Х3; Н – матрицу-столбец свободных членов:

1		− 2	1		Х		1			1
	2	3				Х				8
А =			−1 ,		Х =		2	,	Н =		.
	1	−1	2			Х
							3			−1

С учетом этих обозначений данная система уравнений принимает

следующую матричную форму:

А Х = Н .

Для нахождения решения системы уравнений необходимо вычис-

лить обратную матрицу

А

А

А

11

21

31

∆

∆

∆

А−1 =

А12

А22

А32

,

∆

∆

∆

А

А

А

13

23

33

∆

∆

∆

где Аij (i =1,2,3; j =1,2,3)– алгебраическое дополнение элемента aij .

Вычислим определитель ∆ и алгебраические дополнения Аij эле-

ментов матрицы А.

1

− 2

1

=10 ≠ 0, следовательно, матрица А имеет обратную

∆ =

2

3

−1

1

−1

2

матрицу А−1 .

46

А			= (−1)1+1						3													−1										=				5, А							= (−1)1+2														2 −1									= −5,
11										−1												2																12																		1						2
А = (−1)1+3												2								3									= −5,
13												1									−1
А			= (−1)2+1															− 2 1														= 3, А											= (−1)2+2														1 1							= 3,
21																			−1			2																22																			1		2
А = (−1)2+3																			1 − 2													= −1,
23																			1		−1
А			= (−1)3+1													− 2						1													= −1, А											= (−1)3+2															1	1							= 3,
31																		3				−1																					32																		2			−1
А = (−1)3+3																	1 − 2													= 7.
33																		2				3
Тогда																		5										3										1
																																				−
									10													10																10											5										3					−1
																																															1
				А−1 =			−												5									1										3												−5 1												3
																																											=																								.
																		10				10														10									10
																																																		−5 −1 7
							−												5			−						1										7
																		10										10								10
				Решение системы уравнений
																		1				5														3 −1 1																1										5 1+3 8 + (−1) (−1)
Х = А−1 Н =
																						−5 1 3																									8				=													−5 1+1 8 +3 (−1)							=
									10																																											10
																						−5 −1 7
																																															−1												−5 1+ (−1) 8 + 7 (−1)
					30															3
=	1				0	=														0		.
	10
					−20														− 2
Отсюда x1 = 3;																				х2 = 0;																х3 = −2.
				Ответ:			x1 = 3; х2 = 0;																																			х3 = −2.

в) Решение системы линейных уравнений методом Гаусса (через расширенную матрицу).

Составим расширенную матрицу данной системы линейных уравнений и с помощью элементарных преобразований матрицы приведем ее к треугольному виду (ниже главной диагонали все элементы равны нулю).

47

				х1		х2 х3
				1		− 2 1			1		1		− 2 1			1		1 − 2 1				1
В = (А			Н)=	2		3 −1			8		~	0	7	−3		6		~	0 1	1		− 2		~
				1		−1 2						0	1	1		− 2			0 7	−3		6
									−1
1		− 2		1		1
	0	1		1		− 2
~							.
	0		0 −10			20

Видим, что ранги матриц А и В совпадают и равны числу неизвестных, то есть r(A) = r(B) = 3, n = 3 . Следовательно, система линейных уравне-

ний имеет единственное решение. Чтобы найти это решение, перейдем от матричной записи к ступенчатой системе уравнений.

x1 − 2х2 + х3 =1,

2+ х3 = −2,

−10х = 20.

3х

Двигаясь снизу вверх (обратный ход метода Гаусса), получаем х3 = −2.

Полученный результат подставляем во второе уравнение, а потом вместе с найденным х2 в первое уравнение:

х2 − 2 = −2, х2 = 0,

х1 − 2 0 − 2 =1, х1 = 3.

Ответ: x1 = 3;

х2 = 0;

х3 = −2.

3. Определить тип кривой 9х2 + 25у2 = 225, найти ее параметры;

определить угловой коэффициент прямой

х

+

у

=1. Найти точки пере-

5

3

сечения данных линий и сделать чертеж.

Решение. Приведем уравнение кривой 9х2 + 25у2 = 225 к канони-

ческому виду

х2

+

y2

=1, разделив на 225. Получим уравнение эллипса

а2

b2

х2

y2

+

=1. Его большая полуось a = 5 ,

малая полуось

b = 3. Центр

25

9

совпадает с началом координат.

Уравнение прямой

х

у

=1 имеет вид «в отрезках»

х

у

+

+

=1 ,

5

3

b

а

что удобно для построения.

Для нахождения углового коэффициента

48

прямой приведем ее к виду y = kx +b , выразив у через х: у = −53 х+3 .

Угловой коэффициент k = −53 .

Для нахождения точек пересечения этих линий решим систему

9x2 + 25y2 = 225,5y = −3x +15.

Возведем второе уравнение в квадрат

25y2 = (−3x +15)2

и подставим в первое уравнение:

9х2 + (−3х+15)2 = 225, 9		х2 +9х2 −90х+ 225 = 225,
18х2 −90х = 0, 18х(х−5)		= 0,
х1 = 0,	х2 = 5,
у1 = 3,	у2 = 0.

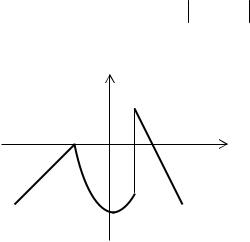
Нашли точки пересечения (0; 3) и (5; 0), что наглядно видно на чертеже.

у

3

–5

0

5

х

–3

4. Даны координаты вершин пирамиды АВСD: А(0;0;1), В(2;3;5),

С(6;2;3), D(3;7;2). Требуется:

1)записать векторы АВ, АС, АD в системе орт i , j, k и найти модули этих векторов;

2)найти угол между векторами АВ и АС ;

3)найти проекцию вектора АD на вектор АВ;

4)найти площадь грани АВС;

5)найти объем пирамиды АВСD;

6)составить уравнение ребра АС;

7)составить уравнение грани АВС.

49

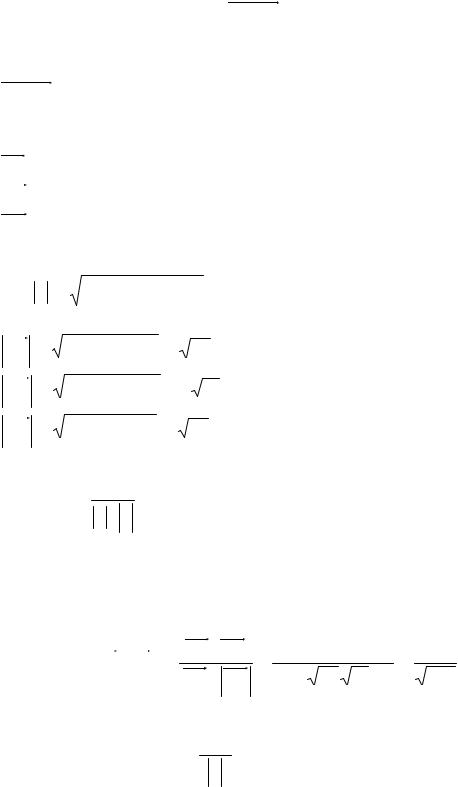
Решение.	rj, kr по
1) Произвольный вектор а представляется в системе орт ir,

формуле r

аr = ахir + ay j + az k ,

где ax , ay , az – координаты вектора а. Если заданы точки M1(x1, y1, z1 ),

M 2 (x2 , y2 , z2 ), то для вектора аr = M1M 2 ax = x2 − x1, ay = y2 − y1, az = z2 − z1 ,

то есть
M1M 2 = (x2 − x1 )ir + ( y2 − y1 ) rj + (z2 − z1 )k .
Воспользовавшись формулой и координатами заданных точек А,
В, С, D, получим:
АВ = (2 −0)i + (3 −0) rj + (5 −1)k = 2i +3 j + 4k ;
АС = (6 −0)i + (2 −0) rj + (3 −1)k = 6i + 2 j + 2k ;
АD = (3 −0)i + (7 −0) j + (2 −1)k = 3i + 7 j + k .
Если вектор					аr = ахir + ay j + az k , то его модуль вычисляется по
формуле: аr =		ах		2 + ay			2 + az	2 .
Модули найденных векторов
АВ = 22 +32 + 42 = 29 ;
АС = 62 + 22 + 22 = 2 11 ;
АD = 32 + 72 +12 = 59 .
2) Известна формула
r r				r	r
			a		b
cos a,b		=	a		r	,
					b

где ar br – скалярное произведение векторов а и b , которое можно вы-

числить следующимr образом: ar b = axbx + ayby + azbz .

У нас

				AB AC		= 2 6 +3 2 + 4 2 =	13 ≈ 0,7279 ,
cosϕ = cos AB, AC			=
				AB	AC	2 29 11	319

то есть ϕ ≈ 430 .

3) Известно, что прbrar = arbrb ,

50

то есть в нашем случае
					r r
прAB	AD = a rb =					2 3 +3 7	+ 4 1	=	31	≈ 5,76 .
					b	29			29
4) Воспользуемся формулой нахождения площади треугольника,
построенного на векторах a и b
1		r	r
S = 2		a	×b		,

		r	r		ir		rj	kr
		a ×b			= ax	ary		az .
					bx	by		bz
	В нашем примере S∆ABC =									1	AB × AC , причем
									2
						ir	rj	kr
		AB × AC = 2 3 4 = 2(−ir +10 rj −7kr) .
						6	2	2
	Таким образом, S∆ABC							= 1	2 (−1)2 +102 + (−7)2 = 150 = 5 6 (кв. ед.).
								2
	r	5) Объем пирамиды, построенной на трех некомпланарных векто-
		r	r	можно найти по формуле
	рах a, b		, c
	где ar	V =		1	r	r	r
				6 (a ×b)			c ,
		×b – векторное произведение векторов, которое можно вычислить
	по следующему правилу:

где (ar×b) cr

– смешанное произведение векторов, которое вычисляется

следующим образом:

r

r

r

ax

ay

az

bx

by

bz

.

(a ×b) c =

cx

cy

cz

У нас V =

1

(АВ× АС) AD

, где

6

2

3

4

(АВ× АС) AD =

6

2

2

= 2(2 −14) −3(6 −6) + 4(42 −6) =120 ,

3

7

1

то есть V = 1

120 = 20 (куб. ед.).

6

51

6) Известно, что уравнение прямой, проходящей через две заданные точки M1(x1, y1, z1 ) и M 2 (x2 , y2 , z2 ), имеет вид:

x − x1			=	y − y1			=	z − z1			.
x	2	− x		y	2	− y		z	2	− z
		1				1				1

Подставив координаты точек А и С, получим:

	x −0	=	y −0	=	z −1		,
	6 −0		2 −0		3 −1

то есть уравнение ребра АС окончательно запишется следующим образом:

x

=

y

=

z −1

или

x

=

y

=

z −1

.

6

3

2

2

1

1

7) Уравнение плоскости, проходящей через три заданные точки

A(x1, y1, z1 ),

В2 (x2 , y2 , z2 ), С1(x1, y1, z1 ), можно записать в виде

x − x1

y − y1

z − z1

x2 − x1

y2 − y1

z2 − z1

= 0 .

x3 − x1

y3 − y1

z3 − z1

Подставляя в него координаты точек А, В, С, получим:

x −0

y −0 z −1

x y z −1

2 −0

3 −0 5 −1

= 0;

2 3

4

= 0;

6 −0

2 −0 3 −1

6 2

2

х(−2) − у(−20) + (z −1)(−14) = 0; −2x + 20y −14z +14 = 0;

x −10y + 7z −7 = 0.

РАСЧЕТНО–ГРАФИЧЕСКАЯ РАБОТА №2

5. Функция у задана различными аналитическими выражениями для различных областей изменения аргумента х:

х+ 2,		х ≤ −2,
	2 − 4,	− 2 < x <1,
у = x
4	− 2x,	x ≥1.

Требуется:

1)найти точки разрыва функции, если они существуют;

2)найти односторонние пределы и скачок функции в точках разрыва;

3)сделать чертеж.

52

Решение. Данная функция определена и непрерывна в интервалах (−∞;−2), (−2;1), (1;+∞) . При х = −2 и х =1 меняется аналитическое вы-

ражение функции, и только в этих точках функция может иметь разрыв. Определим односторонние пределы в точке х = −2 :

lim	y = lim (x + 2) = 0;	lim	y = lim (x2 − 4) = 0.
x→−2	x→−2	x→−2	x→−2
x<−2	x<−2	x>−2	x>−2

Односторонние пределы совпадают. Функция в этой точке непрерывна. Определим односторонние пределы в точке х =1:

lim y = lim(x2 − 4) = −3;		lim y = lim(4 − 2x) = 2.
x→1	x→1	x→1	x→1
x<1	x<1	x>1	x>1

Так как односторонние пределы функции у в точке х =1 не равны между собой, то в этой точке функция имеет разрыв первого рода.

Скачком функции в точке разрыва называется абсолютная величина разности между ее правым и левым предельными значениями. Следовательно, в точке х =1 скачок функции ∆ = 2 −(−3) = 5.

Построим график функции.

у

0

х

	6. Провести полное исследование функции	у =	х2	+ 20	методами
			х− 4

дифференциального исчисления и построить ее график. Решение.

1)Область определения функции

D( y) ={x (−∞;4) U(4;+∞)}.

2)Исследование на непрерывность и классификация точек разры-

ва.

Заданная функция непрерывна всюду, кроме точки х = 4. Вычислим ее односторонние пределы в этой точке:

	lim	f (x) = lim		x2	+ 20	= −∞;
				x − 4
	x→4−0	x→4−0
	lim	f (x) = lim		x2	+ 20	= +∞.
				x − 4
	x→4+0	x→4+0

53