mu

Вариант № 19

1. Найдите пределы, не пользуясь правилом Лопиталя:

1.1. lim

6x2 −7x −13

;

1.5. lim

7x +6x2 −16

;

x2 + 2x +5

5x −8 − x2

x→−1

x→∞

cos2 5x

4 +

3x

x

1.2. lim

;

1.6. lim

4

;

2

x→−π 2x

x→0

2 −

3x

1.3. lim

4x −7

;

1.7. lim

x3

+ 27

;

x2 + 2x −8

x→2

x→−3 x2 − x −12

1.4. lim

8x7 −16x8 +6

;

1.8. lim

x

2

−

x

8

2

.

6x

− 2x

−

5

2x

2

−1

2x +1

x→∞

x→∞

2. Исследуйте функцию на непрерывность, постройте её график:

x, если

x ≤ 0,

3

2.1. f (x) =

x

−2,

если

0 < x ≤ 2,

2.2. y =

.

3x

− x2

− x

2

,

если

x > 2.

4

3. Найдите производную функции:

3.1. y =

x6

−

4

+

x3

+e−2 tg5 ;

3.4. y = ctg x 10−2 x ;

x4

18

3

2

3.2. y =

x3

;

3.5. y = ctg

3

x

;

1−ln(4x)

3

3.3. y =

3 −4x

−e−8 x ;

3.6. y = log43 (2x2 −5x) .

5

4. Найдите пределы, пользуясь правилом Лопиталя:

x3 −3x + 2

2

8x

4.1. lim

;

4.3. lim

−

;

x

3

− x

2

− x +1

x

2

+ 2x −

x→−2

x→1 x −1

3

4.2. lim

1−cos 2x

;

4.4. lim

4x3 +9

.

cos7x

−cos3x

2 − x3 +5x2

x→0

x→∞

5. Найдите наибольшее и наименьшее значения функции на указанном отрезке:

	5.1. y =3x4 + 4x3 +1, [−2;1];	5.2. y = x +	4		, [−2; 0].
			x −1
	6. Найдите интервалы монотонности и экстремумы функции:
	6.1. y = 1 x3 −3x2 +8x ;	6.2. y = (2x +3) e−x .
	3

31

Вариант № 20

1. Найдите пределы, не пользуясь правилом Лопиталя:

1.1. lim

x2 +5x −6

;

1.5. lim

x9 − x5 −4

;

x2 −8x + 2

4x5

− 3 x 9

x→1

x→∞

1.2. lim

sin2 3x

;

1.6. lim

3 −6x

2 x+3

;

2

x→−π 3x

x→0

2 − x

1.3. lim

3 + x

;

1.7. lim

x2 +5x −6

;

x2 + x −6

x→−3

x→−6 x2 + 4x −12

1.4. lim

x3 −3x2 + 4

;

1.8. lim

1

−

1

.

4x

2

−6x

5

−3

2

−4

x

2

+3x

x→∞

x→−2 x

+ 2

2. Исследуйте функцию на непрерывность, постройте её график:

x −1,

если

x ≤1,

x

+ 4

2.1. f (x) =

x,

если

1

< x ≤ 4,

2.2. y =

.

4x

− x2

− x,

если

x > 4.

6

3. Найдите производную функции:

3.1. y =

2

−5

x5

−

3

−ln10;

3.4. y = tg x e−0,5ctg2 x ;

x4

2x

3.2. y =

sin 4x

;

3.5. y = 4 arcsin3 (2x +5) ;

3 +cos 2x

3.3. y =

2x −7

−cos

x

;

3.6. y = ln5 (x2 −2x) .

3

4

4. Найдите пределы, пользуясь правилом Лопиталя:

4.1. lim

x3 −6x2 +12x −8

;

4.3. lim

1

−

1

;

x

3

−3x

2

+14

x→2

x→π

2

cos x

ctg x

4.2. lim

1−cos5x

;

4.4. lim

3x3 −2x

.

e−x

2

−1

−8x3 −

5

x→0

x→∞ x2

5. Найдите наибольшее и наименьшее значения функции на указанном отрезке:

	5.1. y = x4 −8x2 −9 , [0;3];		5.2. y = x +	1	, [−5; −2.5] .
				x + 2
	6. Найдите интервалы монотонности и экстремумы функции:
	6.1. y = 1 x5 −	4x3 ;	6.2. y = (4x +3) ex 2 .
	5	3

32

4.2.2. Решение типового варианта и образец оформления индивидуального задания № 1

Индивидуальное задание № 1

Вариант 0

1. Найдите пределы, не пользуясь правилом Лопиталя:

1.1. lim

x2

−3x −10

;

1.5. lim

x7

− x5

+1

;

x2 + x −3

6x6

+ x7 −4

x→−2

x→∞

sin2

x

6 −5x

−3x

1.2. lim

2

;

1.6. lim

;

4x

2

+3x

x→π/2

x→0

3

1.3. lim

x −3

;

1.7. lim

x2

+ 4x −5

x2

+ x −

6

x2

+3x

−10

x→−3

x→−5

1.4. lim

x3 + 2x2 −7

;

1.8. lim

1

−

1

.

4

−3x

3

−

2x

2

−9

x

2

− x −6

x→∞ 5x

x→3

x

Решение

1.1. lim

x2 −3x −10

=

(−2)2 −3(−2) −10

=

4 + 6 −10

=

0

= 0 ;

x2

+ x −3

(−2)2

−2 −

3

4 − 2 −3

−1

x→−2

sin

2

x

sin

2 π

2

2

2

1

2

4

1.2.

lim

=

=

=

;

4x

π2

2π2

x→π/ 2

2

4

π2

4

1.3. lim

x −3

−3 −3

−6

= ∞;

=

=

2

+ x −6

(−3)

2

−3 −

6

x→−3 x

0

x3

+ 2x2 −7

m =3,

1.4.

lim

=

n = 4,

= 0 ;

5x4

−3x3 −2x

x→∞

m < n

x7

− x5 +1

m = 7,

1

1.5.

lim

=

n = 7,

=

=1;

6x6

+ x7 −4

1

x→∞

m = n

33

1.6.			6 −5x −3x		6 −5 0 −3 0		6 0
	lim			=		=		=1;
	x→0		3 +3x		3 +3 0		3

1.7. lim

x2

+4x −5

=

(−5)2 +4 (−5) −5

=

25 −20 −5

=

+3x −10

(

−5)2 +3 (−5) −10

25 −15 −10

x→−5 x2

0

x2 +4x −5 = (x +5) (x −1)

(x +5)

(x −1)

=

=

=

2

= (x +

5) (x −2)

= lim

x

+3x −10

(x +5)

(x −

2)

0

x→−5

= lim

x −1

=

−5 −1

=

6

;

x −2

x→−5

−5 −2 7

1

1

1

1

1.8. lim

−

=

−

=(∞ −∞)=

2

−

9

x

2

0

x→3

x

− x −6

0

2

−9 = (x −3)(x +3)

1

1

=

x2

= lim

−

=

− x −6 = (x −3)(x + 2)

(x −3)(x + 2)

x

x→3

(x −3)(x +3)

(x + 2) −(x +3)

−1

−1

= lim

= lim

=

= ∞.

(x

−3)(x +3)(x + 2)

x→3 (x −3)(x +3)(x + 2)

x→3

0

2. Исследуйте функцию на непрерывность, постройте её график:

−1,

если

x

≤ 0,

2x

2.1. f (x) =

x

−1,

если

0 < x ≤9,

2.2. y =

.

x2 −4x +

3

если

x >9.

x −4,

Решение

−1,

если

x

≤ 0,

2.1. f (x) =

x

−1,

если

0 < x ≤9,

если

x >9.

x −4,

Область определения данной функции D( y) = (−∞; +∞) . В точках

x = 0

и x = 9

функция меняет свой способ задания. В этих точках воз-

можен разрыв.

f (x) в точке x = 0 :

Исследуем на непрерывность функцию

f (0) = −1

f (0 −0) = lim

f (x) = lim(−1) = −1;

x→0−0

x→0

f (0 +0) = lim

f (x) = lim(

x −1) = −1.

x→0+0

x→0

34

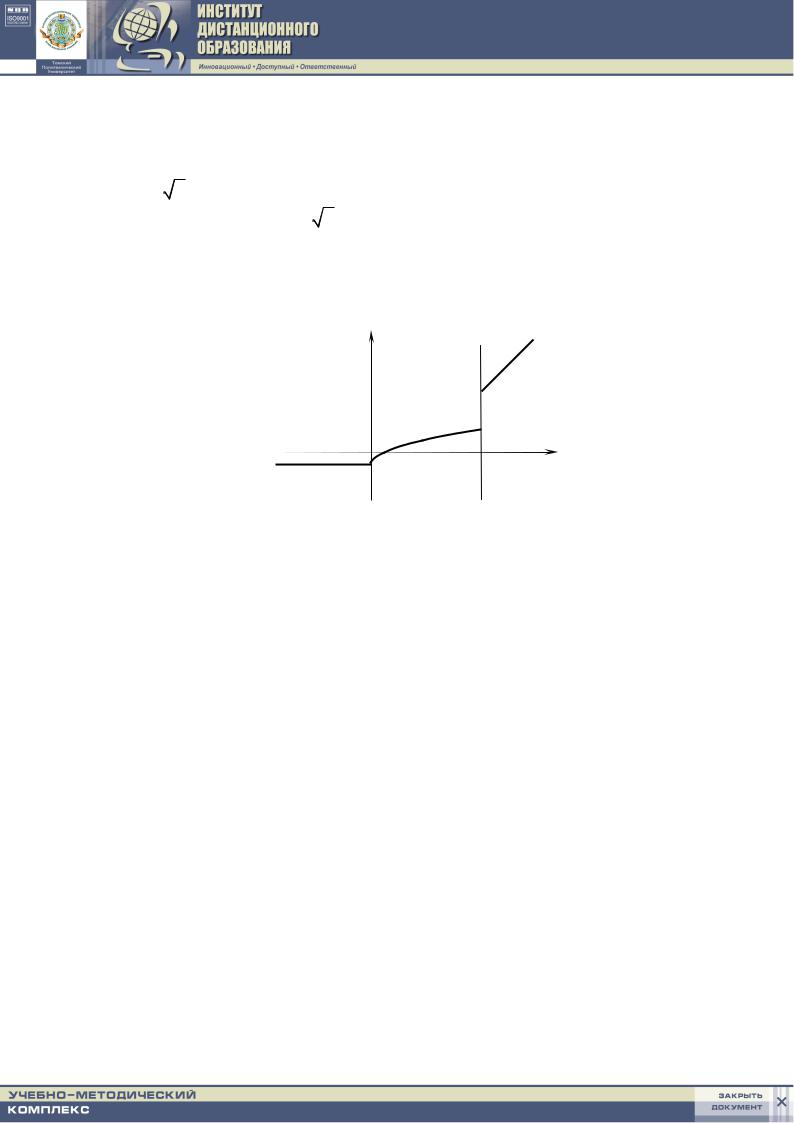
Так как f (0 −0) = f (0 +0) = f (0) = −1, заключаем, что f (x) непрерывна в точке x = 0 .

Исследуем на непрерывность функцию f (x) в точке x = 9 :

f (9) = 9	−1 = 2
f (9 −0) = lim		f (x) = lim( x −1) = 2 ;
	x→9−0	x→9
f (9 +0) = lim		f (x) = lim(x −4) = 5.
	x→9+0	x→9

Так как f (0 −0) ≠ f (0 +0) , но оба предела конечны, заключаем, что f (x) в точке x = 9 терпит разрыв 1 рода.

y

f(x)

	0				x
	- 1			9
2.2.	y =	2x
			.
		x2 −4x +3

Данная функция определена для всех значений x , для которых x2 −4x +3 ≠ 0 , т.е. x ≠1 и x ≠ 3 .

Во всех точках своей области определения D( y) = \ {1;3} функция

непрерывна. Точки x =1 и x =3 являются точками разрыва, так как в этих точках функция не определена.

Определим тип точки разрыва x =1. Для этого находим односторонние пределы:

lim

2x

= lim

2x

=

2 (1 −0)

=

2

= +∞;

x2 − 4x +3

(x −1)(x −3)

(1−0 −1)(1−0 −3)

−0

(−2)

x→1−0

x→1−0

lim

2x

= lim

2x

=

2 (1+0)

=

2

= −∞;

x2 −4x +3

(x −1)(x −3)

(1+0 −1)(1+0 −3)

+0

(−2)

x→1+0

x→1+0

Односторонние пределы равны бесконечности, следовательно, в

точке x =1 разрыв 2-го рода.

Определим тип точки разрыва x = 3 . Для этого находим односто-

ронние пределы:

lim

2x

= lim

2x

=

2 (3 −0)

=

6

= −∞;

x2 −4x +3

(x −1)(x −3)

(3 −0 −1)(3 −0 −3)

2 (−0)

x→3−0

x→3−0

35

lim

2x

= lim

2x

=

2 (3 +0)

=

6

= +∞;

x2 −4x +3

(x −1)(x −3)

(3 +0 −1)(3 +0 −3)

2 (+0)

x→3+0

x→3+0

Односторонние пределы равны бесконечности, следовательно, в

точке x = 3 разрыв 2-го рода.

Исследуем поведение функции на бесконечности

2x

m =1

2x

m =1

lim

=

n = 2

= −∞,

lim

=

n = 2

= +∞.

−4x +3

−4x +3

x→−∞ x2

m < n

x→+∞ x2

m < n

Вычислим значения функции в некоторых точках:

x	-2	-1	0	2	4	5
y	-0,27	-0,25	0	-4	2,67	1,25

y

0 1 3

- 4

3. Найдите производную функции:

	3.1.	y = −	4	+33 x −	x	−ln(cos3) ;
			x4		2

3.2.y = cos3x + 4 ; sin 3x

3.3.y = e3x 4 + 4x3−5 ;

Решение

x

3.4.y = tg x 5−0,5cos2 x ;

3.5.y = 4 arctg(2x −1) ;

3.6.y = log43 (3x − x2 ) .

3.1. y = −

4

+33 x −

x

−ln(cos3) ;

x4

2

4

x

′

4 ′

′

x ′

y′=

−

+

33

x −

−ln(cos3)

=

−

+(33

x )

−

−

x

4

2

x

4

2

36

−(ln(cos3))′ = −4(x

−4

′

+3(x

1

′

1

(x

1

′

−5

−2

1

−1

)

3 )

−

2

2 ) −0 =16x

+ x

3

−

4 x

2

;

3.2. y = cos3x + 4

;

sin 3x

cos 3x +

4

′

(cos 3x +4)′sin 3x −(cos 3x +4)(sin 3x)′

y′= y

=

=

(sin 3x)

2

=

sin 3x

=

−3sin 3x sin 3x −(cos3x +4)3cos3x =

−3sin2 3x −3cos2 3x −12cos3x

(sin 3x)2

(sin 3x)2

=

−3 −12cos3x ;

(sin 3x)2

3.3. y = e3x 4 +

4x −5

;

3

3x

4x −5

′

3x

′

4x −5

′

3

3x

4

y

′=

e

4 +

=

(e

4 )

+

=

e

4 +

;

3

3

4

3

3.4. y = tg x 5−0,5cos2 x ;

y′= (tg x 5−0,5cos2 x )′ = (tg x)′5−0,5cos2 x + tg x (5−0,5cos2 x )′ =

= cos12 x 5−0,5cos2 x + tg x 5−0.5cos2 x ln 5 (cos x sin x).

3.5. y = 4 arctg(2x −1) ;
y′= (4 arctg(2x −1) )′=			1	′		1		−	3				2
		(arctg(2x −1))4					(arctg(2x −1))
					=				4						;
						4					1		+(2x −1)	2

3.6. y = log43 (3x − x2 ) .

3		2	′		2		2		3 − 2x
y′=(log4	(3x − x		))	=3log	4	(3x − x		)				.
									(3x − x	2	)ln 4

37

4. Найдите пределы, пользуясь правилом Лопиталя:

4.1. lim

x3 + 2x −3

;

4.3. lim

1

−

x

;

x + x

2

x+3

−1

x

2

−9

x→1

x→−3

e

4.2. lim

1 −cos5x

;

4.4. lim

x3 + 4x2 −3x + 6

.

sin2 2x

x2 +5x3 − x

x→0

x→∞

Решение

4.1.

x3 +2x −

(x

3 +2x −3)′

3x2 +2x

3 12 +2 1

3

0

lim

=

= lim

= lim

=

= −5 ;

x − x2

(x − x2 )′

1−2x

1−2 1

x→1

0

x→1

x→1

4.2.

1−cos5x

(1−cos5x)′

5sin 5x

0

lim

= lim

= lim

=

=

sin2 2x

(sin2 2x)′

2sin 2x cos 2x 2

x→0

x→0

x→0

0

=

5

lim

(sin 5x)′

=

5

lim

5cos5x

=

5

5

=

25

cos 2x −2sin 2x sin 2x

4

2

8

4 x→0 (sin 2x cos 2x)′

4 x→0 2cos 2x

4.3.

x

x2 −9 − xex+3 + x

lim

1

−

={∞−∞}= lim

=

0

=

x+3

−1

x

2

−9

(e

x+3

−1)(x

2

−9)

x→−3

e

x→−3

0

= lim

(x2 −9 − xex+3 + x)′

= lim

2x −ex+3 − xex+3 +1

x+3

′

2

x+3

2

′

x+3 2

x+3

(e

−

−1)(x

−9)

e

(x

−9) +(e

−1) 2x

x→−3

x→−3

=

2 (−3) −1+3 1+1

=

−3

= ∞;

1 0

+0

(−6)

0

4.4.

x3 +

4x2 −3x +6

(x3

+4x2 −3x

+6)′

3x2 +8x

lim

=

∞

= lim

= lim

−3

=

x2 +5x3 − x

(x2 +

5x3 − x)′

2x +15x2 −1

x→∞

∞

x→∞

x→∞

∞

(3x2 +8x −3)′

6x +8

∞

(6x

+8)′

6

=

= lim

= lim

=

= lim

= lim

∞

(2x +15x2 −1)′

2 +30x

(2 +

30x)′

30

x→∞

x→∞

∞

x→∞

x→∞

=

1

.

5

;

=

=

38

5. Найдите наибольшее и наименьшее значения функции на указанном отрезке:

5.1. y = x3 −3x2 + 4 , [1;3]

y =

4x −1

, 5.2. [−1; 3] .

x2 +3

Решение

5.1. y = x3 −3x2 +4,

[1; 3].

Найдем производную данной функции

y

′

=

(x

3

−3x

2

+

′

=3x

2

−6x .

4)

Решим уравнение y′= 0

3x2 −6x = 0 3x(x −2) = 0 x = 0, x = 2 ;

x = 0 [1;3];

x = 2 [1;3]

Вычислим значение функции в точке x = 2

и на концах отрезка,

т.е. при x =1 и x =3

y(1) =13 −3 12 +4 = 2 ,

y(2) = 23 −3 22 +4 = 0 ,

y(3) =33 −3 32 + 4 = 4 .

Следовательно,

yнаиб. = 4, yнаим.

= 0 .

5.2. y =

4x −1

,

[−1;3].

x2 +3

Найдем производную данной функции

y′=

4x −1 ′

=

4(x2 +3) −(4x −1) 2x

=

4x2

+12 −8x2 +2x

=

2

(x

2

+3)

2

(x

2

+

3)

2

x

+3

=

−4x2

+2x +12

.

(x

2

+3)2

Решим уравнение y′=0

−4x2 +2x +12

= 0

−4x

2

+2x +12 = 0 ;

(x2 +

3)2

2x2 − x −6 = 0 ,

D =1+48 = 49 ,

x =

1±7

x1 = −1,5

1,2

4

x2 = 2

x1 = −1,5 [−1;3];

x2

= 2 [−1;3].

39

Вычислим значение функции в точке x = 2 и на концах отрезка,

	т.е. при	x = −1 и x =3
	y(−1) =	4 (−1) −1		= −	5	;
		(−1)2 +3			4

y(2) = 4222+−31 = 77 =1; y(3) = 4323+−31 = 1211 .

Следовательно,

yнаиб.

=1, yнаим.

= −

5

.

4

6. Найдите интервалы монотонности и экстремумы функции:

6.1. y =

x2 + 4

;

6.2. y = x e−x2 .

2x

Решение

6.1. y =

x2 + 4

.

2x

функции D( y) = (−∞; 0) U(0; +∞) .

Область

определения данной

Находим производную

x

2

+

4

′

(x

2

′

2x −(x

2

+ 4)

′

y′=

=

+ 4)

(2x)

=

2x

(2x)

2

=

2x 2x −(x2 +4) 2

=

4x2

−2x2 −8

=

2x2 −8

=

2(x2 −4)

=

x2 −4

.

4x2

4x2

4x2

4x2

2x2

Критическими точками функции являются те точки, в которых

производная равна нулю или не существует, т.е.

2

2−4 = 0,

(x −2)(x +2) = 0,

x

2x

≠ 0

{x ≠ 0.

Из системы следует, что производная равна нулю в точках x1 = −2 ,

x3 = 2 и не существует в точке x2 = 0 .

+

-

0

-

+

- 2

2

′

x2 −4

(−3)2

− 4

5

y (−3) =

=

2

=

>

0 ;

2x

2

2(−3)

18

x=−3

40