DisMathTPU_new

9.5. Упражнения

Упр.1. Определить, являются ли конъюнкции K1 K3 импликан- тами булевых функций f1 f3, по определению импликанты.

f1(a; b; c; d; e) = (a (b c) d) ! e,

K1 = a b c,

f2(a; b; c; d; e) = a e _

_ a c _ b d e,

K2 = a c d,

b

a

c

K3 =

e,

f3(a; b; c; d; e) = ((a=b) !

) # (c d).

c

e

Упр.2. Из заданных множеств конъюнкций выделить простые им- пликанты функций f1 f3, представив их матрицами Грея:

fac; a b; a c; ag; f1(a; b; c) = 00101111; fa b; b c; ag; f2(a; b; c) = 01111110;

fb d; b c; a b cg; f3(a; b; c; d) = 1010111001011110:

Найти все простые импликанты функций f1 f3.

Упр.3. Найти сокращенную ДНФ, все кратчайшие ДНФ и все безызбыточные ДНФ следующих булевых функций:

c

c

c

d

d

d

b

b

b

a

a

a

Óïð.4. Íàéòè ïî îäной кратчайшей ДНФ булевых функций.

c						c
d						d
e						e

b

b

a

a

Упр.4. Найти ДНФ функций, заданных формулами F1 F4, ïîä- становкой кратчайших ДНФ элементарных функций. Проверить правильность вычислений построением таблиц истинности или сравнением с результатами из упр. 6 подраздела 8.6.

F1	= x ! y		! x
		z				y;
F2 = x y - (x z);
					) ,! y _ z;
F3 = y # (x yz

F4 = x y=(z y) _ (x t y).

61

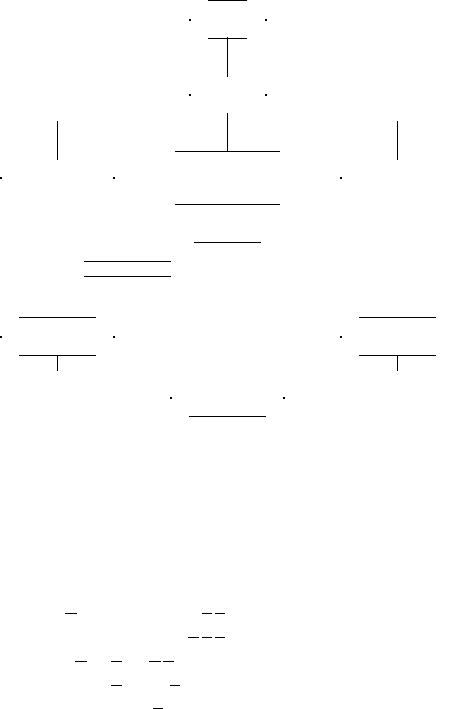
10. Контрольная работа 2

Тема контрольной работы: дизъюнктивная нормальная форма,

совершенная, сокращенная и кратчайшая ДНФ.

F

разложением

0

подстановкой

'

(F )

$

по переменным

?

КратДНФ

3

1

5

ÄÍÔ

таблица

ÄÍÔ

?

#

?

?

0

истинности

00

"

!

40

4

-

#2

?

&

%

матрица

'

Ãðåÿ

$

"

!

?

?

6

6

8

400

СокрДНФ

-

КратДНФ

7

70

&

СовДНФ

%

Схема контрольной работы (решение каждой из двенадцати задач начинать с постановки задачи и делать вывод из сравнения матриц Грея, полученных разными способами; F обозначает формулу

без лишних скобок, (F ) с недостающими скобками).

Задания на контрольную работу (формула F )

1)x ! y ! (x z) ! xy _ x y z

2)z ! y ! (z x) ! yz _ x y z

3)x ! yz ! (x z) _ x y z

4) yz x ! (x z) _ xyz 5) z y ! (x # yz) _ x y z

6) y

x ! (

x) ! xy _

z

x

y

z

7) yz

x ! (z x) _ x

z

y

8) x ! yz ! (x z) _

z

x

y

9) z y ! (

yz) _

x

x

y

z

10) x

yz=(x y) _ xyz

62

11)xy ! z=(z y) _ xyz

12)z y ! (x # yz) _ xyz

13)y z ! (yz ! x) _ x y z

14)y x ! (z x) ! xy _ x y z

15)x yz ! (x y) _ xyz

16)x yz ! (x y) _ xyz

17)z y ! (yz ! x) _ xyz

18)yz=x ! (x y) _ xyz

19)xy ! z=(z y) _ xyz

20)z y ! (x # yz) _ x y z

Пример. Задана формула

21) x yz=(x y) _ xyz 22) z y ! (x yz) _ xyz

23)xy ! z=(z y) _ xyz

24)yz=x ! (x y) _ xyz

25)x=y ! (x z) ! xy _ x y z

26)x=y ! (x z) ! xy _ x y z

27) yz x ! (z x) _ x y z

28)y x ! (z x) ! xy _ x y z

29)z y ! (yz ! x) _ x y z

30)yz ! x=(x z) _ xyz

F= x ! yz=(y z) _ xyz:

0)Расставим скобки в формуле F . Возьмем в скобки конъюнкции, затем остальные подформулы слева направо.

(F ) = ((x ! (yz))=(y z)) _ (xyz):

Далее при преобразовании формул для упрощения записи мы будем опускать скобки вокруг конъюнкций.

1) Построим таблицу истинности функции по формуле (F ).

x y z			((		! (			= (y								f
				x		yz))					z	)) _ (xyz)
0	0	0	1		0	0		1	0	1		1	0			1
0	0	1	1		1	1		0	1	0		0	0			0
0	1	0	1		0	0		1	1	1		1	0			1
0	1	1	1		0	0		1	0	0		1	0			1
1	0	0	0		1	0		1	0	1		1	0			1
1	0	1	0		1	1		0	1	0		1	1			1
1	1	0	0		1	0		0	1	1		0	0			0
1	1	1	0		1	0		1	0	0		1	0			1
			3		4	1		7	6	5		8	2

2) Построим матрицу Грея функции f(x; y; z) по таблице истинности. Отметим на матрице наборы, на которых f(x; y; z)=1.

y z

x

63

3) Получим ДНФ0 по формуле (F ) разложением по переменным.

Применим к подформуле (x ! yz)=(y z) разложение Шеннона по переменной y (она встречается чаще, чем переменная x и так же часто, как переменная z).

(F ) = ((x ! yz)=(y z)) _ xyz =

= y[(x ! 1z)=(1 z)] _ y[(x ! 0z)=(0 z)] _ xyz =

[применим свойства 0 и 1 для конъюнкции ]

=y[(x ! 0)=(1 z)] _ y[(x ! z)=(0 z)] _ xyz =

[ выведем свойства 0 и 1 для импликации и эквивалентности

a	a ! 0	1 a	0 a	a ! 0 =
						a
0	1	0	1	1 a = a
1	0	1	0	0 a =
					a

èупростим выражение ]

=y[x=z] _ y[(x ! z)=z] _ xyz =

[разложим коэффициенты при y и y по переменной z ]

=y [z (x=1) _ z (x=0)] _ y [z ((x ! 1)=1) _ z ((x ! 0)=0)] _ x y z =

=y [z (x=0) _ z (x=1)] _ y [z ((x ! 1)=1) _ z ((x ! 0)=0)] _ x y z =

[ выведем свойства 0 и 1 для импликации и штриха Шеффера

a	a ! 1	a=0	a=1	a ! 1 = 1
0	1	1	1	a=0 = 1
1	1	1	0	a=1 =
					a

èупростим выражение ]

=y [z1 _ z x] _ y [z(1=1) _ z(x=0)] _ x y z =

=y [z _ z x] _ y [z0 _ z1] _ x y z =

[используем свойства 0 и 1 и закон дистрибутивности ]

=y z _ x y z _ y z _ x y z = ÄÍÔ0: K1 K2 K3 K4

64

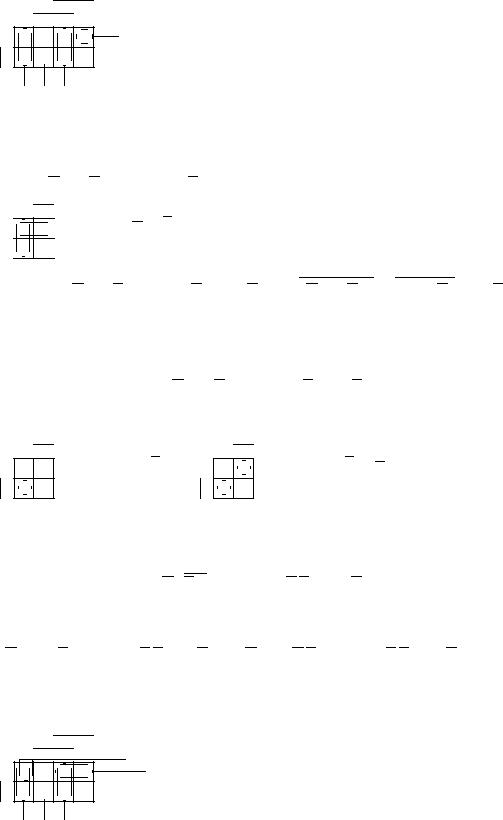
4) Построим матрицу Грея по ДНФ 0.

z	y
	-I2
x ? ? ?
I3 I4 I1

5) Получим ДНФ00 по формуле (F ) подстановкой кратчайших ДНФ элементарных функций. Заменим штрих Шеффера a=b КратДНФ при a = x ! yz, b = y z:

b a=b = a _ b a

(F ) = ((x ! yz)=(y z)) _ xyz = ((x ! yz) _ (y z)) _ xyz =

[ заменим инверсию импликации на не импликацию и инверсию эквивалентности на дизъюнкцию с исключением ]

= (x ,! yz) _ (y z) _ xyz =

[ найдем КратДНФ не импликации и дизъюнкции с исключением

		ba , b = ab		ba		b = a b	_	a b
		!
a			a

èподставим их в формулу ]

=x (y z) _ (y z _ y z) _ x y z =

[ применим законы де Моргана, дистрибутивности, ассоциативности ]

= x (y _ z) _ y z _ y z _ x y z = x y _ x z _ y z _ y z _ x y z = ÄÍÔ00: K1 K2 K3 K4 K5

40) Построим матрицу Грея по ДНФ 00.

z y I

- 2 I

- 1

x? ? ?

I4 I5 I3

65

6) Построим сокращенную ДНФ по матрице Грея . Выделим все максимальные интервалы, они зададут конъюнкции сокращенной ДНФ.

		y		СокрДНФ = y z x y y z x z x y x z:
		z	- I5
			- I6
			- I4	K1 _ K2 _ K3 _ K4 _ K5 _ K6

x? ? ?

I1 I2 I3

7)Преобразуем сокращенную ДНФ в совершенную ДНФ .

y z _ x y _ y z _ x z _ x y _ x z = x y z _ x y z _ x y z _ x y z_ _x y z _ x y z _ x y z _ x y z _ x y z _ x y z _ x y z _ x y z =

=x y z _ x y z _ x y z _ x y z _ x y z _ x y z = СовДНФ.

K1 K2 K3 K4 K5 K6

8) Построим кратчайшую ДНФ по матрице Грея . Выделим на матрице минимальное число максимальных интервалов, образующих достаточное множество, и по нему построим кратчайшую ДНФ.

	I1	z	y
	6		-I2	КратДНФ = y z	x y	_	x z:
x			-I3	K1	_ K2		K3

70) Преобразуем кратчайшую ДНФ в совершенную ДНФ .

y z _ x y _ x z = x y z _ x y z _ x y z _ x y z _ x y z _ x y z = СовДНФ: K1 K2 K5 K6 K4 K3

Здесь конъюнкциям присвоены номера из совершенной ДНФ задачи

7), сравнение показывает, что совершенные ДНФ совпали.

400) Построим матрицу Грея по совершенной ДНФ . Каждая пол-

ная конъюнкция задается точкой, которая на матрице обозначена номером конъюнкции в совершенной ДНФ.

y

z

2		5	6
1	3	4

x

Вывод. Матрицы Грея, полученные при решении задач 2), 4), 40), 400), совпадают, следовательно, ошибок при выполнении контрольной работы нет (кроме, может быть, неверной расстановки скобок).

66

11.Минимизация булевых функций.

Âпредыдущем разделе мы познакомились с различными типами ДНФ и научились их находить визуально по матрице Грея. Перейдем

êизучению формальных методов построения сокращенной, безызбыточных, минимальных и кратчайших ДНФ булевой функции.

Интерес к кратчайшим и минимальным ДНФ основан на их оптимальности (по длине и рангу соответственно), которая положительно проявляется, по крайней мере, в двух случаях. Во-первых, с оптимальными ДНФ легче оперировать, то есть вычислять значения функции, строить матрицу Грея и подставлять в другие формулы. Во-вторых, оптимальные ДНФ более удобны для построения по ним схем из логических элементов: дизъюнкторов, конъюнкторов и инверторов.

Пример. Рассмотрим мажоритарную функцию.

			z y	СовДНФf = x y z		x y z		x y z		x y z
				КратДНФf = x y	_	x z	y z		_
							_
					_ _

x

Нарисуем схемы по совершенной и кратчайшей ДНФ. Логические элементы изобразим как соответственно обозначенные прямоугольники.

^

AA

x

x

AA

tJ

^

JJ

tBZZ

^

Q

A

JJ

J

B Z

"

Q A

y

J

JJ

B

Z

"

Q

-

J

y BB

"

"Z"

ZZ

_

f

tJ

^

_

-

f

"

J

" B

tbbbB

^

z

JJ

B b

J

BB bbb

tPPP

^

B

z t

^

Схема, построенная по кратчайшей ДНФ (справа), оказалась проще: она содержит меньше логических элементов и связей.

Интерес к сокращенной ДНФ вызван тем, что она является промежуточной при построении кратчайших, минимальных и безызбыточ- ных ДНФ. Безызбыточные ДНФ интересны как сами по себе, так как часто оказываются близкими к оптимальным, так и тем, что среди них находятся все минимальные и простые кратчайшие ДНФ.

67

Определение. Минимизировать булеву функцию значит построить ее кратчайшую или минимальную ДНФ или все кратчайшие или минимальные ДНФ (постановка задачи уточняется дополнительно).

Рассмотрим двухэтапный подход к минимизации булевой функции, основанный на теоремах о кратчайшей и минимальных ДНФ (подраздел 9.2), утверждающих, что все минимальные и хотя бы одна из кратчайших ДНФ состоят из простых импликант.

Первый этап: найдем все простые импликанты функции, то есть конъюнкции ее сокращенной ДНФ.

Второй этап: из сокращенной ДНФ выделим конъюнкции искомых ДНФ (кратчайших или минимальных).

Далее наряду с языком ДНФ будем использовать язык интервалов как более наглядный при визуальном решении и более удобный при компьютерной реализации алгоритмов. Напомним аналогию между рядом понятий (относящихся к одной и той же булевой функции) на упомянутых языках.

ßçûê ÄÍÔ	Язык интервалов
полная	точка
конъюнкция-импликанта
элементарная	допустимый интервал
конъюнкция-импликанта
простая импликанта	максимальный интервал
ÄÍÔ	достаточное множество интервалов
совершенная ДНФ	множество всех точек
сокращенная ДНФ	множество всех максимальных
	интервалов
кратчайшая ДНФ	достаточное множество из
	минимального числа
	максимальных интервалов
минимальная ДНФ	достаточное множество максимальных
	интервалов с минимальной суммой
	рангов
безызбыточная ДНФ	достаточное множество максимальных
	интервалов, которое при удалении
	любого интервала перестает быть
	достаточным

68

11.1. Получение сокращенной ДНФ первый этап минимизации

Прежде всего вспомним законы поглощения и склеивания конъюнкций и добавим к ним закон неполного склеивания.

Закон поглощения:	K1 _ K1K2 = K1.
Закон склеивания:	xK _
		xK = K.
Закон неполного склеивания :	xK _
		xK = xK _ xK _ K.

Закон обобщенного склеивания : xK1 _ xK2 = xK1 _ xK2 _ K1K2:

Очевидно, что закон неполного склеивания следует из закона обобщенного склеивания (при K1 = K2 = K), а закон склеивания из закона неполного склеивания (если в последнем выполнить поглощения конъюнкций). Переведем эти законы на язык интервалов, используя интервалы и представляющие их троичные векторы как синонимы.

Закон поглощения говорит о том, что если объединение двух ин- тервалов I и I0 совпадает с I, то интервал I0 содержится в интервале

I (поглощается им). Значит, поглощаемый вектор должен получаться

из поглощающего заменой некоторых его внутренних компонент ( ) на внешние (0 или 1).

= 1 0

Пример. В паре троичных векторов = 0 1 0 1 вектор погло- щается вектором .

Закон склеивания объединяет два соседних интервала в один. Напомним, что соседние интервалы совпадают по номерам внешних компонент, но различаются по значению ровно одной из них (ортогональной). При склеивании получается интервал, который отличается от исходных лишь в ортогональной компоненте она становится внутренней (эта операция уже рассматривалась в подразделе 2.2.3).

Пример. Результатом склеивания соседних векторов и является вектор :

= 0 0 1 ;

= 0 1 1 ;

= 0 1 :

Закон неполного склеивания объединяет два соседних интервала и добавляет к результату исходные интервалы.

Пример. Результатом неполного склеивания векторов и из предыдущего примера являются три вектора: , и .

69

Закон обобщенного склеивания объединяет соседние части двух смежных интервалов. Смежные интервалы могут не совпадать по номерам внешних компонент, но должны быть ортогональны ровно по одной из них. Результатом обобщенного склеивания являются три интервала: два исходных и третий, который строится так:

компоненты, по которым исходные векторы совпадают, сохраняют свои значения;

компоненты, которые в одном из векторов являются внешними,

àв другом внутренними, принимают значения внешних компонент;

ортогональная компонента становится внутренней.

Пример. Результатом обобщенного склеивания смежных векторов

и являются векторы , и :

= 0 0 1 0 1 ;

= 1 0 1 0 1 ;

= 0 1 0 0 1 1 :

11.1.1.Теорема Квайна и алгоритм Квайна МакКласки

Первый метод построения сокращенной ДНФ булевой функции основан на следующей теореме.

Теорема (Квайна). Чтобы получить сокращенную ДНФ булевой функции из ее совершенной ДНФ, надо выполнить всевозможные неполные склеивания соседних конъюнкций, а затем всевозможные поглощения конъюнкций.

Опираясь на теорему Квайна, МакКласки сформулировал алгоритм, который организует построение сокращенной ДНФ более эффективно, чем это предложено в теореме. Рассмотрим предложения МакКласки.

Во-первых, конъюнкции в алгоритме представляются булевыми и троичными векторами, что делает вычисления более простыми и более приспособленными для компьютерной реализации.

Во-вторых, соседние векторы отличаются по весу (числу единич- ных компонент) ровно на единицу. Поэтому в алгоритме не проверяются на возможность склеивания векторы, чьи веса равны или отли- чаются более чем на единицу.

70