27.​ Векторы на прямой, на плоскости, в пространстве. Геометрический смысл линейной зависимости.

Утв. 1. На прямой (на плоскости, в пространстве) существует нулевой вектор (соответственно 2 неколлиниарных и 3 некомпланарных вектора). 

Утв.2. На прямой ( на плоскости, в пр-ве) всякий вектор линейно выражается через любой ненулевой вектор (соотв.любые 2 неколлиниарных и любые 3 некомпанарных вектора).

Теорема. Два вектора линейно зависимы тогда и только тогда, когда они коллиниарны.

Следствие 1. Любые два (значит, и более) вектора прямой линейно зависимы.

Теорема. Три вектора линейно зависимы тогда и только тогда, когда они компланарны.

Следствие 2. Любые три (значит, и более) вектора плоскости линейно зависимы.

Теорема. Любые четыре вектора линейно зависимы.

Вектор - математический объект, характеризующийся величиной и направлением.

Линейное пространство - множество элементов, наз. векторами, над кот. определённым образом определены операции сложения и умножения на число. В любом линейном пространстве можно выделить особую систему векторов, называемых базисом линейного пространства. Кол-во векторов в базисе равно размерности пространства. Любой вектор из пространства можно представить, как линейную комбинацию базисных векторов. То есть, если у нас есть базис , то , где - поле, над кот. опред. линейное пространство .

Выбор базиса в линейном пространстве неоднозначен, однако коэффициенты векторов при измерении базиса связанны определённым образом. Пусть есть базис и . Причём: . Матрица , полученная из коэффициентов наз. матрицей перехода от базиса к базису  и связывает координаты вектора в различных базисах следующем образом: . Связь между матрицами перехода между двумя базисами: . Векторы могут иметь различную природу: направленные отрезки, матрицы, числа, ф-ции и др., однако все линейные пространства 1ой размерности изоморфны между собой.

Операции над векторами

Пусть в линейном пространстве выбран базис и в нём представлены вектора , , тогда суммой векторов будет называется следующий вектор: . Пусть есть число , тогда произведением вектора на число будет называться следующий вектор:  Два ненулевых вектора и называются коллинеарными, если .

Ф-ция (в другом обозначении), ставящая любым двум векторамв соответствие число и удовлетворяющая следующим аксиомам:

Линейность по первому аргументу: 

Эрмитова симметричность: (в случае если векторы определены над полем действительных чисел, то)

Положительная определённость: тогда и только тогда, когда, называетсяскалярным произведением вектора на вектор. Конечномерное линейное пространство с введённым скалярным произведением называетсяевклидовым. Для пр-тв над полем комплексных чисел иногда применяют термин унитарное пространство.

Два ненулевых вектора называютсяортогональными, если . Базисевклидова пространства называетсяортогональным, если . Базис называетсяортонормированным, если , где-символ Кронекера.

Скалярное произведение является билинейной формой, поэтому его можно записать в следующем виде: , где-матрица Грамма. В случае ортонормированного базиса матрица будет единичной => если  ,,тов случае действительного пространства ив случае комплексного.

Так же в линейном пр-ве можно ввести понятие нормы. Это ф-ция, ставящая в соответствие любому вектору лин. пр-ва неотрицательное вещественное число и удовлетворяющая следующим аксиомам:тогда и только тогда, когда.

.

.

Угол между векторамиопределяется, как.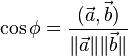

Линейное (векторное пр-во) надполем - упорядоченная четвёрка, где

 - непустое мн-во элементов произвольной природы, векторы;- поле, элементы кот. наз.скалярами;

 — операция сложения векторов, сопоставляющая каждой паре элементов множестваединственный элемент множества, обозначаемый;

 — операция умножения векторов на скаляры, сопоставляющая каждому эл-ту поляи каждому эл-тумножестваединственный элемент множества, обозначаемый;

причём, заданные операции удовлетворяют следующим аксиомам линейного (векторного) пространства:

, для любых (коммутативность сложения);

существует такой элемент , чтодля любого(существование нейтрального элемента относительно сложения), в частности не пусто;

для любого сущ-т такой элемент, что(существование противоположного элемента относительно сложения).

 (ассоциативность умножения на скаляр);

 (унитарность: умножение на нейтральный (по умножению) элемент поля F сохраняет вектор).

 (дистрибутивность умножения на вектор относительно сложения скаляров);

(дистрибутивность умножения на скаляр относительно сложения векторов).

В 3хмерном пространстве понятие «длина вектора» понимаетсямкак расстояние между его началом и концом. Наиболее важными свойствами «длины вектора» являются следующие:

Длина нуль-вектора, , равна нулю; длина любого другого вектора положительна.

Умножение вектора на положительное число во столько же раз увеличивает длину вектора.

Действует неравенство треугольника.

Обобщение этих свойств на более абстрактные векторные пространства носит название нормы. Векторное пространство, в котором определена норма, называется нормированным пространством.

Простейшие свойства

Векторное пространство является абелевой группой (коммутативной) по сложению.

Нейтральный элемент является единственным, что вытекает из групповых св-в.

 для любого .

Для любого противоположный элементявляется единственным.

 для любого .

 для любых и.

 для любого .