1. Система линейных уравнений. Элементарные преобразования систем. Эквивалентность систем. Система m линейных уравнений  с  n  неизвестными — это система уравнений вида 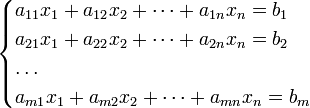. Элементарные преобразования: перестановка строк, умножение строки на ненулевое число и к одному уравнению прибавить другое, умноженное на число. Эквивалентность систем – выражение одной системы через другую. В результате элементарных преобразований сохраняется эквивалентность матриц.

2. Однородные и неоднородные системы. Свойства их множества. Системы, в которых свободные члены всех уравнений равны нулю называются однородными. В противном случае – неоднородные. Свойства их множества решений:

• любая линейная комбинация решений однородной системы является решением той же системы;

• общее решение совместной неоднородной системы линейных уравнений можно представить как сумму частного решения этой неоднородной системы и общего решения соответствующей однородной системы;

• общее решение неопределенной однородной системы представляется в виде линейной комбинации некоторой линейной независимой системы ее решений;

• любая однородная системы является совместной;

• разность двух решений неоднородной системы оказывается решением соответствующей однородной системы.

3. Приведение матриц элементарными преобразованиями строк к ступенчатому виду. Матрица называется ступенчатой, если первый ненулевой элемент каждой очередной строки стоит правее первого ненулевого элемента предыдущей строки. С помощью элементарных преобразований любую матрицу можно привести к ступенчатому виду. Необходимые условия ступенчатого вида:

• ниже нулевой строки стоят нулевые строки;

• в ненулевой строки первый ненулевой элемент равен единице;

• в последующей строке первый ненулевой элемент стоит правее, чем в предыдущей строке;

• над и под единицами стоят нули.

4. Решение систем линейных уравнений методом Гаусса.

Решая методом Гаусса, необходимо записать систему уравнений в матричном виде, привести нашу расширенную матрицу к ступенчатому виду. Затем необходимо исследовать полученную ступенчатую матрицу, тут у нас идет разделение на три пункта:

• Если она имеет строку вида (0…0|b) при b=/0, то данная система несовместна;

• Если число строк нашей ступенчатой матрицы меньше числа неизвестных, то выбираем главные неизвестные (первые ненулевые элементы строк ступенчатой матрицы) и свободные неизвестные и через последние выражаем главные;

• Когда число ненулевых строк нашей ступенчатой матрицы равно числу неизвестных, то система – определенная.

5. Фундаментальная система решений однородной системы линейных уравнений.

Фундаментальной системой решений однородной системы линейных уравнений называется база множества всех решений этой системы. Число решений в фундаментальной системе решений однородной линейной системы из m уравнений от n переменных равно n-r, где r — ранг матрицы системы.

6. Операции над матрицами (сложение, умножение на число, произведение, транспонирование)

Суммой матриц А и В одинакового размера называется матрица С того же размера, каждый элемент которой равен сумме соответствующих элементов матриц А и В.Умножить матрицу на число означает умножить каждый элемент этой матрицы на данное число. С-ва сложения матриц и умножения их на число: даны матрицы А, В и С и числа h и u. Тогда верны следующие равенства: 1) А+В=В+А; 2) (А+В)+С=А+(В+С); 3) h(А+В)=hА+hВ; 4) (h+u)А=hА+uА; 5) (hu)А= (hА)u; 6) А+(-А)=0. Матрица B называется транспонированной к матрице А, если строки матрицы B являются столбцами матрицы А с сохранением их порядка. Свойства: (А^T)^T=A; (А+В)^T=A^T+B^T. Произведением матриц А размера m*n и матриц В размера n*k называется матрица С размера m*k , каждый элемент которой равен скалярному произведению вектора-строки А(маленькая)i на вектор-столбец В(маленькая)j. АВ не равно ВА.

7. Индуктивное определение определителя. Определители второго и третьего порядков.

Индуктивное определение определителя: detA n=1, тогда |a11|= det(a11)= a11. или сделаем разложение по строке или столбцу.

8. Изменение определителя при элементарных преобразованиях строк. Вычисление треугольного определителя.

Если в квадратной матрице А к одной строке прибавить другую, умноженную на число, то ее определитель не меняется. Если строку матрицы умножить на число, то ее определитель умножается на это число. Если в определители две строки поменять местами, то определитель изменит знак. Треугольная матрица — квадратная матрица, в которой все элементы ниже или выше главной диагонали равны нулю. Определитель треугольной матрицы равен произведению элементов на её главной диагонали .

9. Определитель произведения матриц. Определитель транспонированной матрицы. Определитель матрицы с углом нулей.

Определитель произведения квадратных матриц одинакового порядка равен произведению их определителей, т.е. |A*B|=|A|*|B|. При транспонировании определитель не меняется. Определитель матрицы с углом нулей: пусть матрица разбита на блоки |А В 0 С|, где А и С- квадратные, тогда определитель всей матрицы равен |А|*|С|.