5

Министерство транспорта Российской Федерации

ЕНИСЕЙСКИЙ ФИЛИАЛ ФГОУ ВПО

Новосибирская государственная академия водного транспорта

Т.И. Лелеков

Теоретическая механика

Методические указания и контрольные задания для студентов специальностей:

180105 − “Техническая эксплуатация судов и судового оборудования”

140604 − “Электропривод и автоматика промышленных установок и технологических комплексов”

180402 − “Судовождение на ВВП и прибрежном плавании”

Красноярск 2009

Министерство транспорта Российской Федерации

ЕНИСЕЙСКИЙ ФИЛИАЛ ФГОУ ВПО

Новосибирская государственная академия водного транспорта

Т.И. Лелеков

Теоретическая механика

Методические указания и контрольные задания для студентов специальностей:

180105 − “Техническая эксплуатация судов и судового оборудования”

140604 − “Электропривод и автоматика промышленных установок и технологических комплексов”

Красноярск 2009

УДК 531.8

Т 33

Лелеков Т.И. Теоретическая механика. Методические указания и контрольные задания для студентов. − Красноярск, Красноярский филиал ФГОУ ВПО НГАВТ, 2009. – 36 с.

Методические указания разработаны в соответствии с Государственным образовательным стандартом высшего профессионального образования по подготовки студентов специальностей инженеров водного транспорта. Излагается содержание лекционных, практических занятий, контрольные задания, приводятся варианты решения задач.

Печатается по решению редакционно-издательского совета Енисейского филиала ФГОУ ВПО НГАВТ

© Енисейский филиал ФГОУ ВПО Новосибирская государственная академия водного транспорта

ВВЕДЕНИЕ

Теоретическая механика как одна из важнейших физико-математических дисциплин играет существенную роль в подготовке инженеров водного транспорта.

На основных законах и принципах теоретической механики базируются многие общеинженерные дисциплины, такие, как сопротивление материалов, прикладная механика, гидравлика, теория механизмов и машин, детали машин и др.

В различных курсах по техническим специальностям подготовки инженеров водного транспорта широко используются положения теоретической механики. На основе теорем и принципов теоретической механики решаются многие инженерные задачи и осуществляется проектирование новых машин, конструкций и сооружений.

Хорошее усвоение курса теоретической механики требует не только глубокого изучения теории, но и приобретения твердых навыков в решении задач. Для этого необходимо самостоятельно решить определенное количество задач по разделам курса.

СОДЕРЖАНИЕ КУРСА

Механическое движение как одна из форм движения материи. Предмет механики. Теоретическая механика и ее место среди естественных и технических наук. Механика как теоретическая база ряда областей современной техники. Объективный характер законов механики. Основ­ные исторические этапы развития механики. Связь механики с общественным производством и ее роль в решении народнохозяйственных задач.

СТАТИКА

Основные понятия и аксиомы статики. Предмет статики. Основные понятия статики: абсолютно твердое тело, сила, эквивалентные и уравновешенные системы сил, равнодействующая, силы внешние и внутренние.

Аксиомы статики. Связи и реакции связей. Основные виды связей: гладкая плоскость или поверхность, гладкая опора, гибкая нить, цилиндрический и сферический шарниры, невесомый стержень; реакции этих связей.

Система сходящихся сил. Геометрический и аналитический способы сложения сил. Сходящиеся силы. Равнодействующая сходящихся сил. Геометрическое и аналитические условия равновесия системы сходящихся сил.

Равновесие произвольной системы сил. Момент силы относительно точки (центра) как вектор. Пара сил; момент пары. Свойства пары сил. Понятие о приведении системы сил к заданному центру. Главный вектор и главный момент системы сил. Условия равновесия произвольной системы сил, приложенных к твердому телу.

Система сил, расположенных на плоскости (плоская система сил). Алгебраическая величина момента силы. (Вычисление главного вектора и главного момента плоской системы сил.) Аналитические условия равновесия плоской системы сил. Условия равновесия плоской системы параллельных сил. Теорема Вариньона о моменте равнодействующей. (Равновесие системы тел.)

Система сил, расположенных в пространстве (пространственная система сил). Момент силы относительно оси. Зависимость между моментами силы относительно центра и относительно оси, проходящей через этот центр. (Аналитические формулы для вычисления моментов силы относительно трех координатных осей. Вычисление главного вектора и главного момента пространственной системы сил.) Аналитические условия равновесия произвольной пространственной системы сил. Условия равновесия пространственной системы параллельных сил.

Центр тяжести. Центр тяжести твердого тела и его координаты. Центр тяжести объема, площади и линии. Способы определения положения центров тяжести.

КИНЕМАТИКА

Введение в кинематику. Предмет кинематики. Пространство и время в классической механике. Относительность механического движения. Система отсчета. Задачи кинематики.

Кинематика точки. Векторный способ задания движения точки. Траектория точки. Скорость точки как производная от ее радиуса−вектора по времени. Ускорение точки как производная от вектора скорости по времени. Координатный способ задания движения точки в прямоугольных декартовых координатах. Определение траектории точки. Определе­ние скорости и ускорения точки по их проекциям на координатные оси.

Естественный способ задания движения точки. Оси естественного трехгранника. Алгебраическая величина скорости точки. Определение ускорения точки по его проекциям на оси естественного трехгранника: касательное и нормальное ускорения точки.

Поступательное и вращательное движения твердого тела. Поступательное движение твердого тела. Теорема о траекториях, скоростях и ускорениях точек твердого тела при поступательном движении. Вращение твердого тела вокруг неподвижной оси. Уравнение (закон) вращательного движения твердого тела. Угловая скорость и угловое ускорение тела. Скорость и ускорение точки твердого тела, вращающегося вокруг неподвижной оси. Вектор угловой скорости тела. (Выражение скорости точки вращающегося тела в виде векторного произведения.)

Плоскопараллельное (плоское) движение твердого тела. Плоское движение твердого тела и движение плоской фигуры в ее плоскости. Уравнения движения плоской фигуры. Разложение движения плоской фигуры на поступательное вместе с полюсом и вращательное вокруг по­люса: независимость угловой скорости фигуры от выбора полюса. Опре­деление скорости любой точки фигуры как геометрической суммы скорости полюса и скорости этой точки при вращении фигуры вокруг полюса. Теорема о проекциях скоростей двух точек фигуры (тела). Мгновенный центр скоростей. Определение скоростей точек плоской фигуры с помощью мгновенного центра скоростей.

Сложное (составное) движение точки. Абсолютное и относительное движения точки; переносное движение. Теорема о сложении скоростей. Теорема о сложении ускорений при переносном поступательном и переносном вращательном движениях; кориолисово ускорение и его вычисление.

ДИНАМИКА

Введение в динамику. Предмет динамики. Основные понятия и определения: масса, материальная точка, сила. Законы механики Галилея-Ньютона. Инерциальная система отсчета. Задачи динамики.

Динамика точки. Дифференциальные уравнения движения свободной и несвободной материальной точки в декартовых координатах. (Уравнения движения материальной точки в проекциях на оси естественного трехгранника.) Две основные задачи динамики для материальной точки. Решение первой задачи динамики.

Решение второй задачи динамики. Начальные условия. Постоянные интегрирования и их определение по начальным условиям. Примеры интегрирования дифференциальных уравнений движения точки в случаях силы, зависящей от времени, от положения точки и от ее скорости.

Относительное движение материальной точки. Дифференциальные уравнения относительного движения материальной точки; переносная и кориолисова силы инерции. Принцип относительности классической механики. Случай относительного покоя.

Прямолинейные колебания точки. Свободные колебания материальной точки под действием восстанавливающей силы, пропорциональной расстоянию от центра колебаний. Амплитуда, начальная фаза, частота и период колебаний. Затухающие колебания материальной точки при сопротивлении, пропорциональном скорости; период этих колебаний, декремент колебаний. Вынужденные колебания точки при гармоничес­кой возмущающей силе и сопротивлении, пропорциональном скорости. Резонанс.

Введение в динамику механической системы. Механическая система. Классификация сил, действующих на систему: силы активные (задаваемые) и реакции связей; силы внешние и внутренние. Свойства внутренних сил. Масса системы. Центр масс; радиус-вектор и координаты центра масс.

Момент инерции. Момент инерции твердого тела относительно оси; радиус инерции. Теорема о моментах инерции тела относительно параллельных осей. Примеры вычисления моментов инерции: моменты инерции однородного тонкого стержня, тонкого круглого кольца или полого цилиндра, круглого диска или сплошного круглого цилиндра.

Теорема о движении центра масс. Дифференциальные уравнения движения механической системы. Теорема о движении центра масс механической системы. Закон сохранения движения центра масс.

Теорема об изменении количества движения. Количество движения материальной точки. Элементарный импульс силы. Импульс силы за конечный промежуток времени. Теорема об изменении количества движения точки в дифференциальной и в конечной формах.

Количество движения механической системы; его выражение через массу системы и скорость ее центра масс. Теорема об изменении количества движения механической системы в дифференциальной и в конечной формах. Закон сохранения количества движения механической системы.

Теорема об изменении момента количества движения. Момент количества движения материальной точки относительно центра и относительно оси. Теорема об изменении момента количества движения точки. (Сохранение момента количества движения точки в случае центральной силы; закон площадей.)

Главный момент количеств движения или кинетический момент механической системы относительно центра и относительно оси. Кинетический момент вращающегося твердого тела относительно оси вращения. Теорема об изменении кинетического момента механической системы. Закон сохранения кинетического момента механической системы. (Дифференциальное уравнение вращательного движения твердого тела вокруг неподвижной оси.)

Теорема об изменении кинетической энергии. Кинетическая энергия материальной точки. Элементарная работа силы; аналитическое выражение элементарной работы. Работа силы на конечном перемещении точки ее приложения. Работа силы тяжести, силы упругости и силы тяготения. Мощность. Теорема об изменении кинетической энергии точки.

Кинетическая энергия механической системы. Кинетическая энергия твердого тела при поступательном движении, при вращении вокруг неподвижной оси и при плоскопараллельном движении тела. Теорема об изменении кинетической энергии механической системы. Равенство нулю суммы работ внутренних сил в твердом теле. Работа и мощность сил, приложенных к твердому телу, вращающемуся вокруг неподвижной оси.

Принцип Даламбера. Принцип возможных перемещений. Сила инерции материальной точки. Принцип Даламбера для материальной точки и механической системы. (Возможные или виртуальные перемещения точки и механической системы. Число степеней свободы системы. Идеальные связи. Принцип возможных перемещений. Общее уравнение динамики.)

Уравнения Лагранжа. Обобщенные координаты системы; обобщенные скорости. Выражение элементарной работы в обобщенных координатах. Обобщенные силы и их вычисление. Дифференциальные уравнения движения системы в обобщенных координатах или уравнения Лагранжа 2-го рода.

СПИСОК ЛИТЕРАТУРЫ

1. Тарг С.М. Краткий курс теоретической механики. −М.: Высшая школа, 1995 − 415 с.

2. Гордеев О.И., Дегтярева В.В., Ратничкин А.А., Ройтман АЛ. и др. Введение в курс теоретической механики. Новосибирск: Наука, 1992-144 с.

3. Яблонский А.А. Сборник заданий для курсовых работ по теоретической механике, −М.: Высшая школа. 2001. − 3бб с.

4. Мещерский И.В. Сборник задач по теоретической механике. − М.: Наука, 1998. − 448 с.

5. Кепе О.Э. Сборник коротких задач по теоретической механике. −М.: Высшая школа. 1989. −368 с.

ЗАДАНИЕ 1

РАСЧЕТ СТАТИЧЕСКИХ НАГРУЗОК НА КОНСТРУКЦИИ

1. ОПРЕДЕЛЕНИЕ РЕАКЦИИ ОПОР И ЗАДЕЛКИ КОНСОЛЬНОЙ БАЛКИ

Для заданных систем балок рис. 1.1 требуется определить реакции опор и заделки, а также написать выражения Q и M для каждого участка в общем виде, построить эпюры Q и M, найти M_max. Данные величин размеров, действующих сил и моментов выбрать по табл. 1.1.

Рис. 1.1

Таблица 1

N строки	Схема по рис. 1	L1, м	L2, м	a1/a	a2/a	a3/a	M, кН·м	P, кН	q, кН/м
1	I	1,1	6	1	9	1	10	10	10
2	II	1,2	7	2	8	2	20	20	20
3	III	1,3	3	3	7	3	3	3	3
4	IV	1,4	4	4	6	4	4	4	4
5	V	1,5	5	5	5	5	5	5	5
6	VI	1,6	6	6	6	1	6	6	6
7	VII	1,7	7	7	7	2	7	7	7
8	VIII	1,8	8	8	8	3	8	8	8
9	IX	1,9	9	9	9	4	9	9	9
0	X	2,0	10	10	10	5	10	10	10
	e	d	e	e	d	e	e	d	e

Пример. Горизонтальная балка АВ длиной L = 1,2 м, поддерживающая балкон, заделана в стену. На балку действует равномерно распределенная нагрузка интенсивности q = 1,25 кН/м. Определить реакции заделки (рис. 1.2).

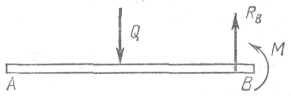
Рис. 1.2

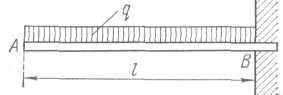
Рис. 1.3

Решение. Рассматриваем равновесие сил, приложенных к балке АВ. Равномерно распределенную нагрузку можно заменить сосредоточенной силой Q - равнодействующей системы равных парал­лельных сил, приложенной в середине загруженного участка АВ. Модуль этой силы

Q = qL= 1,25 кН/м · 1,2 м = 1,5 кН

Реакции заделки представляют собой силы, распределенные по всей опорной пло­щади, причем на нижнюю поверхность балки действуют силы, направленные вверх, а на верхнюю — силы, направленные вниз. Из этой системы сил образуется вер­тикальная реакция опоры (если все заданные силы вертикальны) и реактивная пара сил, препятствующая вращению балки вокруг закрепленного конца. Момент этой пары сил называется опорным моментом. Показываем на схеме (рис. 1.3) реакцию заделки R_B и реактивную пару с моментом М. Условимся направ­лять реакцию опоры вверх, а реактивную пару — в сторону, противоположную вра­щению часовой стрелки. Истинное их направление определим по знаку ответа. Составляем два уравнения равновесия параллельных сил на плоскости. При этом сумму моментов всех сил составляем относительно точки В, так как в этой точке приложена неизвестная реакция опоры R_B. Сумму моментов сил реактивной пары относительно точки В включаем в уравнение в виде момента пары М:

∑М_iB = 0; Q(AB/2) + M = 0;

M = - Q(AB/2) = - 1,5 · 0,6 = - 0,9 кН·м.

Момент получен со знаком минус, следовательно, реактивная пара сил имеет направление, противоположное принятому на расчетной схеме, т. е. пара направлена в сторону вращения часовой стрелки

∑±Р_i = 0; − Q + R_B = 0; R_B = Q = 1,5 кН.

Знак плюс показывает, что реакция R_B направлена так как принято на расчетной схеме, т. е. вверх.

Пример. Определить реакции опор консольной балки АВ весом G = 15 кН, находящейся под действием сил Р₁ = 40 кН, Р₂ = 30 кН, и пары с моментом М = 30кН·м. Известны размеры: АВ = 9 м; АС= 1,5 м; CD = бм; СЕ = 2 м (рис. 1.4).

Решение. Рассматрим равновесие плоской системы сил, действующей на балку АВ. Покажим действующие на балку заданные силы: Р₁, Р₂, пару сил М, а также вес балки G, который прикладываем в середине О длины АВ, считая балку однородной (рис. 1.5).

Мысленно отбрасываем связи: шарнирно-неподвижную опору С и опору на катках D, заменяя их действие соответствующими реакциями. Реакция опоры R_D направлена перпендикулярно к опорной плоскости, т. е. вертикально. Линия дей­ствия реакции опоры С не известна. Если на рассматриваемое тело действуют силы, произвольно расположенные на плоскости, то необходимо провести оси координат и разложить реакцию неизвестного направления на две составляющие, направленные вдоль осей координат. Оси могут иметь любое направление, выбор их направления обусловлен характером задачи, В рассматриваемой задаче направляем ось х вдоль горизонтальной оси балки вправо, а ось y — вертикально вверх. Направления составляющих Х_C и Y_C реакции опоры С принимаем совпадающими с направлениями осей координат. В случае, когда принятое направление не совпадает с действитель­ным, ответ, полученный для соответствующей силы при решении задачи, имеет знак минус.

Для плоской системы сил P₁ Р₂, G, Х_C, Y_C, R_D и пары сил с моментом М, действующих на балку, составляем три уравнения равновесия:

∑ M_iС = 0; ∑ X_i = 0; ∑ Y_i =0.

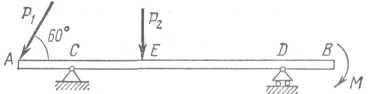
Рис. 1.4

Из трех уравнений можно найти три неизвестные величины Х_C, Y_C, R_D. Необходимо помнить, что до составления уравнений равновесия сил на расчетной схеме должны быть показаны все силы, действующие на рассматриваемое тело как известные, так и неизве­стные (рис. 1.5). При составлении первого уравнения за центр моментов принимается, как правило, точка, относительно которой моменты наибольшего числа неизвестных сил равны нулю, т. е. в данной за­даче точка С, в которой приложены две неизвестные силы Х_с и Y_c.

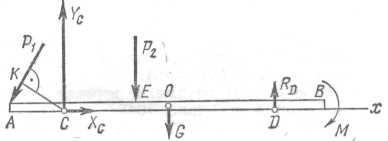
Рис. 1.5

Составим уравнения равновесия сил:

∑ M_iC = 0; P₁ · CK – G · CO + R_D · CD − |M| = 0; (1.1)

∑ X_i = 0; −P₁ cos 60° + X_C = 0; (1.2)

∑ Y_i = 0; −P₁ cos 30° + Y_C – P₂ − G + R_D = 0; (1.3)

Здесь СК — перпендикуляр, опущенный из центра моментов С на линию дей­ствия силы Р₁ длина которого равна плечу силы Р₁ относительно С,

СK = AC sin 60° = 1,5 · 0,866 = 1,3 м.

Из трех уравнений равновесия сил определяем искомые реакции. Так как неизвестные силы Х_С и Y_С не имеют момента относительно точки С, то из уравнения (1.1) определяется R_D:

R_D = (−P₁ · CK + P₂ · CE + G · CO + |M| ) / CD =

= (−40 · 1,3 + 30 · 2 + 15 · 3 + 30) / 6 = 83 / 6 = 13,8 кН.

Из уравнения (1.2)

X_С = P cos 60° = 40 · 0,5 = 20 кН.

Из уравнения (1.3)

Y_С = P₁ cos 60° + P₂ + G − R_D = 40 · 0,866 + 30 +15 − 13,8 = 65,8 кН.

Все три ответа имеют знак плюс, следовательно, принятые направления сил Х_С, Y_С и R_D совпадают с действительными.

Найдем модуль и направление реакции опоры С (рис. 1.5):

R_C = (X²_C + Y²_C)^½ = (20² + 65,8²)^½ = 68,8 кН.

2. ОПОРНЫЕ РЕАКЦИИ КОНСТРУКЦИЙ

Определить опорные реакции рамы (рис. 2.1) при действии заданной нагрузки: М = 20 кН-м; F = 10 кН; G = 10 кН; q = 5 кН/м. Размеры приведены в метрах. Весом рамы и ни­тей пренебречь. Нити считать гибкими нерастяжимыми, блоки идеальными.

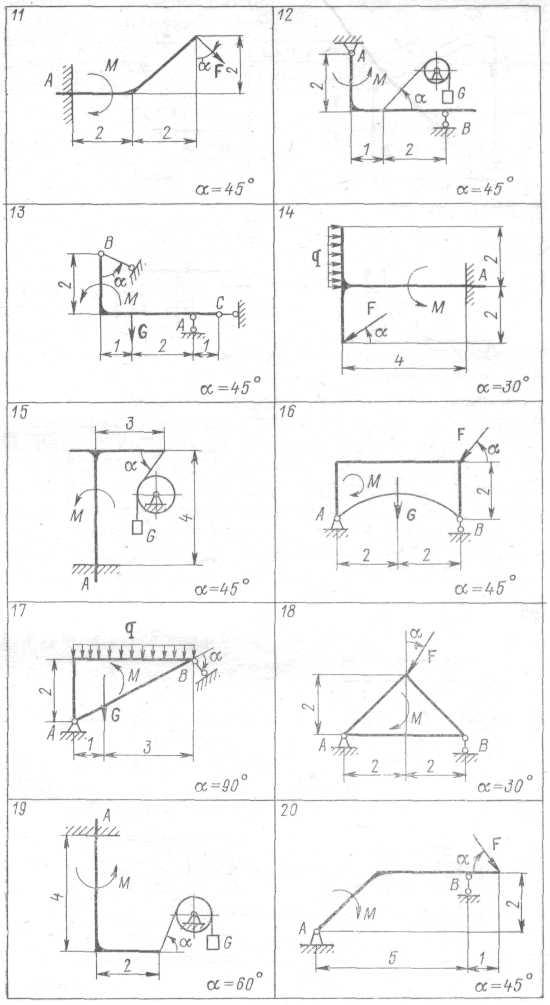
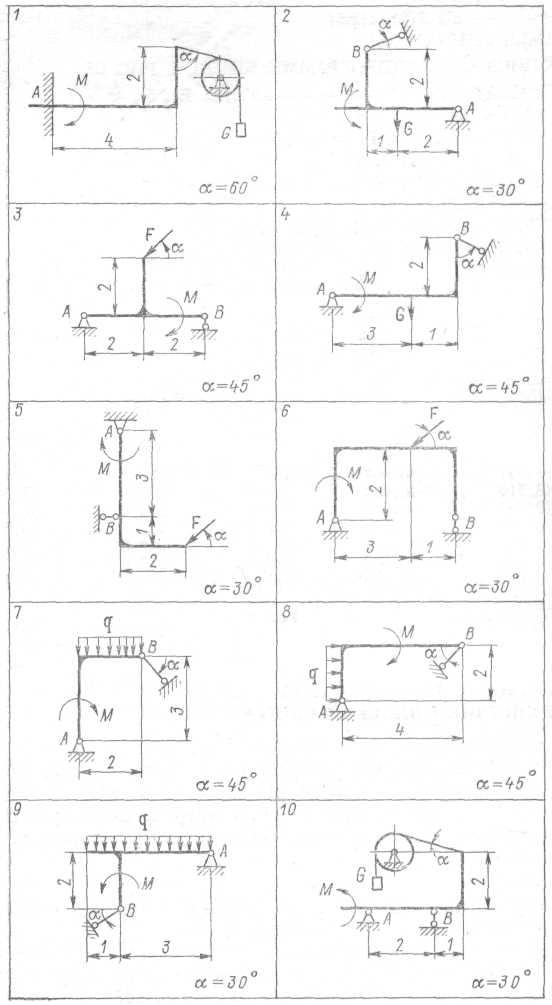
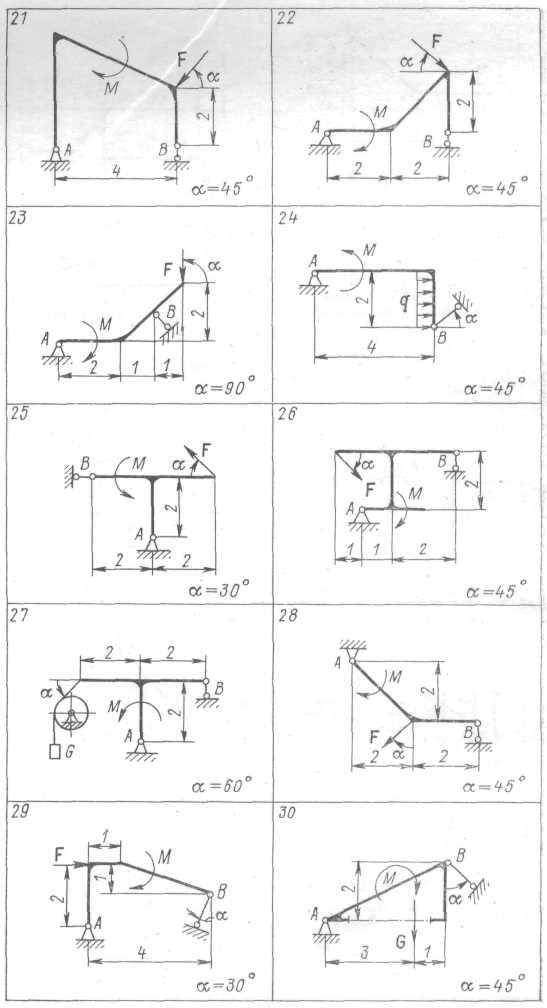
Рис. 2.1

Указание:

Задача относится к теме равновесия твердого тела под действием плоской системе сил. Для ее решения необходимо: составить уравнения равновесия и найти неизвестные реакции связей при заданном угле α; вычислить значения реакций М_А(α) или Rв(α) при изменении угла α от 0 до 360° и построить графики указанных зависимостей. Найти также наибольшее и наименьшее значения реакций М_А или R_B по модулю.

Пример. Определить реакции заделки изогнутой рамы, изображенной на рис. 2.2, а и находящейся под действием сосредоточенной силы F = 10 кН, пары сил с моментом М = 20 кН·м и равномерно распределенной нагрузки интенсивности q = 5 кН/м. Построить зависимость реакции и момента заделки от угла α при его изменении в пределах от 0 до 360° и найти наибольшее и наименьшее значения указанных реакций по модулю.

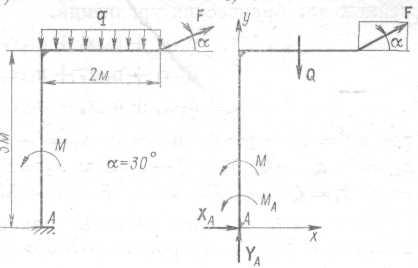
Рис. 2.2

Решение. Рассмотрим равновесие балки (рис. 2.2). Заме­ним равномерно распределенную нагрузку ее равнодействую­щей Q, равной по модулю площади эпюры распределенной на­грузки Q = 2q = 10 кН, проходящей через центр тяжести пло­щади эпюры и направленной вертикально вниз. Мысленно освободим балку от связи — жесткой заделки в точке А и за­меним ее действие реакциями Х_А, Y_A, М_А. Заданные силы и не­известные реакции связей образуют плоскую систему сил.

Уравнения равновесия твердого тела, к которому прило­жена плоская система сил, имеют вид

∑F_kx = X_A + F cos α = 0;

∑F_ky = Y_A + F sin α - Q = 0;

∑M_A(F_k) = M_A + M – Q·1 +2 F sin α - 3F cos α = 0;

Решая уравнения, получим

Х_А = - F cos α;

Y_A = Q – F sin α;

М_А = Q·1 + 3F cos α - 2F sin а - М.

Модуль реакции R_A определяется выражением

R_A = (X²_a+Y²_a)^½.

При α = 30° имеем

Х_А = - 8,66 кН; Y_A = 5 кН; М_А = 5,98 кН·м; R_A = 10 кН.

Результаты вычислений по приведенным выше формулам следующие:

α,". . . . . . . . . . . . . . .0 30

Х_А, кН. . . . . . . . . - 10 - 8,66

Y_A, кН. . . . . . . . . . 10 5

М_A, кН·м. . . . . . . . 20 5,98

Зависимости R_A (α) и М_А(α) представлены на рис. 2.3, а, б.

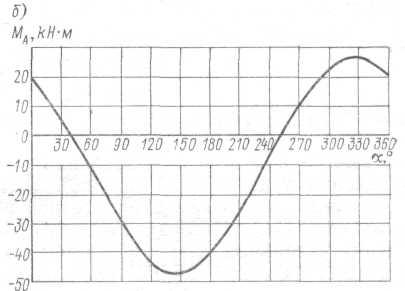
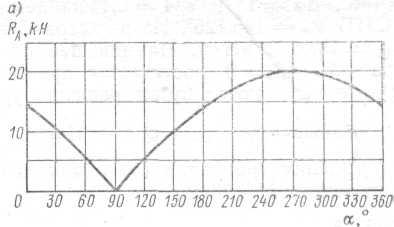
Рис. 2.3

Наибольшее и наименьшее значения величин R_A (α) и М_А(α) по модулю определяются графически из рис. 2.3.

Наибольшее значение R_A (α) = 20 кН при α = 270°, наименьшее — R_A (α) = 0 при α = 90°.

Максимальное значение момента в заделке М_А(α) = 46 кН·м при α = 145°, наименьшее значение М_А(α) = 0 при α = 40°.

3. ОПРЕДЕЛЕНИЕ УСИЛИЙ В СТЕРЖНЯХ ПЛОСКОЙ ФЕРМЫ

Определить способом сечений усилия в стержнях 1 - 3 плоской статически определимой фермы (рис. 3.1), к которой приложена сила F = 20 кН, наклоненная под углом α = 30° к горизонту. Рассчитать значения усилий S₁, S₂ и S₃ при изменении угла α от 0 до 90° и построить графики указанных зависимостей. Найти также наибольшие и наименьшие значения указанных усилий в стержнях фермы по модулю.

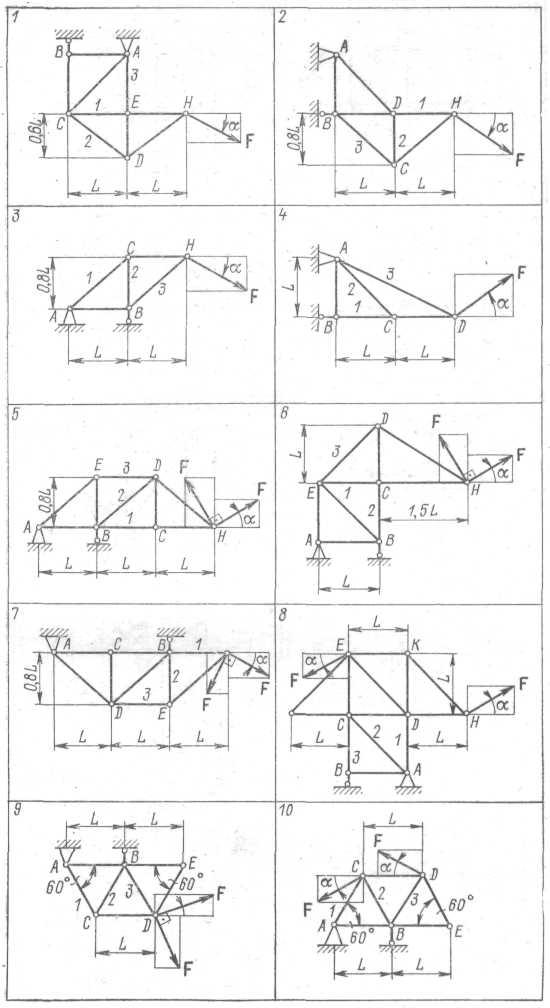
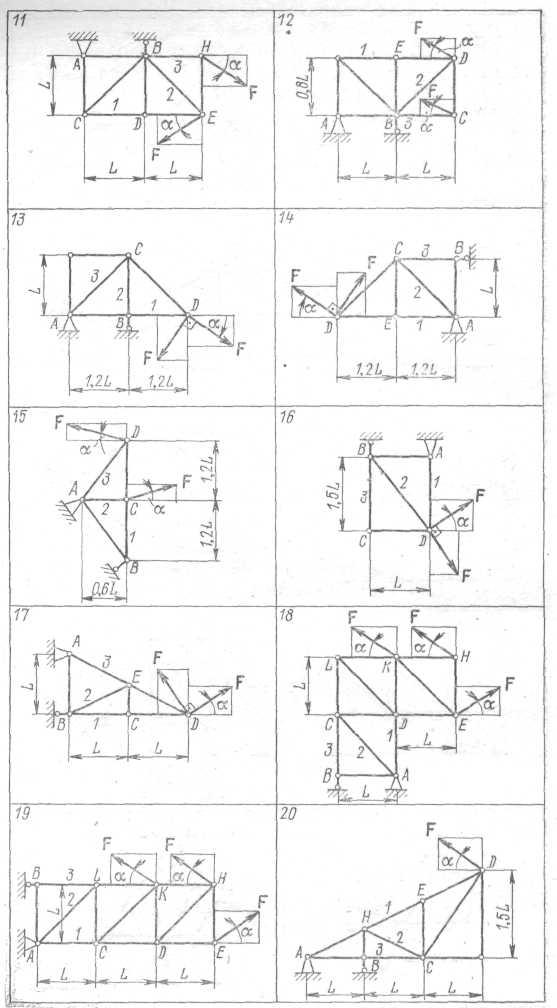
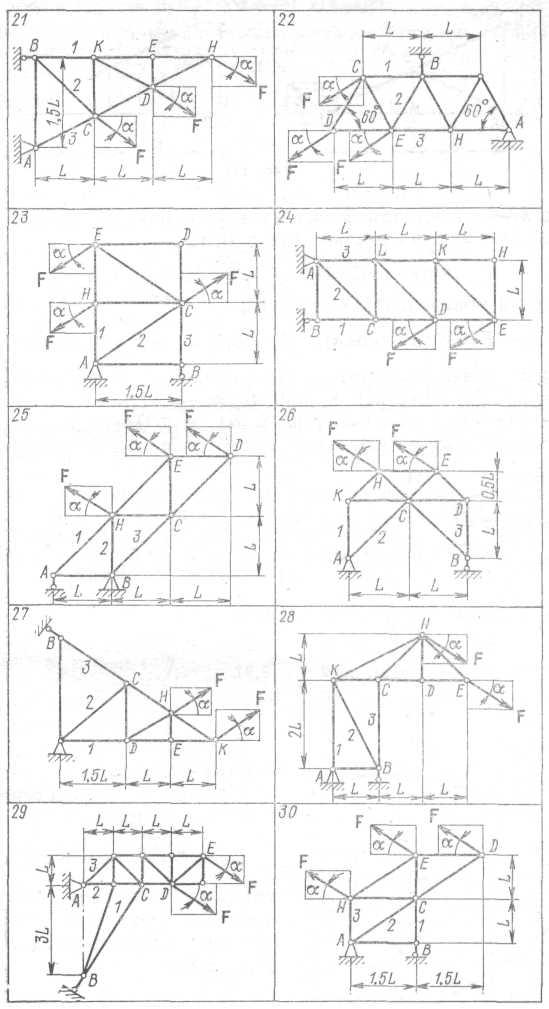
Рис. 3.1

Пример. Определить усилия в стержнях 1 - 3 фермы (рис. 3.2,а), к которой приложена заданная сила F = 2 кН, наклоненная под углом α = 60° к горизонту.

Рис. 3.2

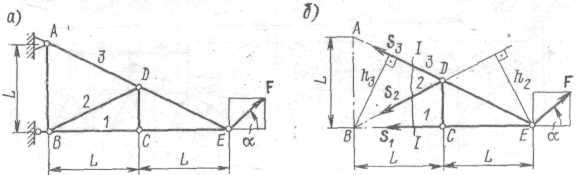
Решение. Для определения усилий в стержнях мысленно разрежем ферму сечением 1 − 1 и рассмотрим равновесие правой части фермы (рис. 3.2,6). Действие отброшенной части фермы представим искомыми силами S₁, S₂ и S₃. При этом предположим, что все стержни растянуты.

Затем составим три уравнения равновесия для правой части фермы таким образом, чтобы в каждое из них входило не более одного неизвестного усилия

∑M_D (F_k) = 0; F sin α · L + F cos α · L/2 − S₁L/2 = 0;

∑M_E{F_k) = 0; S₂h₂ = 0; (3.1)

∑M_B (F_k) = 0; F sin α · 2L + S₃h₃ = 0.

Здесь h₂ − плечо силы S₂ относительно точки Е; h₃ = BE sin β — плечо силы S₃ относительно точки В, где

sin β = АВ/АЕ = 1/√5, h₃ = 2L/√5

Решая систему уравнений (1), получим

S₁ = F (2 sin α + cos α); S₂ = 0; S₃ = − F √5 sin α.

Знак минус показывает, что стержень 3 сжат. При F = 2 кН·и α = 60° S₁ = 4,46 кН; S₂ = 0; S₃ = − 3,87 кН.

Результаты вычислений по приведенным S₁ S₂ S₃ формулам следующие:

α,°. . . . . . . . . . . . . 0 15 90

S₁, кН . . . . . . . . . 2 2,97 4

S₃, кН . . . . . . . . . 0 -1,16 -4,47

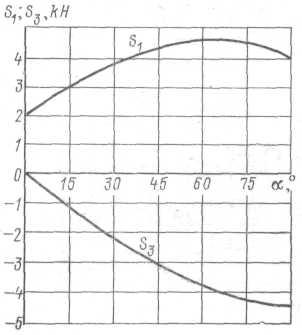
На рис. 4 приведены графические зависимости S₁(α) и S₂(α).Анализ графиков зависимостей позволяет определить наименьшие и наибольшие значения усилий:

S_1max = 4,5 кН, α = 60°, S_1min = 2 кН, α = 0°; S_3max = 5 кН, α = 90°, S_3min = 0 кН, α = 0°.

Рис. 3.3

ЗАДАНИЕ 2

РАСЧЕТ ДИНАМИЧЕСКИХ НАГРУЗОК ГРУЗОПОДЪЕМНОГО МЕХАНИЗМА

Определить динамические нагрузки грузоподъемного механизма при его работе, размеры и кинематические характеристики движения звеньев которых приведены в табл. 2_. Вид грузоподъемного механизма для исследования выбрать из рис. 2_ в соответствии с заданием.

Таблица 2_

N схемы	L, м	a, м	b, м	r, м	G, кН	φo	φmax	M, кН*м	F, кН	m1, т	m2, кг	m3, кг	u, м/с	ω, рад/с
1	1	0,2	-	-	12	45	90	-	12	1,2	100	-	1	2
2	-	0,2	2	0,2	2	-	-	0,1	-	1	50	-	-	2
3	1	0,2	-	-	30	0	30	-	10	3	40	-	-	2
4	1	2	-	0,2	15	0	90	1,5	-	1,5	50	-	1	-
5	4	0,5	0,5	-	10	0	30	-	50	1	150	-	2	-
6	-	1	2	-	10	0	60	1	-	1	50	-	-	2
7	-	1	2	0,2	10	-	-	4	-	1	50	-	-	2
8	3	0,5	1,2	-	15	0	30	-	100	1,5	300	-	1	-
9	3	1	1	-	15	30	60	-	130	1,5	300	-	1	-
10	2	1	-	0,2	20	30	120	2,5	-	2	900	100	-	1
11	1,5	0,5	0,5	-	20	0	90	-	20	2	100	20	-	2
12	3	1	-	-	2	45	90	-	4	10	360	-	1	-
13	3	1	-	0,2	30	30	90	10	-	3	100	-	-	2
14	1	1	-	-	10	0	45	-	30	1	300	-	2	-
15	3	1	3	0.2	200	30	90	12	-	20	100	-	-	1
16	3	3	2	-	50	30	90	-	120	5	300	-	1	-
17	3	5	5	0,2	50	30	90	8	-	5	600	100	-	2
18	-	2	-	0,4	10	-	-	0,1	-	1	100	-	-	2
19	-	0,5	2	-	10	-	-	-	5	1	50	-	1	-
20	1	0,5	-	-	6	0	45	5	1	0,6	10	-	-	1
21	1	-	-	-	30	0	60	-	12	3	50	-	-	2
22	1	-	-	-	9	0	90	-	5,5	0,9	300	10	-	1
23	1	-	-	-	10	30	90	1	1	1	30	-	2	-
24	2	1,8	0,25	-	9	0	90	-	100	0,9	-	-	2	-
25	-	-	0,3	0,4	60	0	90	-	50	6	25	-	-	2
26	1	0,5	-	-	3	0	90	1	20	0,12	20	300	-	1
27	1	2	-	-	3	30	90	0,7	1	0,3	2	-	-	2
28	1	0,5	-	-	10	0	90	-	20	1	300	-	-	2
29	4	4	-	0,1	100	0	30	20	-	10	3000	200	-	1
30	-	0,2	0,3	-	5	0	90	-	-	-	500	50	2	-

Обозначение: т – тонна, 1 т = 1000 кг.

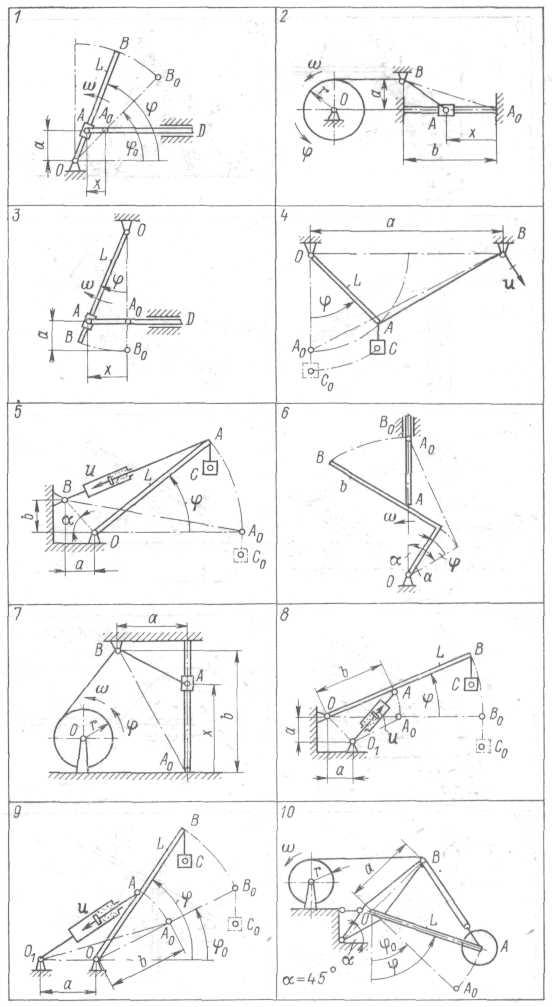
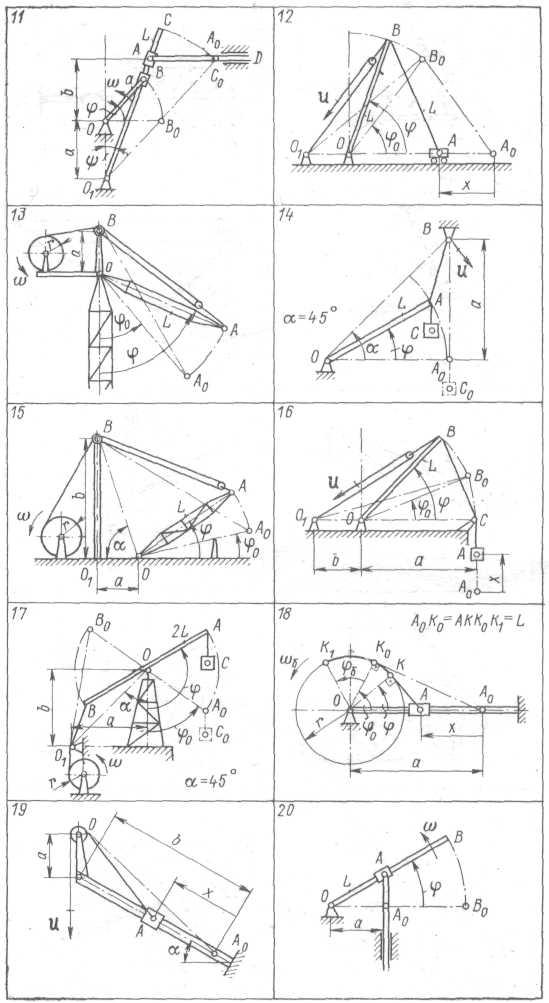
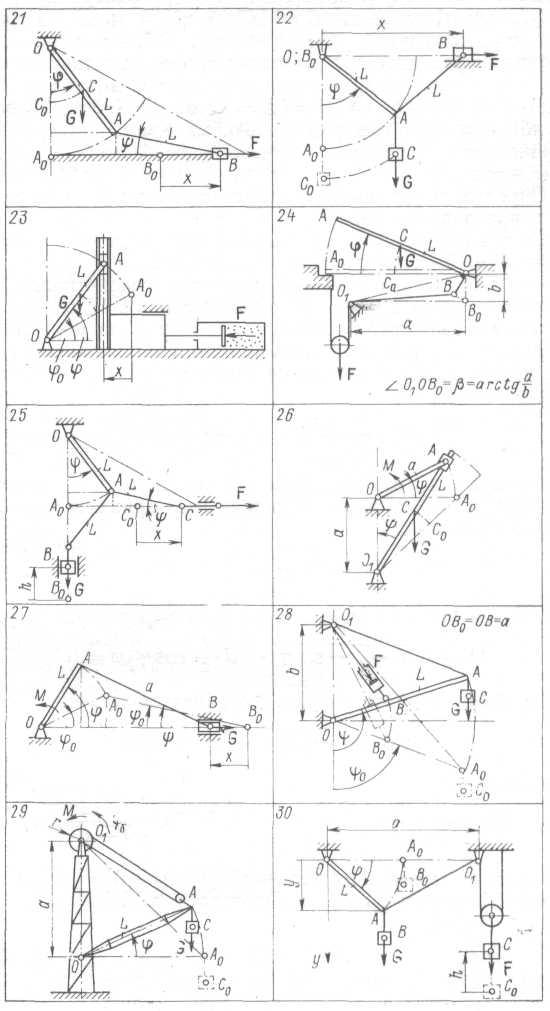
Рис. 2_

4. ПОСТУПАТЕЛЬНОЕ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЯ СТРЕЛЫ

Найти скорость и ускорение точки А одного из звеньев механизма (рис. 2_). Вычислить значения v_A и а_А при перемещении механической системы в трех точках. Построить графики указанных параметров.

Примечание. Ускорение а_А может быть найдено путем дифференцирования выражения v_A по времени t.

Пример. Груз В поднимается с помощью стрелы ОА и троса, перекинутого через неподвижный блок D, размерами которого можно пренебречь (рис. 4.1,а).

Известно, что стрела ОА имеет длину 2 м и вращается с постоянной угловой скоростью ω = 0,2 рад/с, а расстояние OD = 4 м.

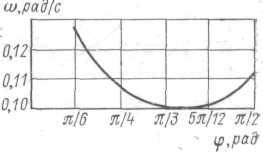
Определить скорость v и ускорение а груза В, а также скорость и ускорение точки А стрелы при угле поворота φ = π/2. Вычислить значений функций v = v(φ) и а = а(φ) при изменении угла φ от π /6 до π /2 и построить их графики по трем точкам.

Определить угловую скорость ω и угловое ускорение ε стрелы, при которых скорость груза В будет постоянной и равной 0,2 м/с. Вычислить угловую скорость и угловое ускорение стрелы, а также скорость и ускорение точки А стрелы при φ = π/2. Вычислить значения функций ω = ω(φ) и ε = ε (φ) при изменении φ от π /6 до π /2 и построить их графики.

Рис. 4.1

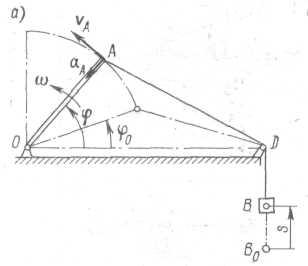
Решение. Скорость груза определяется по формуле

v = ds/dt,

где s − перемещение груза при повороте стрелы на угол φ.

Это перемещение равно изменению длины троса между точками D и В при повороте стрелы

s = AD - A₀D,

где длины отрезков AD и A₀D определяются из треугольников ОАО и OA₀D по теореме косинусов

AD = (2² + 4² − 2 · 2 · 4 cos φ)^½ = 2 (5 − 4 cos φ)^½

A₀D = 2 (5 − 4 cos π/6)^½.

Тогда скорость груза

v = d/dt [2(5 − 4 cos φ)^½ − 2(5 − 4 cos π/6)^½ ] =

= 4 sin φ · φ^’ /(5 − 4 cos φ) ^½.

Так как φ^’ = ω = 0,2 рад/с, то окончательно получим

v = 0.8 sin φ /(5 − 4 cos φ) ^½. (1)

Ускорение груза

a = v^’ = 0.8 [cos φ (5 − 4 cos φ)^½ − 2 sin² φ /(5 − 4 cos φ)^½] _· φ^’ /(5 − 4 cos φ) =

= 0.16 [cos φ (5 − 4 cos φ)^½ − 2 sin² φ /(5 − 4 cos φ)^½] /(5 − 4 cos φ). (2)

При φ = π/2 v = 0,358 м/с, а = − 0,0286 м/с².

Скорость точки А стрелы

v_A = ω ОA = 2.2 · 2 = 0,5 м/с.

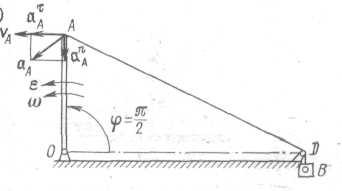
Вектор v_A направлен по касательной к траектории точки А в сторону вращения стрелы (см. рис. 4.1,а). Ускорение точки А

a_А = a^τ_A + aⁿ_A,

где a^τ_A, aⁿ_A — касательное и нормальное ускорения точки A.

Касательное ускорение

a^τ_A = ε ОA = 0,

так как стрела вращается с постоянной угловой скоростью и ее угловое ускорение ε = ω^’ = 0. Нормальное ускорение

aⁿ_A = ω² ОA = 0,2² · 2 = 0,08 м/с².

Вектор aⁿ_A направлен к оси вращения стрелы. Таким образом, a_A = aⁿ_A и a_A = 0,08 м/с².

Угловую скорость стрелы, при которой скорость груза В будет постоянной и равной v = 0,2 м/с, определим из выраже­ния (1):

ω = φ^’ = 0.2 (5 − 4 cos φ)^½ / 4 sin φ = 0.05 (5 − 4 cos φ)^½ / sin φ.

Угловое ускорение стрелы

ε = ω^’ = 0.05 d/dt [(5 − 4 cos φ)^½ / sin φ] =

0.05 [ 2 sin² φ / (5 − 4 cos φ)^½ − (5 − 4 cos φ)^½ cos φ ] φ^’ / sin² φ.

При φ = π/2 ω = 0,05√5 = 0,1118 рад/с; ε = 0,005 рад/с²; v_A=ω OA = 0,1118·2 = 0,2236 м/с; aⁿ_A = ω² OA == 0,1118²/2 = = 0,025 м/с²; a^τ_A = ε OA = 0,005·2 = 0,01 м/с²; а_A = (a^τ_A² + aⁿ_A²) = 0.0269 м/с².

Векторы v_A, a^τ_A , aⁿ_A, а_A показаны на рис. 4.1.

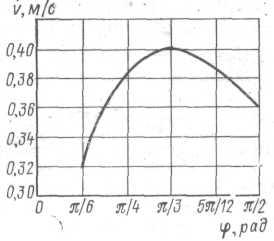
Результаты вычислений по формулам (1), (2) значений кинематических параметров груза следующие:

φ, рад . . . . . . . . . . π/6 π/4 π/3 π/2

v_, м/с . . . . . . . . . . 0,323 0,384 0,4 0,358

a, м/с² . . . . . . . . . . 0,069 0,267 0 -0,029

Графики функций v = v(φ) и a = a(φ) приведены на рис. 4.2

Рис. 4.2

5. СЛОЖНОЕ ДВИЖЕНИЕ ГРУЗА ПРИ ЕГО ПЕРЕМЕЩЕНИИ

Найти относительную, переносную и абсолютную скорости точки А, а также ее абсолютное ускорение механизма (рис. 2_). Вычислить значений функций v_r, v_e, v_A, a_A при перемещении точки А в заданных пределах. Построить графики указанных функций.

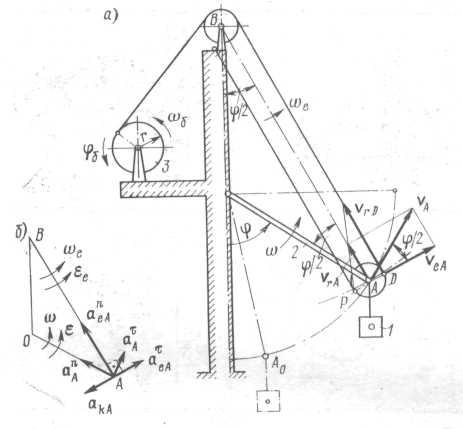
Рис. 5.1

Пример. Груз 1 поднимается с помощью грузоподъемного устройства (рис. 5.1,а), которое состоит из грузовой стрелы 2, лебедки 3, подвижного и неподвижного блоков, соединенных с помощью троса. Барабан лебедки вращается по закону φ₆ = 2t рад. Известно, что ОА = OB = L = 3 м, r = 0,2 м. Трос считается гибким и ерастяжимым.

Определить абсолютную скорость v_A и абсолютное ускорение а_А груза как функции угла поворота стрелы φ и построить графики v_A = v_A (φ) и а_А = а_А (φ). Угол φ изменяется от 15 до 90^°.

Решение. Груз 1 совершает поступательное движение. Поэтому скорость и ускорение его центра тяжести равны скорости и ускорению оси подвижного блока А. Движение точки А рассматриваем как сложное, которое складывается из переносного и относительного движений.

В относительном движении точка А двигается вдоль линии АВ со скоростью v_rA. В переносном движении в данный момент времени траекторией точки А является окружность радиуса АВ и переносная скорость v_eA направлена по касательной к этой окружности (см. рис. 5.1, а). По теореме о сложении скоростей находим абсолютную скорость точки А

v_A = v_eA + v_rA.

Для определения относительной скорости v_rA учтем, что подвижный блок вращается в данный момент времени вокруг оси, которая проходит через его мгновенный центр скоростей Р. Тогда

v_rA = v_rD / 2,

где v_rD − скорость намотки троса на барабан лебедки.

Скорость намотки троса на барабан

v_rD = ω_б · r,

где ω₆ − угловая скорость барабана, ω₆ = φ^’_б = 2 рад/с. Окончательно находим

v_rA = ω₆ · r /2 = 0,2 м/с.

Из параллелограмма скоростей следует

v_A = v_rA / sin(φ/2) = ω₆ · r / (2 – 2 cos φ)^½ = 0,4 / (2 – 2 cos φ)^½ (1)

Угловая скорость грузовой стрелы

ω = φ^’ = v_A/OA = v_A / 3.

Абсолютное ускорение точки А определяется по теореме о сложении ускорений

а_A = a_eА + а_rA + а_kA,

где a_eА , а_rA , а_kA — переносное, относительное и кориолисово ускорения точки А.

Поскольку в относительном движении точка А движется вдоль прямой АВ с постоянной скоростью v_rA = 0,2 м/с, то ее относительное ускорение

а_rA = v^’_rA = 0.

Траекторией переносного движения точки в данный момент времени является окружность радиуса АВ (рис. 5.1,6). Поэтому переносное ускорение складывается из касательного a^τ_eА и нормального aⁿ_eА ускорений

a_eА = a^τ_eА + aⁿ_eА.

Переносное нормальное ускорение определяется из выражения

aⁿ_eА = ω ²_e АВ,

где ω _е − переносная угловая скорость;

АВ = 2L cos (φ/2) = L (2 + 2 cos φ)^½ .

Переносная угловая скорость

ω _е = v_eA / AB = v_rA ctg(φ/2) / 2L cos (φ/2) = ω_б · r / 4L sin (φ/2) =

= ω_б · r / L (2 + 2 cos φ)^½ = ω / 2.

Переносное касательное ускорение определяем из выражения

а^τ_еА = ε_е АВ,

где ε_е − переносное угловое ускорение,

ε_е = ω^’_е = ω_б · r / 2L · [ 1 / (2 + 2 cos φ)^½ ]^’ = − ω_б · r sin φ · φ^’ / 4L((2 − 2 cos φ)^½ )³ =

= - ω²_б · r² sin φ / 8L² (1 − cos φ) ² = − 0,0022 sin φ / (1 − cos φ) ².

Модуль кориолисова ускорения определяем по формуле

а_кА = 2ω_е v_rА sin(ω_е ^ v_rА) = 2ω_e v_rA,

так как угол между векторами ω_е и v_rА равен 90° .

Направление вектора а_кА устанавливается по правилу Жу­ковского: через точку А проводится плоскость, перпендикуляр­ная вектору ω_е; определяется проекция вектора v_rA на эту пло­скость; проекция вектора v_rA поворачивается на угол 90° в сто­рону вращения. Полученный вектор и дает направление а_кА.

Так как составляющие ускорения а_А направлены по двум взаимно перпендикулярным прямым, то модуль абсолютного ускорения

а_А = [(a^τ_eА − a_kА)² + (aⁿ_eА)²]^½.

Можно предложить и другой способ вычисления абсолют­ного ускорения точки А. Поскольку траекторией точки А в аб­солютном движении является окружность радиуса ОА, то аб­солютное ускорение можно представить в виде векторной суммы

a_А = a^τ_А + aⁿ_А ,

где a^τ_А и aⁿ_А − касательное и нормальное ускорения точки А.

Касательное ускорение точки А в абсолютном движении

a^τ_А = v^’_е = ω_б · r / [ 1 / (2 − 2 cos φ)^½ ]^’ = − ω_б · r sin φ · φ^’ / 2L((2 − 2 cos φ)^½ )³ =

= - ω²_б · r² sin φ / 4L² (1 − cos φ) ² = - 0,0133 sin φ / (1 − cos φ) ².

Нормальное ускорение точки А в абсолютном движении

aⁿ_A = v_A /OA = v_A / L.

Модуль абсолютного ускорения

а_А = [(a^τ_eА)² + (aⁿ_eА)²]^½.

Результаты вычислений приведены ниже:

φ, ° . . . . . . . . . . . . . . . . . . . . 15 30 60

v_A, м/с . . . . . . . . . . . . . . . . . 1,53 0,77 0,4

ω, рад/с . . . . . . . . . . . . . . .. 0,51 0,25 0,13

ω_e, рад/с . . . . . . . . . . . . . 0,25 0,13 0,066

AB, м . . . . . . . . . . . . . . . 5,94 5,79 5,19

aⁿ_eА, м/с² . . . . . . . . . . . . 0,38 0,09 0,023

ε_е, рад/с² . . . . . . . . . . . – 0,49 - 0,06 - 0,007

a^τ_eА, м/с² . . . . . . . . . . . . – 2,95 - 0,35 - 0,04

a_kА, м/с² . . . . . . . . . . . . . 0,102 0,051 - 0,035

а_А, м/с² . . . . . . . . . . . . . . 3,08 0,42 0,07

Графики функций v_A := v_A (φ) и а_А = а_А (φ) приведены на рис. 5.2.

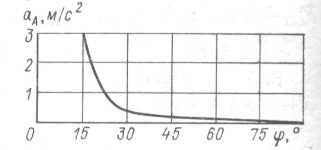
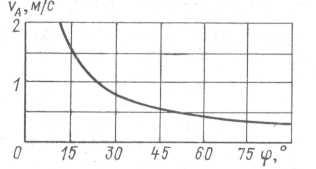
Рис. 5.2

6. ИЗМЕНЕНИЕ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ЭЛЕМЕНТОВ МЕХАНИЗМА

Определить с помощью теоремы об изменении кинетиче­ской энергии в интегральной форме угловую скорость или скорость одного из тел системы в соответствии с указаниями табл. 2_.Вычислить значения функций, указанных в табл. 2_, с представлением их в виде графиков.

В начальный момент времени система находится в покое. Нити являются гибкими и нерастяжимыми. Массами подвижных и неподвижных блоков и нитей, а также трением в опорах пренебречь. Барабаны считать сплошными однородными дисками.

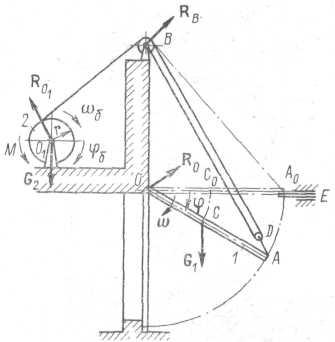
Рис. 6.1

Пример. Затвор 1, закрывающийся под действием собственного веса, представля­ет собой однородную прямоугольную пластину массой m₁ = 15 000 кг, имеющую возможность вращаться вокруг горизонтальной оси О (рис.60). Для уменьшения удара затвора об упоры в нижнем положении к барабану 2, связанному с затвором посредством троса, приложен тормозящий момент М = 1 кН · м. Масса барабана m₂ = 200 кг, радиус r = 0,2 м. Барабан представляет собой сплошной однородный диск. Затвор удерживается в горизонтальном положении фиксатором Е. Известно, что ОА = OB = L = 3 м. Трос следует считать гибким и нерастяжимым, массой подвижного D и неподвижного В блоков, массой троса а также трением в опорах и сопротивлением воздуха можно пренебречь. Размеры блоков принимаются малыми.

Определить угловую скорость ω затвора при его опускании после снятия фиксатора как функцию угла поворота и построить график ω = ω(φ).

Решение. Рассмотрим движение механической системы, состоящей из твердых тел 1 и 2, соединенных гибкой нерастяжимой нитью, переброшенной через подвижный и неподвижный блоки. К системе приложены силы тяжести G₁ и G₂ затвора и барабана, тормозящий момент М, а также реакции шарнирных неподвижных опор R_O, R_O1, Rs.

Для определения угловой скорости ω затвора воспользуемся теоремой об изменении кинетической энергии

T – T₀ = ∑ A^e_k. (6.1)

где T₀ и Т − кинетическая энергия системы в начальном и конечном положениях: ∑ A^e_k − сумма работ внешних сил, приложенных к системе, при ее перемещении из начального в конечное положение.

Так как в начальный момент времени система находится в покое, то T₀ = 0.

Величина Т равна сумме кинетических энергий всех тел си­стемы:

T = T₁ + T₂. (6.2)

Учитывая, что затвор 1 и барабан 2 совершают вращательное движение вокруг неподвижных осей, проходящих через точки О и О₁, имеем

T₁ = J₁ω² /2; T₂ = J₂ω² /2, (6.3)

где ω − угловая скорость затвора, ω = φ^’; φ − угол поворота затвора; ω_б − угловая скорость барабана, ω_б = φ^’_б; φ_б − угол поворота барабана; J₁ − момент инерции затвора относительно оси вращения, Ji = m₁L²/3; J₂ − момент инерции барабана, J₂ = m₂r²/2.

Угловую скорость ω_б и угол поворота φ_б барабана следует выразить через угловую скорость ω и угол поворота φ затвора соответственно. Для этого надо определить длину троса, наматываемого на барабан при повороте затвора на угол φ, учитывая, что D подвижный, а В − неподвижный блоки. Эта длина равна

∆L = 2 (BA - BA₀),

где

ВА₀ = L√2 ; ВА = (ОА² + ОВ² - 2 · ОА · ОВ cos (90^° + φ)) ^½=

= L √2 (1 + sin φ)^½.

Тогда

φ_б = ∆L / r = 2 · L/r · √2 · ((1 + sin φ)^½ - 1) (6.4)

и

ω_б = φ^’_б = √2· L/r · cos φ · φ^’ / (1 + sin φ)^½ = √2· L/r · (1 – sin² φ)^½ / (1 + sin φ)^½ · φ^’ =

= √2· L/r · (1 – sin φ)^½ (1 + sin φ)^½ / (1 + sin φ)^½ · φ^’ = √2· L/r · (1 – sin φ)^½ · φ^’. (6.5)

Подставив величины (6.3) и (6.4) в равенство (6.2), получим

T = ½ · [m₁L² /3 + m₂L² (1 – sin φ)] · ω². (6.6)

Найдем сумму работ внешних сил при повороте затвора на угол φ

∑ A^e_k = G₁ · L/2 · sin φ – M · φ_б = m₁g · L/2 · sin φ –

− M · 2 · L/r · √2 ·((1 + sin φ)^½ − 1). (6.7)

Работа силы тяжести G₂ и реакций связей R_O, R_O1, R_B равна нулю, так как точки приложения этих сил неподвижны. Подставляя выражения (6.6) и (6.7) в уравнение (6.1) и учитывая, что Т₀ = 0, получим равенство

1/2 · [m₁L² /3 + m₂L² (1 – sin φ)] · ω² =

= m₁g · L/2 · sin φ – M · 2 · L/r · √2 ·((1 + sin φ)^½ − 1).

откуда находим квадрат искомой угловой скорости затвора

ω² = 2 / (m₁L² /3 + m₂L² (1 – sin φ)) ·

· [m₁g · L/2 · sin φ – M · 2 · L/r · √2 ·((1 + sin φ)^½ − 1)].

или, с учетом численных значений m₁, m₂, L, r, g,

ω² = 2 / (45000 + 1800 (1 – sin φ)) · [220725 sin φ – 42426 ((1 + sin φ)^½ − 1)].

Результаты вычислений следующие:

φ, ° . . . . . . . . . . 0 30 60 90

ω, рад/с . . . . . 0 2,1 2,8 3,0

График зависимости ω = ω(φ) представлен на рис.6.2.

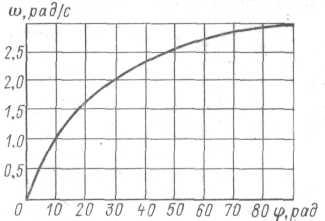
Рис. 6.2.

7. ИССЛЕДОВАНИЕ РАВНОВЕСИЯ С ИСПОЛЬЗОВАНИЕМ ПРИНЦИПА

ВОЗМОЖНЫХ СКОРОСТЕЙ.

Определить с помощью принципа возможных скоростей зависимость между вращающим моментом М или силой F и силой G при равновесии. Вычислить значения функций М = М(G) или F = F(G) при изменении угла φ или перемещения x одного из звеньев системы в заданных преде­лах с изображением их в виде графиков.

Пример. Затвор 1 представляет собой однородную прямо­угольную пластину весом G = 147,15 кН и может вращаться вокруг горизонтальной оси (рис. 7.1). Затвор удерживается в положении равновесия с помощью троса, намотанного на барабан 2, к которому приложена пара сил с моментом M.

Известно, что ОА = OB = L = 3 м, r = 0,2 м. Трос считать гибкой и нерастяжимой нитью, массой и размерами бло­ков пренебречь. Трение отсутствует.

Определить зависимость момента М от угла поворота затвора φ при равновесии. Вычисления значений функции М = М(φ) и построить ее график.

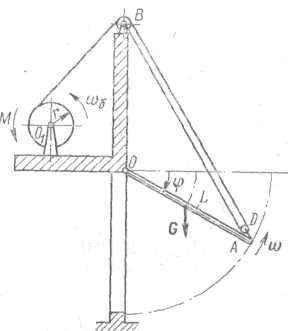
Рис. 7.1

Решение. Связи системы являются голономными, удерживающими, идеальными и стационарными. Система имеет одну степень свободы. Сообщим барабану 2 возможную угло­вую скорость сое, при этом затвор 1 получит угловую скорость φ. Зависимость между угловыми скоростями ω_б и ω была установлена ранее

ω_б = L/r · √2 · (1 – sin φ)^½.

Уравнение возможной мощности заданных активных сил, приложенных к системе, выражающее принцип возможных скоростей, имеет вид

M · ω_б – G · L/2 · cos φ · ω = 0.

После подстановки значения «б в это уравнение получим

(M · L/2 · √2 · (1 – sin φ)^½ - G · L/2 · cos φ) · ω = 0

Поскольку ω ≠ 0, то должно выполняться условие

M · L/2 · √2 · (1 – sin φ)^½ - G · L/2 · cos φ = 0,

откуда следует

M = G · r · cos φ / (2√2 · (1 – sin φ)^½) = 10405,08 · cos φ / (1 – sin φ)^½.

Результаты вычислений функции М = М(φ) следующие:

φ,^° . . . . . . . . . . . 0 30 60 90

М,кН·м . . . . .10405,07 12743,56 14 213,59 20 099,75

График зависимости М = М(φ) приведен на рис. 7.2.

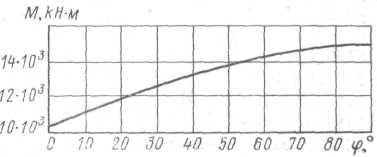
Рис. 7.2

8. РАСЧЕТ ИНЕРЦИАЛЬНЫХ ХАРАКТЕРИСТИК С ИСПОЛЬЗОВАНИЕМ

УРАВНЕНИЯ ЛАГРАНЖА

Определить с помощью уравнений Лагранжа второго рода: угловое ускорение стержня 1 для схем 1, 3, 4, 13, 15, 20, 21, 24−27, 30; угловое ускорение стержня 2 для схем 5, 8−11, 14, 17, 22, 28, 29; ускорение тела 1 для схем 2, 6, 7, 12, 16, 18, 19, 23. Вычислить значения функций ε = ε(φ), а = а(х) или а = а(φ) для тел. Построить графики этих функций.

Пример. Определить угловое ускорение ε = φ′′ затвора 1 механической системы (рис. 8.1), рассмотренной в примере п.6. Построить графики функций a = a(φ), ω = ω(t), φ = φ(t), ε = ε(t).

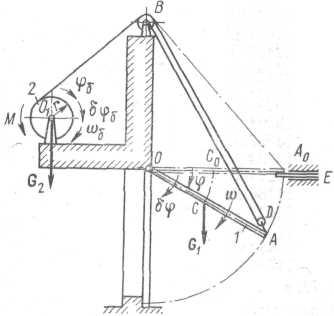
Рис. 8.1

Решение. Механическая система имеет одну степень свободы. В качестве обобщенной координаты примем угол поворота φ затвора 1.

Уравнение Лагранжа второго рода, соответствующее выбранной обобщенной координате, имеет вид

d/dt · ∂T/∂φ^’ - ∂T/∂φ = Q_φ, (8.1)

где Т − кинетическая энергия системы; Q_φ − обобщенная сила.

Кинетическая энергия системы была определена ранее и при ω = φ^’’

T = [m₁L²/3 + m₂L²(1 – sin φ)] · φ^’2/2.

Кинетическая энергия барабана 2 составляет менее 5 % от кинетической энергии затвора 1, поэтому можно принять кине­тическую энергию системы равной

T = 1/2 · m₁L²/3 · φ^’2.

Находим значения производных, которые входят в уравнение (8.1)

∂T/∂φ = 0; ∂T/∂φ^’ = m₁L²/3 · φ^’; d/dT ∂t/∂φ^’ = m₁L²/3 · φ’’.

Для определения обобщенной силы Q_φ дадим системе возможное перемещение, сообщив обобщенной координате φ приращение δφ. При этом угол поворота барабана φ_б получит при­ращение δφ_б. Составим сумму возможных работ заданной силы G и тормозящего момента М на возможном перемещении системы

δA_φ = Q_φ · δφ = G₁ · L/2 · cos φ · δφ – M · δφ. (8.2)

Для определения δφ_б необходимо найти изохронную вариацию функции (6.4),

φ_б = 2 L/r · √2 · ((1 + sin φ)^½ - 1).

Учитывая, что операции варьирования и дифференцирования функции аналогичны, найдем

δφ_б = L/r · √2 · (1 - sin φ)^½ .

(Зависимость между δφ_б и δφ такая же, как между ω_б и ω).

После подстановки δφ_б в выражение (8.2) получим

δA_φ = Q_φ · δφ = [m₁g · L/2 · cos φ – M · L/r ·√2 · (1 – sin φ)^½] · δφ.

Отсюда находим обобщенную силу

Q_φ = δA_φ /δφ = m₁g · L/2 · cos φ – M · L/r ·√2 · (1 – sin φ)^½_.

Подставив найденные значения производных и обобщенной силы в уравнение Лагранжа, имеем

m₁g · L/3 · φ′′ = m₁g · L/2 · cos φ – M · L/r ·√2 · (1 – sin φ)^½

Отсюда находим угловое ускорение затвора 1

φ′′ = 3/m₁L² · (m₁g · L/2 · cos φ – M · L/r ·√2 · (1 – sin φ)^½).

или, с учетом численных значений m₁, L, r, g

φ′′ = 2,22 · 10^-3 [220725 cos φ – 21213 (1 – sin φ)^½].

Результаты вычислений зависимости φ′′ = φ′′(φ) следу­ющие:

φ,° . . . . . . . . . . . . . 0 30 60 90

φ′′, рад/с² . . . . . . . 4,43 3,91 2,28 0

График зависимости φ′′ = φ′′(φ) приведен на рис. 8.2.

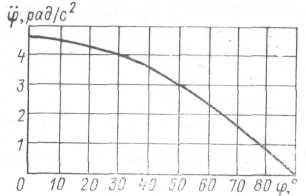
Рис. 8.2

СОДЕРЖАНИЕ

Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

Содержание курса . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

Задание 1. Расчет статических нагрузок на конструкции . . . . . . . . . . . . . . . . . . . . . . . . 8

1. Определение реакции опор и заделки консольных балок . . . . . . . . . . . . . . . . . . . . . . 8

2. Опорные реакции конструкций . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13

3. Определение усилий в стержнях плоской фермы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18

Задание 2. Расчет динамических нагрузок грузоподъемного механизма . . . . . . . . . . . . 22

4. Поступательное и вращательное движение стрелы . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26

5. Сложное движение груза при его перемещении . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28

6. Изменение кинетической энергии элементов механизма . . . . . . . . . . . . . . . . . . . . . . 30

7. Исследование равновесия механизма с помощью принципа возможных скоростей . 33

8. Расчет инерциальных характеристик с использованием уравнения Лагранжа . . . . . 34