
- •Элементы аналитической геометрии
- •§1. Метод координат на плоскости
- •1. Декартовы прямоугольные координаты
- •2. Полярные координаты
- •3. Связь между прямоугольной декартовой системой координат и полярной системой координат.
- •4. Основные задачи, решаемые методом координат
- •§2. Уравнение линии на плоскости
- •§3. Прямая линия
- •1. Виды уравнения прямой.
- •2. Основные задачи на использование уравнения прямой
- •§4. Кривые второго порядка
- •1. Основные понятия
- •2. Окружность
- •3. Эллипс.
- •3. Гипербола
- •5. Парабола
§2. Уравнение линии на плоскости
Прямоугольная и полярная система координат позволяет задавать различные линии на плоскости их уравнениями.
Уравнением линии на плоскости в прямоугольной системе координат называется уравнение f(x;y)=0 с переменными х и у, которому удовлетворяют координаты каждой точки данной линии и не удовлетворяют координаты любой точки плоскости, не лежащей на этой линии.
§3. Прямая линия
1. Виды уравнения прямой.
I. Уравнение прямой с угловым коэффициентом.
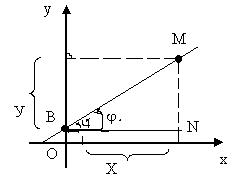
Рассмотрим
MNB
- прямоугольный , найдем tg=![]() ;
;
tg - угловой коэффициент прямой,
tg
=к, к=![]() ;
;
(1) у=кх+b –
уравнение прямой с угловым коэффициентом, где b – начальная ордината.
Пример1.
Дан угол
=![]() и нач. ордината b=-3.
Составить уравнение прямой.
и нач. ордината b=-3.
Составить уравнение прямой.
Решение.
у=кх+b,
(к=tg)
к=tg![]() =1
у=х-3
=1
у=х-3
Если в уравнении (1) к=0, то прямая L параллельна оси Ох и ее уравнение имеет вид: у=b; при b= 0 и к = 0, получаем уравнение оси Ох: у=0.
Прямая х=а параллельна оси Оy, при а=0 получим уравнение оси Оу: х=0.
II. Общее уравнение прямой.
Уравнением с угловым коэффициентом может быть задана любая прямая на плоскости, не параллельная оси ординат.
При рассмотрении уравнения 1-ой степени
(2) Ах+Ву+С=0,
в котором а и в одновременно не обращаются в 0 , окажется, что любую прямую без каких-либо ограничений можно задать уравнением (2).
Теорема. Каждая прямая на плоскости с прямоугольной декартовой системой координат определяется уравнением 1-ой степени и наоборот, каждое уравнение 1-ой степени определяет некоторую прямую на плоскости.
Доказательство:
I. 1.Пусть дана прямая l, не параллельная Оу l : у= кх+b, у– кх– b=0
-кх+у–b=0.
Пусть А=-к, В=1, С=-b, получим что любая прямая не параллельная оси Оу задается уравнением (2).
Пусть дана l параллельная оси Оу l : х=а , х–а=0.
Положим А=1, В=0, С=-а и прямая, параллельная оси Оу задается уравнением (2), т.е. любую прямую на плоскости можно определить уравнением 1-ой степени.
II. Пусть Ах+Ву+С=0.
1. Пусть В0.
Выразим у: Ву=-Ах–С; у=-![]() ·х-
·х-![]() т.е. к=-
т.е. к=-![]() ; b=-
; b=-![]()
уравнение (2) задает на плоскости прямую
не паралелльную оси Оу.
уравнение (2) задает на плоскости прямую
не паралелльную оси Оу.
2. Если в (2) В=0
А0
Ах+С=0
х=![]() ,
т. е. получим уравнение прямой параллельной
оси Оу, т.е. (2) задает на плоскости прямую.
,
т. е. получим уравнение прямой параллельной
оси Оу, т.е. (2) задает на плоскости прямую.
Уравнение (2) называется общим уравнением прямой.
III. Уравнение прямой с данным угловым коэффициентом и проходящей через данную точку.
Пусть дана точка М1 (х1; у1)l и к- угловой коэффицмент прямой. Составить уравнение прямой.
l: у=кх+b, т.к. М1l, то ее координаты удовлетворяют этому уравнению: у1 =кх1+b. Вычтем из первого уравнения второе:
(3) у–у1=к(х–х1) - уравнение прямой с данным угловым коэффициентом и проходящей через данную точку.
Пример 1. Составить уравнение прямой, проходящей через точку М (-1; 8), если к = 1.
Используем уравнение (3).
у–8=1(х+1) у–8=х+1, у=х+9.
IV. Уравнение прямой, проходящей через 2 данные точки.
Пусть прямая проходит через точки М1(х1;у1) и М2(х2;у2) и не параллельна оси Оу. Требуется составить ее уравнение.
Используем уравнение (3) прямой, проходящей через точку М1:у–у1=к(х–х1).
Необходимо найти
к. Так как точка М2
лежит на прямой, то ее координаты
удовлятворяют этому уравнению:
у2–у1=к(х2–х1).
Поскольку прямая не параллельна оси
Оу, то х1х2.
Поэтому
![]() .
Подставим в уравнение (3):
.
Подставим в уравнение (3):
у–у1=![]() (х–х1).
Разделим обе части на у2-у1:
(х–х1).
Разделим обе части на у2-у1:
(4)![]() - уравнение прямой, проходящей через 2
данные точки.
- уравнение прямой, проходящей через 2
данные точки.
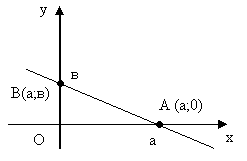
V. Уравнение прямой в отрезках по осям координат.
Предположим, что в (2) А0, В0, С 0, тогда преобразуем уравнение:
Ах+Ву+С=0, Ах+Ву=-С,
![]() ·х-
·х-![]() ·у=1;
·у=1;
![]()
![]() =1.
=1.
Обозначим
![]() =а,
=а,
![]() =b;
тогда
=b;
тогда
( 5)
5)![]()
![]() =1
- уравнение прямой в отрезках по осям
координат.
=1
- уравнение прямой в отрезках по осям
координат.
Числа а и b определяют длины отрезков, которые прямая отсекает на осях координат.
Заметим, что прямые параллельные осям координат и прямые, проходящие через начало координат не могут быть записаны уравнениями в отрезках.
П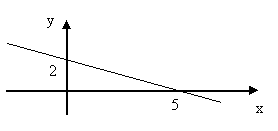 ример
2. Записать
уравнение прямой 2х+5у–10=0 в отрезках и
построить данную прямую.
ример
2. Записать
уравнение прямой 2х+5у–10=0 в отрезках и
построить данную прямую.
2х+5у=10,
![]()
![]() =1
=1
