Алгоритм rsa шифрования с открытым ключом (р.Ривест, а.Шамир, л.Адлеман, 1978 г.).

1. Получатель генерирует открытый ключ – пару чисел n и e.

• Выбираются два простых числа p и q, p ≠ q.

• Определяется первая часть открытого ключа – число n = pq.

• Определяется вторая часть открытого ключа – небольшое нечетное число e, взаимно простое с (p-1)(q-1)=φ(n) (любое с таким свойством).

Открытый ключ n и e сообщается всем отправителям сообщений.

2. Получатель генерирует закрытый ключ: d=e^-1mod(p-1)(q-1), то есть 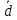–обратный элемент для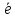в полеℤ*_(p-1)(q-1), то есть 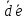=или

de≡1(mod(p-1)(q-1))

Закрытый ключ хранится в секрете.

3. Отправитель шифрует сообщение, разбивая его на слова α_i<n, (т.е. длина α_i менее log₂n двоичных разрядов) по правилу

β_i=(α_i )^emod n. (1)

4. Получатель расшифровывает сообщение с помощью закрытого ключа d по правилу

γ_i=(β_i )^dmod n. (2)

Теорема 1. При шифровании RSA дешифровка производится корректно, то есть γ_i=α_i.

Доказательство: Из алгоритма следует,

(1) β_i=(α_i )^emod n β_i≡(α_i )^e(mod n), 0 ≤ β_i <n, (3)

(2) γ_i=(β_i )^dmod n γ_i≡(β_i )^d(mod n), 0 ≤ γ_i <n. (4)

Возведем обе части (3) в степень d: (α_i )^ed ≡β_i^d(mod n)≡ γ_i(mod n). С учетом транзитивности,

(α_i )^ed ≡ γ_i (mod n). (5)

_{Поскольку} e и d – взаимно обратны по модулю (p-1)(q-1), то 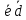=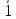, то есть 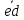=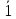⇔ed≡1(mod(p-1)(q-1)) следовательно,

ed=1+(p-1)(q-1)k, kℤ. (6)

Докажем, что для любого x<n выполняется

x^ed≡x(mod p). (7)

а) Пусть x≢0(mod p), значит, x не кратен p, и, так как p – простое число, то (x, p)=1, следовательно, по теореме Ферма, x^φ(p)≡1(mod p), то есть x^p-1≡1(mod p). Тогда x^ed=x^{1+(p-1)(q-1)k}=x‧(x^p-1)^(q-1)k≡x‧1^(q-1)k(mod p)≡x(mod p).

б) Пусть x≡0(mod p), т.е. x кратен p. Возведем обе части сравнения в степень ed: x^ed≡0(mod p) и из транзитивности отношения сравнимости следует x^ed≡x(mod p).

Таким образом, для любого x < n выполняется (7).

Аналогично доказывается, что для любого x<n

x^ed≡x(mod q). (8)

Из (7) и (8) следует x^ed≡x(mod p), x^ed≡x(mod q). По теореме 4, (следствие теоремы об остатках), с учетом (p, q)=1 получаем x^ed≡x(mod pq), т.е. для любого x<n

x^ed≡x(mod n). (9)

Так как в алгоритме RSA двоичные сообщения α_i имеет длину |α_i|< log₂n, то α_i является двоичным числом, меньшим 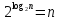. Тогда

(9) ⇒ (α_i)^ed≡α_i(mod n),

(5) ⇒(α_i)^ed≡γ_i(mod n).

С учетом транзитивности отношения сравнимости, α_i≡γ_i(mod n). И так как α_i<n и γ_i<n, то α_i=γ_i. Теорема доказана.

Криптостойкость системы RSA объясняется сложностью разложения открытого числа n на простые множители. Эффективный алгоритм для этого найден лишь для отдельных случаев. Чтобы их избежать, выполняют требования:

а) p и q – достаточно большие, не слишком близки, но не слишком отличаются друг от друга;

б) желательно, чтобы НОД(p-1; q-1)=2 или был небольшим;

в) p и q – сильно простые числа (r сильно простое число, если r+1 имеет большой простой делитель, r-1 имеет большой простой делитель s и s-1 имеет большой простой делитель).

_{Недостатки системы RSA.}

_{- медленная работа при больших e и снижение криптостойкости при малых e.}

_{- разработаны и постоянно совершенствуются программы и компьютеры способные быстро разлагать большие числа на простые множители.}