
- •2. Матрицы. Основные определения – прямоугольная, квадратная, диагональная, треугольная, нулевая и единичная матрицы. Сложение матриц и его свойства.
- •3. Умножение матрицы на скаляр, транспонирование матриц, умножение матриц и их основные свойства.
- •4. Перестановки n-й степени. Теорема о четности перестановки. Определители n-го порядка. Определители второго и третьего порядков.
- •5. Разложение определителя по ряду. Минор и алгебраическое дополнение к элементу определителя. Связь алгебраических дополнений с минорами.
- •6. Свойства определителей.
2. Матрицы. Основные определения – прямоугольная, квадратная, диагональная, треугольная, нулевая и единичная матрицы. Сложение матриц и его свойства.
Определение 1. Матрицей размера m×n над полем Р называется прямоугольная таблица, состоящая из n строк и m столбцов, следующего вида:
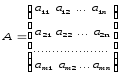 ,
где aij
,
где aij
 P,
i=
P,
i=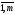 ,j=
,j=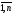 .
.
Определение 2. Квадратной матрицей n-го порядка над полем P называется матрица размера n×n над полем P.
Пусть A – квадратная матрица n-го порядка. Тогда в А выделяют 2 диагонали: главную и побочную.



главная побочная
Матрицы
обозначаются следующим образом: А=(aij)
или А=||aij||,
i=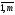 ,j=
,j=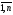 .
.
Определение 3. Элементы aii квадратной матрицы А=(aij) называются диагональными, или элементами главной диагонали.
Определение 4. Квадратная матрица А=(aij) называется диагональной, или все ёё элементы, кроме элементов главной диагонали, равны нулю: aii≠ 0, aij=0 при i≠j.
Через
Аi
будем
обозначать i-ю
строку матрицы А, т.е. Аi=(ai1
ai1
… ain),
через Аj
– j-й
столбец матрицы А, т.е. Аj
= .
.
Определение
5.
Матрица А=(aij),
i= ,j=
,j=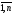 называется треугольной (верхней
треугольной), если aij=0
при
i>j.
называется треугольной (верхней
треугольной), если aij=0
при
i>j.
Строку или столбец матрицы А называют нулевыми, если все их элементы равны нулю.
Определение
6.
Матрица А=(aij),
i=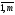 ,j=
,j=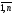 называется ступенчатой
(матрицей
ступенчатого вида),
если во всех ее строках вторые индексы
первых слева ненулевых элементов
называется ступенчатой
(матрицей
ступенчатого вида),
если во всех ее строках вторые индексы
первых слева ненулевых элементов
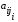 возрастают
j1<j2<…<ji.
возрастают
j1<j2<…<ji.
Из определения 6 следует, что ступенчатая матрица является треугольной, причем ее нулевые строки (если они есть) расположены ниже ее ненулевых строк.
Определение
7.
Две матрицы A=(aij)
и B=(bij)
размера m×n
над полем P
называются равными,
если aij=bij,
i=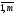 ,j=
,j=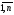 .
Обозначается А=В.
.
Обозначается А=В.
Определение
8.
Матрица над полем P
называется нулевой,
если все ее элементы равны нулю.
Обозначается
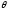 =
= .
.
Определение
9.
Матрица n-го
порядка вида
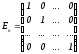 называетсяединичной
матрицей.
Другими словами, единичная матрица —
это диагональная матрица у которой все
элементы главной диагонали равны 1:
aii=1
для всех i.
называетсяединичной
матрицей.
Другими словами, единичная матрица —
это диагональная матрица у которой все
элементы главной диагонали равны 1:
aii=1
для всех i.
Определение
10.
Пусть A=(aij),
B=(bij)
- матрицы размера m×n
над полем Р.
Суммой
матриц
А
и В
называется матрица С=(cij)
размера m×n
над полем Р,
где cij=aij+bij,
i=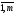 ,j=
,j=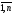 ,
и обозначаетсяС=А+В.
,
и обозначаетсяС=А+В.
Теорема.
Для любых матриц А , В и С размера m×n
над полем P
выполняются следующие свойства: 1)
А+В=В+А; 2) А+(В+С)=(А+В)+С; 3) А+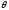 =
=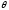 +А=А;
4) для любой матрицы А над полемP
существует матрица (-А) такая, что
А+(-А)=-А+А=
+А=А;
4) для любой матрицы А над полемP
существует матрица (-А) такая, что
А+(-А)=-А+А=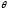 .
.
Доказательство. Так как сложение матриц сводится к сложению элементов поля Р, а в поле Р сложение коммутативно и ассоциативно, существует нулевой элемент и для каждого элемента есть противоположный, то эти свойства выполняются и для матриц.
Множество всех матриц размера m×n над полем P обозначается через Мm,n(Р). Из теоремы следует, что Мm,n(Р) является аддитивной абелевой группой.
3. Умножение матрицы на скаляр, транспонирование матриц, умножение матриц и их основные свойства.
Определение
1.
Пусть A=(aij)
– матрица размера m×n
над полем P,
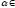 P.
Произведением
матрицы А на элемент
P.
Произведением
матрицы А на элемент
 называется матрицаС=(сij)
размера m×n
над полем P,
где сij=
называется матрицаС=(сij)
размера m×n
над полем P,
где сij=
 aij
,
j=
aij
,
j=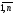 ,i=
,i=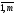 ,
и обозначается С=
,
и обозначается С= А.
А.
Определение
2.
Пусть A=(aij)
– матрица размера m×n
над полем P,
B=(bij)
- матрица размера n×k
над полем P.
Произведением
матриц А и
В
называется матрица С=(сij)
размера m×k
над полем P,
в которой элемент сij
равен скалярному произведению i-й
строки матрицы А
на j-й
столбец матрицы B,
т.е. сij=AiBj=(ai1
...
ain)⋅ =ai1b1j+…+ainbnj=
=ai1b1j+…+ainbnj=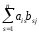 ,i=
,i=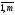 ,j=
,j=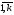 ,
и обозначается С=A⋅B.
,
и обозначается С=A⋅B.
Лемма 1. Пусть А, В, С - матрицы над полем Р. Если существует произведение (АВ)С, то существует и произведение А(ВС), причем (АВ)С=А(ВС).
Доказательство. Пусть существует произведение (АВ)С. Тогда существуют матрицы АВ размера m×n и матрица С размера n×k. Это означает, что существуют матрицы А размера m×l и В размера l×n. Таким образом, существуют матрицы А, В и С соответственно размера m×l, l×n и n×k. Тогда существует произведение BC размера l×k и поэтому существует произведение А(ВС).
Покажем,
что (AB)C=A(BC).
Пусть (АВ)С=(xij),
А(ВС)=(yij),
i=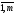 ,j=
,j=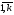 .
Покажем, что xij=yij,
i=
.
Покажем, что xij=yij,
i=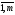 ,j=
,j=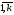 .
Пусть A=(aip),
B=(bps),
С=(сsj),
АВ=R=(ris),
BC=T=(tpj),
s=
.
Пусть A=(aip),
B=(bps),
С=(сsj),
АВ=R=(ris),
BC=T=(tpj),
s=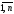 ,p=
,p=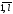 .Тогда
.Тогда
xij=RiCj=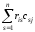 =
=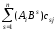 =
=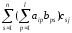 =
= ,
,
yij=AiTj=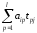 =
=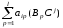 =
=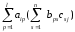 =
=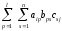 .
.
Таким
образом, xij=yij
, i=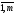 ,j=
,j=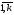 .
Следовательно, (AB)C=A(BC).
Лемма доказана.
.
Следовательно, (AB)C=A(BC).
Лемма доказана.
Лемма 2. Пусть A, B, C – матрицы над полем P следующих размеров: А и В – размера m×n, С – размера n×k. Тогда (А+В)С=АС+ВС.
Доказательство.
Пусть (А+В)С=(xij),
АС+ВС=(yij),
i=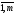 ,
j=
,
j=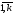 .
Покажем,
что
xij=yij,
i=
.
Покажем,
что
xij=yij,
i= ,
j=
,
j=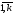 .
Пусть
A=(ais),
B=(bis),
С=(сsj),
i=
.
Пусть
A=(ais),
B=(bis),
С=(сsj),
i=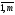 ,
s=
,
s=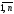 ,
j=
,
j=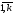 .
Тогда
.
Тогда
xij=(A+B)iСj=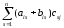 =
=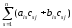 =
=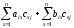 =AiCj+BiCj=yij.
=AiCj+BiCj=yij.
Следовательно, (А+В)С=АС+ВС. Лемма доказана.
Определение
3.
Пусть A
- матрица размера m×n
над полем P.
Транспонированием
матрицы А
называется операция замены в матрице
А
i-й
строки на i-й
столбец, i=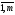 .
Матрица, полученная в результате
транспонирования матрицы A,
называется матрицей, транспонированной
к матрице A,
и обозначается tA.
.
Матрица, полученная в результате
транспонирования матрицы A,
называется матрицей, транспонированной
к матрице A,
и обозначается tA.
Пример
1.
Если A
= ,
тоtА
=
,
тоtА
= .
Таким образом, еслиА
– матрица размера m×n,
то tА
- матрица размера n×m.
.
Таким образом, еслиА
– матрица размера m×n,
то tА
- матрица размера n×m.
Лемма 3. Если произведение AB существует, то существует произведение tB tA, причем t(AB)= tB tA.
Лемма 4. Если А – матрица размера m×n над полем Р, то АЕn=EnA=A.
Доказательство осуществляется непосредственной проверкой.
Через Mn(P) обозначается множество всех квадратных матриц n-го порядка над полем P.
Замечание. Из свойств операций над матрицами следует, что Mn(P) - ассоциативное кольцо с единицей. Отметим, что умножение матриц некоммутативно (см. примеры на практических занятиях).
Лемма
5.
Пусть А
и
В – матрицы
над полем P,
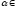 P.
Тогда
P.
Тогда
 AB=(
AB=( A)B=A(
A)B=A( B).
B).
