Размещено на http://www.allbest.ru/

Введение

Появление современных вычислительных машин привело к своему роду революции в численных методах. Сейчас численные методы применяются во многих разделах математики. Среди задач с которыми приходится иметь дело в вычислительной практике значительную часть составляют различные задачи дифференциальных уравнений в частных производных. Такие задачи возникают непосредственно при математическом моделировании многих реальных физических явлений в таких областях, как динамика жидкости, электричество и магнетизм, оптика, теплопередача.

Аналитические методы позволяют найти точное решение задачи лишь для ограниченного класса уравнений, поэтому в начале XIX века широко развиваются численные методы решений дифференциальных уравнений, такой как метод сеток. Конечно-разностные методы решения уравнений в частных производных были предложены еще в 1928 году в знаменитой статье Куранта, Фридрихса и Леви, но на практике эти методы стали применяться лишь 15 лет спустя. Отметим, что члены Лос-Аламосского персонала в Абердине численно решили на машине ЭНИАК сложные задачи, относящиеся к системам уравнений в частных производных. Вслед за тем в различных местах США были решены многие задачи, связанные с движением жидкостей и газов, диффузией и переносом нейронов, переносом лучистой энергии, термоядерными реакциями.

На сегодняшний день решение уравнений параболического типа численными методами актуально, так как нахождение аналитического решения задачи в явном виде, т. е. получение формулы, характеризующей зависимость функции состояния системы от координат и параметров процесса, удается найти лишь в исключительных случаях. Как правило, находится лишь приближенное решение задачи. Среди множества способов практического анализа выбран метод численного решения метод сеток в виду его достаточно высокой эффективности и чрезвычайно широкой популярности. При этом рассматриваемая область разбивается на участки, на каждом из которых соответствующие производные аппроксимируются некоторыми разностными схемами. В дипломной работе рассматриваются дифференциальные уравнения в частных производных параболического типа, решаемые разностными методами.

Целью исследования является рассмотрение основных методов решения дифференциальных уравнений в частных производных конечно-разностными методами: однородные и консервативные конечно-разностные схемы для задач теплопроводности с граничными условиями, содержащими производные; неявно-явная конечно-разностная схема с весами; схема Кранка-Николсона; метод дробных шагов Н.Н. Яненко; метод переменных направлений с экстраполяцией В.Ф. Формалева.

Предметом исследования считаются численные методы решения дифференциальных уравнений в частных производных параболического типа.

Основными задачами написания дипломной работы являются

Рассмотрение сути методов: неявно-явной конечно-разностной схемы с весами; схемы Кранка-Николсона; метода дробных шагов Н.Н. Яненко; метода переменных направлений с экстраполяцией В.Ф. Формалева; однородные и консервативные конечно-разностные схемы для задач теплопроводности с граничными условиями, содержащими производные;

Рассмотрение достоинств и недостатков исследуемых методов дифференциальных уравнений в частных производных параболического типа.

Написание программ для типовых задач.

Для решения задач использовались математическая система MathCAD 7.0 Professional Edition (PRO) и язык программирования Turbo Pascal 6.0.

Системы MathCAD традиционно занимают особое место среди множества таких систем (Eureka, Mercury, MatLAB, Mathematica 2 и 3, Maple V R3 и R4 и др.) и по праву могут называться самыми современными, универсальными и массовыми математическими системами. Они позволяют выполнять как численные, так и аналитические (символьные) вычисления, имеют чрезвычайно удобный математико-ориентированный возможности и прекрасные средства графики. Системы класса MathCAD предоставляют уже привычные, мощные, удобные и наглядные средства описания алгоритмов решения математических задач. Система имеет достаточные возможности для выполнения наиболее массовых символьных (аналитических) вычислений и преобразований.

Turbo Pascal 6.0, так как этот язык позволяет работать с математическими формулами, приводить различного рода математические операции и действия. Turbo Pascal фирмы Borland является расширением стандарта языка и содержит интегрированную среду, данного ускоряющую и облегчающую процесс разработки программ. В языке программирования Turbo Pascal 6.0 используется типизированный адресный оператор, открытые массивы и строки, что предоставляет пользователю дополнительные возможности при решении математических задач.

На защиту выносится методика вычисления решений дифференциальных уравнений в частных производных параболического типа численными методами – метод сеток, вопросы устойчивости и аппроксимации решения дифференциальных уравнений в частных производных параболического типа, а также анализ численного решения типовых примеров.

Практической значимостью считается решение дифференциальных уравнений в частных производных параболического типа численными методами.

При написании данной дипломной работы была изучена литература следующих авторов: Киреев В.И., Пантелеев А.В. «Численные методы в примерах и задачах»; Формалев В.Ф., Ревизников Д.Л. «Численные методы»; Рихтмайер Р.Д. «Разностные методы решения краевых задач»; Вержбицкий В.М. «Основы численных методов»; Демидович Б.П., Марон И.А. «Основы вычислительной математики»; Данко П.Е., Попов А.Г., Кожевникова Т.Я. «Высшая математика в примерах и задачах»; Кабдыкайыр К. «Курс математики»; Плис А.И., Сливина Н.А. «Лабораторный практикум по высшей математике»; Такабаев М.К. «Курс высшей математики».

1. Дифференциальные уравнения в частных производных

1.1 Определение дифференциальных уравнений в частных производных параболического типа

Физические явления в таких областях, как динамика жидкости, электричество и магнетизм, механика, оптика, теплопередача, описываются с помощью дифференциальных уравнений в частных производных. Производные появляются в уравнениях потому, что они описывают важнейшие физические величины (такие, как скорость, ускорение, сила, поток, трение, электрический ток и т.д.). В отличие от обыкновенных дифференциальных уравнений, в которых неизвестная функция зависит только от одной независимой переменной, в уравнениях с частными производными неизвестная функция зависит от нескольких переменных.

Наиболее часто встречаются дифференциальные уравнения второго порядка.

Определение 1. Уравнением с частными производными второго порядка с двумя неизвестными переменными x и y называется соотношение между неизвестной функцией 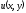и её частными производными до второго порядка включительно:

(1.1)

В общем случае уравнение в частных производных может быть записано в виде

(1.1)

где – независимые переменные,- неизвестная (искомая) функция,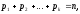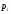- целые неотрицательные числа.

Определение 2. Уравнение называется линейным относительно старших производных, если оно имеет вид

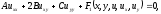(1.2)

где 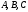являются функциями x и y.

Определение 3. Если коэффициенты 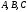зависят не только от x и y, а являются, подобно F1, функциями то уравнение называется квазилинейным.

Определение 4. Уравнение называется линейным, если оно линейно как относительно старших производных так и относительно функции u и ее первых производных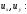

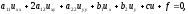(1.3)

где 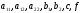- функции только x и y.

Определение 5. Если коэффициенты уравнения (1.3) не зависят от x и y, то оно представляет собой линейное уравнение с постоянными коэффициентами.

Определение 6. Уравнение (1.3) называется однородным, если 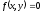, в противном случае неоднородным.

Задачи математической физики состоят в отыскании решений уравнений в частных производных, удовлетворяющих некоторым дополнительным условиям. Такими дополнительными условиями чаще всего являются условия, заданные на границе рассматриваемой среды, т. е. граничные условия и начальные условия, относящиеся к одному какому-нибудь моменту времени, с которого начинается изучение данного физического явления.

Определение 7. Задача математической физики считается поставленной корректно, если решение задачи, удовлетворяющее всем ее условиям, существует, единственно и устойчиво.

Устойчиво, т. е. в данных любой конкретной задачи, особенно если они получены из опыта, всегда содержится погрешность и нужно, чтобы малая погрешность а данных приводила к малой неточности в решении. Требование существования и единственности означает, что среди данных задачи нет несовместных и их достаточно для выделения единственного решения.

1.2 Приведение уравнения второго порядка параболического типа к каноническому виду

Рассмотрим уравнение 2-го порядка с двумя независимыми переменными, линейное относительно производных второго порядка:

(1.4)

где A,B и C – функции, зависящие от x и y, имеющие непрерывные производные до 2-го порядка включительно.

С помощью преобразования переменных

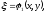
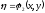(1.5)

допускающего обратное преобразование получим новое уравнение. Пусть (1.5) дважды непрерывно дифференцируемые функции, причем якобиан

(1.6)

в рассматриваемой области.

Преобразуя производные к новым переменным, получаем:

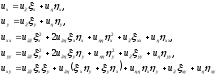(1.7)

Подставляя значения производных из (1.7) в уравнение (1.4), будем иметь

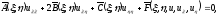(1.8)

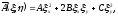
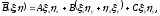
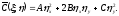
Непосредственной подстановкой нетрудно проверить, что

(1.9)

Рассмотрим дифференциальное уравнение 1-го порядка

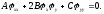(1.10)

Исследуем случай, когда во всей рассматриваемой области 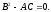Тогда уравнение (1.4) принадлежит параболическому типу. Пусть в рассматриваемой области коэффициенты уравнения (1.4) не обращаются одновременно в нуль. В силу условия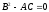из этого предположения следует, что в каждой точке этой области один из коэффициентов A и C отличен от нуля. Не нарушая общности, можно считать, что в рассматриваемой области всюду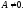Тогда уравнение (1.10) можно записать в виде

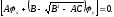
Это уравнение распадается на два:

(1.10а)

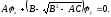(1.10б)

Решения каждого из уравнений (1.10а) и (1.10б) будут решениями уравнения (1.10). Оба уравнения (1.10а) и (1.10б) совпадают и обращаются в уравнение

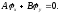(1.11)

Всякое решение уравнения (1.11), в силу 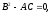удовлетворят также уравнению

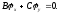(1.12)

Для интегрирования уравнений (1.10а) и (1.10б) составим соответствующие им системы обыкновенных дифференциальных уравнений

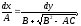
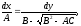
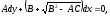(1.13)

.

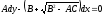Уравнение (1.13) можно записать в виде одного уравнения

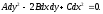(1.13а)

Пусть

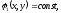
(1.14)

интегралы уравнений (1.13). Тогда их левые части будут решениями уравнений (1.10а) и (1.10б), а значит и уравнения (1.10). Кривые (1.14) называются характеристическими кривыми или просто характеристиками уравнения (1.4), а уравнение (1.10) – уравнением характеристик.

Для уравнения параболического типа интегралы (1.14) совпадают, и получаем семейство вещественных характеристик

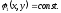
Возьмем

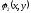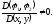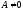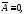где решение уравнения решение уравнения (1.11), а за– любую функцию так, чтобы якобианТак каки, следовательно,то можно принять. Тогда в уравнение (1.8)что следует из (1.9), а коэффициент припринимает следующий вид:

Согласно (1.11) и (1.12) 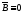в рассматриваемой области. Коэффициентв уравнении (1.8) преобразуется к виду

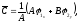
откуда 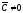, так как в противном случае в силу (1.11) якобиан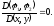Разделив на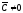уравнение (1.8) приведем его к виду

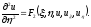(1.15)

Это канонический вид уравнения параболического типа.

Если уравнение (1.4) линейно, то и уравнение (1.15) также будет линейным:

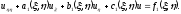(1.16)