Задачи с параметрами и методы их решения

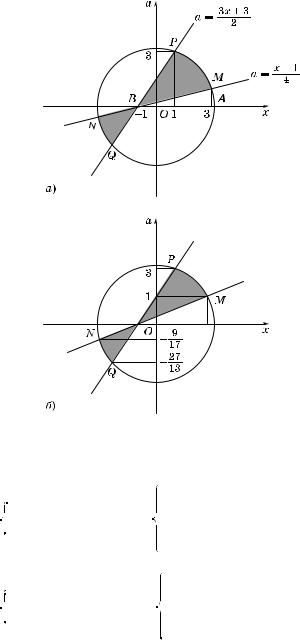
Рис. 38

6. Рассмотрим два случая:

3x – 2a + 3 l 0, а) x – 4a + 1 m 0,

воряют точ и ду#и PM);

3x – 2a + 3 m 0, б) x – 4a + 1 l 0,

воряют точ и ду#и NQ).

или

или

am

al

al

am

3x + 3

---------------- ,

2

x + 1

(этой системе удовлет-

------------

4

3x + 3

---------------- ,

2

x + 1

(этой системе удовлет-

------------

4

141

7. Найдем ординаты точе Q, P, N, M о ружности. Для это#о нужно решить две системы уравнений:

								x =	----------------2a – 3		,
а)			3x – 2a + 3 = 0,						3				от уда a =		6 ä 33		,
			x2 + a2 = 10					2a – 3		2	2				-------	13------------
								-------	3---------		+ a	= 10,
т. е. a			------= – 27 , a	2	= 3.
1	13
б)			x – 4a + 1 = 0,				x = 4a – 1,						от уда a =	4 ä 13		, т. е.
			x2 + a2 = 10				17a2 – 8a – 9 = 0,							-------17--------	----

9

a3 = –------ , a4 = 1.

17

8.Остается записать значения a, соответствующие ду#ам MP

иNQ. Эти значения a определяют верти альные отрез и на оси Oa (рис. 38, б).

279

9.Ответ: a Ý –------ ; –------ Ÿ [1; 3].

1317

29.При а их значениях a орни уравнения

	x2 – 2x – a2 + 1 = 0	(1)
лежат между орнями уравнения
	x2 – 2(a + 1)x + a(a – 1) = 0?	(2)
1.	Находим орни уравнения (1):
	x1 = 1 – |a|, x2 = 1 + |a|, x1 m x2.
2.	Находим орни уравнения (2):
	x3 = a + 1 – 1 + 3a , x4 = a + 1 + 1 + 3a , x3 m x4.
3.	Корни уравнения (2) являются действительными при условии

1

a l –-- . Требуется найти та ие a, чтобы выполнялись неравенства

3

a + 1 – 1 + 3a < 1 – |a| m 1 + |a| < a + 1 + 1 + 3a .

(3)

4. Пусть a < 0; то#да неравенства (3) примут вил

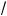a + 1 – 1 + 3a < 1 + a m 1 – a < a + 1 + 1 + 3a .

142

В этом случае достаточно, чтобы удовлетворялось лишь неравенство

1 – a < a + 1 + 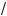1 + 3a ,

или

–2a < 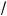1 + 3a ,

#де –2a > 0.

5.Возводя в вадрат правую и левую части последне#о неравенства, после преобразований получим неравенство 4a2 – 3a – 1 < 0,оторое выполняется при a Ý (–0,25; 1). Та а a < 0, то поставленная задача имеет решение при a Ý (–0,25; 0).

6.Пусть теперь a l 0; то#да неравенства (3) примут вид

a + 1 – 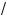1 + 3a < 1 – a m 1 + a < a + 1 + 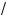1 + 3a .

В этом случае достаточно, чтобы удовлетворялось лишь неравенство

a + 1 – 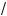1 + 3a < 1 – a,

или

2a < 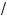1 + 3a ,

#де 2a l 0.

7.Возводя в вадрат правую и левую части последне#о неравенства, после преобразований получим неравенство 4a2 – 3a – 1 < 0,оторое выполняется при a Ý (–0,25; 1). Та а в рассматриваемом случае a l 0, то поставленная задача имеет решение при a Ý

Ý[0; 1).

8.Ита , орни уравнения (1) лежат между орнями уравнения (2), если –0,25 < a < 1.

9.Ответ: a Ý (–0,25; 1).

30. При а их значениях параметра a существует единственная пара целых чисел (x; y), удовлетворяющая смешанной системе

–15x2 + 11xy – 2y2 = 7,

x < y,

2a2x + 3ay < 0?

1. Перепишем уравнение данной системы в виде

(y – 3x)(5x – 2y) = 7.

(1)

143

2.Та а по условию числа x и y должны быть целыми, то целыми будут и числа y – 3x и 5x – 2y.

3.Поэтому все целые числа x и y, оторые удовлетворяют уравнению (1), найдем из следующих четырех систем уравнений:

y – 3x = –1, 5x – 2y = –7;

y – 3x = –7, 5x – 2y = –1;

y – 3x = 1, 5x – 2y = 7;

y – 3x = 7, 5x – 2y = 1.

(2)

(3)

(4)

(5)

4.Решениями систем (2), (3), (4), (5) являются соответственно пары чисел (9; 26), (15; 38), (–9; –26), (–15; –38).

5.Второму соотношению данной системы удовлетворяют пары чисел (9; 26) и (15; 38).

6.Подставив значения x = 9, y = 26 в третье соотношение дан-

ной системы, придем неравенству 3a2 + 13a < 0, решением ото-

13

ро#о являются все a та ие, что –------ < a < 0.

3

7. Подставив значения x = 15, y = 38 в третье соотношение данной системы, придем неравенству 5a2 + 19a < 0, решением ото-

19

ро#о являются все a та ие, что –------ < a < 0.

5

8. Требованию задачи будут удовлетворять те значения параметра a, оторые удовлетворяют аждому из неравенств пп. 6 и 7.

9.	Ответ: a Ý		13	19		.
			–------ ; –------
			3	5

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. Найти значения a, при оторых орень уравнения a2(x – 3) – a(4x – 13) = 34 – 4x не меньше, чем 4.

2. Установить, при а их значениях a система неравенств:

а)		3	– 6x < 2x – 13,	не имеет решений;
		3	+ 2x < a + x

144

имеет единственное решение.

б)			–2(a + 4x) < x – 3,	имеет хотя бы одно решение;
			5 – 3x > 2 + 4(x – a)
			2x – (a + 1)y l 2a + 2,
в)			(a – 5)x + 4y l a – 9	имеет решение;

y – x m2, #) 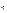y – 2x l a,

ax + y l 2

3. Решить систему неравенств:

a(x – 2) l x – 3,

а) 8(a + 1)x > 8ax + 9;

	------------ax	<	----------------2x + 3	------------+ x – 1	,
	a – 2		4	3
б)
	----------------x(a –	-------- ---------------------10) + 6 > a(x + 2)				– 5x – a.
	2			2

4. Установить, при а их значениях a неравенство:

а) (a – 3)x2 – 2ax + 3a – 6 > 0 выполняется для всех значений x;

б) -----ax----------	<	3--	выполняется для всех значений x;
a2 + 4		2

в) (a – 1)x2 + 2(a + 1)x + 2a – 1 m 0 выполняется толь о для одно#о значения x;

x – 2a – 1

#) ------------------------- < 0 справедливо для всех x Ý [1; 2]? x – a

5. При а ом значении a уравнение |x2 – 2x – 3| = x + a имеет ровно один орень?

6. При а их значениях a двойное неравенство

x2 + ax – 2

–2 < ----------------------------- < 3 x – 1 – x2

выполняется для всех значений x?

7. Найти все значения a, при оторых орни уравнения

(a – 2)x2 – 2(a + 4)x + 4a = 0

имеют одина овые зна и. 8. Решить неравенство:

а)	a	> 3; б)	x	–	2a	<	8a2
	2----a-----–------x-		------------		--------		x----2-----	--------- .
			x – a x + a					– a2

9. При а их значениях параметра a неравенство

2 – ax – x2

---------------------------- m 3 1 – x + x2

верно для всех значений переменной?

145

10. Найти множество значений a, при оторых существует хотя бы одно решение системы:

2x2 – (5a + 2)x + 2a2 – 2a – 4 m 0, а) x + a – 5 = 0;

2x2 + (a – 2)x m a2 + 2a; б) x + 2a – 1 = 0.

11. Найти все значения параметра p, при оторых неравенство

	x2 + p2	l 1 выполняется для всех x, удовлетворяющих условию
	p----(---x------+-----6---)

–1 < x < 1.

12.При а ом значении q площадь фи#уры, заданной на оординатной плос ости неравенством:

а) |x – y + 2| + |x + 2y – 1| m q, будет равна 96; б) |x + y + 2| + |2x – y – 2| m q, будет равна 6?

13.Найти множество значений a, при оторых уравнение имеет ровно три орня:

а) (2x2 – (3a – 6)x + a2 – 3a)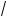5 + 4x – x2 = 0; б) (2x2 – (3a + 6)x + a2 + 3a)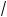x2 + x – 2 = 0; в) (3x2 – 2(2a – 3)x + a2 – 2a)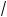2 + x – x2 = 0.

Ответы

1. a Ý [–3; 2) Ÿ (2; 6]. 2. а) a Ý (–×; 5]; б) a Ý (–0,12; +×); в) a − 3;

) a = 2. 3. а) Если a < 1, то x Ý		9	;	2a – 3		; если a Ý	1;	15	, то x Ý
		--		----------------				------
		8		a – 1				7

Ý	9	; +× ; если a >			15	, то x Ý	2a – 3	; +×		; б) если a Ý (–×; –10) Ÿ (2; +×),
	--				------		----------------
	8				7		a – 1
то x <			------------------------5(a – 2)	; если a Ý (–10; 2), то x >					------------------------5	(a – 2)	; если a = –10, то x Ý R;
			2(a + 10)						2(a + 10)

если a = 2, то x Ý ¾. 4. а) a Ý (6; +×); б) a Ý (–6; 6); в) a = 5; ) a Ý (0,5; 1).

5. a = –3. 6. a Ý (–1; 2). 7. a Ý

8 – 4

7 ; 0

Ÿ

2;

8 + 4 7

. 8. а) Если a < 0,

3

3

то x Ý

2a;

5------a

; если a = 0, то решений нет; если a > 0, то x Ý

5------a ; 2a

;

3

3

б) если a < 0, то x Ý (3a; a) Ÿ (–a; –2a); если a = 0, то решений нет; если a > 0, то x Ý (–2a; –a) Ÿ (a; 3a). 9. a Ý [–1; 7]. 10. а) a Ý [1; 4]; б) a Ý [0; 1].

11. p Ý		7 + 3	5 ; +×	. 12. а) q = 12; б) q = 3. 13. а) a Ý (–2; 2] Ÿ {6} Ÿ [8; 10);
		2

б) a Ý {–6} Ÿ [–5; –4) Ÿ (–2; 2]; в) a Ý (–3; 1] Ÿ {3} Ÿ [4; 6).

146

Тема 8

1.Применение теоремы Виета определению зна ов орнейвадратно(о трехчлена

2.Расположение орней вадратно(о трехчлена

СПРАВОЧНЫЙ МАТЕРИАЛ

1.Применение теоремы Виета определению зна ов орнейвадратно(о трехчлена

1°. Ка известно, между орнями x1 и x2 вадратно#о трехчле-

на ax2 + bx + c и е#о оэффициентами a, b, c справедливы следующие соотношения (теорема Виета):

x1 + x2	b	, x1x2	c
	= –--		= -- .
	a		a

С помощью этих соотношений можно исследовать зна и орней вадратно#о трехчлена.

2°. Т е о р е м а 1. Чтобы орни вадратно о уравнения (трехчлена) были действительными и имели одина овые зна и, необходимо и достаточно выполнение соотношений:

D = b2 – 4ac l 0; x	x		c	> 0.
		2	= --
1			a

При этом оба орня будут положительными, если дополнительно выполняется условие

b

x1 + x2 = –-- > 0, a

и оба орня будут отрицательными, если выполняется условие

b

x1 + x2 = –-- < 0. a

147

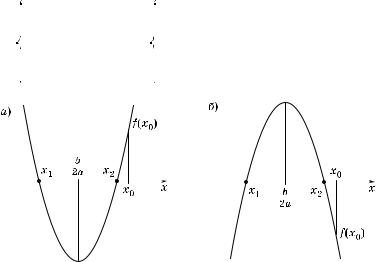
3°. Т е о р е м а 2. Чтобы орни вадратно о уравнения (трехчлена) были действительными и имели различные зна и, необходимо и достаточно выполнение соотношений:

	D = b2	– 4ac > 0, x	x		c	< 0.
				2	= --
		1			a
При этом отрицательный орень будет иметь меньшую абсо-
		b
лютную величину, если x1 + x2 = –-- > 0.
		a
Если же x1	b	< 0, то отрицательный орень будет иметь
	+ x2 = –--
	a

бQольшую абсолютную величину.

2. Расположение орней вадратно(о трехчлена

1°. При решении мно#их задач требуется знание дру#их важных теорем и их следствий о расположении орней вадратно#о трехчлена на оординатной прямой.

2°. Пусть вадратный трехчлен f(x) = ax2 + bx + c имеет действительные орни x1 и x2 (#де x1 < x2), а x0 — а ое-нибудь действительное число.

3°. Т е о р е м а 1. Чтобы оба орня вадратно о трехчлена были меньше, чем число x0 (т. е. лежали на оординатной прямой левее, чем точ а x0), необходимо и достаточно выполнение

условий (рис. 39, а и б):

a > 0,

a < 0,

D l 0,

D l 0,

а)

b

, или б)

b

,

–------

< x

–------ < x

2a

0

2a

0

f(x0) > 0

f(x0) < 0.

Рис. 39

148

4°. Т е о р е м а 2. Чтобы оба орня вадратно о трехчлена были больше, чем число x0 (т. е. лежали на оординатной прямой правее, чем точ а x0), необходимо и достаточно выполнение условий (рис. 40, а и б):

		a > 0,				a < 0,
		D l 0,				D l 0,
а)		b		, или б)		b
		–------	> x			–------	> x	,
		2a	0			2a	0
		f(x0) > 0				f(x0) < 0.

Рис. 40

5°. Т е о р е м а 3. Чтобы один из орней вадратно о трехчлена был меньше, чем число x0, а дру ой больше, чем число x0

(т. е. точ а x0 лежала бы между орнями), необходимо и достаточно выполнение условий (рис. 41, а и б):

	a > 0,		a < 0,
а)	f(x	) < 0 или б)	f(x ) > 0.
	0		0

Рис. 41

149

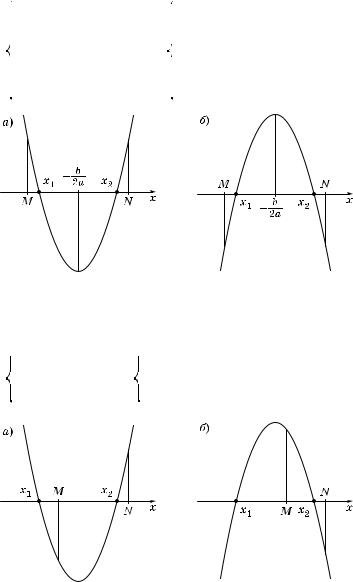
6°. С л е д с т в и е 1. Чтобы оба орня вадратно о трехчлена были больше, чем число M, но меньше, чем число N (M < N), т. е. лежали в интервале (M; N), необходимо и достаточно выполнение условий (рис. 42, а и б):

		a > 0,					a < 0,
		D l 0,					D l 0,
а)		M < –	b	< N,	или б)		M < –	b	< N,
			------					------
			2a					2a
		f(M) > 0,					f(M) < 0,
		f(N) > 0					f(N) < 0.

Рис. 42

7°. С л е д с т в и е 2. Чтобы толь о больший орень вадратно о трехчлена лежал в интервале (M; N), необходимо и достаточно выполнение условий (рис. 43, а и б):

a > 0,	a < 0,
а) f(M) < 0, или б)	f(M) > 0,
f(N) > 0	f(N) < 0.

Рис. 43

150