Задачи с параметрами и методы их решения

12. При а их значениях a неравенство 4x2 – 9ax + 2a2 < 0 выполняется для всех x та их, что |x – 3| m 1?

1.Сначала решим неравенство |x – 3| m 1, т. е. –1 m x – 3 m 1, от уда x Ý [2; 4].

2.Рассмотрим фун цию

f(x) = 4x2 – 9ax + 2a2.

(1)

3. Чтобы фун ция (1) была отрицательной на отрез е [2; 4], достаточно выполнения условий

f(2) m 0,	или		16 – 18a + 2a2 m 0,	или		1 m a m 8,	(2)
f(4) m 0,			64 – 36a + 2a2 m 0,			2 m a m 16.

4.Решив систему (2), находим 2 m a m 8.

5.Ответ: a Ý [2; 8].

13.При а их значениях k один из орней уравнения

(k – 2)x2 – 2(k + 3)x + 4k = 0

(1)

больше 3, а дру#ой меньше 2?

1. Со#ласно следствию 4 из п. 2, имеем сово упность двух систем неравенств:

a > 0, а) f(2) < 0,

f(3) < 0;

a < 0, б) f(2) > 0,

f(3) > 0.

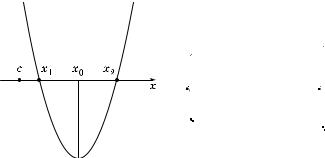
2. Система а) в данном случае имеет вид

k – 2 > 0,

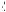f(2) = (k – 2) · 4 – 2(k + 3) · 2 + 4k < 0, f(3) = (k – 2) · 9 – 2(k + 3) · 3 + 4k < 0,

от уда 2 < k < 5.

3.Система б) не имеет решений.

4.Ответ: k Ý (2; 5).

14.При а их значениях параметра a абсолютная величина одно- #о из орней уравнения

a2x2 + ax – 2 = 0

больше 1, а дру#о#о меньше 1?

161

1. Задача равносильна следующей: при а их значениях параметра a один из двух орней вадратно#о трехчлена

f(x) = a2x2 + ax – 2

(1)

принадлежит интервалу (–1; 1), а второй расположен вне это#о интервала и по модулю не равен 1?

2. Заметим, что ровно один орень трехчлена (1) принадлежит интервалу (–1; 1) толь о то#да, о#да числа f(–1) и f(1) имеют разные зна и ( орни по модулю не равны 1). Поэтому требование задачи выполняется толь о при условии f(–1)f(1) < 0, оторое в данном случае примет вид

(a2 – a – 2)(a2 + a – 2) < 0.

(2)

3.Решив неравенство (2), находим, что –2 < a < –1 или 1 < a < 2.

4.Ответ: a Ý (–2; –1) Ÿ (1; 2).

15.Найти все значения c, при оторых орни уравнения x2 + x + + c = 0 действительны и оба больше c.

1.Если оба орня вадратно#о трехчлена y = x2 + x + c больше c, то е#о #рафи имеет вид, изображенный на рис. 51.

2.Та им образом, должны выполняться условия теоремы 2 из

п. 2:

а) парабола y = x2 + x + c пересе ает ось Ox в двух точ ах, т. е. D > 0, #де D = 1 – 4c;

b

б) абсцисса вершины параболы x0 = –------ находится правее точ-

2a

1

и c, т. е. –-- > c;

2

в) значение трехчлена y = x2 + x + c в точ е x = c положительно, т. е. y(c) > 0, #де y(c) = c2 + c + c = c2 + 2c.

3. В результате приходим системе неравенств

		1 – 4c > 0,		1	,
				c < --
		1		4
			т. е.		1
		c < –-- ,
		2		c < –	--	,
		c(c + 2) > 0,			2
				c < –2; c > 0.
		Решением этой системы является
	промежуто c < –2.
Рис. 51		4. Ответ: c Ý (–×;–2).

162

16. При а их значениях a оба орня вадратно#о трехчлена (2 – a)x2 – 3ax + 2a

1

действительны и больше -- ?

2

1.	Используя теорему 2 из п. 2, получим сово упность двух сис-
тем неравенств:
			2 – a > 0,								2 – a < 0,
			9a2 – 8a(2 – a) l 0,								9a2 – 8a(2 – a) l 0,
а)				3a	1	,			б)			3a	1
	--------------------- >				--					--------------------- >			-- ,
			2	(2 – a)	2						2	(2 – a)	2
			1			1		+ 2a > 0;			1		1	+ 2a < 0.
			--	(2 – a) – 3a · --							--	(2 – a) – 3a · --
			4			2					4		2
2.	Решив систему (а), находим								16	m a < 2; система (б) не имеет
									------
									17
решений.
3.	Ответ: a Ý						16
							------ ; 2 .
							17

17. При а их значениях k неравенство

(k – 1)x2 + (2k – 3)x + k – 3 > 0 (1) выполняется хотя бы для одно#о значения x < 1?

1.Пусть k > 1. Положим f(x) = (k – 1)x2 + (2k – 3)x + k – 3. То#да, а видно из рис. 52, а—в, все#да найдется хотя бы одно значение x < 1, при отором неравенство f(x) > 0 верно.

2.Пусть k = 1. То#да неравенство (1) примет вид –x – 2 > 0. Оно верно при x < –2. Значит, k = 1 удовлетворяет условию задачи.

Рис. 52

163

Рис. 53

3. Пусть k < 1. На рис. 53, а—в изображены #рафи и фун ции f(x) при D > 0, D = 0 и D < 0. Условию задачи удовлетворяет толь о случай а). Со#ласно теореме 1 из п. 2, получим систему

	k – 1 < 0,						k < 1,
	D > 0,						(2k – 3)2 – 4(k – 3)(k – 1) > 0,
	b	т. е.					3 – 2k
	–------ < 1,						-------------------- < 1,
	2a						2(k – 1)
	f(1) < 0,						k – 1 + 2k – 3 + k – 3 < 0.
			3	< k < 1.
Решив ее, находим --
			4
4. Ответ: k Ý		3	; +×				.
		--
		4
18. Найти все значения k, при оторых неравенство
			kx2 – 4x + 3k + 1 > 0					(1)

выполняется для всех x > 0.

1. Понятно, что значения k должны быть положительны, таа в противном случае все#да найдутся та ие x > 0, для оторых фун ция y = kx2 – 4x + 3k + 1 принимает отрицательные значения (при k < 0 ветви параболы направлены вниз; случай k = 0 та же не подходит).

2. При k > 0 возможны два случая, удовлетворяющие условию задачи.

а) Квадратный трехчлен не имеет действительных орней, если

k > 0,

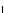16 – 4k(3k + 1) < 0.

164

Решив эту систему, получим k > 1.

В этом случае неравенство (1) выполняется для всех x.

б) Корни вадратно#о трехчлена действительны, но оба меньше или равны нулю: x1 m 0, x2 m 0.

Со#ласно теореме 1 из п. 2, составим систему

k > 0, D l 0,

2

-- m 0, k

3k + 1 l 0,

оторая несовместна. Та им образом, случай а) исчерпывает все решения задачи.

3.Ответ: k Ý (1; +×).

19.Найти все значения k, при оторых из неравенства

kx2 – x + 1 – k < 0	(1)
следует неравенство
0 < x < 1.	(2)

1. Прежде все#о отметим, что одно неравенство является следствием дру#о#о, если множество решений перво#о неравенства цели ом содержит множество решений второ#о. Например, если x удовлетворяет неравенству |x| < 3, то x2 < 10, т. е. неравенство x2 < 10 есть следствие неравенства |x| < 3. В самом деле, множество

решений (–10 ; 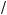10 ) неравенства x2 < 10 цели ом содержит множество решений (–3; 3) неравенства |x| < 3.

2.Со#ласно условию, требуется найти все значения k, при оторых любое число x, удовлетворяющее неравенству (1), удовлетворяет и неравенству (2).

3.Это означает, что неравенство (1) достаточно для выполнения неравенства (2), а неравенство (2) необходимо для выполнения неравенства (1).

4.По ажем, что число k должно быть положительным.

а) Если k < 0, то вадратное неравенство (1) выполняется либо при всех x (рис. 54, а), либо при тех x, оторые лежат вне отрез а,

165

Рис. 54

содержаще#о орни вадратно#о уравнения kx2 – x + 1 – k = 0 (рис. 54, б).

б) В аждом из рассмотренных случаев обязательно найдутся значения x, удовлетворяющие условию (1), но не удовлетворяющие условию (2), т. е. в этих случаях условие (2) не является необходимым для выполнения условия (1).

в) Если k = 0, то из неравенства (1) следует, что x > 1, а это противоречит неравенству (2).

5.Ита , k > 0. Та а D = 1 – 4k(1 – k) = (1 – 2k)2 l 0 при любых k, то решения неравенства (1) за лючены между орнямивадратно#о трехчлена.

6.В результате приходим следующим выводам:

а) чтобы выполнялись требования задачи, нужно, чтобы орнивадратно#о трехчлена принадлежали отрез у [0; 1] (см. решение задачи 11);

б) последнее означает, что должны выполняться требования следствия 1 из п. 2.

7. Составим систему уравнений

k > 0,

D = (1 – 2k)2 > 0,

1

0 < ------ < 1,

2k

f(0) = 1 – k l 0,

f(1) = k – 1 + 1 – k l 0,

1

от уда находим -- < k m 1.

2

8. Ответ: k Ý 1--2 ; 1 .

166

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. Решить уравнение

(k – 1)x2 – (2k – 1)x + k + 5 = 0.

Исследовать зна и орней в зависимости от k.

2. Установить, при а их значениях параметра k уравнение: а) (k – 2)x2 + (2k – 3)x + k2 – 3k + 2 = 0 имеет два орня, один из

оторых меньше (–1), а дру#ой больше (–1);

б) x2 + (2k – 1)x + k2 – 6k + 8 = 0 имеет орни разных зна ов; в) kx2 – (3k + 2)x + 2(k + 1) = 0 имеет орень, больший, чем 1. 3. Установить, при а их значениях параметра k орни урав-

нения:

а) (k – 1)x2 – 2(k + 2)x + k + 13 = 0 больше 2; б) x2 – 4kx + 3 = 0 положительны;

в) kx2 – 2(k – 1)x + 3k – 2 = 0 отрицательны; #) x2 + 2x + k = 0 больше k;

д) (k + 2)x2 + (k – 1)x – k = 0 удовлетворяют условиям x1 < 1, x2 > 3;

е) x2 – (2k – 2)x + k2 – 2k – 3 = 0 удовлетворяют условиям –3 < < x1 < –1, 1 < x2 < 3;

ж) x2 – (3k – 2)x + 2k2 – k – 3 = 0 находятся между орнями уравнения x2 – (5k – 1)x + 6k2 – k – 2 = 0.

4.При а их k любое решение уравнения (k – 1)x2 – 2(k + 1)x +

+k – 3 = 0 удовлетворяет условиям –1 < x < 5?

5.При а их k толь о один орень уравнения x2 + kx + 4 = 0 удовлетворяет условиям – 3 < x < –1?

6.Найти все значения параметра a, при оторых заданное уравнение имеет решение на у азанном интервале:

а) x2 + 2ax + 7a – 12 = 0; (–×; 0); б) x2 – 2ax + 8a – 15 = 0; (1; +×); в) x2 + 2ax + 6a – 8 = 0; (–×; –1).

7.Найти все значения k, при оторых вадратный трехчлен x2 + (2k – 15)x + 7k – k2 отрицателен для всех значений x, удовлетворяющих неравенству 1 < x < 2.

8.Найти все значения параметра a, при оторых уравнение

ax2 – (a + 5)x – 6a + 35 = 0 имеет два различных орня, причем меньший из них принадлежит отрез у [–1; 8].

167

9. При а их значениях параметра a все решения неравенства (a – 1)x2 + 4ax + 3a > 0 являются та же решениями неравенства x2 – 2x – 3 < 0?

10. Дано неравенство x2 – (3a + 1)x + a > 0. Требуется установить, при а их значениях a:

а) это неравенство выполняется для всех x > 1; б) из это#о неравенства следует неравенство x > 1.

Ответы

1. Если k < 1 или 1 < k <						21------		, то x1, 2 = 2-----------------------------------------------------k – 1 ä 21 – 20k							; если k = 1, то
						20							2(k – 1)
x = 6; если k = 21------				, то x = 11; если k > 21------								, то орней нет; x1 > 0, x2 > 0 при
			20							20
k < –5 или 1 < k <				21------ ; x < 0, x			2	> 0 при –5 < k < 1. 2. а) k Ý (–×; 1) Ÿ (2; 3);
				20	1
б) k Ý (2; 4); в) k Ý (–×; –2) Ÿ (0; +×). 3. а) k Ý														1; 17------ ; б) k Ý ------		3- ; +× ;
														8		2
в) k Ý	2	1	; ) k Ý (–×;			–3); д) k Ý						–2; –	15	; е) k Ý (0; 2); ж) k Ý ¾.
	-- ;	-------											------
	3	2											11
4. k Ý 19------		; +×		Ÿ {1}. 5. k		Ý			13------	; 5	Ÿ {4}. 6. а) a Ý ( 12------				; 3] Ÿ [4; +×);
	8								3					7
б) a Ý ( 7-- ; 3] Ÿ [5; +×); в) a Ý ( 7--									; 2] Ÿ [4; +×). 7. k Ý (–×; 2) Ÿ							11-----------------------+	17 ;
3							4									2

+× . 8. a Ý (0; 0,1] Ÿ (5; 10]. 9. a Ý (–×; –3]. 10. а) a Ý (–×; 0); б) a Ý ¾.

168

Тема 9

1.Числовая последовательность

2.Арифметичес ая про(рессия

3.Геометричес ая про(рессия

4.С мма бес онечной (еометричес ой про(рессии при |q| < 1

СПРАВОЧНЫЙ МАТЕРИАЛ

1. Числовая последовательность

1°. Бес онечной числовой последовательностью называют фун цию, определенную на множестве натуральных чисел.

2°. Числовую последовательность принято обозначать (xn), #де n Ý N.

3°. Последовательность (xn) называют о раниченной, если существуют два числа m и M та ие, что для любо#о n Ý N справедливы неравенства m m xn m M.

4°. Последовательность (xn) называют возрастающей, если аждый ее член, начиная со второ#о, больше предыдуще#о, т. е. если xn + 1 > xn для всех натуральных n.

5°. Последовательность (xn) называют бывающей, если аждый ее член, начиная со второ#о, меньше предыдуще#о, т. е. если xn + 1 < xn для всех натуральных n.

2. Арифметичес ая про(рессия

1°. Числовую последовательность, аждый член оторой, начиная со второ#о, равен предшествующему члену, сложенному с одним и тем же числом, называют арифметичес ой про рессией. Обозначение: ò a1, a2, a3, ... an, ... .

2°. Из определения арифметичес ой про#рессии следует, что разность между любым ее членом и ему предшествующим равна

169

одному и тому же числу, т. е. a2 – a1 = a3 – a2 = ... = an – an – 1 = ... .

Это число называют разностью арифметичес ой про#рессии и обозначают бу вой d.

3°. Для то#о чтобы задать арифметичес ую про#рессию (an), достаточно знать ее первый член a1 и разность d.

4°. Арифметичес ая про#рессия является:

а) возрастающей, если ее разность — положительное число; б) убывающей, если ее разность — отрицательное число;

в) постоянной (все ее члены равны между собой), если ее разность равна нулю.

5°. Хара теристичес ое свойство арифметичес ой про рессии. Последовательность (an) является арифметичес ой про#рессией то#да и толь о то#да, о#да любой ее член, начиная со второ#о, есть среднее арифметичес ое предшествующе#о и последующе#о членов, т. е.

a	an	+ an + 2	, #де n Ý N.	(1)
	= ---------	----2-------------
n + 1

6°. Формула n-#о члена арифметичес ой про#рессии имеет вид

an = a1 + d(n – 1).

(2)

7°. Формула суммы n первых членов арифметичес ой про#рессии имеет вид

Sn	=	a----1-----+----a----n-	n	(3)
		2
или
Sn =	2----a-------+----d---(----n----–-------1--) n.			(4)
		2

8°. Из определения разности арифметичес ой про#рессии следует, что a1 + an = a2 + an – 1 = ... , т. е. сумма членов, равноотстоящих от онцов про#рессии, есть величина постоянная.

3. Геометричес ая про(рессия

1°. Числовую последовательность, первый член оторой отличен от нуля, а аждый член, начиная со второ#о, равен предшествующему члену, умноженному на одно и то же не равное нулю число, называют еометричес ой про рессией. Обозначение: –:: b1, b2, b3, ... , bn, ... .

170