Задачи с параметрами и методы их решения

1.Уравнение (1) имеет смысл при a − 0; значения x должны удовлетворять условиям cos 2x − 0, tg 2x − 0,5.

2.Разделив числитель и знаменатель дроби в левой части урав-

нения (1) на cos2 2x, а первой дроби в правой части на cos 2x, получим уравнение

	2 tg2 2x – 6a tg 2x – 11	=	2(2a + 1)		–	1	.	(2)
	---------------a---(----2----tg-------2----x-----–------1---)--------------		1-------	–----2----tg-------2----x--		a--

3. Пусть t = tg 2x. То#да после упрощения уравнения (2) оно примет вид

t2 – (3a – 1)t + 2a2 + a – 6 = 0.

(3)

Уравнение (3) имеет два орня t1 = a + 2 и t2 = 2a – 3.

4. Ранее было отмечено, что значения x должны удовлетворять условию tg 2x − 0,5. Поэтому необходимо ис лючить те значения a, при оторых t1 или t2 (или оба числа) равны 0,5. Имеем:

а) t1 = a + 2 = 0,5, от уда a = –1,5; при этом t2 = –6; б) t2 = 2a – 3 = 0,5, от уда a = 1,75; при этом t1 = 3,75.

5.	1	π n	, n Ý Z;
	Ответ: если a = –1,5, то x = --	arctg (–6) + ------
	2	2
	1	πk
	если a = 1,75, то x = --	arctg 3,75 + ------ , k Ý Z;
	2	2

если a − –1,5, a − 1,75, a − 0, то

1	πm
x = --	arctg (2a – 3) + -------- , m Ý Z;
2	2

1	π l	, l Ý Z.
x = --	arctg (a + 2) + -----
2	2

18. В зависимости от значений параметра a решить уравнение

--a-----sin--------x-------–----2-	=	a-----cos-----------x------–----2- .	(1)
a – 2 cos x		a – 2 sin x

1. Перейдем от дробно#о уравнения (1) целому с учетом ОДЗ. При условиях a – 2 cos x − 0 и a – 2 sin x − 0 получим равносильное уравнение

(sin x – cos x)(a2 – 2a(sin x + cos x) + 4) = 0.

(2)

2. Уравнение (2) сводится сово упности уравнений:

π	+ πn, n Ý Z, независимо от a;
а) sin x – cos x = 0, x = --
4

211

б) sin x + cos x =

a2 + 4

, или

---------------

2a

cos

π

=

a2 + 4

(3)

x – --

--------------- .

4

2 2a

3. Рассмотрим модуль правой части уравнения (3):

a2

+ 4

=

1

a

2

2

=

2

---------------

-------

--

+ --

l -------

1

2

2a

2

2

a

2

(та а

l 2). Поэтому уравнение (3) не имеет орней.

z + --

z

π

+ πn, n Ý Z, — орни уравне-

4. В п. 2 мы установили, что x = --

4

ния (2) (не зависящие от параметра a). Одна о из множества орней

π		следует отбросить те орни, при оторых a – 2 cos x = 0
--	+ πn
4
					a	, sin x	a
и a – 2 sin x = 0, или cos x = --							= -- .
					2		2
	5. Представим множество					π
						-- + πn а объединение двух мно-
						4
	π			5π
жеств: --		+ 2πk	и	------	+ 2πk , k Ý Z.
	4			4
		π	+ 2πk, то cos x =				2	a	при a =	2 .
	а) Если x = --						-------	и cos x = --
		4					2	2
Значит, при a =						π
			2 орни x = -- + 2πk — посторонние.
						4
		5π					2	a	при a = –	2 .
	б) Если x = ------		+ 2πk, то cos x = –-------					и cos x = --
		4					2	2
Значит, при a = –						5π
			2 орни x = ------ + 2πk — посторонние.
						4
	6. К этим же выводам приводит и условие a – 2 sin x = 0, та
		π
а при x = -- + 2πn имеем sin x = cos x.
		4
	7. Ответ: если a − –					π
					2 , то x = -- + 2πk;
						4
						5π	+ 2πk;
		если a − 2 , то x = ------
						4
		если a − ä 2 , то x =					π	πn, n, k Ý Z.
							-- +
							4

212

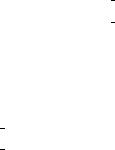
19. При а их значениях параметра a уравнение

sin2 3x – (a + 0,5) sin 3x + 0,5a = 0

(1)

имеет ровно три орня, принадлежащие отрез у

2π

?

------ ; π

3

1. Решив уравнение (1) а вадратное относительно sin 3x,

получаем, что оно равносильно сово упности двух уравнений:

sin 3x = 0,5;

(2)

sin 3x = a.

(3)

2. Уравнение (2) на отрез е

2π

имеет два орня: x

=

13π

------ ; π

1

----------

3

18

17π

иx2 = ---------- .

18

3.Следовательно, значение параметра a удовлетворяет требованию задачи, если уравнение (3) на данном отрез е имеет одинорень.

4. Фун ция y = sin 3x на отрез е		2π		принимает все зна-
		------ ; π
		3

чения от 0 до 1, причем аждое из этих значений, за ис лючением 1, — дважды. Поэтому требование задачи будет выполнено толь о при значении a = 1.

5.Ответ: a = 1.

20.При а их положительных значениях параметра a неотрицательные значения x, удовлетворяющие уравнению

cos (5a – 9)x = cos (9a + 17)x

(1)

и расположенные в поряд е возрастания, образуют бес онечную арифметичес ую про#рессию?

1. Приведем уравнение (1) виду

sin (7a + 4)x sin (2a + 13)x = 0.

2. Та а по условию a > 0, то 7a + 4 − 0, 2a + 13 − 0 и неотрицательные решения исходно#о уравнения задаются двумя сериями:

x =	-------π--k-------	, #де k Ý Z, k l 0;	(2)
	7a + 4
x =	πn	, #де n Ý Z, n l 0.	(3)
	2----a-----+------13-----

213

3. Здесь аждое из соотношений (2) и (3) образует бес онечную арифметичес ую про#рессию с первым членом, равным нулю, и раз-

ностями d1 =	π	и d2 =	π	соответственно.
	7----a-----+------4-		2----a-----+------13-----

4. Эти две арифметичес ие про#рессии образуют одну бес онечную арифметичес ую про#рессию при условии, что хотя бы одно из

чисел d----1-	или d----2-	является натуральным.
d2	d1
5. Рассмотрим случай, о#да
	d1	=	2a + 13	= p, #де p — натуральное.
	-----		--7-----a----+-----4----
	d2

Отсюда находим a = 4----p-----–------13----	> 0. Из это#о неравенства следует,
2 – 7p
		9	;	5	;	1
что p Ý {1; 2; 3}, и, значит, a Ý		--		------		------	.
		5		12		19
6. Рассмотрим случай, о#да

d2	=		7a + 4			= q, #де q — натуральное.
-----		2----a-----+------13-----
d1
Отсюда находим a =					4-------–----13-------q-				> 0. Здесь та же о азывается, что
					2q – 7
										9	22	; 35
q Ý {1; 2; 3} и, следовательно, a Ý -- ;											------		.
										5	3
7. Ответ: a			1	;	5	;	9	;	22	; 35
	Ý		19------		12------		5--		--3----		.

21. При а их целых отрицательных n фун ция

25x f(x) = cos 7nx sin ----------

n2

является периодичес ой с периодом T = 7π?

1. Та а по условию при любом значении x должно выполняться равенство

π 25x π

cos 7n(x + 7 ) · sin ---------- (x + 7 ) = cos 7nx · sin n2

то оно будет выполняться и при x = 0.

25x	,	(1)
----------
n2

214

2. При x = 0 получим
cos 7n(0 + 7π) · sin 25------	(0 + 7π) = cos 49πn · sin 175-----------	π--	= 0.
n2	n2

3. Та а cos 49πn − 0 при целых отрицательных n, то должно выполняться равенство

sin 175-----------	π--	= 0.	(2)
n2

4. Равенство (2) имеет место, о#да

175-----------π--	= πk, т. е. 175---------	= k, #де k Ý Z.
n2	n2

5.Пос оль у нас интересуют толь о целые отрицательные n, простым перебором находим, что n Ý {–1; –5}.

6.Подставляя значения n = –1 и n = –5 в соотношение (2), убеждаемся, что в обоих случаях получается тождество.

7.Ответ: n Ý {–1; –5}.

22.В зависимости от значений параметров a и b решить уравнение

		tg x – 2a – tg x – 2b = 2.
1.	Пола#ая u =	tg x – 2a , v = tg x – 2b , u l 0, v l 0, получим
уравнение
				u – v = 2.	(1)
2.	Кроме то#о, имеем
	u2 – v2 = (tg x – 2a) – (tg x – 2b),
т. е.
				u2 – v2 = 2(b – a).	(2)
3.	Уравнения (1) и (2) образуют систему
				u – v = 2,
от уда находим v =		1		u2 – v2 = 2(b – a),
		-- (b – a – 2); та а v l 0, то b l a + 2.
		2

4. Вернемся обозначению v = 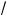tg x – 2b . Возведя обе части это#о равенства в вадрат, получим v2 = tg x – 2b, от уда

tg x = v	2	+ 2b, или tg x =	b – a – 2		2
			-----------2----------		+ 2b.

215

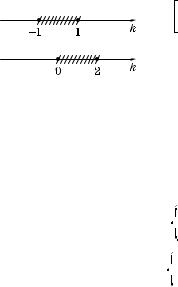
5. Ответ: если b – a l 2, то

x = arctg	b – a – 2		2	+ πk, k Ý Z;
	---------------------		+ 2b
	2
если b – a < 2, то орней нет.
23. При а их значениях параметра k уравнение
cos 2x + 2 sin x + 2k2 – 2k – 1 = 0				(1)

имеет хотя бы одно решение? Найти сумму та их целых значений k.

1. Та а cos 2x = 1 – 2 sin2 x, то уравнение (1) примет вид
1 – 2 sin2 x + 2 sin x + 2k2 – 2k – 1 = 0.	(2)
а) Пусть sin x = t, |t| m 1; то#да уравнение (2) запишется та :
t2 – t – k2 + k = 0.	(3)

б) Уравнение (3) имеет орни t1 = k и t2 = 1 – k.

в) Вернемся подстанов е t = sin x; имеем t1 = k = sin x, t2 =

=1 – k = sin x.

2.Уравнение (3) имеет хотя бы одно решение, если выполняется сово упность неравенств

|k| m 1,

|k – 1| m 1.

а) Из рис. 71 видно, что ис омыми целыми значениями k являются –1, 0, 1 и 2.

б) Сумма этих целых значений k рав-

Рис. 71	на 2.

3.Ответ: k Ý [–1; 2]; 2.

24.При а ой зависимости между параметрами a и b имеет решение уравнение sin ax sin bx = 1?

1.Исходное уравнение равносильно сово упности двух систем:

	sin ax = 1,	(1)
	sin bx = 1;
	sin ax = –1,	(2)
	sin bx = –1.

216

2. Для системы (1) имеем

ax =

--π

+ 2πk =

--π

(4k + 1), k Ý Z,

2

2

bx =

--π

+ 2πn =

--π

(4n + 1), n Ý Z,

2

2

от уда следует, что a--

=

--

4---k------+----1- .

b

4n + 1

3. Для системы (2) имеем

ax = –

--π

+ 2πk =

--π

(4k – 1), k Ý Z,

2

2

bx = –

--π

+ 2πn =

--π

(4n – 1), n Ý Z,

2

2

a

=

4k – 1

.

и, значит, --

4-----n------–----1-

b

4. Ответ: a--

= --4-----k----+----1-

или a--

=

--

4---k------–----1-

, k, n Ý Z.

b

4n + 1

b

4n – 1

25. В зависимости от значений параметра a решить уравнение

|cos 2x| = |sin2 x – a|.

(1)

1. Та а обе части уравнения (1) неотрицательны, то после

возведения в вадрат получим равносильное уравнение

cos2 2x = sin4 x + a2 – 2a sin2 x.

(2)

2. Упростим уравнение (2):

cos

2

2x =

1 – cos 2x 2

– 2a

1 – cos 2x

2

,

----

-

--------2-------------

-------------2-------------

+ a

или

3 cos2 2x + 2(1 – 2a) cos 2x – (1 – 2a)2 = 0.

(3)

3. Уравнение (3) сводится следующей сово упности:

cos 2x = 2a – 1;

(4)

cos 2x = 1-------–----2----a- .

(5)

3

4. Решим уравнение (4). Здесь должно выполняться условие

|2a – 1| m 1, т. е. 0 m a m 1; имеем

x = ä

1--

arccos (2a – 1) + πn, n Ý Z.

2

217

1 – 2a

----------------

3

5. Решим уравнение (5). Здесь должно выполняться условие m 1, т. е. –1 m a m 2; имеем

1– 2a π

x = ä-- arccos ---------------- + k, k Ý Z.

2 3

6.Ответ: если a < –1 или a > 2, то орней нет; если –1 < a < 0 или 1 m a m 2, то

1 1 – 2a π

x = ä-- arccos ---------------- + k, k Ý

2 31

если 0 m a m 1, то x = ä			1--	arccos	1-------–----2----a-	+ πk,
			2		3
x = ä	1--	arccos (2a – 1) + πn, k, n Ý
	2

26. В зависимости от значений параметра a решить уравнение

4 3

|tg x + a ctg x| = ---------- .

3

Z;

Z.

(1)

π k

1. Допустимыми значениями переменной x являются все x − ------ ,

2

k Ý Z. При та их значениях x, пола#ая y = tg x, перепишем уравнение (1) в виде

										a			4	3				(2)
								y + --				= ---------- .
										y				3
2. Если a = 0, то y =						4				3
						ä---------- . При a − 0 уравнение (2) равносиль-
									3
но сово упности уравнений
						y2				4	3
									– ---------- y + a = 0,
										3								(3)
										4	3
						y2
									+ ---------- y + a = 0.
										3
3. Дис риминанты обоих уравнений сово упности (3) совпада-
ют и имеют вид D = 4				4		– a				. Поэтому если a >						4	, то уравнение (1)
				--												--
				3												3
не имеет решений.
4. Пусть D l 0. То#да, решив уравнения (3), находим
y		2	3					4		– a , y				2	3		4	(4)
	1, 2	= ---------- ä						--					3, 4	= –---------- ä			-- – a .
			3					3						3			3

218

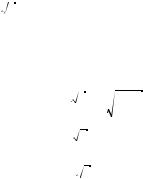
При a =	4	2	3
	--	имеем y = ä---------- . В остальных случаях все орни
	3		3

определяются формулами (4).

	4	, то
5. Ответ: если a < 0 или 0 < a < --
	3
		2	3	ä	4	+ πn, n Ý Z;
	x = arctg ä----------				-- – a
		3			3
		4	3	+ πk, k Ý Z;
если a = 0, то x = äarctg ----------
		3
4		2	3
если a = --	, то x = äarctg ---------- + πm, m Ý Z;
3		3
4	, то орней нет.
если a > --
3

27. Определить все значения параметра a, при оторых уравнение (a – 3) sin2 x + (a – 4) cos x + 1 = 0

имеет единственный орень в интервале		0;	π		, и у азать этот
			--
			2
орень.
1. Положим y = cos x, sin2 x = 1 – y2 и сведем три#онометриче-
с ое уравнение ал#ебраичес ому:
(a – 3)y2 – (a – 4)y + 2 – a = 0.					(1)

2.Требуется найти те значения a, при оторых уравнение (1) имеет единственный орень в интервале (0; 1).

3.Та ое требование реализуется в двух случаях:

а) уравнение (1) имеет единственный орень, оторый принадлежит интервалу (0; 1); это в свою очередь возможно либо при a – 3 = 0, либо при D = 0;

б) уравнение (1) имеет два орня, причем один из них принадлежит интервалу (0; 1), а дру#ой находится вне это#о интервала.

4. Рассмотрим по отдельности эти возможности.

а) При a = 3 уравнение (1) примет вид y – 1 = 0. То#да е#о орень y = 1 Ô (0; 1) и, значит, a = 3 не удовлетворяет у азанному требованию.

Та а D = (a – 4)2 + 4(a – 3)(a – 2) = 5a2 – 28a + 40 > 0 при любом a, т. е. случай D = 0 не имеет места.

219

б) Уравнение f(y) = 0 имеет единственный орень в интервале (0; 1), если f(0) · f(1) < 0. В данном случае

f(y) = (a – 3)y2 – (a – 4)y + 2 – a,

т. е. f(0) = 2 – a, f(1) = (a – 3) – (a – 4) + 2 – a = 3 – a. Ис омые значения a должны удовлетворять условию (2 – a)(3 – a) < 0, от у- да 2 < a < 3.

5. Ита , уравнение (1) имеет единственный орень в интервале (0; 1), если a Ý (2; 3). Найдем этот орень. Имеем

y1 =	a – 4 – 5a2 – 28a + 40	, y2 =	a – 4 + 5a2 – 28a + 40	.
	----------------------2----(---a----–----3-----)--------------------		----------------------2----(---a----–-----3----)---------------------

Та а 2 < a < 3, то y1 > 1, а y2 Ý (0; 1).

6. Из равенства cos x = y2 найдем соответствующий орень данно#о уравнения.

	7.	Ответ: a Ý (2; 3); x = arccos	a – 4 + 5a2		– 28a + 40	.
			----------------------2----	(---a----–-----3----)---------------------

28. Найти все пары чисел (a; b), для аждой из оторых при любом x справедливо равенство

a sin x + b = sin (ax + b).

(1)

1.Из условия следует, что равенство (1) должно выполняться,

вчастности, при x = 0.

2.При этом значении x получим равенство b = sin b, оторое справедливо толь о при b = 0, т. е. 0 = sin 0 = 0.

3.Подставив b = 0 в равенство (1), приходим уравнению

a sin x = sin ax,

оторое имеет решение при любом x толь о в тех случаях, о#да a Ý {–1; 0; 1}.

4.Ответ: (–1; 0); (0; 0); (1; 0).

29.Найти все пары чисел (a; b), для аждой из оторых при всех x справедливо равенство

a(cos x – 1) + b2 = cos (ax + b2) – 1.

(1)

1. Пусть (a; b) — пара чисел, удовлетворяющих условию задачи. Пос оль у данное равенство справедливо при любом x, в част-

220