Задачи с параметрами и методы их решения

Тема 6

1.Неравенства

2.Основные свойства неравенств

3.Действия с неравенствами

4.Решение линейных и вадратных неравенств

СПРАВОЧНЫЙ МАТЕРИАЛ 1. Неравенства

1°. Запись x l y (y m x) означает, что либо x > y, либо x = y, и читается та : «x больше или равно y» или «x не меньше y».

2°. Запись, в оторой два числа или два выражения, содержащие переменные, соединены зна ом >, <, l или m, называют неравенством.

3°. Неравенства, составленные с помощью зна ов > или <, называют стро ими; неравенства, составленные с помощью зна ов l

или m, — нестро ими.

4°. Два неравенства вида a > b и c > d называют неравенствами одина ово о смысла, а неравенства вида a > b, c < d — неравенствами противоположно о смысла.

5°. Вместо двух неравенств x < a, a < y употребляется запись x < a < y. Та ое неравенство называют двойным.

6°. Если неравенство представляет собой истинное выс азывание, то е#о называют верным.

7°. Неравенства, содержащие толь о числа, называют числовыми.

2. Основные свойства неравенств

1°. Если обеим частям верно#о неравенства прибавить одно и то же число, то получится верное неравенство, т. е. если a > b, то a + c > b + c.

81

2°. Если обе части верно#о неравенства умножить на одно и то же положительное число, то получится верное неравенство.

3°. Если обе части верно#о неравенства умножить на одно и то же отрицательное число и изменить зна неравенства на противоположный, то получится верное неравенство.

4°. Та а деление можно заменить умножением на число, обратное делителю, то анало#ичные правила справедливы и в отношении деления.

3. Действия с неравенствами

1°. Неравенства одина ово#о смысла можно почленно с лады-

вать. Например:
а)	a > b		б)	a < b
	+ c > d			+ c < n
	a + c > b + d;			a + c < b + n.
2°. Неравенства противоположно#о смысла можно почленно

вычитать, оставляя зна то#о неравенства, из оторо#о производится вычитание. Например,

a > b

– c < d

a – c > b – d.

3°. Неравенства одина ово#о смысла с положительными членами можно почленно умножать. Например, если a > b, то ak > bk, #де a > 0, b > 0, k Ý N.

Верно и обратное утверждение: если ak > bk, a > 0, b > 0, k Ý N, то a > b.

З а м е ч а н и е. Часто используют следующие важные неравенства:

a + b

а) ------------ l ab , если a l 0 и b l 0.

2

Это неравенство означает, что среднее арифметичес ое двух неотрицательных чисел не меньше их средне#о #еометричес о#о, причем равенство дости#ается толь о в том случае, о#да a = b.

a	b	l 2, если a > 0 и b > 0.
б) --	+ --
b	a

Это неравенство означает, что сумма двух взаимно обратных положительных чисел не меньше 2.

82

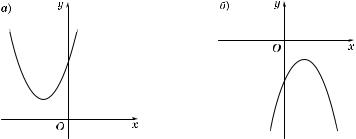
4. Решение линейных и вадратных неравенств

1°. Линейным неравенством называют неравенство вида ax + + b > 0 (или ax + b < 0).

а) Если a > 0, то неравенство ax + b > 0 равносильно неравенст-

b

ву x > –-- . a

б) Если a < 0, то неравенство ax + b > 0 равносильно неравенст-

b

ву x < –-- . a

2°. Квадратным неравенством называют неравенство вида ax2 + bx + c > 0 (или ax2 + bx + c < 0), #де a − 0.

3°. Два неравенства называют равносильными, если множества решений этих неравенств совпадают.

4°. Пусть требуется решить неравенство ax2 + bx + c > 0.

В зависимости от зна а дис риминанта D = b2 – 4ac возможны три случая:

а) Если D < 0, то #рафи вадратно#о трехчлена f(x) = ax2 + + bx + c не пересе ает ось Ox и лежит выше этой оси при a > 0 и ниже ее при a < 0. То#да при a > 0 множество решений неравенства есть вся числовая прямая (рис. 15, а), а при a < 0 оно является пустым (рис. 15, б).

б) Если D > 0, то #рафи вадратно#о трехчлена пересе ает ось Ox в точ ах x1 и x2 (x1 < x2), служащих орнями уравнения ax2 + + bx + c = 0. Эти точ и разбивают числовую прямую на три промежут а: (–×; x1), (x1; x2) и (x2; +×). При этом зна вадратно#о трехчлена совпадает со зна ом оэффициента a во всех точ ах про-

Рис. 15

83

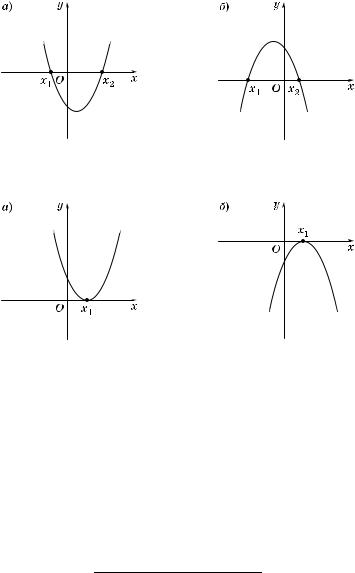
Рис. 16

Рис. 17

межут ов (–×; x1) и (x2; +×) и противоположен зна у оэффициента a во всех точ ах промежут а (x1; x2) (рис. 16, а и б).

в) Если D = 0, то #рафи вадратно#о трехчлена асается оси Ox в точ е x1, являющейся единственным орнем уравнения ax2 + + bx + c = 0. Точ а x1 разбивает числовую прямую на два промежут а: (–×; x1) и (x1; +×). Зна вадратно#о трехчлена совпадает со зна ом a при x − x1 (рис. 17, а и б).

ЗАДАЧИ С РЕШЕНИЯМИ

1. При а их значениях a неравенство

(x – a)(x – 2) m 0

имеет единственное решение?

84

1. Ле# о до#адаться, что если a = 2, то требование задачи удовлетворяется. Действительно, при a = 2 получаем неравенство

(x – 2)2 m 0,

имеющее единственное решение.

2.В случае, о#да a − 2, решением данно#о неравенства, очевидно, является отрезо .

3.Ответ: a = 2.

2.При а их значениях параметра m неравенство (m – 2)x2 – 2x + + m – 2 < 0 выполняется для всех x?

1.Пусть m − 2. То#да ветви параболы y = (m – 2)x2 – 2x + m – 2 должны быть направлены вниз и парабола не должна пересе ать ось Ox.

2.Для это#о необходимо, чтобы выполнялись условия

a < 0,	m – 2 < 0,

		D	< 0,	т. е.	1 – (m – 2)2 < 0.	(1)
		----
		4
3.	Решив систему неравенств (1), получим m < 1.
4.	Пусть m = 2. То#да данное неравенство примет вид –2x < 0,

т. е. оно выполняется толь о при x > 0. Поэтому значение m = 2 не удовлетворяет требованию задачи.

5. Ответ: m Ý (–×; 1).
3. Найти все значения a, для оторых выражение
(a2 – 1)x2 + 2(a – 1)x + 2	(1)
положительно при всех действительных значениях x.

1.Пусть a2 – 1 = 0, т. е. либо a = 1, либо a = –1. То#да в случае a = 1 выражение (1) равно 2 при всех x, а в случае a = –1 выражение (1) примет вид –4x + 2 и, значит, не будет положительным при всех x.

2.Пусть a2 – 1 − 0. То#да выражение (1) представляет собойвадратный трехчлен, оторый положителен при всех значениях x,

если оэффициент при x2 положителен, а дис риминант вадратно#о трехчлена отрицателен:

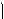a2 – 1 > 0,

D	= (a – 1)2	– 2(a2	(2)
----			– 1) < 0.
4

85

3. Система (2) равносильна следующей:

a2 – 1 > 0,	или		|a| > 1,
a2 + 2a – 3 > 0,			(a – 1)(a + 3) > 0,

от уда a > 1, a < –3.

4.Ответ: a Ý (–×; –3) Ÿ [1; +×).

4.При а их значениях параметра m #рафи и фун ций y = x2 + + m2 + 12 и y = 2(m + 2)x пересе аются в двух различных точ ах?

1.Графи и пересе утся в двух различных точ ах, если урав-

нение

x2 + m2 + 12 = 2 (m + 2)x

имеет два различных орня.

2. Преобразуем это уравнение виду

x2 – 2(m + 2)x + m2 + 12 = 0.

3. Та а D = (m + 2)2 – (m2 + 12) > 0, или m2 + 4m + 4 – m2 –

----

4

– 12 > 0, то m > 2.

4.Ответ: m Ý (2; +×).

5.При а их значениях параметра k #рафи и фун ций y = 2kx + 1 и y = (k – 6)x2 – 2 не пересе аются?

1.Графи и фун ций не пересе утся, если уравнение

	2kx + 1	= (k – 6)x2 – 2		(1)
не будет иметь орней.
2.	Преобразуем уравнение (1) виду
	(k – 6)x2 – 2kx – 3 = 0.			(2)
3.	Уравнение (2) не будет иметь орней, если		D	< 0, т. е. k2 +
			----
			4
+ 3(k – 6) < 0, от уда –6 < k <		3.

4.Ответ: k Ý (–6; 3).

6.В зависимости от значений параметра a решить неравенство

(a2 + a + 1)x – 3a > (2 + a)x + 5a.	(1)
1. После упрощения неравенство (1) примет вид
(a2 – 1)x > 8a.	(2)

86

2. а) Пусть |a| > 1; то#да неравенство (2) имеет решение x >

>	8a
	--------------- .
	a2 – 1
	б) Пусть |a| < 1; то#да неравенство (2) имеет решение x <	8a
		--------------- .
		a2 – 1
	в) Пусть a = 1; то#да неравенство (2) примет вид 0 · x > 8 и не
будет иметь решений.
	#) Пусть a = –1; то#да неравенство (2) примет вид 0 · x > –8
и будет выполняться при любом значении x.
	8a	;
	3. Ответ: если –× < a < –1 или 1 < a < +×, то x > ---------------
	a2 – 1
	8a
	если –1 < a < 1, то x < --------------- ;
	a2 – 1
	если a = –1, то x Ý R;
	если a = 1, то нет решений.
7. В зависимости от значений параметра a решить неравенство
	56x2 + ax – a2 < 0.	(1)
	1. Найдем дис риминант вадратно#о трехчлена: D = 225a2 l 0;

a a

орнями трехчлена являются x1 = –-- , x2 = -- .

7 8

a

2. При a > 0 неравенство (1) имеет решение –--

7

a

< x < -- .

8

a	a
3. При a < 0 неравенство (1) имеет решение --	< x < –-- .
8	7

4.	При a = 0 неравенство (1) не имеет решений.
5.		a	a	;
	Ответ: если a > 0, то –--		< x < --
		7	8
	a		a	;
	если a < 0, то --	< x < –--
	8		7

если a = 0, то нет решений.

8. Пусть x1 и x2 — действительные орни уравнения x2 – ax + a = 0, #де a — действительное число. Найти та ое значение a, чтобы ве-

личина выражения x21 + x22 была наименьшей.

1. Уравнение x2 – ax + a = 0 имеет действительные орни при условии неотрицательности е#о дис риминанта:

D = a2 – 4a l 0,

от уда

a m 0 и a l 4.

(1)

87

2. Требуется найти минимум неотрицательно#о выражения

y = x21 + x22 = (x1 + x2)2 – 2x1x2,

	оторое со#ласно теореме Виета мож-
	но записать в виде
	y = a2 – 2a.	(2)
	3. Та им образом, задача сводится
	отыс анию наименьше#о значения
	вадратно#о двучлена (2) в области (1)
	при условии y(a) l 0.
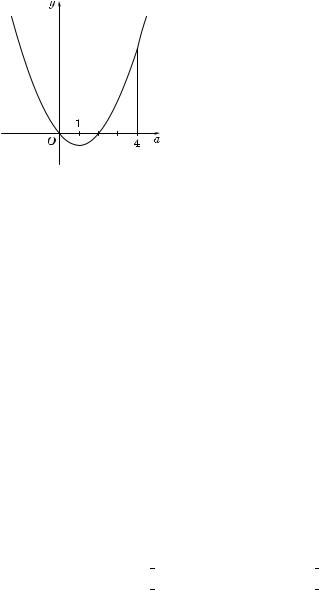
	4. Нетрудно установить (рис. 18),
	что вадратный двучлен (2) дости#ает
	наименьше#о значения на #ранице об-
	ласти (1), а именно при a = 0.
Рис. 18	5. Ответ: a = 0.

9. При а ом значении параметра t сумма вадратов орней уравнения

x2 + (2 – t)x – t2 + 1 = 0

(1)

принимает наименьшее значение?

1. Воспользуемся формулами Виета и выразим x21 + x22 через параметр t. Получим

f(t) = x21 + x22 = (x1 + x2)2 – 2x1x2 =

=(t – 2)2 – 2(–t2 + 1) = 3t2 – 4t + 2.

2.Если бы областью определения фун ции f(t) была вся числовая прямая, то наименьшее значение этой фун ции дости#алось

бы в точ е t =	2	(абсциссе вершины параболы), причем f		=
	--		наим
	3

=f 2 = 2 .

-- --

3 3

3.Одна о орни уравнения (1) существуют толь о в случае D l 0. Решив неравенство

D = (2 – t)2 + 4(t2 – 1) = 5t2 – 4t l 0,

получаем t Ý (–×; 0]	Ÿ		4	; +×		2	Ô (–×; 0] Ÿ		4	; +×	.
			--			и --			--
			5			3			5

88

а) На промежут е (–×; 0] фун ция f(t) убывает и принимает наименьшее значение при t = 0; f(0) = 2.

б) На промежут е			4			фун -
			-- ; +×
			5
ция f(t) возрастает и принимает наи-
меньшее значение при t =				4	f	4		=
				-- ;		--
				5		5
18
= ------ < 2 (рис. 19).
25
4. Ответ: t =	4
	-- .											Рис. 19
	5

10. При а их значениях параметра t наименьшее значение вадратно#о трехчлена

f(x) = 4x2 – 4tx + t2 – 2t + 2

(1)

на промежут е 0 m x m 2 равно 3?

1. При аждом фи сированном значении параметра t #рафи-ом вадратно#о трехчлена (1) является парабола, абсцисса верши-

t

ны оторой x = -- .

2

2. В зависимости от положения вершины параболы требуемые значения параметра t можно найти, рассматривая следующие три возможных случая:

	t			0 <		t	< 2,		t
		m 0,				--				l 2,
	--					2			--
а)	2		б)		t		в)		2
	f(0) = 3;						= 3;		f(2) = 3.
					--
				f	2

3. Решив аждую из этих трех систем с учетом то#о, что

f(0) = t2 – 2t + 2, f t = –2t + 2, f(2) = t2 – 10t + 18,

--2

за лючаем, что в первом случае t = 1 – 2 ; во втором t Ý ¾; в третьем t = 5 + 10 .

4. Ответ: t Ý (1 – 2 ; 5 + 10 ).

89

11. При а их значениях параметра a вершины парабол y = 4x2 + + 8ax – a и y = 4ax2 – 8x + a – 2 лежат по одну сторону от прямой y = –5?

1. Найдем оординаты вершин обеих парабол.

а) Абсцисса вершины первой из них x1 = –a, ее ордината y1 = = –4a2 – a.

1

б) Абсцисса вершины второй параболы x2 = -- , ее ордината y2 = a

4

= –-- + a – 2. a

2. Точ и A	(–a; –4a	2	– a) и A	1	4	+ a – 2		будут лежать по
				--	; –--
1				2 a	a

одну сторону от прямой y = –5 то#да и толь о то#да, о#да выполняется неравенство

(–4a

2

– a + 5)

4

+ a – 2 + 5

> 0,

–--

a

т. е.

(1 – a)

a +

5

a(a – 1)(a + 4) > 0,

--

4

или

a(a + 4)

a

5

(a

– 1)

2

< 0.

+ --

4

3. Решив это неравенство, получим ответ.

4. Ответ: a Ý (–×; –4)

Ÿ

5

; 0

.

–--

4

12.Решить уравнение |x – 3| = kx + 2.

1.Данное уравнение равносильно сово упности двух систем:

		x – 3 < 0,		x – 3 l 0,
а)		–x + 3 = kx + 2; б)		x – 3 = kx + 2.

2.Решим систему а). Имеем x < 3,

							1
			x = x	1	= ------------ .
						k	+ 1
	Определим значения k, при оторых x1 < 3. Из неравенства
1		< 3 находим k Ý (–×; –1) Ÿ				2	; +×		.
------------						–--
k +	1					3

90