
дополнительные вопросы алгебры(матанализа) / Задания к зачету (вычисление особого интеграла, задача о скачке)
.docxЗадания к зачету по спецкурсу.
Раздел 1. Вопросы по ТФКП.
1. Условие Коши-Римана (необходимое условие).
2. Интегральная теорема Коши.
3. Интегральная формула Коши.
4. Теорема Лиувилля.
Задачи к разделу 1.
1.1. Выполнить указанные действия:
1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 .
.
1.2. Найти модули и аргументы комплексных чисел:
1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 ;
5)
;
5)
 ;
6)
;
6)
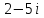 ;
7)
;
7)
 ;
8)
;
8)
 ;
;
1.4. Найти все значения следующих корней и построить их:
1)
 ;
2)
;
2)
 ;
3)
;
3)
 ;
4)
;
4)
 ;
5)
;
5)
 ;
6)
;
6)
 ;
6)
;
6)
 .
.
1.8(1)* Исходя из геометрических рассмотрений, доказать неравенство:
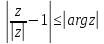 .
.
1.23. Выяснить геометрический смысл указанных соотношений:
 ;
;
 ;
;
 .
.
1.28. Выяснить геометрический смысл
соотношения:
 .
.
1.59. Представить в показательной форме числа:
 .
.
1.60. Найти
 .
.
1.61. Найти модули и главные значения аргументов комплексных чисел
 .
.
1.68. Найти действительные и мнимые части следующих значений функций:
1)
 ;
2)
;
2)
 ;
3)
;
3)
 .
.
1.109. Определить линию, заданную
уравнением
 .
.
1.110. Определить линию, заданную
уравнением
 .
.
1.111. Определить линию, заданную
уравнением
 .
.
1.121. Для отображения
 найти:
найти:
1) образы линий
 ;
2) прообразы линий
;
2) прообразы линий
 .
.
1.132. Найти постоянные
 ,
при которых функция
,
при которых функция
 будет аналитической.
будет аналитической.
Раздел 2. Интеграл Коши, интеграл типа Коши, особый интеграл.
1. Определение и свойства интеграла Коши.
2. Определение и свойства интеграла типа Коши.
3. Определение и свойства особого интеграла.
4. Основная лемма.
5. Формулы Сохоцкого.
6. Постановка краевой задачи Римана.
7. Решение задачи о скачке.
Задачи к разделу 2.
1. Вычислить интеграл типа Коши
 ,
взятый по контуру
,
взятый по контуру
 (
( ,
с плотностью
,
с плотностью
 ,
если:
,
если:
1)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
2)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
3)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
4)
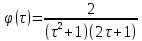 ,
,
 – единичная окружность
– единичная окружность
 ;
;
5)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
6)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
7)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
8)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
9)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
10)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
11)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
12)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
13)
 ,
,
 – единичная окружность
– единичная окружность
 .
.
2. Вычислить особый интеграл
 ,
взятый по контуру
,
взятый по контуру
 (
( ,
с плотностью
,
с плотностью
 ,
если:
,
если:
1)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
2)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
3)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
4)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
5)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
6)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
7)
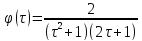 ,
,
 – единичная окружность
– единичная окружность
 ;
;
8)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
9)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
10)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
11)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
12)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
13)
 ,
,
 – единичная окружность
– единичная окружность
 .
.
3. Решить задачу Римана с краевым
условием
 при условии
при условии
 ,
считая, что:
,
считая, что:
1)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
2)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
3)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
4)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
5)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
6)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
7)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
8)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
9)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
10)
 ,
,
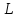 – единичная окружность
– единичная окружность
 ;
;
11)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
12)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
13)
 ,
,
 – единичная окружность
– единичная окружность
 ;
;
