Госы 5к Надя / fomin-a

В.И. ФОМИН

ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО

ТАМБОВ ♦ ИЗДАТЕЛЬСТВО ГОУ ВПО ТГТУ ♦

2010

УДК 517.53/.55(075.8) ББК В161.5я73

Ф762

Р е ц е н з е н т ы:

Доктор физико-математических наук, профессор, заведующий лабораторией компьютерных алгебраических вычислений ТГУ им. Г.Р. Державина

Г.И. Малашонок

Доктор физико-математических наук, профессор, заведующий кафедрой

«Распределённые вычислительные системы» ГОУ ВПО ТГТУ

С.М. Дзюба

Фомин, В.И.

Ф762 Теория функций комплексного переменного : учеб. пособие / В.И. Фомин. – Тамбов : Изд-во ГОУ ВПО ТГТУ, 2010. – 296 с. – 125 экз. – ISBN 978-5-8265-0909-8.

Изложен теоретический материал по дисциплине "Теория функций комплексного переменного", предусмотренный Государственным образовательным стандартом для специальности 090105. Теоретические положения иллюстрируются конкретными примерами и рисунками.

Предназначено для студентов второго курса инженерных специальностей вузов.

УДК 517.53/.55(075.8) ББК В161.5я73

ISBN 978-5-8265-0909-8	© Государственное образовательное учреждение
	высшего профессионального образования
	Тамбовский государственный технический
	университет (ГОУ ВПО ТГТУ), 2010

Министерство образования и науки Российской Федерации

Государственное образовательное учреждение высшего профессионального образования Тамбовский государственный технический университет

В.И. Фомин

ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО

Рекомендовано Учёным советом университета в качестве учебного пособия для студентов 2 курса

инженерных специальностей вузов

Тамбов Издательство ГОУ ВПО ТГТУ

2010

Учебное издание

ФОМИН Василий Ильич

ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО

Учебное пособие

Редактор З.Г. Ч е р н о в а Инженер по компьютерному макетированию М.Н. Р ы ж к о в а

Подписано в печать 01.04.2010 Формат 60 × 84 / 16. 17,2 усл. печ. л. Тираж 125 экз. Заказ № 204

Издательско-полиграфический центр ГОУ ВПО ТГТУ

392000, Тамбов, Советская, 106, к. 14

ВВЕДЕНИЕ

Вданном учебном пособии изложен теоретический материал по дисциплине "Теория функций комплексного переменного", предусмотренный Государственным образовательным стандартом высшего профессионального образования для студентов второго курса инженерных специальностей вузов.

Впараграфах 1 – 4 рассматриваются алгебраические операции над комплексными числами, расширенная комплексная плоскость, свойства числовых последовательностей и рядов с комплексными членами.

Впараграфах 5 – 9 вводятся понятия предела, непрерывности, дифференцируемости и аналитичности для функций комплексного переменного; изучаются свойства аналитических функций; рассматриваются основные элементарные функции.

Впараграфах 10 – 13 изучаются свойства интегралов функций комплексного переменного; доказываются интегральная теорема Коши для односвязной и многосвязной области, интегральная формула Коши, бесконечная дифференцируемость аналитической функции, принцип максимума модуля аналитической функции.

Впараграфах 14 – 18 излагаются свойства функциональных рядов с комплексными членами; находятся разложение аналитической в открытом круге функции в ряд Тейлора, разложение аналитической в кольце функции в ряд Лорана; изучается связь между типом изолированной особой точки функции и видом лорановского разложения этой функции в проколотой окрестности данной точки.

Учебное пособие снабжено необходимым справочным материалом: списком обозначений, биографическим

справочником и предметным указателем.

		ОБОЗНАЧЕНИЯ
:: =	–	оператор определения ("это по определению")
и	–	начало и конец доказательства
	–	предположение противного ("предположим
		противное")
	–	отрицание предположения противного
		("предположение противного неверно")
	–	знак логического следования ("следует", "вытекает")
	–	знак равносильности (эквивалентности) ("тогда и
		только тогда")
	–	квантор общности ("для любого", "для каждого",
		"для всякого")
	–	квантор существования ("существует", "найдётся")
	–	знак принадлежности ("принадлежит")

Îили – знак непринадлежности ("не принадлежит")

– конъюнкция ("и")

– дизъюнкция ("или")

| (или :)			– " такой (такая, такое), что"
Æ			–	пустое множество
{z1, z2 ,..., zn }или {zi }in=1 – конечное множество, состоящее из
				элементов z1 , z2 ,..., z n
{z | P(z)}			–	множество элементов z , удовлетворяющих условию
				P(z)
A Ì B			–	множество A включено во множество B и A ¹ B
A Í B			–	множество A включено во множество B (возможно,
A È B			–	что A = B )
				объединение множеств А и В
A Ç B			–	пересечение множеств А и В
A \ B			–	разность множеств А и В
			–	множество натуральных чисел
			–	множество целых чисел
			–	множество вещественных (действительных) чисел
+			–	множество неотрицательных вещественных
				(действительных) чисел
R −			–	множество отрицательных вещественных
				(действительных) чисел
R 2			–	множество всевозможных упорядоченных пар
				вещественных (действительных) чисел
C			–	поле комплексных чисел (комплексная плоскость)
			–
	C			расширенное множество комплексных чисел
				(расширенная комплексная плоскость)
i			–	мнимая единица
Re z			–	действительная часть комплексного числа z

Im z					–
					–
z
	z			(или ρ )	–
Arg z					–

arg z (или ϕ ) –

SR (z0 )						–
OR (z0 )						–
		R (z0 )				–
O
C \ OR (z0 )						–
C \ O					R (z0 )	–
Oε (a)						–
&			(a)			–
Oε
∞			(∞)			–
Oi						–
		E
	f (D)					–
p(w0 )						–
lim z n						–
n→∞
	lim f (z)					–
z→z0
	z					–
	w					–
sh z						–
ch z						–
th z						–
cth z						–
γ						–
ГD						–
ED						–
I Г						–
EГ						–
	f ′(z0 ) , w′(z0 ) ,
	f ′(z)					–
б.б.в.						–
б.м.в.						–

dw(z0 ) , df (z0 ) dw(z) , df (z)

dz
o( z)	–
∫ f (z)dz	–
γ

мнимая часть комплексного числа z комплексно сопряжённое числу z модуль комплексного числа z

аргумент комплексного числа z

главное значение аргумента комплексного числа z

окружность с центром в точке z0 радиуса R

открытый круг с центром в точке z0 радиуса R

замкнутый круг с центром в точке z0 радиуса R

внешность открытого круга OR (z0 )

внешность замкнутого круга OR (z0 )

ε-окрестность точки a

проколотая ε-окрестность точки a

несобственное комплексное число iE-окрестность несобственного комплексного

числа ∞

образ множества D при отображении f

полный прообраз точки w0 при заданном отображении предел последовательности {zn }

предел функции f (z) в точке z0

приращение независимого переменного z приращение функции w = f (z)

гиперболический синус z гиперболический косинус z гиперболический тангенс z гиперболический котангенс z ориентированная кривая с ориентацией,

соответствующей убыванию параметра кривой граница множества D

внешность множества D

внутренность замкнутой простой кривой Г внешность замкнутой простой кривой Г

df (z0 )

,

dw(z0 )

,

df

,

dw

– производная

dz

dz

dz

z = z0

dz

z = z0

функции w = f (z) в точке z0

производная функции f (z)

бесконечно большая величина

бесконечно малая величина

–

дифференциал функции w = f (z) в точке z0

–

дифференциал функции w = f (z)

–

дифференциал независимого переменного z

бесконечно малая величина высшего порядка

по сравнению с z	при	z → 0
интеграл функции	f (z)	вдоль кривой γ

∫ f ( z ) dz	–	контурный интеграл функции f (z) вдоль
γ
		положительно ориентированного контура γ
∫ f ( z ) dz	–	контурный интеграл функции f (z) вдоль
γ
		отрицательно ориентированного контура γ
res[ f (z); z0 ]	–	вычет функции f (z) относительно точки z0

1. КОМПЛЕКСНЫЕ ЧИСЛА

Понятие комплексного числа; операции сложения и умножения комплексных чисел, их свойства; алгебраическая форма записи комплексного числа; операции вычитания и деления комплексных чисел; модуль и аргумент комплексного числа; тригонометрическая форма записи комплексного числа; геометрическая интерпретация арифметических действий над комплексными числами; формула Муавра; извлечение корня натуральной степени из комплексного числа.

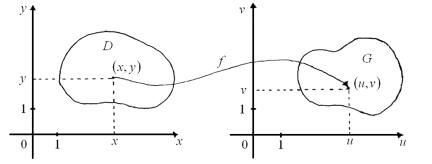
При исследовании различных физических процессов, например, при решении задач гидродинамики и газовой динамики [1.1, с. 309], приходится рассматривать преобразования плоских областей, т.е. изучать отображения вида

f : D Í R 2 ® G Í R 2 ,

(1.1)

где R 2 = {(x, y) | x, y Î R} − множество всевозможных упорядоченных пар действительных чисел (рис. 1.1).

Рис. 1.1

Для того чтобы при построении теории функций, имеющих вид (1.1), прослеживалась аналогия с теорией

вещественнозначных функций вещественной переменной, необходимо, во-первых, ввести во множестве R 2 операции сложения и умножения элементов таким образом, чтобы это множество стало полем (известно [2.11, с. 146], что множество

R вещественных чисел является полем), и, во-вторых, элементы (x, y) поля R 2 (значения аргумента функции f )

рассматривать как новые числа.

Определение 1.1. Комплексным числом называется упорядоченная пара действительных чисел (обозначение: z = (x, y) ).

В силу определения 1.1 R 2 представляет собой множество всех комплексных чисел.
Определение 1.2. Два комплексных числа z1 = (x1, y1 ) , z2 = (x2 , y2 ) называются равными, если x1 = x2	и y1 = y2 .
Определение 1.3. Суммой комплексных чисел z1 = (x1, y1 ) и z2 = (x2 , y2 ) называется комплексное число вида
z1 + z2 = (x1 + x2 , y1 + y2 ) .	(1.2)

Операция сложения комплексных чисел обладает следующими свойствами [2.12, с. 99]:

1°. z1 + z2 = z2 + z1 , "z1, z2 Î R 2 (свойство коммутативности или переместительности операции сложения);

2°.

( z

+ z

2

) + z

= z + ( z

2

+ z

3

) ,

"z , z

2

, z

3

Î R 2

(свойство ассоциативности или сочетательности операции

1

3

1

1

сложения; в силу этого свойства допустима запись z1 + z2 + z3 );

3°.

z + 0 = z , "z Î R 2 , где 0 = (0,

0) (существование нулевого элемента);

4°.

z + (-z) = 0 ,

"z Î R 2 , где z =

(x, y), - z = (-x, -y) , 0 = (0, 0) (существование противоположного элемента).

Свойства 1° – 4° устанавливаются непосредственно, при этом используются соответствующие свойства операции

сложения действительных чисел [2.13, с. 29].
Определение 1.4. Произведением комплексных чисел z1 = (x1, y1 ) и z2	= (x2 , y2 ) называется комплексное число вида
z1z2	= (x1x2 - y1 y2 , x1 y2 + x2 y1 ) .	(1.3)

Операция умножения комплексных чисел обладает следующими свойствами [2.12, с. 99]:

5°. z1z2 = z2 z1 , "z1, z2 Î R 2 (свойство коммутативности или переместительности операции умножения);

6°.	( z z	2	) z	= z ( z	2	z	) , "z , z	2	, z	Î R 2 (свойство ассоциативности или сочетательности операции умножения; в
	1		3	1		3	1		3
силу этого свойства допустима запись z1z2 z3 );
7°.	z ×1 = z ,			"z Î R 2 , где 1 = (1,					0)	(существование единичного элемента);
8°.	"z Î R 2 , z ¹ (0, 0)						$ z−1 Î R		2 | z × z−1 = 1, где 1 = (1, 0) (существование обратного элемента).

Замечание 1.1. Непосредственно проверяется, что для комплексного числа z = (x, y) , z ¹ (0, 0) , обратным ему числом является комплексное число вида

x

y

z−1 =

, -

.

(1.4)

2

2

2

2

+ y

x

+ y

x

Выполнимость свойств 5° – 8° проверяется непосредственно.

В силу свойств 1° – 8°

множество

R 2 , наделённое операцией сложения (1.2) и операцией умножения (1.3), является

полем (определение поля см. в [2.11, с. 145]). Обозначим это поле символом C и назовём полем комплексных чисел.

Рассмотрим множество

комплексных чисел вида H = {(x, 0) | x Î R} . Между множеством

H

и множеством R

действительных чисел существует взаимно однозначное соответствие

(x, 0) « x, "x Î R .

(1.5)

Заметим, что в силу определений 1.3, 1.4 и соответствия (1.5) для любых (x1, 0) ,

(x2 , 0) Î H

(x1,0) + (x2 , 0) = (x1 + x2 , 0) « x1 + x2 ,

(x1, 0)(x2 , 0) = (x1x2 , 0) « x1x2 ,

т.е. комплексные числа из множества H складываются и перемножаются друг с другом так же, как соответствующие им

действительные числа. Следовательно,

любое комплексное число (x, 0) Î H можно отождествить с соответствующим ему

действительным числом x R :

(x, 0) = x, "x Î R ,

(1.6)

в частности, (0, 0) = 0, (1, 0) = 1 .

В силу (1.6) можно считать, что

R C , т.е. поле комплексных чисел является расширением поля действительных

чисел.

Любое комплексное число z = (x, y) можно представить в виде

z = (x, y) = (x, 0) + (0,1)( y, 0) .

(1.7)

Из (1.7) видно, что комплексное число (0,1) имеет особое значение в поле C . Это число принято обозначать символом

iи называть мнимой единицей. Заметим, что в силу (1.3), (1.6)

i2 = i ×i = (0,1)(0,1) = (-1, 0) = -1.

Всилу соглашения (1.6) формула (1.7) принимает вид

z = x + iy .	(1.8)
Выражение (1.8) называется алгебраической формой записи (представления) комплексного числа	z = (x, y) , при этом
число x называется действительной частью комплексного числа z и обозначается Re z (Re –	начальные буквы

французского слова reele – действительный), число y называется мнимой частью комплексного числа z			и обозначается
Im z (Im –	начальные буквы французского слова imagimaire – мнимый). Например, для комплексного числа z = 2 − 3i			имеем
Re z = 2 ,	Im z = −3 . Если y = Im z = 0 , то z = x является действительным числом. Если x = Re z = 0 и		y ¹ 0 , то	z = iy
(числа такого вида называются чисто мнимыми числами).
Условие равенства комплексных чисел, записанных в алгебраической форме, принимает вид
		x1 + iy1 = x2 + iy2 , если x1 = x2 и y1 = y2 ,		(1.9)
т.е. если Re z1 = Re z2		и Im z1 = Im z2 .
Замечание 1.2.		Понятия "больше" и "меньше" для комплексных чисел не определены (эти понятия сохраняют силу
лишь для комплексных чисел вида z = x , где x R ).
Правило (1.2) сложения комплексных чисел, записанных в алгебраической форме, принимает вид
		z1 + z2 = ( x1 + iy1 ) + ( x2 + iy2 ) = ( x1 + x2 ) + i ( y1 + y2 ) ,		(1.10)
т.е. при сложении комплексных чисел складываются отдельно их действительные части и отдельно их мнимые части.
Правило (1.3) умножения комплексных чисел, записанных в алгебраической форме, принимает вид
		z1z2 = ( x1 + iy1 )( x2 + iy2 ) = ( x1x2 - y1 y2 ) + i ( x1 y2 - x2 y1 ) .		(1.11)

Заметим, что правая часть формулы (1.11) получается, если в её левой части применить обычное алгебраическое правило умножения многочлена на многочлен (заменив при этом i2 на –1).

Операция вычитания комплексных чисел вводится как операция, обратная операции сложения: по определению, z1 - z2 = z3 | z2 + z3 = z1 . Следовательно,

z1 - z2 = ( x1 + iy1 ) - ( x2 + iy2 ) = ( x1 - x2 ) + i ( y1 - y2 ) ,

(1.12)

т.е. при вычитании комплексных чисел вычитаются отдельно их действительные части и отдельно их мнимые части.

Операция деления комплексных чисел вводится как операция, обратная операции умножения: по определению, если

z

2

¹ 0 , то

z1

= z

| z

2

z

= z . Следовательно, [2.12, с. 100],

3

3

1

z2

z1

=

x1 + iy1

=

x1x2 + y1 y2

+ i

x2 y1 - x1 y2

.

(1.13)

z

2

x + iy

2

x2

+ y2

x2

+ y2

2

2

2

2

2

Формула (1.13) громоздка, поэтому не обязательно её запоминать. Укажем простое правило, позволяющее находить

частное двух комплексных чисел.

Определение 1.5. Комплексное число

= x − iy называется комплексно сопряженным числу z = x + iy .

z

В силу (1.11)

z ×

= x2 + y2 ,

(1.14)

z

т.е. произведение комплексного числа z и комплексно сопряженного ему числа

равно сумме квадратов действительной и

z

мнимой частей числа z .

Используя формулу (1.14), деление комплексных чисел можно производить по следующему правилу: чтобы найти частное двух комплексных чисел, достаточно числитель и знаменатель дроби умножить на число, комплексно сопряженное знаменателю:

		z1			=	x1 + iy1								=	( x1 + iy1 )( x2 - iy2 )								=	x1x2 + y1 y2			+ i	x2 y1 - x1 y2				, (1.15)
		z	2			x				+ iy			2		( x	+ iy	2	)( x	2	- iy	2	)		x2	+ y	2		x	2	+ y	2
							2								2									2		2			2		2
т.е.
		z1		=		z1					2	.
								z
	z2					z	2			2
Пример 1.1. Пусть z1 = -3 + 2i , z2 = 4 - i . Тогда

z1 + z2 = (-3 + 4) + i (2 + (-1)) = 1+ i ;

z1 - z2 = (-3 - 4) + i (2 - (-1)) = -7 + 3i ;

z1z2 = (-3 + 2i )(4 - i) = -12 + 3i + 8i - 2i2 = -10 +11i ;

z

=

-3 + 2i

=

(-3 + 2i)(4 + i)

=

-12 - 3i + 8i + 2i2

= -

14

+ i ×

5

z2

4 - i

(4 - i )(4 + i )

42 + (-1)2

17

17 .

1

Непосредственной проверкой устанавливаются следующие соотношения:

z = z , z C ; z = z z R ;

для "z1, z2 Î C (в случае частного z2 ¹ 0 )

z1 + z2 = z1 + z2 ;

z1 - z2 = z1 - z2 ;

z1z2 = z1z2 ;

	z
					z
	1		=			1		.
z2					z2

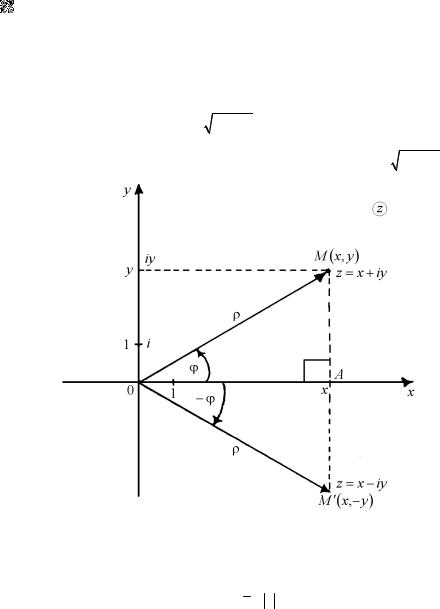
Пусть на плоскости задана декартова прямоугольная система координат xOy				(рис. 1.2). Тогда каждое комплексное
число z = (x, y) = x +iy	изображается на этой плоскости точкой М с абсциссой x			и ординатой	y или радиус-вектором
OM = {x, y} точки М.	Плоскость,	точки которой	отождествлены с комплексными числами,		называется	комплексной
плоскостью и обозначается тем		же символом	C , что и поле комплексных чисел; при этом ось Ox			называется

действительной осью (на ней изображаются действительные числа), ось Oy называется мнимой осью (на ней изображаются

чисто мнимые числа).

Тот факт, что данная плоскость рассматривается как

плоскость комплексного переменного z ,

отмечается значком

в первой четверти.

Определение 1.6.

Модулем комплексного числа

z = x +iy

называется расстояние от точки M = (x, y ) , изображающей

это число на комплексной плоскости, до начала

координат

O = (0, 0) (или,

другими словами, длина вектора

OM )

(обозначение:

z

или ρ ).

По определению,

z

³ 0 и

z

= 0 Û z = 0 .

UUUUUR

= x2 + y2

, следовательно,

Длина вектора OM выражается формулой

OM

r = x2 + y2 .

(1.16)

Рис. 1.2

В силу (1.16) формулу (1.14) можно записать в виде

z × z = z 2 .

Определение 1.7. Аргументом комплексного числа z = x +iy , z ¹ 0 , называется величина угла наклона вектора

OM = {x, y} , изображающего число z на комплексной плоскости, к положительному направлению действительной оси

(обозначение: Arg z ).

Величина такого угла имеет бесконечное множество значений, которое можно записать в виде

Arg z = arg z + 2pk, k Î Z ,

где arg z – значение аргумента числа z , выбранное из полуинтервала (-p, p](величина arg z определяется однозначно и

называется главным значением аргумента комплексного числа z ; в целях краткости будем также arg z обозначать через ϕ ).

Заметим, что комплексно сопряжённые числа z = x +iy и

= x −iy

изображаются на комплексной плоскости точками,

z

симметричными относительно действительной оси, следовательно,

=

z

, arg

= −arg z для "z Î C | z ¹ 0 , z Î R − , где

z

z

R − = {x Î R | x < 0} (рис. 1.2).

Замечание 1.3. Для комплексного числа z = 0 понятие аргумента не определено. Из прямоугольного DOAM (рис. 1.2) получаем