II. Функциональные последовательности и ряды

§1. Функциональная последовательность и функциональный ряд. Область сходимости

Пусть дана последовательность

(1)

все члены которой являются функциями, определенными на множестве . Возьмем(фиксированное число). Получим последовательностькоторая является числовой. Она может как сходиться, так и расходиться. Если последовательностьсходится (расходится), то последовательностьсходится (расходится) в точке.

Определение1. Множество всех точек области , в которых функциональная последовательностьсходится, называется областью сходимости последовательности .

Пусть последовательность (1) сходится на множестве . Тогда влюбой точке существует предел последовательности (1), то есть. Очевидно,- функция, определенная на. Она называется предельной функцией последовательности (1).

Обозначение: или.

Рассмотрим теперь ряд

, (2)

членами которого являются функции, определенные на множестве . Составим последовательность частичных сумм ряда (2), где

.

Последовательность - функциональная. Если она сходится нак предельной функции, то и ряд (2) сходится наи его сумма равна. Так как сходимость последовательностинаопределяется как сходимость в любой точкемножества, то и сходимость ряда (2) наопределяется как сходимость в любой точке. А именно, приряд (2) превращается в числовой ряд. Если он сходится, то функциональный ряд (2) сходится в точке.

Определение 2. Областью сходимости ряда (2) называется множество точек из области , в каждой из которых ряд (2) сходится.

Если ряд (2) сходится на некотором множестве Е, т.е. , то функцияS(x) называется суммой ряда (2): .

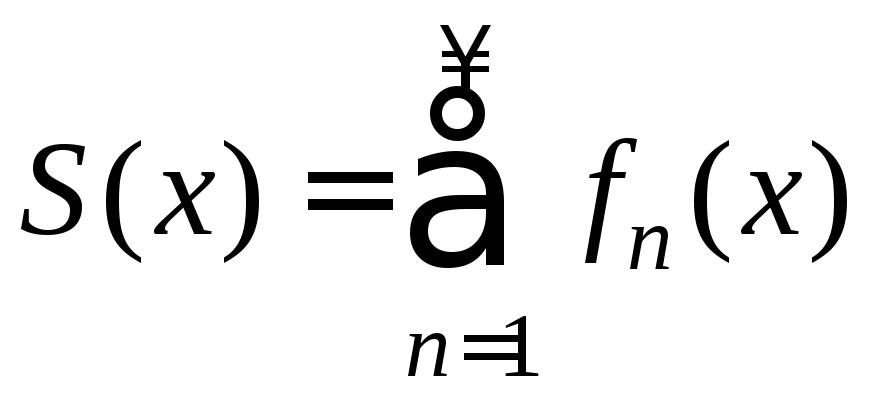Ряд (3) называетсяn–ым остатком ряда (2). Т.к. в любой точке множества Е ряд и любой из его остатков эквивалентны по сходимости, то если ряд (2) сходится на Е, то и любой из его остатков (3) сходится на Е. В этом случае, обозначим его сумму 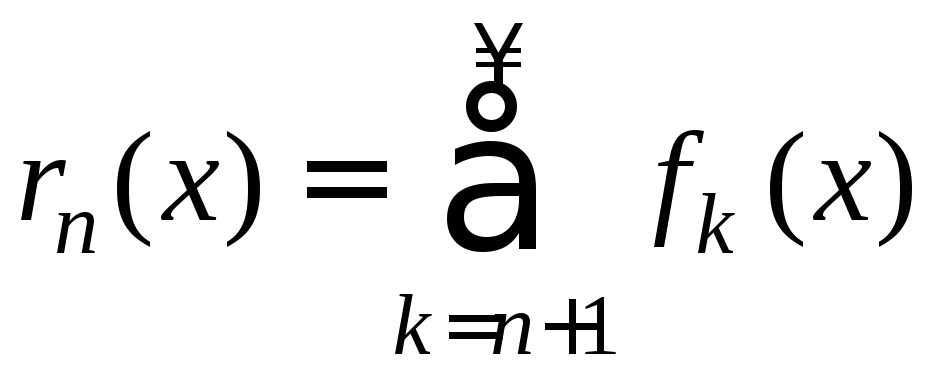, тогда.

Пример 1. Найти область сходимости последовательности :=xⁿ и её предельную функцию.

Δ

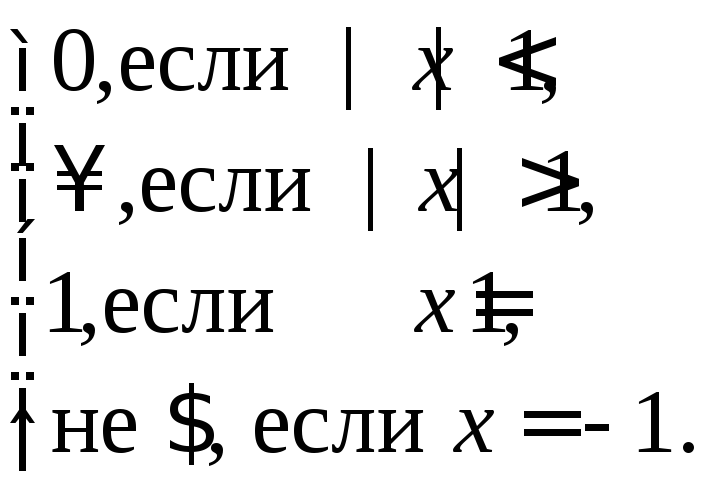
Следовательно, область сходимости х(-1;1].

S(x)=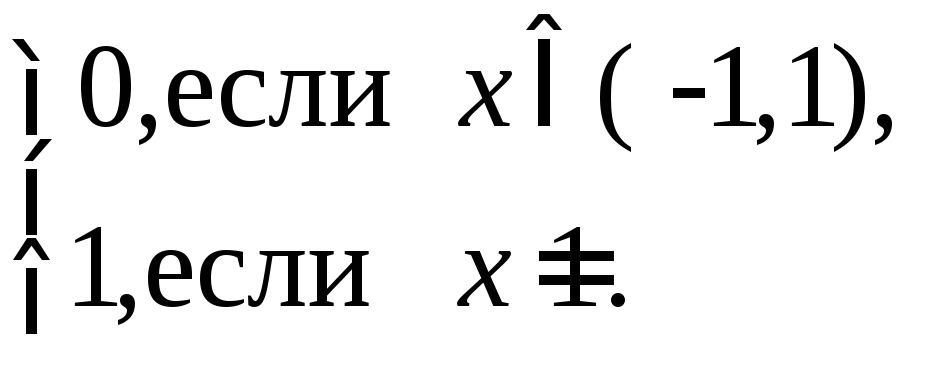Δ

Пример 2. Найти область сходимости и сумму ряда 1+x+…+x^n-1+…=.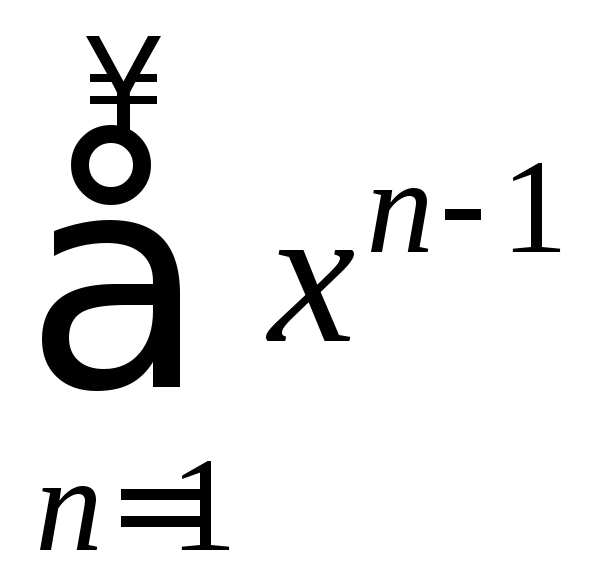

Δ Для произвольного ряд является геометрическим, следовательно, он сходится при |x|<1, и его сумма S(x)=. Δ

Пример 3. .

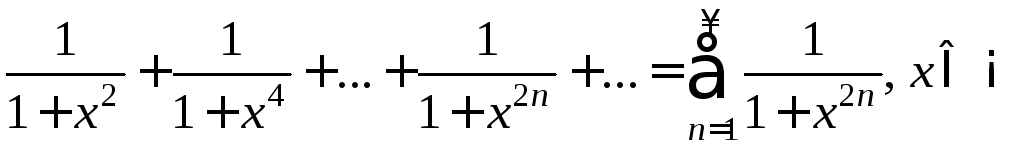Δ 1) |x|<1. Тогда ряд расходится.

2) |x|=1.. Ряд расходится.

3) |x|>1. В этом случае . Ряд является положительнымх из области |х|>1. Применим признак Даламбера

,

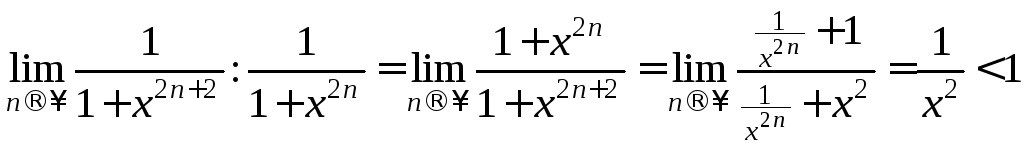значит, ряд сходится.

Ответ: область сходимости .Δ

§2. Равномерная сходимость функциональных последовательностей и рядов

1. Равномерная сходимость функциональной последовательности

Пусть функциональная последовательность сходится на множествеЕ к предельной функции S(x): . По определению предела это означает, что для любого фиксированного значенияпо любому заданному>0 найдется номер N, начиная с которого выполнено неравенство |S_n(x)-S(x)|<ε. Здесь под x понимается то значение, которое зафиксировано. В этом случае последовательность является числовой. Если взять другое значение х, то получится другая последовательность, и при том же ε номер N, начиная с которого выполняется неравенство |S_n(x)-S(x)|<ε будет, вообще говоря, другим. Т.к. х принимает бесконечное множество значений на Е, то получим бесконечное множество различных числовых последовательностей, сходящихся к пределу. Для каждой из них в отдельности существует свой номер N. Возникает вопрос: существует ли номер N, который при заданном ε был бы пригоден для всех этих последовательностей, т.е. хЕ?

Определение. Если последовательность имеет на множествеЕ предельную функцию S(x), и , существует такой, не зависящий отх номер N, что при любых неравенство |S_n(x)-S(x)|<ε выполнено одновременно для всех хЕ, то говорят, что последовательность сходится к функции S(x) равномерно на Е.

, если выполнено

. (1)

Геометрический смысл равенства сходимости

функциональной последовательности

Перепишем неравенство (1) в виде:

.

Оно означает, что графики всех членов последовательности, начиная с некого номера, целиком расположены в полосе шириной 2 между графиками функций ина множествеЕ.

Т.к. ε – произвольное положительное число, то полоса может быть сколь угодно узкой. Поэтому члены последовательности с достаточно большими номерами сколь угодно мало отличаются от S(x) на множестве Е.

_{Пример 1. Доказать, что последовательность 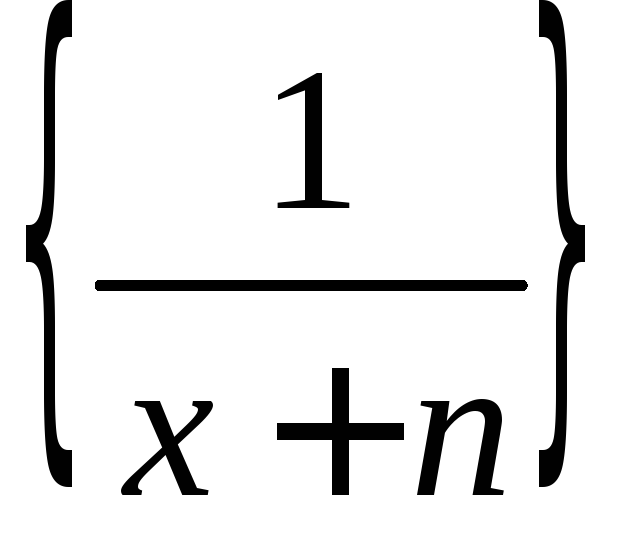равномерно сходится на отрезке [0;1] к S(x)=0.}

Δ Выберем произвольное ε>0. Найдем номер N, начиная с которого неравенство (1) будет выполнено для любых значений .

.

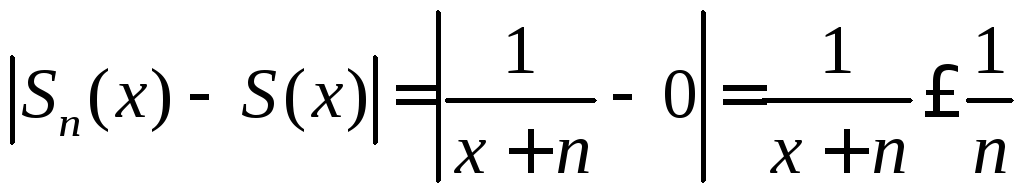
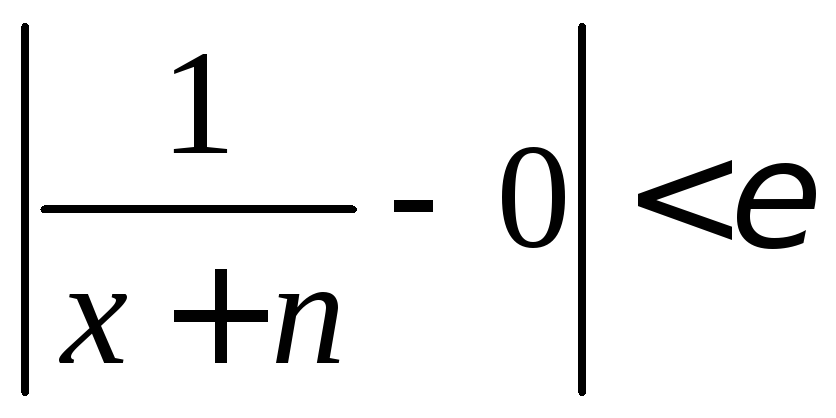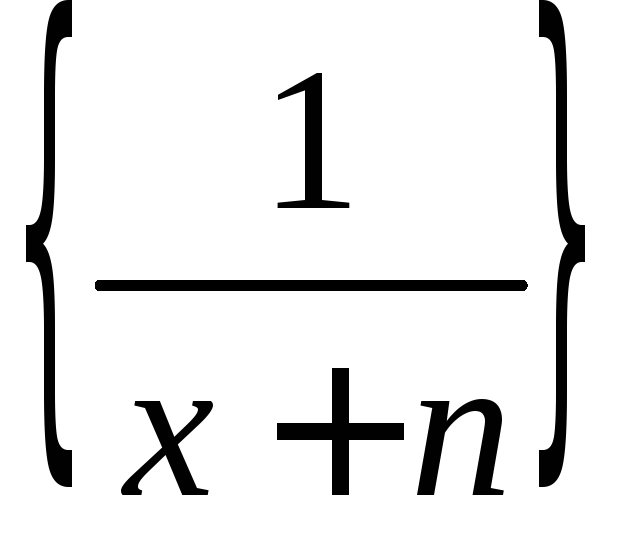Если потребовать, чтобы выполнялось , то требуемое неравенство будет выполнено. Отсюда. Возьмем. Итак, для выбранногоε , такой, чтоn>N и выполнено_. Значит, последовательность равномерно сходится на [0;1] кS(x)=0. Δ.